13.3: 地球表面附近的引力
- Page ID
- 204511
- 解释常量 G 和 g 之间的联系
- 通过天体表面的自由落体加速度确定其质量
- 描述 g 的值如何因位置和地球自转而变化
在本节中,我们将观察牛顿引力定律如何应用于行星表面,以及它如何与我们之前学到的关于自由落体的知识联系起来。 我们还研究了球形体内的引力效应。
重量
回想一下,地球表面附近自由落体物体的加速度约为 g = 9.80 m/s 2。 造成这种加速的力称为物体的重量,根据牛顿第二定律,它的值为 mg。 无论物体是否处于自由落体状态,此重量都存在。 我们现在知道这种力是物体和地球之间的引力。 如果我们用 mg 代替牛顿万有引力定律\(\vec{F}_{12}\)中的大小,m 代替 m 1,用 M E 代替 m 2,我们得到标量方程
\[mg = G \frac{m M_{E}}{r^{2}} \label{13.1}\]
其中 r 是物体质心和地球之间的距离。 地球的平均半径约为6370 km。 因此,对于距离地球表面几公里以内的物体,我们可以采取\(r = R_E\)(图\(\PageIndex{1}\))。 物体的质量 m 取消,离开
\[g = G \frac{M_{E}}{r^{2}} \ldotp \label{13.2}\]
这就解释了为什么所有质量都以相同的加速度自由落体。 我们忽略了这样一个事实,即地球也会向坠落的物体加速,但只要地球的质量比物体的质量大得多,这是可以接受的。
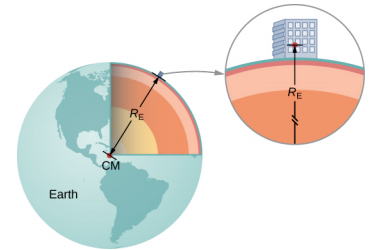
你有没有想过我们是怎么知道地球质量的? 我们当然不能把它放在比例上。 g 的值和地球半径是在几个世纪前以合理的精度测量的。
- 使用 g、R E 和方程\ ref {13.2} 的标准值来计算地球的质量。
- 估计 g 在月球上的值。 使用月球半径约为1700 km这一事实(该精度值是在许多世纪前确定的),并假设它的平均密度与地球相同,为5500 kg/m 3。
策略
有了 g 和 R E 的已知值,我们可以使用方程\ ref {13.2} 来找出 M E。 对于月球,我们使用平均密度相等的假设来根据地球和月球体积的比率来确定质量。
解决方案
- 重新排列方程\ ref {13.2},我们有 $$M_ {E} =\ frac {g R_ {E} ^ {2}} {G} =\ frac {(9.80\; m/s^ {2}) (6.37\ times 10^ {6}\; m) ^ {2}} {6.67\ times 10^ {-11}\; N\; ^ {2} /kg^ {2}} = 5.95\ times 10^ {24}\; kg\ ldotp$$
- 球体的体积与立方半径成正比,所以一个简单的比率给我们 $$\ frac {M_ {M}} {M_ {E}} =\ frac {R_ {M} ^ {3}} {R_ {E} ^ {3}}\ rightarrow M_ {M} =\ 左 (\ dfrac {(1.7\ times 10^ {6}\; m) ^ {3}} {(6.37\ times 10^ {6}\; m) ^ {3}}\ 右) (5.95\ times 10^ {24}\; kg) = 1.1\ times 10^ {23}\; kg\ ldotp$我们现在使用方程\ ref {13.2}。 $$g_ {M} = G\ frac {M_ {M}} {r_ {M} ^ {2}} = (6.67\ times 10^ {-11}\; N\;\ cdotp m^ {2} /kg^ {2})\ 左 (\ dfrac {1.1\ times 10^ {23}\; kg} {(1.7\ times 10^ {6}; m) ^ {2}}\ 右) = 2.5\; m/s^ {2} $$
意义
卡文迪什在1798年确定了G的值后,就可以计算出地球的质量。 (事实上,这首先是卡文迪许实验的最终目的。) 我们计算的月球 g 的值不正确。 月球的平均密度实际上仅为3340 kg/m 3,g = 1.6 m/s 2。 牛顿试图通过比较太阳对地球海潮的影响与月球的影响来测量月球的质量。 他的价值是两倍太小了。 g 和月球质量的最精确值来自于跟踪绕月球运行的航天器的运动。 但是月球的质量实际上可以在不去月球的情况下准确地确定。 地球和月球围绕一个共同的质心运行,仔细的天文测量可以确定该位置。 月球质量与地球的质量之比是 [从公共质心到月球中心的距离] 与 [从共同质心到地球中心的距离] 的比率。
在本节后面,我们将看到,其他天体的质量也可以由小型卫星绕它们运行的时间来确定。 但是在卡文迪什确定 G 的值之前,所有这些物体的质量都是未知的。
国际空间站在轨道上,距离地球表面 400 km 的值是多少?
解决方案
使用 M E 的值并注意半径为 r = R E + 400 km,我们使用方程\ ref {13.2} 来求出 g。根据方程\ ref {13.2} 我们有
\[g = G \frac{M_{E}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2}) \left(\dfrac{5.96 \times 10^{24}\; kg}{(6.37 \times 10^{6} + 400 \times 10^{3}\; m)^{2}}\right) = 8.67\; m/s^{2} \ldotp\]
意义
我们经常看到宇航员在空间站的视频,显然是失重的。 但很明显,重力正在作用在它们身上。 将我们刚刚计算的g值与地球上的g值(9.80 m/s 2)进行比较,我们发现国际空间站中的宇航员的体重仍为88%。 它们之所以显得失重,是因为它们处于自由落体状态。 我们将在《卫星轨道与能源》中回过头来讨论这个问题。
你在高层建筑顶部的重量与一楼的重量相比如何? 你认为工程师在为超高层建筑设计结构支撑时需要考虑g值的变化吗?
引力场
方程\ ref {13.2} 是一个标量方程,它给出引力加速度的大小与导致加速度的质心距离的函数。 但是我们本可以在方程\ ref {13.1} 中保留重力的向量形式,然后将加速度写成矢量形式
\[\vec{g} = G \frac{M}{r^{2}} \hat{r} \ldotp\]
我们将由质量引起的引力场识别\(\vec{g}\)为由质量 M 引起的引力场。我们可以将该场描绘成如图所示\(\PageIndex{2}\)。 这些线向径向内指向,围绕质量对称分布。
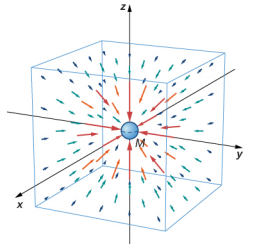
与任何矢量场一样,在任何点的方向\(\vec{g}\)都平行于场线。 任何\(\vec{g}\)点的强度与线间距成反比。 另一种说法是,任何区域中场的大小与穿过单位表面积的线条数成正比,实际上是线的密度。 由于直线在所有方向上的间距相等,因此距离质量 r 处每单位表面积的线数等于线总数除以半径为 r 的球体的表面积,后者与 r 2 成正比。 因此,这张照片除了表示场的方向外,还完美地代表了反平方定律。 在场图中,我们说质量 m 与质量 M 的引力场相互作用。我们将在后面关于电磁学的章节中充分利用场的概念。
表观重量:考虑地球自转
正如我们在《牛顿定律的应用》中所看到的那样,以恒定速度移动的物体具有指向圆心的向心加速度,这意味着必须有净力指向该圆的中心。 由于地球表面的所有物体每 24 小时穿过一个圆圈,因此每个物体上必须有指向该圆心的净向心力。
让我们首先考虑一个质量为 m 的物体,位于赤道上,悬挂在比例上(图\(\PageIndex{3}\))。 刻度在\(\vec{F}_{s}\)远离地球中心的地方施加向上的力。 这是体重秤上的读数,因此它是物体的表观重量。 重量(mg)指向地球中心。 如果地球不旋转,则加速度将为零,因此,净力将为零,导致 F s = mg。 这将是体重的真实读数。
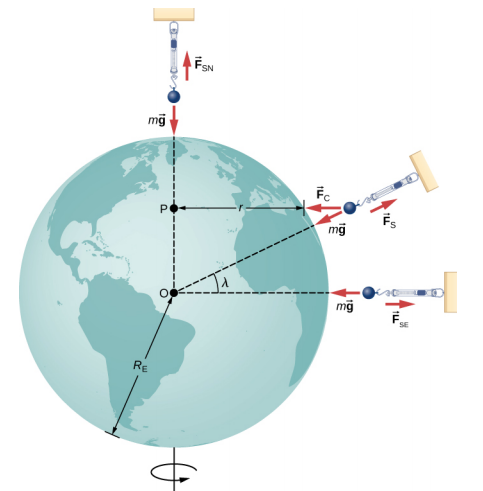
在旋转时,这些力的总和必须提供向心加速度\(a_c\)。 使用牛顿第二定律,我们有
\[\sum F = F_{s} - mg = ma_{c} \quad where\; a_{c} = - \frac{v^{2}}{r} \ldotp \label{13.3}\]
请注意,a c 指向的方向与权重相同;因此,它是负数。 切线速度 v 是赤道上的速度,r 是 R E。 我们可以通过注意赤道上的物体在 24 小时内沿地球的周长行驶来计算速度。 取而代之的是,让我们使用二维和三维运动中的 c 的替代表达式。 回想一下,切向速度与角速度 (\(\omega\)) 有关 v = r\(\omega\)。 因此,我们有 c = −r\(\omega\) 2。 通过重新排列方程 13.3 并用 r = R E 代替,赤道的表观重量为
\[F_{s} = m (g - R_{E} \omega^{2}) \ldotp\]
各地地球的角速度是
\[\omega = \frac{2 \pi\; rad}{24\; hr \times 3600\; s/hr} = 7.27 \times 10^{-5}\; rad/s \ldotp\]
用 R E 和的值代替 R E 2\(\omega\),我们得出 R E\(\omega\) 2 = 0.0337 m/s 2。 这仅为重力值的0.34%,因此显然是一个很小的修正。
地球需要多快旋转才能使赤道上的人的表观重量为零? 一天会持续多久?
策略
使用方程\ ref {13.3},我们可以将视在权重 (F s) 设置为零并确定所需的向心加速度。 由此,我们可以找到赤道的速度。 一天的长度是完成一次轮换所需的时间。
解决方案
根据方程\ ref {13.2},我们有\(\sum\) F = F s − mg = ma c,所以设置 F s = 0,我们得到 g = a c。 使用 a c 的表达式,代替地球的半径和重力的标准值,我们得到
\[\begin{split} a_{c} & = \frac{v^{2}}{r} = g \\ v & = \sqrt{gr} = \sqrt{(9.80\; m/s^{2})(6.37 \times 10^{6}\; m)} = 7.91 \times 10^{3}\; m/s \ldotp \end{split}\]
周期 T 是完成一次旋转的时间。 因此,切向速度等于周长除以 T,所以我们有
\[\begin{split} v & = \frac{2 \pi r}{T} \\ T & = \frac{2 \pi r}{v} = \frac{2 \pi (6.37 \times 10^{6}\; m)}{7.91 \times 10^{3}\; m/s} = 5.06 \times 10^{3}\; s \ldotp \end{split}\]
这大约是 84 分钟。
意义
我们将在本节后面看到,这个速度和一天的长度也将是卫星在地球表面轨道上的轨道速度和周期。 尽管由于空气阻力,在地球表面附近不可能有这样的轨道,但肯定只有在距离地球几百英里的地方才有可能。
结果远离赤道
在两极处,a c → 0 和 Fs = mg,就像没有旋转的情况一样。 在任何其他领域\(\lambda\),情况都更加复杂。 向心加速度指向图中的点 P,半径变为\(r = R_E \cos \lambda\)。 权重的矢量总和,\(\vec{F}_{s}\)必须指向点 P,因此\(\vec{F}_{s}\)不再指向远离地球中心。 (图中差异很小而且夸大了。) 铅锤总是指向这个偏离的方向。 所有建筑物都是沿着这个偏离的方向对齐建造的,而不是沿着穿过地球中心的半径建造的。 对于最高的建筑物来说,这表示顶部有几英尺的偏差。
还值得注意的是,地球不是一个完美的球体。 内部部分是液态的,这增强了赤道旋转导致的地球膨胀。 与两极相比,赤道处的地球半径大约大30千米。 使用方程式\ ref {13.2} 比较两极的重力与赤道的重力只能作为练习。 差异与旋转产生的差异相当,方向相同。 显然,你真的可以通过搬到热带来减肥。
重力远离地面
之前我们在没有证据的情况下指出,引力定律适用于球形对称的物体,其中每个物体的质量就好像它在身体的中心一样起作用。 由于方程\ ref {13.2} 源自方程\ ref {13.1},因此它也适用于对称质量分布,但两个方程仅对值有效\(r ≥ R_E\)。 正如我们在示例 13.4 中所见,在距离地球表面 400 千米处,即国际空间站运行的地方,值\(g\)为 8.67 m/s 2。 (稍后我们将看到,这也是国际空间站的向心加速度。)
因为\(r < R_E\),方程\ ref {13.1} 和方程\ ref {13.2} 无效。 但是,我们可以使用来自高斯定律的原理来确定这些案例的 g,高斯定律是一种强大的数学工具,我们将在本课程的后面进行更详细的研究。 应用于引力的高斯定律的一个结果是,只有 r 内的质量才会产生引力。 此外,与以前一样,该质量可以被认为位于中心。 r 外质量的引力效应净效应为零。
出现了两个非常有趣的特殊情况。 对于密度恒定的球形行星,r 内的质量是密度乘以 r 内的体积。可以认为该质量位于中心。 将 M E 替换为仅在 r 内的质量,M =\(\rho\) x(球体的体积),将 R E 替换为 r,方程\ ref {13.2} 变成
\[g = G \frac{M_{E}}{R_{E}^{2}} = G \frac{\rho \left(\dfrac{4}{3} \pi r^{3}\right)}{r^{2}} = \frac{4}{3} G \rho \pi r \ldotp\]
当你从洞里下降到球形行星的中心时,g 的值以及你的体重会线性降低。 在中心,你失重,因为行星的质量在各个方向上均匀移动。 实际上,地球的密度不是恒定的,整个地球也不是固体的。 该图\(\PageIndex{4}\)显示了地球密度\(g\)是否恒定的剖面图,以及根据地震数据得出的密度估计得出的更可能的剖面图。
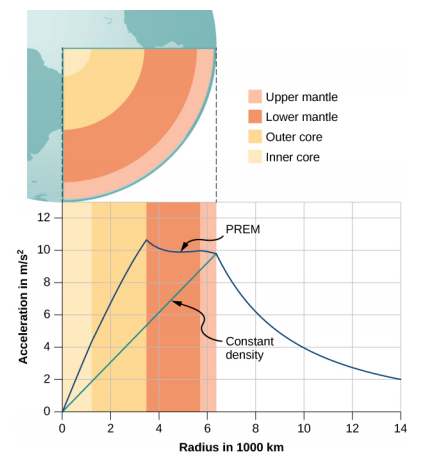
第二个有趣的案例涉及生活在球壳行星上。 许多科幻小说中都提出了这种情景。 忽略重大的工程问题,炮弹可以按所需的半径和总质量建造,这样地表的 g 与地球的重量相同。你能猜出一旦你乘坐电梯下降到炮弹内部,你和中心之间没有质量,会发生什么吗? 这对于从球体上的一个点到另一个点的长距离行驶会带来什么好处? 最后,如果行星在旋转,会产生什么影响?


