13.2: 牛顿万有引力定律
- Page ID
- 204510
- 列出引力历史上的重要里程碑
- 计算两个点质量之间的引力
- 估计质量集合之间的引力
我们首先回顾一下引力研究的历史,重点是几千年来激发哲学家和科学家寻找解释的那些现象。 然后我们研究牛顿万有引力定律的最简单形式以及如何应用它。
引力的历史
最早的哲学家想知道为什么物体自然会掉落到地面。 亚里士多德(公元前 384—322 年)认为,寻找地球是岩石的本质,寻找天堂是火的本质。 Brahmagupta(公元 598~665 年)假设地球是一个球体,物体对它具有天生的亲和力,无论它们位于何处,都向中心坠落。
太阳、月亮和行星的运动也被研究了数千年。 托勒密(公元 90—168 年)以惊人的精确度描述了这些运动,他的周周期方法将行星的路径描述为圆圈内的圆圈。 但是,直到十七世纪,几乎没有证据表明有人将天体的运动与落入地球的物体的运动联系起来。
尼古拉斯·哥白尼(1473—1543 年)被普遍认为是第一个挑战托勒密地心(以地球为中心)系统并提出以太阳系中心为中心的日心系统的人。 第谷·布拉赫对行星运动进行的极其精确的肉眼测量以及约翰内斯·开普勒和伽利略伽利略的分析都支持了这一想法。 开普勒证明每颗行星的运动都是一个椭圆(他的三个定律中的第一个,在开普勒的《行星运动定律》中进行了讨论),而罗伯特·胡克(制定胡克弹簧定律的同一个胡克)直观地暗示这些运动是由于行星被行星吸引太阳。 但是,正是艾萨克·牛顿将地球表面附近物体的加速度与月球在绕地球轨道上的向心加速度联系起来。
最后,在爱因斯坦的《引力理论》中,我们来看看阿尔伯特·爱因斯坦在1916年提出的广义相对论。 他的理论来自一个截然不同的视角,在这个视角中,重力是质量扭曲空间和时间的表现。 他的理论的后果引发了许多引人注目的预测,基本上所有这些预测在该理论发表后的几十年中都得到了证实(包括2015年对两个黑洞合并产生的引力波的测量)。
牛顿万有引力定律
牛顿指出,地球表面(因此距离地球中心 R E 的距离)的物体的加速度为 g,但是距离大约 60 R E 的月球向心加速度比 g 小约(60)倍。他可以通过假设来解释这一点任何两个物体之间都存在力,其大小由两个质量的乘积除以它们之间距离的平方得出。 我们现在知道这个反平方定律在自然界中无处不在,它是点源几何的函数。 距离 r 处任何源的强度分布在以质量为中心的球体表面上。 该球体的表面积与 r 2 成正比。 在后面的章节中,我们在电磁力中看到了同样的形式。
牛顿引力定律可以表示为
\[\vec{F}_{12} = G \frac{m_{1} m_{2}}{r^{2}} \hat{r}_{12} \label{13.1}\]
其中\(\vec{F}_{12}\)是物体 2 对对象 1 施加的力,\(\hat{r}_{12}\)是从物体 1 指向对象 2 的单位向量。
如图所示\(\PageIndex{1}\),向\(\vec{F}_{12}\)量从物体 1 指向对象 2,因此代表物体之间的吸引力。 相等但相反的力\(\vec{F}_{21}\)是物体 1 对物体 2 施加的力。
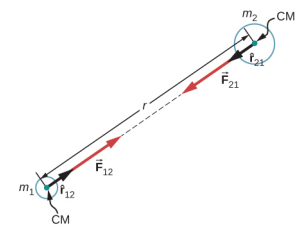
这些相等但相反的力反映了我们前面讨论过的牛顿第三定律。 请注意,严格来说,方程\ ref {13.1} 适用于点质量——所有质量都位于一个点。 但它同样适用于任何球形对称的物体,其中 r 是这些物体的质心之间的距离。 在许多情况下,如果非对称物体的间隔与它们的大小相比很大,并且我们把 r 作为每个物体质心之间的距离,那么它对于非对称物体的效果相当不错。
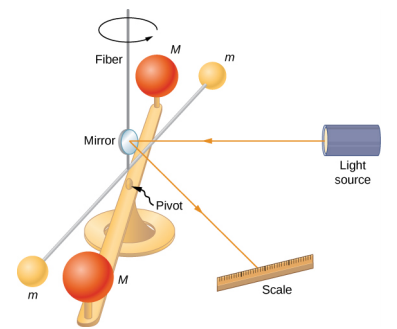
卡文迪许实验
牛顿发表万有引力定律一个世纪后,亨利·卡文迪什通过艰苦的实验确定了比例常数 G。 他制造了一种与图中所示的设备相似的装置\(\PageIndex{2}\),其中小块物悬挂在电线上。 一旦处于平衡状态,两个固定的较大质量就会对称地放置在较小的质量附近。 引力吸引力在支撑线上产生扭转(扭曲),可以测量。
常数 G 被称为通用引力常数,卡文迪许将其确定为 G = 6.67 x 10 −11 N • m 2 /kg 2。 “普遍” 一词表示科学家认为这个常数适用于任何成分的质量,并且在整个宇宙中都是相同的。 G 的值非常小,表明重力非常弱。 像我们的身体这样小的群体,甚至是摩天大楼大小的物体之间的吸引力非常小。 例如,相距 1.0 米的两个 1.0 千克的质量相互施加 6.7 x 10 −11 N 的力。 这是一粒典型花粉的重量。
尽管重力是自然界四种基本力量中最弱的一种,但它的吸引力是将我们带到地球,使行星绕太阳运行,太阳绕我们的银河系运行,并将星系绑定成从几到数百万的星团。 重力是构成宇宙的力量。
要确定由重力引起的运动,请执行以下步骤:
- 找出你想要找到引力的两个质量,一个或两个质量。
- 绘制自由体图,绘制作用于每个质量的力并指出其质心之间的距离。
- 将牛顿第二运动定律应用于每个质量以确定其移动方式。
以两个近似球形的联盟号有效载荷飞行器为例,它们在环绕地球的轨道上,每个重量为9000千克,直径为4.0米。它们最初相对于彼此处于静止状态,从中心到中心10.0米。 (正如我们将在开普勒的《行星运动定律》中看到的那样,两者都以相同的速度绕地球运行,相互作用几乎与它们被隔离在深空中一样。) 确定它们之间的引力及其初始加速度。 估计它们一起漂移需要多长时间,以及它们在撞击时移动的速度。
策略
我们使用牛顿引力定律来确定它们之间的力,然后使用牛顿第二定律找出每个定律的加速度。 对于估计值,我们假设该加速度是恒定的,我们使用沿直线运动得出的恒定加速度方程来计算碰撞的时间和速度。
解决方案
力的大小是
\[|\vec{F}_{12}| = F_{12} = G \frac{m_{1} m_{2}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2}) \frac{(9000\; kg)(9000\; kg)}{(10\; m)^{2}} = 5.4 \times 10^{-5}\; N \ldotp\]
每个有效载荷的初始加速度为
\[a = \frac{F}{m} = \frac{5.4 \times 10^{-5}\; N}{9000\; kg} = 6.0 \times 10^{-9}\; m/s^{2} \ldotp\]
车辆的直径为 4.0 米,因此车辆的距离从 10.0 米移动到 4.0 米,或者每辆车的距离为 3.0 米。 与上述计算方法类似,当车辆相距 4.0 m 时,得出的加速度为 3.8 x 10 −8 m/s 2,这两个值的平均值为 2.2 x 10 −8 m /s 2。 如果我们假设这个值的加速度是恒定的,并且它们从静止状态开始,那么车辆会以给出的速度碰撞
\[v^{2} = v_{0}^{2} + 2a (x - x_{0}),\; where\; v_{0} = 0,\]
所以
\[v = \sqrt{2(2.2 \times 10^{-9}\; N)(3.0\; m)} = 3.6 \times 10^{-4}\; m/s \ldotp\]
我们使用 v = v 0 + at 来查找 t = v/a = 1.7 x 10 4 秒或大约 4.6 小时。
意义
这些计算(包括初始力)只是估计值,因为车辆可能不是球形对称的。 但是你可以看到,力量非常小。 宇航员即使在大型国际空间站(ISS)外工作时也必须系好自己,如图所示\(\PageIndex{3}\),因为即使是最小的推离空间站,引力也无法使他们免受空间站最小的推动。

当车辆坠落在一起时,力和加速会发生什么? 我们对高于或低于实际速度的碰撞速度的估计值是多少? 最后,如果群众不完全一样会发生什么? 每个人的力量是相同还是不同? 他们的加速怎么样?
- 回答
-
在此处添加文本。 请勿先删除此文本。
两个具有质量的物体之间的重力对这些航天器顺序的影响确实很小。 然而,重力从地球上对你的影响非常严重,以至于只有几英尺的距离坠入地球可能很危险。 在下一节中,我们将研究地球表面附近的重力。
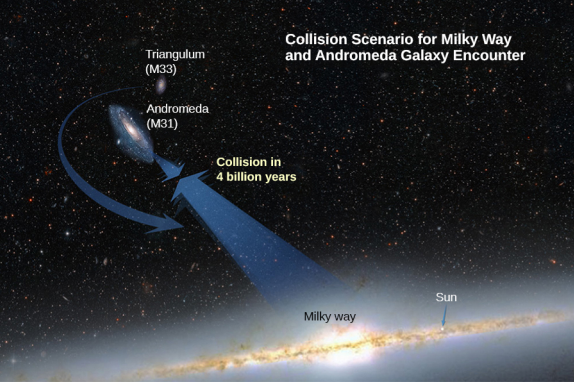
找出我们的银河系银河系的加速度,这是因为最接近的同等大小的星系仙女座星系(图\(\PageIndex{4}\))。 每个星系的大致质量为8000亿个太阳质量(太阳质量是我们太阳的质量),它们之间相隔250万光年。 (请注意,仙女座的质量并不为人所知,但据信它比我们的银河系略大。) 每个星系的直径约为 100,000 光年(1 光年 = 9.5 x 10 15 m)。

策略
与前面的示例一样,我们使用牛顿引力定律来确定它们之间的力,然后使用牛顿第二定律来找到银河系的加速度。 我们可以将星系视为点质量,因为它们的大小比它们的间隔小约25倍。 太阳的质量(见附录D)为2.0 x 10 30 kg,光年是光在一年内传播的距离,9.5 x 10 15 m。
解决方案
力的大小是
\[F_{12} = G \frac{m_{1} m_{2}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2}) \frac{[(800 \times 10^{9})(2.0 \times 10^{30}\; kg)]^{2}}{[(2.5 \times 10^{6})(9.5 \times 10^{15}\; m)]^{2}} = 3.0 \times 10^{29}\; N \ldotp\]
银河系的加速是
\[a = \frac{F}{m} = \frac{3.0 \times 10^{29}\; N}{(800 \times 10^{9})(2.0 \times 10^{30}\; kg)} = 1.9 \times 10^{-13}\; m/s^{2} \ldotp\]
意义
这个加速度值看起来小得惊人吗? 如果它们从静止开始,那么它们会直接向对方加速,在质心 “碰撞”。 让我们估计一下发生这种情况的时间。 初始加速度约为 10 −13 m/s 2,因此使用 v = at,我们可以看出,每个星系需要大约 10 13 秒才能达到 1.0 m/s 的速度,而距离它们只差大约 0.5 x 10 13 m。 这比它们之间的初始距离小九个数量级。 实际上,这样的动作很少是简单的。 这两个星系以及其他大约 50 个较小的星系都被引力绑定到我们的局部星团中。 我们的局部星团在引力上与所谓的超级星团中的其他星团绑定。 所有这些都是由引力产生的伟大宇宙舞的一部分,如图所示\(\PageIndex{5}\)。