Skip to main content
Global

11.E：角动量（练习）

  1. Last updated
  2. Save as PDF
  • Page ID
    204394

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    概念性问题

    11.1 滚动动作

    1. 在无摩擦斜坡顶部从静止状态中释放的圆形物体能否进行滚动运动？
    2. 半径为 R 的圆柱形罐头在水平表面上滚动而不会滑动。 (a) 罐头旋转一圈后，其质心移动的距离是多少？ (b) 如果发生滑动，这个距离会更大还是更小？
    3. 车轮在斜坡上从顶部松开。 如果斜坡较陡或稍微倾斜，车轮最有可能滑动吗？
    4. 哪个更快地向下滚动倾斜平面，是空心圆柱体还是实心球？ 两者的质量和半径相同。
    5. 具有相同半径和质量的空心球体和空心圆柱体在斜坡上滚动而不会滑动，并且具有相同的初始质心速度。 哪个物体在停止之前达到了更高的高度？

    11.2 角动量

    1. 你能否在不事先定义参考点的情况下为粒子分配角动量？
    2. 对于直线传播的粒子，有没有角动量为零的点？ 假设这条线与原点相交。
    3. 在什么条件下，刚体有角动量但没有线性动量？
    4. 如果粒子相对于所选原点移动，则它具有线性动量。 必须存在什么条件才能使该粒子相对于所选原点的角动量为零？
    5. 如果你知道粒子的速度，你能谈谈粒子的角动量吗？

    11.3 角动量守恒

    1. 直升机后部的小型螺旋桨在飞机上垂直于大型螺旋桨旋转，其目的是什么？
    2. 假设一个孩子从旋转旋转木马的外缘走到里面。 旋转木马的角速度是增加、减少还是保持不变？ 解释你的答案。 假设旋转木马在没有摩擦的情况下旋转。
    3. 当系留球的绳子绕着杆子缠绕时，球的角速度会怎样？
    4. 假设极地冰盖破裂并在没有融化的情况下向地球赤道漂浮。 地球的角速度会怎样？
    5. 解释为什么星星在倒塌时旋转得更快。
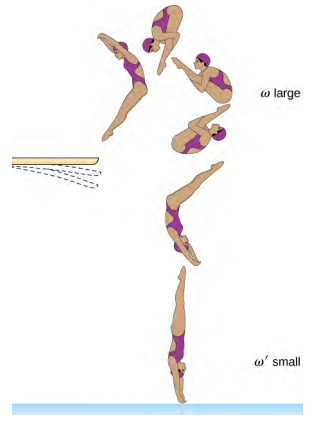
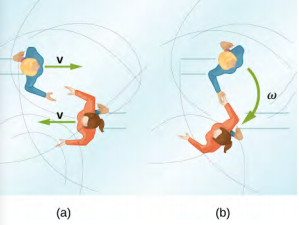
    6. 竞技潜水员在翻转时会伸出四肢然后 curl 缩身体。 就在进入水中之前，他们完全伸出四肢直接向下进入（见下文）。 解释这两个动作对其角速度的影响。 还要解释对它们角动量的影响。

    一幅潜水员在潜水中多个时刻的画作，从刚离开跳水板到进入水中之前。 离开棋盘后，潜水员处于长矛姿势，双腿靠近身体，欧米茄很大。 当她靠近水面时，她会伸展身体。 她到达水面时完全伸展且垂直，而 omega prime 很小。

    11.4 陀螺仪的进动

    1. 制导系统中用于指示太空方向的陀螺仪必须具有不会改变方向的角动量。 当放置在车辆中时，它们被放置在与主机身分开的隔间中，这样机身方向的变化就不会影响陀螺仪的方向。 如果太空飞行器受到很大的力和加速度，陀螺仪角动量的方向怎么能始终保持恒定？
    2. 地球绕其垂直轴移动，周期为26,000年。 讨论是否可以使用方程 11.12 来计算地球的进动角速度。

    问题

    11.1 滚动动作

    1. 在 90.0 km/h 行驶的汽车上，直径为 75.0 cm 的轮胎的角速度是多少？
    2. 一个男孩骑着自行车 2.00 公里。 车轮的半径为 30.0 厘米。 轮胎在旅途中旋转的总角度是多少？
    3. 如果前面问题中骑自行车的男孩在 10.0 秒内从静止状态加速到 10.0 m/s 的速度，那么轮胎的角加速度是多少？
    4. 一级方程式赛车的轮胎直径为66厘米。 如果一级方程式赛车在一场比赛中平均时速为300 km/h，那么如果赛车保持这个速度1.5小时，车轮的角位移是多少？
    5. 大理石从静止处以 30° 的角度向下滚动。 (a) 它的加速度是多少？ (b) 它在 3.0 秒内能走多远？
    6. 重复前面的问题，用实心圆柱替换大理石。 解释新结果。
    7. 横截面为圆柱形的刚性主体从 30° 斜度的顶部松开。 它在 2.60 秒内向底部滚动 10.0 m。根据物体的质量 m 和半径 r 求出物体的惯性矩。
    8. 可以认为溜溜球是一个质量为 m 和半径为 r 的实心圆柱体，其周长上缠绕着一根灯串（见下文）。 字符串的一端固定在空间中。 如果气缸在绳子松开时掉落而没有滑动，那么气缸的加速度是多少？

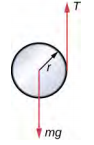
    圆柱体、半径 r 及其上的力的示意图。 力 m g 作用于圆柱体的中心并指向下方。 力 T 作用于右边缘，指向上方。

    1. 半径为 10.0 cm 的实心圆柱体在滑动时沿斜坡向下滚动。 倾斜角度为 30°。 表面的动摩擦系数为 0.400。 实心圆柱体的角加速度是多少？ 什么是线性加速度？
    2. 保龄球在坡道上滚动 0.5 m 高，不会滑到储藏处。 它的质心初始速度为 3.0 m/s。(a) 它在坡道顶部的速度是多少？ (b) 如果坡道高 1 米，它会到达山顶吗？
    3. 一个 40.0 千克的实心圆柱体以 6.0 m/s 的速度在水平表面上滚动。要停止它需要多少工作？
    4. 一个 40.0 千克的固体球体以 6.0 m/s 的速度在水平表面上滚动。要阻止它需要多少工作？ 将结果与前面的问题进行比较。
    5. 实心圆柱以 20° 的角度向上滚动斜面。 如果它以10 m/s的速度从底部开始，它会向上移动多远？
    6. 质量为 M 且半径为 R 的实心圆柱轮受\(\vec{F}\)施加到车轮中心的力向水平方向移动（见下图）。 如果车轮要在不打滑的情况下滚动，最大值是\(|\vec{F}|\)多少？ 静摩擦和动摩擦系数为\(\mu_{S}\) = 0.40 和\(\mu_{k}\) = 0.30。

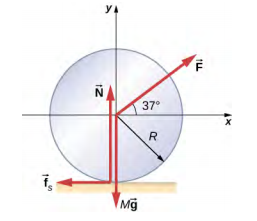
    显示了水平曲面上轮子（半径为 R）上的力。 轮子以 x y 坐标系为中心，该坐标系向右为正 x，正向上 y。 力 F 作用于车轮中心，角度比正 x 方向高 37 度。 力 M g 作用于车轮中心并指向下方。 力 N 指向上方并作用于车轮接触表面的接触点。 Force f sub s 指向左侧并作用于轮子接触表面的接触点。

    1. 滚动而不滑动的空心圆柱体的速度为 5.0 m/s，然后向上滚动倾斜到 1.0 m 的垂直高度。如果给定质量和半径相同的空心球体具有相同的初始速度，那么它在垂直方向上滚动的水平有多高？

    11.2 角动量

    1. 一个 0.2 千克的粒子以 5.0 m/s 的速度沿线 y = 2.0 m 移动。粒子围绕原点的角动量是多少？
    2. 一只鸟从你站立的地方飞过头顶，海拔 300.0 m，与地面的水平速度为 20.0 m/s。这只鸟的质量为 2.0 kg。 鸟的半径向量\(\theta\)与地面形成一个角度。 鸟的半径向量及其动量矢量位于 xy 平面中。 关于你所站立的位置，这只鸟的角动量是多少？
    3. 一辆重量为750.0 kg的一级方程式赛车正在摩纳哥的一条赛道上超速行驶，并以220.0 km/h的速度绕圈起点逆时针方向进入圆形转弯。 在赛道的另一部分，赛车也以逆时针方向以 180 km/h 的速度进入第二个环形转弯。 如果第一回合的曲率半径为 130.0 m，第二回合的曲率半径为 100.0 m，则比较每回合中围绕圆形转弯原点拍摄的赛车的角力矩。
    4. 质量为 5.0 kg 的粒子在特定时刻的位置向量\(\vec{r}\) = (2.0\(\hat{i}\) − 3.0\(\hat{j}\)) m，当其相对于原点的速度为\(\vec{v}\) = (3.0\(\hat{i}\)) m/s 时。 (a) 粒子的角动量是多少？ (b) 如果此时力\(\vec{F}\) = 5.0\(\hat{j}\) N 作用于粒子，则原点的扭矩是多少？
    5. 使用右手法则确定角力矩围绕粒子原点的方向，如下所示。 z 轴不在页面中。

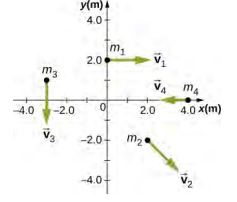
    显示了 x y 平面中具有不同位置和速度向量的四个粒子。 x 和 y 轴以米为单位显示位置，范围为 -4.0 到 4.0 米。 粒子 1 的质量 m sub 1，位于 x=0 米和 y=2.0 米，v sub 1 指向正 x 方向。 粒子 2 的质量 m sub 2，位于 x=2.0 米和 y=-2.0 米，v sub 2 指向右和向下，比正 x 方向低大约 45 度。 粒子 3 的质量 m sub 3，位于 x=-3.0 米和 y=1.0 米，v sub 3 指向负 y 方向。 粒子 4 的质量 m sub 4，位于 x=4.0 米和 y=0 米，v sub 4 指向左，朝负 x 方向。

    1. 假设前面问题中的粒子的质量为 m 1 = 0.10 kg，m 2 = 0.20 kg，m 3 = 0.30 kg，m 4 = 0.40 kg。 粒子的速度为 v 1 = 2.0\(\hat{i}\) m/s，v 2 = (3.0\(\hat{i}\) − 3.0\(\hat{j}\)) m/s，v 3 = −1.5\(\hat{j}\) m/s，v 4 = −4.0\(\hat{i}\) m/s。(a) 计算每个粒子围绕原点的角动量。 (b) 四粒子系统关于原点的总角动量是多少？
    2. 两个质量相等的粒子以相同的速度沿着由距离 d 隔开的平行线在相反的方向上移动。表明无论使用哪个点作为计算角动量的参考点，这个双粒子系统的角动量都是相同的。
    3. 质量为4.0 x 10 4 kg的飞机在10千米的高度水平飞行，相对于地球的恒定速度为250 m/s。 (a) 相对于飞机正下方的地面观察器，飞机的角动量是多少？ (b) 飞机沿其路径飞行时，角动量会发生变化吗？
    4. 在特定时刻，1.0 千克粒子的位置为\(\vec{r}\) = (2.0\(\hat{i}\) − 4.0\(\hat{j}\) + 6.0\(\hat{k}\)) m，其速度为\(\vec{v}\) = (−1.0\(\hat{i}\) + 4.0\(\hat{j}\) + 1.0\(\hat{k}\)) m/s，对它的力为\(\vec{F}\) = (10.0\(\hat{i}\) + 15.0\(\hat{j}\)) N (a) 什么是粒子关于原点的角动量？ (b) 粒子围绕原点的扭矩是多少？ (c) 此时粒子角动量的时间变化率是多少？
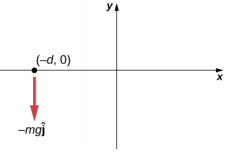
    5. 质量为 m 的粒子掉落在点 (−d, 0) 处，然后垂直落在地球的引力场 −g 中\(\hat{j}\)。 (a) 粒子围绕 z 轴的角动量的表达式是什么，它直接指向页外，如下所示？ (b) 计算粒子围绕 z 轴的扭矩。 (c) 扭矩是否等于角动量的时间变化率？

    显示了一个 x y 坐标系，正的 x 向右，正 y 向上。 粒子显示在 x 轴上，在 y 轴的左侧，位置减去 d 逗号零。 减去 m g j 的力向下作用于粒子。

    1. (a) 计算地球绕太阳轨道的角动量。 (b) 将该角动量与地球绕其轴线的角动量进行比较。
    2. 一块质量为 20 kg、半径为 20 cm 的巨石从静止处 15 米高的山坡上滚下来。 当它下山一半时，它的角动量是多少？ (b) 在底部？
    3. 一颗卫星以 6.0 rev/s 的速度旋转。该卫星由一个半径为 2.0 m、质量为 10,000 kg 的球体形状的主体和从主体质心伸出的两根天线组成，每个天线可以用长度为 3.0 m、质量为 10 kg 的杆近似接触。 天线位于旋转平面上。 卫星的角动量是多少？
    4. 螺旋桨由两个叶片组成，每个叶片长 3.0 米，每个叶片重达 120 千克。 螺旋桨可以通过绕其质心旋转的单根杆来近似。 螺旋桨从静止状态开始，在 30 秒内以恒定速度旋转至 1200 rpm。 (a) t = 10 s；t = 20 s 时螺旋桨的角动量是多少？ (b) 螺旋桨的扭矩是多少？
    5. 脉冲星是一种快速旋转的中子星。 金牛座星座中的螃蟹星云脉冲星的周期为33.5 x 10 −3 秒，半径为10.0 km，质量为2.8 x 10 30 kg。 由于释放电磁辐射，脉冲星的旋转周期将随着时间的推移而增加，电磁辐射不会改变其半径，但会降低其旋转能量。 (a) 脉冲星的角动量是多少？ (b) 假设角速度以 10 −14 rad/s 2 的速度降低。 脉冲星的扭矩是多少？
    6. 风力涡轮机的叶片长 30 m，最大旋转速度为 20 转/分钟。 (a) 如果每个叶片重量为6000千克，并且转子组件有三个叶片，则计算涡轮机在该旋转速率下的角动量。 (b) 在 5 分钟内将刀片旋转到最大旋转速度所需的扭矩是多少？
    7. 过山车的重量为3000.0 kg，需要安全地穿过半径为50.0 m的垂直圆环。环路底部的过山车的最小角动量是多少，才能安全通过？ 忽略赛道上的摩擦。 把过山车当成点粒子。
    8. 一名山地车手在比赛中跳跃然后空降。 山地自行车在空降之前以 10.0 m/s 的速度行驶。 如果自行车前轮的质量为 750 g，半径为 35 cm，那么自行车离开地面的那一刻旋转车在空中的角动量是多少？

    11.3 角动量守恒

    1. 质量为 2.0 kg、半径 60 cm 的圆盘，边缘附有 0.05 kg 的小质量块，正以 2.0 转/秒的速度旋转。小块物突然与圆盘分离。 磁盘的最终旋转速率是多少？
    2. 太阳的质量为 2.0 x 10 30 kg，其半径为 7.0 x 10 5 km，旋转周期约为 28 天。 如果太阳崩溃成半径为3.5 x 10 3 km的白矮星，那么如果没有质量被喷射并且密度均匀的球体可以在太阳之前和之后建模，那么它的周期会是多少？
    3. 具有旋转惯性的气缸 I 1 = 2.0 kg • m 2 绕垂直轴顺时针旋转穿过其中心，角速度\(\omega_{1}\) = 5.0 rad/s。第二个具有旋转惯性的气缸 I 2 = 1.0 kg • m 2 绕同一轴逆时针旋转角速度\(\omega_{2}\) = 8.0 rad/s。如果气缸耦合在一起，它们具有相同的旋转轴，则组合的角速度是多少？ 摩擦损失了多少百分比的原始动能？
    4. 跳出高板的潜水员在身体完全伸展的情况下进行初始旋转，然后进入塔克并在击中水面之前向后翻筋斗。 如果他在翻筋斗之前的惯性矩为 16.9 kg • m 2，翻筋斗期间的翻筋斗之后的惯性矩为 4. 2 kg • m 2，那么如果他在撞水之前花了 1.4 秒才执行翻筋斗，他必须直接从棋盘上给身体施加多少旋转速度？
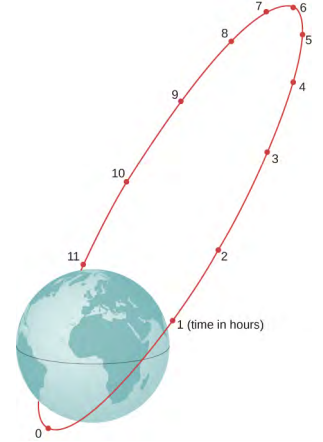
    5. 地球卫星的远地点在距离地球表面2500千米处，近地点位于离地球表面500千米处。 在远地点，它的速度为 730 m/s。它在近地点的速度是多少？ 地球的半径为 6370 km（见下文）。

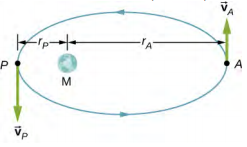
    椭圆逆时针轨道的示意图。 长轴是水平的，质量 M 位于左侧焦点，中心左侧。 位置 A 位于椭圆的最右边，距质量 M 右侧 r sub A 的距离 r sub A。点 A 处的速度是向量 v sub A 并且向上。 位置 P 位于椭圆的最左边缘，距离左质量 M 为 r sub p。点 P 处的速度是向量 v sub P 并且向下。

    1. 闪电轨道是通信卫星的高偏心轨道，旨在为斯堪的纳维亚国家和邻近的俄罗斯提供持续的通信覆盖。 轨道的定位使这些国家能够在很长一段时间内看到卫星（见下文）。 如果在这样一个轨道上的卫星从地球中心测得的远地点为40,000.0 km，速度为3.0 km/s，那么它在200.0 km高度测得的近地点的速度是多少？

    图中显示了绕地球的高偏心椭圆轨道。 地球位于椭圆的一个焦点上。轨道上标记了与时间（以小时为单位）对应的11个点。 时间 0 位于近地点（轨道上离地球最近的点），点 6 位于远地点，即轨道上离地球最远的点。 轨道上点 0 到 6 的间距随着时间的推移而减小，从 6 到 11 再返回 0 的间距增加。

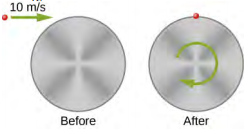
    1. 下图是一个质量为 20 g 的小颗粒，当它碰撞并粘在均匀的实心圆柱的边缘时，它以 10.0 m/s 的速度移动。 圆柱体可以绕其轴线自由旋转，穿过其中心，并且垂直于页面。 圆柱体的质量为 0.5 kg，半径为 10 cm，最初处于静止状态。 (a) 碰撞后系统的角速度是多少？ (b) 碰撞中损失了多少动能？

    粒子与圆柱体碰撞的视图显示在碰撞之前和之后。 圆柱体的表面位于页面的平面上。 以前，粒子以每秒 10 米的速度水平向圆柱体的顶部边缘移动。 气缸处于静止状态。 之后，粒子粘在圆柱体上，圆柱体正在顺时针旋转。

    1. 质量为0.020 kg的虫子静止在实心圆柱形圆盘（M = 0.10 kg，R = 0.10 m）的边缘，围绕垂直轴穿过其中心在水平面上旋转。 磁盘以 10.0 rad/s 的速度旋转。错误会爬到磁盘的中心。 (a) 圆盘的新角速度是多少？ (b) 系统的动能发生了什么变化？ (c) 如果错误爬回磁盘的外边缘，那么磁盘的角速度是多少？ (d) 系统的新动能是多少？ (e) 动能增加和减少的原因是什么？
    2. 质量为 200 g、长 100 cm 的均匀杆可以在水平面上围绕固定的垂直轴自由旋转，穿过其中心，垂直于其长度。 两个小珠子，每个重量为 20 g，安装在杆上的凹槽中。 最初，这两颗珠子由鱼竿中心两侧的扣环固定，距离旋转轴线 10 厘米。 当珠子处于这个位置时，鱼竿以 10.0 rad/s 的角速度旋转。当捕获物被释放时，珠子会沿着杆向外滑动。 (a) 当珠子到达棒的末端时，棒的角速度是多少？ (b) 如果珠子从杆上飞下来，棒的角速度是多少？
    3. 旋转木马的半径为 2.0 m，惯性矩为 300 kg • m 2。 一个体重为 50 kg 的男孩以 4.0 m/s 的速度与轮缘切线奔跑然后跳起来。 如果旋转木马最初处于静止状态，那么男孩跳上去后的角速度是多少？
    4. 游乐场旋转木马的质量为 120 kg，半径为 1.80 m，它以 0.500 rev/s 的角速度旋转。一个 22.0 千克的孩子抓住它的外缘进入游乐场后，它的角速度是多少？ 孩子最初处于休息状态。
    5. 三个孩子骑在旋转木马的边缘，旋转木马重量为 100 kg，半径为 1.60 米，以 20.0 rpm 的速度旋转。 孩子们的体重分别为22.0、28.0和33.0千克。 如果重量为28.0 kg的孩子移动到旋转木马的中心，那么新的角速度（以rpm为单位）是多少？
    6. (a) 计算滑冰运动员以 6.00 转/秒旋转的角动量，假设他的惯性矩为 0.400 kg • m 2。 (b) 他通过伸出手臂和增加惯性矩来降低旋转速度（角速度）。 如果他的角速度减小到 1.25 rev/s，则找出他的惯性矩的值。(c) 假设他保持双臂在里面，让冰的摩擦使他减速到 3.00 rev/s。如果这需要 15.0 秒，平均施加的扭矩是多少？
    7. 如下图所示，双子滑冰运动员互相接近并锁住双手。 (a) 计算它们的最终角速度，假设每个角速度相对于冰的初始速度为2.50 m/s。 每个人的质量为 70.0 kg，每个质量中心距离锁住的双手 0.800 m。 你可以将它们的惯性矩近似为该半径处点质量的惯性矩。 (b) 比较初始动能和最终动能。

    左边的图 a 是两名滑冰运动员的图，从上方看，他们沿着平行线以速度 v 向对方移动。 上面的向右滑冰，下面的向左滑冰，它们是分开的，这样他们就可以在交叉时双手相遇。 右边的图 b 显示了滑冰运动员手牵手一起以角速度欧米茄围成一圈移动。 从上方看，它们的运动是顺时针的。

    1. 棒球接球手直向上伸出手臂，以 40 m/s 的速度接球。棒球为 0.145 kg，接球手的手臂长度为 0.5 m，质量为 4.0 kg。 (a) 从手臂窝测量，接球后手臂立即的角速度是多少？ (b) 如果接球手在接球 0.3 秒后停止手臂旋转，施加的扭矩是多少？
    2. 2015年，在波兰华沙，新斯科舍省的奥利维亚·奥利弗打破了世界纪录，成为滑冰鞋速度最快的运动员。 她创下了创纪录的342转/分钟，超过了现有的吉尼斯世界纪录34次。 如果滑冰运动员以这种旋转速度伸出双臂，那么她的新旋转速度会是多少？ 假设在创纪录的旋转中，她可以用一根高 1.7 米、半径为 15 厘米的 45 千克杆近似值。 伸展双臂时，取近似一根长度为130厘米的杆，其体重的10％垂直于旋转轴对齐。 忽略摩擦力。
    3. 地球同步环形轨道上的卫星距离地球中心42,164.0公里。 一颗小行星与卫星碰撞，将其送入远地点45,000.0 km的椭圆轨道。 卫星在远地点的速度是多少？ 假设它的角动量是守恒的。
    4. 体操运动员沿着地板做手推车，然后将自己发射到空中，并在空降时用塔克进行几次翻转。 如果她在执行手推车时的惯性矩为 13.5 kg • m 2 而她的旋转速率为 0.5 rev/s，那么如果她在塔克中的惯性矩为 3.4 kg • m 2 并且她有 2.0 秒的时间在空中翻转，她在空中会转多少圈？
    5. 美国宇航局艾姆斯研究中心的离心机半径为8.8米，可在其有效载荷上产生20 gs的力，或地球上重力的20倍。 (a) 在离心机中承受 10 gs 的 20 千克有效载荷的角动量是多少？ (b) 如果驱动器马达在 (a) 中关闭，有效载荷损失了 10 千克，那么考虑到没有摩擦力，它的新旋转速度会是多少？
    6. 在狂欢节上骑行有四个辐条，上面装有吊舱，可以容纳两个人。 每个辐条长 15 m，附着在中心轴上。 每个辐条的质量为 200.0 千克，每个轮辐的质量为 100.0 千克。 如果骑行以 0.2 rev/s 的速度旋转，每个吊舱包含两个 50.0 公斤的孩子，那么如果所有孩子都跳下骑行，新的旋转速度是多少？
    7. 一名滑冰运动员正在准备轮流跳跃，双臂伸出。 当他的双臂伸展时，他的惯性矩为 1.8 kg • m 2，他以 0.5 rp/s 的速度旋转。如果他以 9.0 m/s 的速度与冰以 45° 的角度向空中发射自己，那么如果他在空中的惯性矩为 0.5 kg • m 2？
    8. 空间站由一个质量为10 6 千克的巨大旋转空心圆柱体组成，包括空间站上的人，半径为100.00 m。它以3.30转/分钟在太空中旋转，以产生人造重力。 如果100个人平均质量为65.00千克的太空行走到等待中的太空飞船上，那么当所有人都离开空间站时，新的旋转速度是多少？
    9. 海王星的质量为1.0 x 10 26 千克，距离太阳 4.5 x 10 9 千米，轨道周期为 165 年。 45 亿年前，外部原始太阳系中的 Planetesimals 在数亿年的时间里聚集成了海王星。 如果演变为当今太阳系的原始圆盘的半径为10 11 km，如果构成这些后来成为海王星的小行星的物质均匀地分布在它的边缘，那么原始圆盘外缘的轨道周期是多少？

    11.4 陀螺仪的进动

    1. 陀螺仪有一个 0.5 千克的圆盘，以 40 转/秒的速度旋转。圆盘的质心距离枢轴 10 厘米，轴心也是圆盘的半径。 进动角速度是多少？
    2. 陀螺仪的进动角速度为 1.0 rad/s。如果旋转圆盘的质量为 0.4 kg，其半径为 30 cm，以及从质心到枢轴的距离，则圆盘的旋转速率是多少？
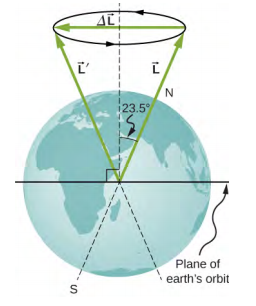
    3. 地球轴线呈23.5°角，其方向垂直于地球轨道平面。 如下所示，该轴向前移动，在 25,780 y 内完成一次旋转。(a) 计算这次角动量变化一半。 (b) 产生这种角动量变化的平均扭矩是多少？ (c) 如果这个扭矩是由一对作用在赤道上最有效点的力产生的，那么每种力的大小会是多少？

    图中显示了地球的图像。 地球轨道的平面在赤道处显示为一条水平线。 地球的南北轴与垂直方向成23.5度的角度倾斜。 有两个向量，L 和 L 素数，从地球中心开始，以与垂直方向成二十三点五度的角度倾斜。 向量 L 穿过地球的北极。 在两个向量的头部有一个圆，从上方看，它以逆时针方向指向。 显示了沿其直径向左指向的角动量矢量 Delta L。

    其他问题

    1. 当大理石启动向水平倾斜30°的平面时，它正以7.0 m/s的速度在地板上滚动。 (a) 在休息之前，大理石会沿飞机行驶多远？ (b) 大理石在飞机上移动需要多长时间？
    2. 重复前面的问题，用空心球替换大理石。 解释新的结果。
    3. 半径为 1.0 m 的圈环的质量为 6.0 千克。 它以 10.0 m/s 的速度在水平表面上滚动。(a) 停止圈环需要多少工作？ (b) 如果环状物以 10.0 m/s 的速度在水平线 30° 处开始表面，那么在停下来向下滚动之前，它会沿着斜坡行驶多远？
    4. 对半径、质量和初始速度相同的空心球体重复上述问题。 解释结果的差异。
    5. 粒子的质量为 0.5 kg，正向 y 方向以 2.0 m/s 的速度沿线 x = 5.0 m 移动。 粒子关于原点的角动量是多少？
    6. 一个 4.0 kg 的粒子在半径为 2.0 m 的圆中移动。粒子的角动量根据 l = 5.0t 2 的时间而变化。 (a) t = 3.4 秒时，粒子绕圆心的扭矩是多少？ (b) t = 3.4 秒时粒子的角速度是多少？
    7. 质子在回旋加速器中在 0.01 秒内加速到 5.0 x 10 6 m/s。质子沿着圆形路径行驶。 如果回旋加速器的半径为 0.5 km，(a) 质子在最大速度下围绕中心的角动量是多少？ (b) 质子加速到最大速度时中心周围的扭矩是多少？
    8. (a) 月球在环绕地球的轨道上的角动量是多少？ (b) 这种角动量与月球在其轴上的角动量相比如何？ 请记住，月球始终保持一侧朝向地球。
    9. 一张 DVD 以 500 转速旋转。 如果半径为 6.0 cm，质量为 20.0 g，DVD 的角动量是多少？
    10. 陶艺圆盘在 15 秒内从静止状态旋转到 10 转/秒。圆盘的质量为 3.0 kg，半径为 30.0 cm。 t = 5 s、t = 10 s 时圆盘的角动量是多少？
    11. 假设你通过在曲柄上施加 300 N 的力持续 0.250 秒来启动一辆古董车。如果曲柄距离枢轴 0.300 m，并且始终施加力以产生最大扭矩，则发动机的角动量是多少？
    12. 质量为 2.0 kg、半径为 20 cm 的实心圆柱体以 600 转/分钟的速度绕垂直轴逆时针旋转穿过其中心。 第二个相同质量的实心圆柱体以 900 rev/min 的速度绕同一垂直轴顺时针旋转。 如果圆柱耦合使它们围绕相同的垂直轴旋转，那么组合的角速度是多少？
    13. 一个男孩站在平台的中央，该平台以 1.0 转/秒的速度无摩擦地旋转。男孩将重量尽可能远离身体。 在这个位置上，男孩、平台和重量的总惯性矩为 5.0 kg • m 2。 男孩将重量拉到身体附近，从而将总惯性矩降低到 1.5 kg • m 2。 (a) 平台的最终角速度是多少？ (b) 旋转动能增加了多少？
    14. 八个孩子爬上小型旋转木马，每个体重为40公斤。 他们将自己均匀地放在外缘并携起手来。 旋转木马的半径为 4.0 m，惯性矩为 1000.0 kg • m 2。 当旋转木马的角速度为 6.0 rev/min 后，孩子们向内行走，当他们距离旋转轴 0.75 米时停下来。 旋转木马的新角速度是多少？ 假设结构上的摩擦扭矩可以忽略不计。
    15. 质量为 150 g 的薄米棒以 240 转/分钟的角速度围绕垂直于棒长轴的轴旋转。 如果旋转轴 (a) 穿过摇杆的中心，摇杆的角动量是多少？ (b) 穿过棍子的一端？
    16. 一颗质量为20,000 kg、半径为5.0 m的球体形状的卫星正绕着一条轴线旋转，穿过其质心。 它的旋转速率为 8.0 rev/s。两根天线部署在从卫星质心延伸的旋转平面上。 每根天线都可以近似化，因为一根杆的质量为 200.0 kg，长度为 7.0 m。卫星的新旋转速率是多少？
    17. 顶部的惯性矩 3.2 x 10 −4 kg • m 2，从质心到枢轴点的半径为 4.0 cm。 如果它以 20.0 转速/秒旋转并且正在前进，那么它在 10.0 秒内会进行多少转？

    挑战问题

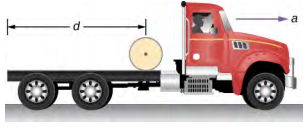
    1. 下图所示的卡车最初处于静止状态，床上有一卷坚固的圆柱形纸。 如果卡车以均匀的加速度 a 向前移动，那么在纸张从后端滚出之前，它会移动多远的距离？ （提示：如果滚动以 a′ 向前加速，则相对于卡车向后加速，加速度为 a − a′。 另外，R\(\alpha\) = a − a′。）

    一张平板卡车在水平道路上的图。 卡车正通过加速 a 向前加速。卡车底座上有一个气缸，距离底盘后端有一段距离 d。

    1. 半径为 8.5 cm 的保龄球以 9.0 m/s 的速度被扔到保龄球道上。如观察者所见，投掷方向向左，因此保龄球在与地板接触时开始逆时针旋转。 车道上的动摩擦系数为 0.3。 (a) 球需要多长时间才能达到不会滑倒的地步？ 到球在没有滑动的情况下滚动点的距离 d 是多少？
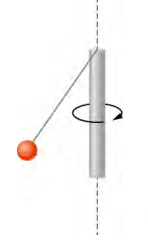
    2. 质量为 0.50 kg 的小球通过一根无质量的绳子连接到正在旋转的垂直杆上，如下所示。 当杆的角速度为 6.0 rad/s 时，绳子相对于垂直方向的角度为 30°。 (a) 如果角速度增加到 10.0 rad/s，则弦的新角度是多少？ (b) 计算球的初始和最终角力矩。 (c) 球杆旋转得足够快以使球处于水平状态吗？

    垂直杆在其轴线上旋转。 一端有一根绳子固定在杆的顶部，另一端有一根球。 绳子与杆成一定角度垂下。

    1. 以 1.0 m/s 的速度水平飞行的虫子碰撞并粘在垂直悬挂的均匀棍子的末端。 撞击后，摇杆向外摆动至垂直方向的最大角度为 5.0°，然后向后旋转。 如果棍子的质量是虫子的10倍，则计算棍子的长度。

    贡献者和归因

    Template:ContribOpenStaxUni