11.5: 陀螺仪的进动

Last updated
Save as PDF

Page ID: 204356

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

描述进动现象背后的物理过程
计算陀螺仪的进动角速度

图中\(\PageIndex{1}\)显示了一个陀螺仪，它被定义为旋转盘，其中的旋转轴可以自由地呈现任何方向。旋转时，自旋轴的方向不受围绕自旋轴的主体方向的影响。封闭陀螺仪的车身或车辆可以从一个地方移动到另一个地方，旋转轴的方向将保持不变。这使得陀螺仪在导航中非常有用，尤其是在无法使用磁罗盘的地方，例如载人和无人驾驶航天器、洲际弹道导弹、无人驾驶飞行器和哈勃太空望远镜等卫星。

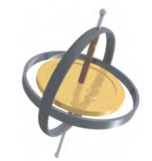
陀螺仪的绘图，由一个圆盘组成，该圆盘可以在轴上旋转，垂直于圆盘的平面并穿过其中心。陀螺仪周围有两个环。一个固定在圆盘上方和下方的轴上，另一个附着在第一个环上，位于圆盘的平面上，因此第二个环与圆盘同心。 — 图\(\PageIndex{1}\)：陀螺仪由一个绕轴旋转的圆盘组成，该轴可以自由地假设任何方向。

在接下来的两幅图中，我们用顶部的示例来说明陀螺仪的旋转。如果顶部放置在地球表面附近的平坦表面上，与垂直方向成一定角度，并且没有旋转，它就会掉落，因为重力会产生作用于其质心的扭矩。如图所示\(\PageIndex{2a}\)。但是，如果顶部在其轴线上旋转，而不是因为这种扭矩而倾倒，它会绕垂直方向移动，如所示\(\PageIndex{2b}\)。这是由于质心上的扭矩造成了角动量的变化。

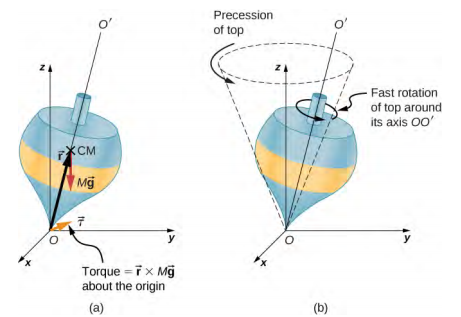
图 a：显示了 x y z 坐标系，其中 x 在页面外，y 向右，z 向上。原点是 O 点。顶部显示的是其点位于原点，其轴偏离垂直 z 轴。顶部的轴是直线 O O 素数。向量 r 从顶部的原点延伸到质心，标记为 C M。力 M g 在质心向下起作用。围绕原点的扭矩等于矢量 r 与 M 向量 g 交叉。该扭矩是 x y 平面中的一个矢量，垂直于 r 向量。图 b：显示了 x y z 坐标和顶部。从上方看，顶部再次偏离 z 轴，并围绕 O O prime 轴快速逆时针旋转。从上方看，顶部的进动沿逆时针方向走一个以 z 轴为中心的圆圈。顶部进动所横扫的圆锥用虚线表示。 — 图\(\PageIndex{2}\)：(a) 如果顶部没有旋转，则原点周围\(\vec{r} \times M\vec{g}\)有扭矩，顶部会掉下来。 (b) 如果顶部围绕其轴线旋转 OO′，则它不会掉下来，而是围绕 z 轴移动。

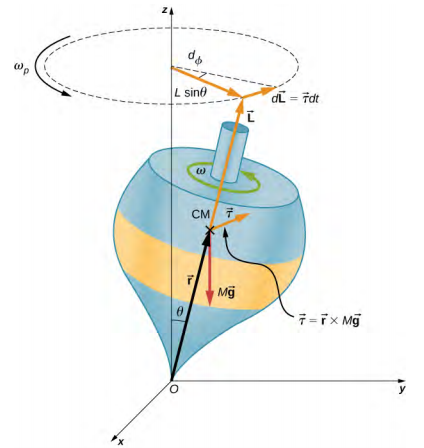
该图\(\PageIndex{3}\)显示了作用在旋转陀螺上的力。产生的扭矩垂直于角动量矢量。这会\(\vec{L}\)根据 d\(\vec{L}\) =\(\vec{\tau}\) dt 改变角动量向量的方向，但不会改变其大小。顶部绕垂直轴移动，因为扭矩始终水平且垂直于\(\vec{L}\)。如果顶部没有旋转，它会在扭矩方向上获得角动量，然后绕水平轴旋转，像我们预期的那样掉落。

显示 x y z 坐标系，x 在页面外，y 向右，z 向上。原点是点 O。当我们观察时，顶部的点位于原点，其轴向垂直 z 轴倾斜一个角度 theta，顺时针方向。向量 r 从顶部的原点延伸到质心，标记为 C M。力 M g 在质心向下起作用。围绕原点的扭矩 tau 等于矢量 r 与 M 向量 g 交叉。该扭矩是 x y 平面中垂直于 r 向量进入页面的向量。从上方看，顶部的角速度欧米茄是逆时针方向的。角动量 L 与 r 向量的方向相同，沿着顶部的轴向上倾斜。由顶部进动所描绘的圆显示为顶部上方的水平圆圈。从上方看，进动角速度 omega sub p 是逆时针方向的。进动圆的半径为 L 正弦西塔。向量 d L 与圆相切，指向页面，等于向量 tau d t。显示了形成 L sine theta 和 d L 的三角形，与 d L 的对角被标记为 d phi。 — 图\(\PageIndex{3}\)：作用于质心的重力会在垂直\(\vec{\tau}\)的方向上产生扭矩\(\vec{L}\)。的大小\(\vec{L}\)没有变化，但其方向会改变，顶部围绕 z 轴移动。

我们可以通过握住旋转的自行车车轮并尝试绕垂直于旋转轴的轴旋转它来亲身体验这种现象。如图所示\(\PageIndex{4}\)，该人施加垂直于旋转轴的力试图旋转车轮，但相反，由于施加的扭矩，轮轴开始向左改变方向。

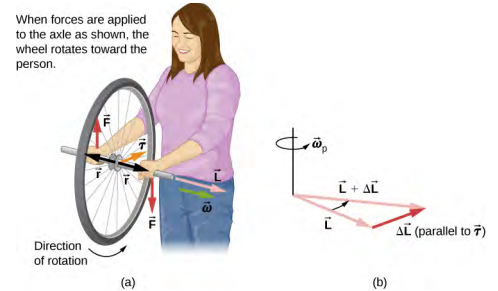
在图 a 中，一位女士正面对观众，在车轴旁拿着半径为 r 的旋转自行车车轮。轮子是这样的，角速度 omega 和角动量 L 沿着轮子的旋转轴向左（观众的右边）。也就是说，轮子的运动使得轮子的底部向她移动（进入页面）。她左手施加的力 F 的方向向下显示，右手向上显示的方向。扭矩 tau 朝向她（进入页面）在图 b 中，显示了两个矢量 L 和 delta-L 的加法，它们平行于扭矩 tau。两个向量的结果被标记为 L 加增量 L。从上方看，旋转方向 omega sub p 是逆时针方向。 — 图\(\PageIndex{4}\)：(a) 一个拿着旋转自行车车轮的人用右手抬起车轮，然后用左手向下推，试图旋转方向盘。这个动作会直接向她产生扭矩。这种扭矩会导致角动量\(\Delta \vec{L}\)在完全相同的方向上发生变化。 (b) 描绘如何\(\vec{L}\)添加\(\Delta \vec{L}\)和添加的矢量图，产生新的角动量，更多地指向人。轮子向人移动，垂直于她对人施加的力。

我们都知道自行车在休息时坐在自行车上翻倒是多么容易。但是，当自行车以良好的速度骑行时，很难将其翻倒，因为我们必须改变旋转车的角动量矢量。

注意

观看这段关于陀螺仪进动的视频，完整演示自行车车轮的进动。

另外，当将旋转的磁盘放入诸如蓝光播放器之类的盒子中时，请尝试将其移动。向给定方向平移盒子很容易，但很难绕垂直于旋转盘轴线的轴线旋转，因为我们在盒子上施加扭矩，这将导致旋转盘的角动量向量移动。

我们可以在图中计算出顶部的进动率\(\PageIndex{3}\)。从图\(\PageIndex{3}\)中可以看出，扭矩的大小是

\[\tau = rMg \sin \theta \ldotp\]

因此，

\[dL = rMg \sin \theta dt \ldotp\]

顶部在时间 dt 中穿过的角度为

\[d \phi = \frac{dL}{L \sin \theta} = \frac{rMg \sin \theta}{L \sin \theta} dt = \frac{rMg}{L} dt \ldotp\]

进动角速度是\(\omega_{P} = \frac{d \phi}{dt}\)，从这个方程中我们可以看出

\[\omega_{P} = \frac{rMg}{L} \ldotp\]

或者，由于 L = I\(\omega\)，

\[\omega_{P} = \frac{rMg}{I \omega} \ldotp \label{11.12}\]

在此推导中，我们假设\(\omega_{P}\) <<\(\omega\)，也就是说，进动角速度远小于陀螺盘的角速度。进动角速度为沿 z 轴的角动量增加了一个很小的分量。这可以从陀螺仪移动时向上和向下轻微的摆动中看出，被称为 nutation。

地球本身就像一个巨大的陀螺仪。它的角动量沿其轴线，目前指向北极星北极星。但是，由于太阳和月亮在其非球形形状上的扭矩，地球正在缓慢前进（大约每26,000年一次）。

示例\(\PageIndex{1}\): Period of Precession

陀螺仪的尖端在地面上旋转，旋转时的摩擦阻力可以忽略不计。陀螺仪的圆盘质量为 0.3 kg，以 20 转/秒的速度旋转。其质心距离枢轴 5.0 cm，圆盘半径为 5.0 cm。陀螺仪的进动周期是多少？

策略

我们使用方程\ ref {11.12} 来计算陀螺仪的进动角速度。这使我们能够找到进动时期。

解决方案

磁盘的惯性矩为

\[I = \frac{1}{2} mr^{2} = \frac{1}{2} (0.30\; kg)(0.05\; m)^{2} = 3.75 \times 10^{-4}\; kg\; \cdotp m^{2} \ldotp \nonumber\]

圆盘的角速度为

\[20.0\; rev/s = (20.0)(2 \pi)\; rad/s = 125.66\; rad/s \ldotp \nonumber\]

我们现在可以在方程式\ ref {11.12} 中进行替换。进动角速度为

\[\omega_{P} = \frac{rMg}{I \omega} = \frac{(0.05\; m)(0.3\; kg)(9.8\; m/s^{2})}{(3.75 \times 10^{-4}\; kg\; \cdotp m^{2})(125.66\; rad/s)} = 3.12\; rad/s \ldotp \nonumber\]

陀螺仪的进动周期是

\[T_{P} = \frac{2 \pi}{3.12\; rad/s} = 2.0\; s \ldotp \nonumber\]

意义

陀螺仪的进动角频率为3.12 rad/s，或大约 0.5 rev/s，远低于陀螺仪盘的角速度 20 rev/s。因此，我们预计角动量的很大一部分不会由于进动而产生，而方程11.12是进动角速度的良好近似值。

练习\(\PageIndex{1}\)

顶部在地球上的进动频率为 5.0 rad/s。它在月球上的进动频率是多少？