11.4: 角动量守恒
- Page ID
- 204395
- 应用角动量守恒来确定惯性矩正在变化的旋转系统的角速度
- 解释当系统的惯性矩和角速度发生变化时,旋转动能是如何变化的
到目前为止,我们已经研究了由点粒子和刚体组成的系统的角动量。 我们还使用将外部净扭矩与角动量变化联系起来的表达式分析了所涉及的扭矩。 遵循该方程式的系统示例包括自由旋转的自行车轮胎,该轮胎由于摩擦产生的扭矩而随着时间的推移而减速,或者由于对潮汐变形施加的摩擦力而导致地球的自转速度在数百万年内减慢。
但是,假设系统上没有净外部扭矩,\(\sum \vec{\tau}\)= 0。 在这种情况下,我们可以介绍角动量守恒定律。
如果固定惯性参考系中某一点周围没有净外部扭矩,则粒子系统围绕该点的角动量将保持不变:
\[\frac{d \vec{L}}{dt} = 0 \label{11.10}\]
要么
\[\vec{L} = \vec{l}_{1} + \vec{l}_{2} + \cdots + \vec{l}_{N} = constant \ldotp \label{11.11}\]
请注意,总角动量\(\vec{L}\)是守恒的。 只要它们的总和保持不变,任何单个角力矩都可以改变。 该定律类似于当系统上的外力为零时保持线性动量。
作为角动量守恒的示例,图中\(\PageIndex{1}\)显示了一名滑冰运动员正在进行旋转。 她的净扭矩非常接近于零,因为她的溜冰鞋和冰之间的摩擦力相对较小。 此外,摩擦力施加在非常靠近轴心点的地方。 \(|\vec{F}|\)和都\(|\vec{r}|\)很小,所以可以忽略\(|\vec{\tau}|\)不计。 因此,她可以旋转相当长的一段时间。 她还可以通过拉动手臂和腿来提高旋转速度。 为什么拉她的胳膊和腿会提高她的旋转速度? 答案是她的角动量是恒定的,所以
\[L' = L\]
要么
\[I' \omega' = I \omega,\]
其中,底漆量是指她拉起手臂并减少惯性矩之后的状况。 由于 I′ 较小,因此必须增加角速度\(\omega\) ′ 才能保持角动量恒定。
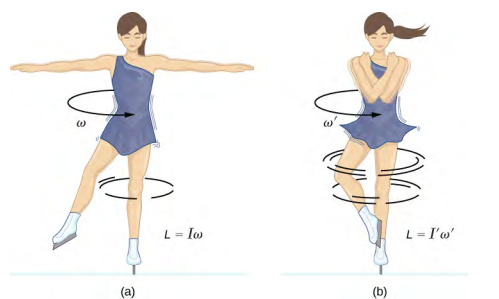
有趣的是,当滑冰运动员拉进手臂时,她的旋转动能是如何变化的。 她最初的旋转能量是
\[K_{Rot} = \frac{1}{2} I \omega^{2},\]
而她最后的旋转能量是
\[K'_{Rot} = \frac{1}{2} I (\omega')^{2} \ldotp\]
由于 I'\(\omega\) ′ = I\(\omega\),我们可以用 '代替\(\omega\)' 然后找到
\[K'_{Rot} = \frac{1}{2} I' (\omega')^{2} = \frac{1}{2} I' \left(\dfrac{I}{I'} \omega \right)^{2} = \frac{1}{2} I \omega^{2} \left(\dfrac{I}{I'}\right) = K_{Rot} \left(\dfrac{I}{I'}\right) \ldotp\]
因为她的惯性矩减少了\(I′ < I\),所以她的最终旋转动能增加了。 这种额外的旋转动能的来源是将她的手臂向内拉动所需的工作。 请注意,滑冰运动员的手臂不会以完美的圈子移动,它们会向内旋转。 这项工作导致旋转动能增加,而她的角动量保持不变。 由于她处在无摩擦的环境中,任何能量都无法逃脱系统。 因此,如果她将手臂伸展到原来的位置,她将以原始角速度旋转,动能将恢复到其原始值。
太阳系是角动量守恒在我们的宇宙中如何运作的又一个例子。 我们的太阳系是从一团巨大的气体和尘埃中诞生的,这些气体和尘埃最初具有旋转能量。 引力导致云层收缩,角动量守恒导致旋转速率增加(图\(\PageIndex{2}\))。
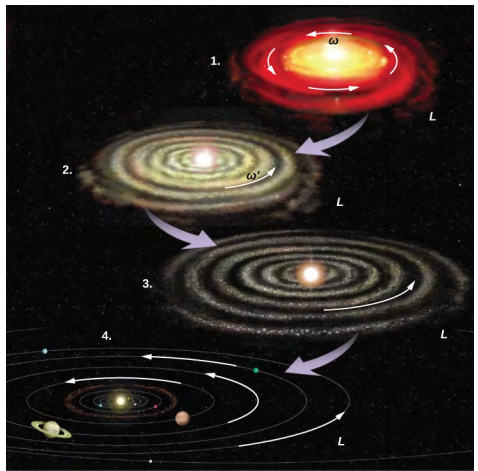
我们继续讨论一个具有工程应用的示例。
飞轮在旋转惯性可以忽略不计的无摩擦垂直轴上以\(\omega_{0}\) = 600 转/分钟的角速度 = 600 rev/min 旋转。 第二个飞轮掉落在上面,它处于静止状态,其惯性矩是旋转飞轮的三倍(图\(\PageIndex{3}\))。 由于表面之间存在摩擦力,飞轮很快就会达到相同的旋转速度,之后它们会一起旋转。
- 使用角动量守恒定律来确定组合\(\omega\)的角速度。
- 飞轮耦合过程中损失了多少初始动能?
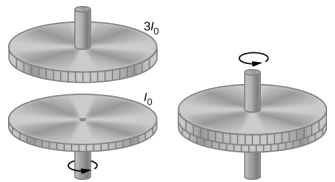
策略
第 (a) 部分很容易求解耦合系统的角速度。 我们使用 (a) 的结果来比较 (b) 部分中系统的初始和最终动能。
解决方案
- 外部扭矩不会作用于系统。 摩擦产生的力会产生内部扭矩,这不会影响系统的角动量。 因此,角动量的守恒可以得到\[I_{0} \omega_{0} = (I_{0} + 3I_{0}) \omega, \nonumber\]\[\omega = \frac{1}{4} \omega_{0} = 150\; rev/min = 15.7\; rad/s \ldotp \nonumber\]
- 在接触之前,只有一个飞轮在旋转。 该飞轮的旋转动能是系统的初始旋转动能\(\frac{1}{2} I_{0} \omega_{0}^{2}\)。 \[\frac{1}{2} (4I_{0}) \omega^{2} = \frac{1}{2} (4I_{0}) \left(\dfrac{\omega_{0}}{4}\right)^{2} = \frac{1}{8} I_{0} \omega_{0}^{2}. \nonumber\]因此,最终动能与初始动能之比为\[\frac{\frac{1}{8} I_{0} \omega_{0}^{2}}{\frac{1}{2} I_{0} \omega_{0}^{2}} = \frac{1}{4} \ldotp \nonumber\]因此,初始动能的3/4因两个飞轮的耦合而损失。
意义
正如角动量守恒定律所预期的那样,由于系统的旋转惯性增加,角速度降低了。 在这个例子中,我们看到系统的最终动能减少了,因为能量因飞轮的耦合而流失。 将此与 Figure 中的滑冰运动员\(\PageIndex{1}\)正在努力将手臂伸向内并增加旋转动能的例子进行比较。
操场上的旋转木马以 4.0 转/分的速度旋转。 三个孩子跳起来,将旋转木马/儿童旋转系统的惯性矩提高25%。 新的旋转速度是多少?
一名 80.0 公斤的体操运动员从高杆下车。 他在完全延伸时开始下车,然后在着陆前塞住以完成多次旋转。 他完全伸展时的惯性矩可以近似为一根长度为 1.8 米的杆,而在塔克中则可以近似为长度为该长度的一半的杆。 如果他在完全伸展时的旋转速率为 1.0 rev/s,当质心处于 3.0 m 高度时他进入塔克水平向地板移动,那么如果他以 1.8 米的高度从塔克中出来,他能执行多少转? 参见图\(\PageIndex{4}\)。
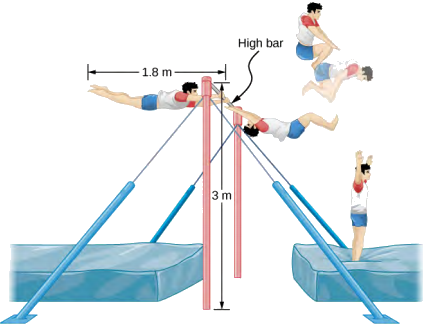
策略
利用角动量守恒,我们可以找到他在塔克中的旋转速率。 使用运动学方程,我们可以找到从 3.0 m 到 1.8 m 的高度之间的时间间隔。由于他相对于地面水平移动,自由落体方程简化了。 这将允许计算可以执行的转数。 由于我们使用的是比率,因此我们可以将单位保持为转速/秒,无需转换为弧度/秒。
解决方案
完全伸展时的惯性矩为\[I_{0} = \frac{1}{12} mL^{2} = \frac{1}{12} (80.0\; kg)(1.8\; m)^{2} = 21.6\; kg\; \cdotp m^{2} \ldotp \nonumber\]
塔克中的惯性矩是\[I_{f} = \frac{1}{12} mL_{f}^{2} = \frac{1}{12} (80.0\; kg)(0.9\; m)^{2} = 5.4\; kg\; \cdotp m^{2} \ldotp \nonumber\]
角动量守恒:\[I_{f} \omega_{f} = I_{0} \omega_{0} \Rightarrow \omega_{f} = \frac{I_{0} \omega_{0}}{I_{f}} = \frac{(21.6\; kg\; \cdotp m^{2})(1.0\; rev/s)}{5.4\; kg\; \cdotp m^{2}} = 4.0\; rev/s \ldotp \nonumber\]
时间间隔:\[t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2(3.0 - 1.8) m}{9.8\; m/s}} = 0.5\; s \ldotp \nonumber\]
在 0.5 秒内,他将能够以 4.0 转速/秒执行两次转速。
意义
请注意,他能完成的转数将取决于他在空中待了多长时间。 在问题中,他正在水平离开高杆到地面。 他也可以与地面成一定角度退出,根据相对于地面的正向或负角度,让他在空中停留的时间或多或少。 体操运动员在执行下车时必须考虑到这一点。
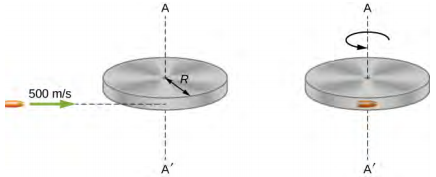
质量为 m = 2.0 g 的子弹以 500.0 m/s 的速度水平移动。子弹击中并嵌入质量为 M = 3.2 kg、半径 R = 0.5 m 的实心圆盘的边缘。圆柱体可以绕其轴线自由旋转,最初处于静止状态(图\(\PageIndex{5}\))。 子弹嵌入后磁盘的角速度是多少?
策略
对于子弹和圆柱体系统,没有外部扭矩沿着穿过圆盘中心的垂直轴起作用。 因此,沿该轴的角动量是守恒的。 子弹的初始角动量是 mVR,它是在碰撞前一刻绕圆盘的旋转轴拍摄的。 圆柱体的初始角动量为零。 因此,系统的净角动量为 mVR。 由于角动量是守恒的,因此系统的初始角动量等于撞击后立即嵌入圆盘中的子弹的角动量。
解决方案
系统的初始角动量为
\[L_{i} = mvR \ldotp \nonumber\]
将子弹嵌入磁盘的系统的惯性矩为
\[I = mR^{2} + \frac{1}{2} MR^{2} = \left(m + \dfrac{M}{2}\right) R^{2} \ldotp \nonumber\]
系统的最终角动量是
\[L_{f} = I \omega_{f} \ldotp \nonumber\]
因此,通过保持角动量,L i = L f 和
\[mvR = \left(m + \dfrac{M}{2}\right) R^{2} \omega_{f} \ldotp \nonumber\]
求解\(\omega_{f}\),
\[\omega_{f} = \frac{mvR}{\left(m + \dfrac{M}{2}\right) R^{2}} = \frac{(2.0 \times 10^{-3}\; kg)(500.0\; m/s)}{(2.0 \times 10^{-3}\; kg + 1.6\; kg)(0.50\; m)} = 1.2\; rad/s \ldotp \nonumber\]
意义
该系统由点粒子和刚体组成。 在计算碰撞前后的角动量时必须小心。 就在撞击之前,子弹的角动量是围绕圆盘的旋转轴拍摄的。


