11.3: 角动量

Last updated
Save as PDF

Page ID: 204373

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

描述角动量的向量性质
找出粒子系统指定原点周围的总角动量和扭矩
计算围绕固定轴旋转的刚体的角动量
计算绕固定轴旋转的刚体上的扭矩
在分析改变其旋转速率的物体时使用角动量守恒法

为什么地球会继续旋转？它一开始是怎么开始旋转的？为什么地球的引力吸引力没有使月球撞向地球？滑冰运动员如何仅凭双臂伸进来就能越来越快地旋转？为什么她不必施加扭矩就能更快地旋转？

这些问题的答案是，就像宇宙中的总线性运动（动量）是守恒的，总旋转运动也是守恒的。我们将总旋转运动称为角动量，即线性动量的旋转对应物。在本章中，我们首先定义角动量，然后从各种角度探索角动量。但是，首先，我们要研究单个粒子的角动量。这使我们能够为粒子系统和刚体开发角动量。

单粒子的角动量

图中$\PageIndex{1}$显示了一个粒子位于$\vec{r}$相对于原点的线性动量$\vec{p}$ = m$\vec{v}$ 的位置。即使粒子没有绕原点旋转，我们仍然可以根据位置向量和线性动量来定义角动量。

粒子的角动量

粒$\vec{l}$子的角动量被定义为$\vec{r}$和的交叉积$\vec{p}$，垂直于包含$\vec{r}$和的平面$\vec{p}$：

\[\vec{l} = \vec{r} \times \vec{p} \ldotp \label{11.5}\]

显示 x y z 坐标系，其中 x 指向页面，y 指向右侧，z 指向上方。向量 r 从原点指向第一象限 x y 平面中的某个点。从上方看，矢量从 r 向量的尖端指向，与 r 向量方向逆时针方向成一个 theta 的角度。 r 和 p 向量都在 x y 平面上。向量 l 指向上方，垂直于 x y 平面，符合右手定律。从上方看，当右手的手指逆时针卷曲时，拇指朝上 l 方向。我们还显示了与 p 向量平行和垂直的向量 r 的分量。向量 r sub perpendicular 是垂直于 p 向量方向的 r 向量的投影。 — 图$\PageIndex{1}$：在三维空间中，$\vec{r}$位置向量以线性动量在 xy 平面中定位粒子$\vec{p}$。相对于原点的角动量为$\vec{l} = \vec{r} \times \vec{p}$，即在 z 方向上。的方向由右手法$\vec{l}$则给出，如图所示。

如固定轴旋转中所述，选择角动量方向垂直于包含$\vec{r}$和$\vec{p}$的平面的意图与选择垂直于$\vec{r}$和$\vec{F}$的平面的扭矩方向类似。角动量的大小是从交叉积的定义中找到的，

\[l = rp \sin \theta,\]

$\vec{r}$和之间的角度在哪里$\theta$$\vec{p}$。角动量的单位为 kg • m ² /s。与扭矩的定义一样，我们可以定义一个杠杆臂$r_\perp$，即从动量向量$\vec{p}$到原点的垂直距离$r_\perp = r \sin \theta$。有了这个定义，角动量的大小变为

\[l = r_{\perp} p = r_{\perp} mv \ldotp\]

我们可以看到，如果的方向$\vec{p}$是通过原点，那么$\theta$ = 0，角动量为零，因为杠杆臂为零。在这方面，角动量的大小取决于原点的选择。如果我们取角动量的时间导数，则得出粒子上扭矩的表达式：

\[ \begin{align*} \frac{d \vec{l}}{dt} &= \frac{d \vec{r}}{dt} \times \vec{p} + \vec{r} \times \frac{d \vec{p}}{dt} \\[4pt] &= \vec{v} \times m \vec{v} + \vec{r} \times \frac{d \vec{p}}{dt} \\[4pt] &= \vec{r} \times \frac{d \vec{p}}{dt} \ldotp \end{align*}\]

这里我们使用了向量$\vec{p}$与自身交叉为零的定义和事实。根据牛顿第二定律$\frac{d \vec{p}}{dt} = \sum \vec{F}$、作用于粒子的净力以及净扭矩的定义，我们可以这样写

\[\frac{d \vec{l}}{dt} = \sum \vec{\tau} \ldotp \label{11.6}\]

注意这与牛顿第二定律的线性结果相似$\frac{d \vec{p}}{dt} = \sum \vec{F}$。以下问题解决策略可以作为计算粒子角动量的指导方针。

问题解决策略：粒子的角动量

选择要计算角动量的坐标系。
用单位向量表示法将半径向量写下点粒子。
用单位向量表示法写入粒子的线性动量矢量。
取十字乘积$\vec{l} = \vec{r} \times \vec{p}$并使用右手定律来确定角动量向量的方向。
查看角动量向量的表达式中是否存在时间依赖性。如果有，则表示原点周围存在扭矩，$\frac{d \vec{l}}{dt} = \sum \vec{\tau}$用于计算扭矩。如果角动量的表达式中没有时间依赖性，则净扭矩为零。

示例$\PageIndex{2}$: Angular Momentum and Torque on a Meteor

流星进入地球大气层（图$\PageIndex{2}$），在流星在大气中燃烧之前被地面上有人观察。矢量$\vec{r}$ = 25 km$\hat{i}$ + 25 km$\hat{j}$ 给出了流星相对于观察者的位置。当观察者看到流星的那一刻，它的线性动量$\vec{p}$ = (15.0 kg) (−2.0 km/s$\hat{j}$)，并且它沿着其路径以恒定的 2.0 m/s ² ($− \hat{j}$) 加速，就我们而言，这可以看作是一条直线。

流星围绕原点（即观察者的位置）的角动量是多少？
流星上关于起源的扭矩是多少？

图中显示了一个 x y 坐标系，正的 x 向右，沿着地面，正的 y 向上。观察者显示在原点附近。矢量 r 显示了从原点到流星的正坐标和正 y 坐标处。流星位置的向量 p 指向下方。 — 图$\PageIndex{2}$：地面上的观察者看到一颗流星处于线$\vec{r}$性动量的位置$\vec{p}$。

策略

我们将加速度解析为 x 和 y 分量，并使用运动学方程将速度表示为加速度和时间的函数。我们将这些表达式插入线性动量中，然后使用交叉积计算角动量。由于位置和动量矢量位于 xy 平面中，因此我们预计角动量矢量将沿 z 轴向量。为了找到扭矩，我们取角动量的时间导数。

解决方案

流星以低于水平线 90.0° 的角度进入地球大气层，因此 x 和 y 方向加速度的分量为

\[a_{x} = 0,\; a_{y} = -2.0\; m/s^{2} \ldotp \nonumber\]

我们使用运动学方程写速度。

\[v_{x} = 0,\; v_{y} = (-2.0 \times 10^{3}\; m/s) - (2.0\; m/s^{2})t \ldotp \nonumber\]

角动量为\[\begin{split} \vec{l} & = \vec{r} \times \vec{p} = (25.0\; km\; \hat{i} + 25.0\; km\; \hat{j}) \times (15.0\; kg)(0 \hat{i} + v_{y} \hat{j}) \\ & = 15.0\; kg [ 25.0\; km (v_{y}) \hat{k}] \\ & = 15.0\; kg \{ (2.50 \times 10^{4}\; m)[(-2.0 \times 10^{3}\; m/s) - (2.0\; m/s^{2})t] \hat{k} \} \ldotp \end{split} \nonumber\] At t = 0，流星围绕原点的角动量是\[\vec{l}_{0} = 15.0\; kg [ (2.50 \times 10^{4}\; m)(-2.0 \times 10^{3}\; m/s) \hat{k}] = 7.50 \times 10^{8}\; kg\; \cdotp m^{2}/s (- \hat{k}) \ldotp \nonumber\]这是观察者看到流星的瞬间。
为了找到扭矩，我们取角动量的时间导数。将时间导数$\vec{l}$作为时间的函数，即紧随其后的第二个方程，我们有\[\frac{d \vec{l}}{dt} = (-15.0\; kg)(2.50 \times 10^{4}\; m)(2.0\; m/s^{2}) \hat{k} \ldotp \nonumber\]那么，因为$\frac{d \vec{l}}{dt} = \sum \vec{\tau}$，我们有\[\sum \vec{\tau} = -7.5 \times 10^{5}\; N\; \cdotp m\; \hat{k} \ldotp \nonumber\]扭矩单位以牛顿米为单位给出，不要与焦耳混淆。作为检查，我们注意到杠杆臂是图$\vec{r}$中向量的 x 分量，$\PageIndex{2}$因为它垂直于作用在流星上的力，流星沿着流星的路径。根据牛顿第二定律，这个力是 $$\ vec {F} = ma (-\ hat {j}) = (15.0\; kg) (2.0\; m/s^ {2}) (-\ hat {j}) = 30.0\; kg\;\ cdotp m/s^ {2} (-\ hat {j})\ ldotp$$杠杆臂是 $$\ vec {r} _ {\ perp} = 2.5\ times 10^ {4}\; m\;\ hat {i}\ ldotp$Thus，扭矩为 $$\ begin {split}\ sum\ vec {r} _ {\ perp}\ times\ vec {F} & = (2.5\ times 10^ {4}\; m\;\ hat {i})\ times (-30.0\; kg\;\ cdotp m/s^ {2}\;\ hat {j})，\\ & = 7.5\ times 10^ {5}\; N\;\ cdotp m (-\ hat {k})\ ldotp\ end {split} $$

意义

由于流星向地球向下加速，因此其半径和速度矢量正在发生变化。因此，从那以后$\vec{l} = \vec{r} \times \vec{p}$，角动量是随时间的变化而变化的。但是，流星绕原点的扭矩是恒定的，因为杠杆臂$\vec{r}_{\perp}$和流星上的力是恒定的。这个例子很重要，因为它说明了角动量取决于计算角动量的原点的选择。本示例中使用的方法对于为粒子系统和刚体生成角动量也很重要。

练习$\PageIndex{1}$

围绕磁场盘旋的质子在纸的平面上执行圆周运动，如下所示。圆形路径的半径为 0.4 m，质子的速度为 4.0 x 10 ⁶ m/s。质子围绕原点的角动量是多少？

质子以逆时针方向移动。圆的半径为 r。质子位于圆心右侧时显示，其速度在向上、正 y 方向上为 v 次垂直。

粒子系统的角动量

粒子系统的角动量在许多科学学科中都很重要，其中一个是天文学。以螺旋星系为例，一个旋转的恒星岛，就像我们自己的银河系一样。单个恒星可以被视为点粒子，每个点粒子都有自己的角动量。单个角力矩的向量和给出了星系的总角动量。在本节中，我们将开发用于计算粒子系统的总角动量的工具。

在上一节中，我们介绍了单个粒子围绕指定原点的角动量。该角动量的表达式为$\vec{l} = \vec{r} \times \vec{p}$，其中向量$\vec{r}$是从原点到粒子，$\vec{p}$是粒子的线性动量。如果我们有一个由$\vec{r}_{i}$ N 个粒子组成的系统，每个粒子都有来自原点的位置向量，每个粒子都有动量$\vec{p}_{i}$，那么围绕原点的粒子系统的总角动量就是围绕原点的单个角力矩的矢量和。也就是说，

\[\vec{L} = \vec{l}_{1} + \vec{l}_{2} + \cdots + \vec{l}_{N} \ldotp \label{11.7}\]

同样，如果粒子 i 受到$\vec{\tau_{i}}$关于原点的净扭矩的影响，那么我们可以通过微分方程 11.7 来找出粒子系统产生的围绕原点的净扭矩：

\[\frac{d \vec{L}}{dt} = \sum_{i} \frac{d \vec{l}_{i}}{dt} = \sum_{i} \tau_{i} \ldotp\]

单个扭矩的总和会在系统上产生净外部扭矩，我们指定该扭矩$\sum \vec{\tau}$。因此，

\[\frac{d \vec{L}}{dt} = \sum_{i} \tau_{i} \ldotp \label{11.8}\]

方程\ ref {11.8} 指出，当两个量相对于给定原点测量时，系统总角动量的变化率等于作用于系统的净外部扭矩。方程\ ref {11.8} 可以应用于任何具有净角动量的系统，包括刚体，如下一节所述。

示例$\PageIndex{2}$: Angular Momentum of Three Particles

参考图$\PageIndex{1a}$：

确定围绕原点的三个粒子产生的总角动量。
角动量的变化率是多少？

显示了 x y 平面中具有不同位置和动量向量的三个粒子。 x 和 y 轴以米为单位显示位置，范围为 -4.0 到 4.0 米。粒子 1 在 x=-2.0 米和 y=1.0 米处，m sub 1 等于 2.0 千克，v sub 1 等于 4.0 j hat meters 每秒，向上 F sub 1 是 -6.0 i hat Newtons。粒子 2 位于 x=4.0 米，y=1.0 米，m sub 2 等于 4.0 千克，v sub 2 等于 5.0 i hat meters，右边 F sub 2 是 10.0 j hat Newtons 向上。粒子 3 位于 x=2.0 米，y=-2.0 米，m sub 3 等于 1.0 千克，v sub 3 等于 3.0 i hat meters，右边 F sub 3 表示向下 -8.0 j hat Newtons。 — 图$\PageIndex{3}$：xy 平面中具有不同位置和动量向量的三个粒子。

策略

写下三个粒子的位置和动量向量。计算单个角力矩并将其作为向量相加，得出总角动量。然后对扭矩做同样的事情。

解决方案

粒子 1：$$\ vec {r} _ {1} = -2.0\; m\;\ hat {i} + 1.0\; m\;\ hat {j},\;\ vec {p} _ {1} = (2.0\; m/s\;\ hat {j}) = 8.0\; kg\;\ cdotp m/s\;\ hat {j}，$$ $$\ vec {l} _ {1} =\ vec {r} _ {1}\ times\ vec {p} _ {1} = -16.0\; kg\;\ cdotp m^ {2} /s\;\ hat {k}\ ldotp$$ Particle 2：$$\ vec {r} _ {2} = 4.0\; m\ hat {i} + 1.0\; m\;\ hat{j},\;\ vec {p} _ {2} = (4.0\; kg) (5.0\; m/s\;\ hat {i}) = 20.0\; kg\;\ cdotp m/s\;\ hat {i}，$$\ vec {l} _ {2} = -20.0\; kg\;\ cdotp m^ {2} /s\;\ hat {k}\ ldotp$Particle 3: $$\ vec {r} _ {3} = 2.0\; m\;\ hat {j},\;\ vec {p} _ {3} = (1.0\; kg) (3.0\; m/s\;\ hat {i}) = 3.0\; kg\;\ cdotp m/s\;\ hat {j}，$$\ vec {l} _ {3} =\ vec {r} _ {3}\ times\ vec {p} _ {3} = 6.0\; kg\;\ cdotp m^ {2} /s\;\ hat {k}\ ldotp$我们添加单个角力矩来得出原点的总数：$$\ vec {l} _ {T} =\ vec {l} _ {1} +\ vec {l} _ {2} +\ vec {l} _ {3} = -30\; kg\;\ cdotp m^ {2} /s\;\ hat {k}\ ldotp$$
单个力量和杠杆臂为 $$\ begin {split}\ vec {r} _ {1\ perp} & = 1.0\; m\;\ hat {j},\;\ vec {F} _ {1} = 6.0\;\ vec {\ tau} = 6.0\;\ cdotp m\; hat {k}\\ vec {r} _ {2\ perp} & = 4.0\; m\;\ hat {i},\;\ vec {F} _ {2} = 10.0\;\ hat {i},\;\ vec {\ tau} _ {2} = 40.0\; N\;\ cdotp m\;\hat {k}\\ vec {r} _ {3\ perp} & = 2.0\; m\;\ hat {j},\;\ vec {F} _ {3} = -8.0\;\ hat {j},\;\ vec {\ tau} _ {3} = -16.0\; N\;\ cdotp m\;\ hat {k} dotp\ end {split} $$因此：$$\ sum_ {i}\ vec {\ tau} _ {i} =\ vec {\ tau} _ {1} +\ vec {\ tau} _ {3} = 30\; N\;\ cdotp m\;\ hat {k}\ ldotp$$

意义

这个例子说明了粒子系统的角动量和扭矩的叠加原理。在计算粒子的半径向量$\vec{r}_{i}$以计算角力矩时必须小心，评估杠杆臂计算扭矩时必须小心，因为它们的量完全不同。$\vec{r}_{i \perp}$

刚体的角动量

我们已经研究了单个粒子的角动量，并将其概括为粒子系统。现在，我们可以使用上一节中讨论的原理来开发刚体角动量的概念。诸如行星之类的天体由于自旋和绕恒星运行而具有角动量。在工程中，任何绕轴旋转的东西都带有角动量，例如飞轮、螺旋桨和发动机中的旋转部件。了解这些物体的角力矩对于设计它们所处的系统至关重要。

为了开发刚体的角动量，我们将刚体建模为由小质量段$\Delta$ m _i 组成的刚体。在图中$\PageIndex{4}$，刚体被限制为围绕 z 轴以角速度旋转$\omega$。构成刚体的所有质量段都以相同的角速度绕 z 轴进行圆周运动。图 (a) 部分显示了质量段$\Delta$ m _i，其位置向量是$\vec{r}_{i}$从原点和半径 R _i 到 z 轴。其切向速度的大小为 v _i = R _i$\omega$。由于向量$\vec{v}_{i}$和$\vec{r}_{i}$相互垂直，因此该质量分段的角动量的大小为

\[l_{i} = r_{i} (\Delta mv_{i}) \sin 90^{o} \ldotp\]

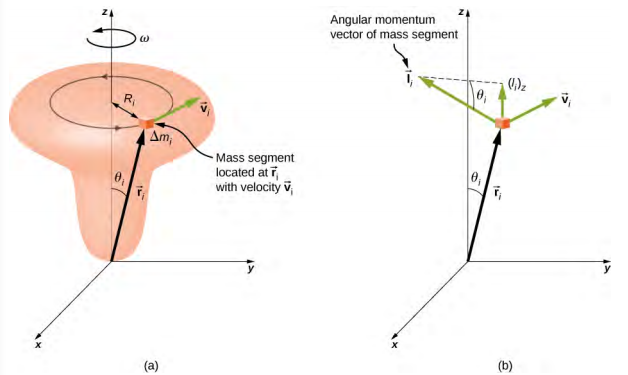
图 a 显示了门把手形状的物体和 x y z 坐标系。物体垂直排列，以 z 轴为中心，宽旋钮位于顶部。物体围绕 z 轴旋转，从上方看，逆时针旋转，角速度为 omega。对象的一小部分被突出显示。这个标有 Delta m sub i 的质量分段位于向量 r sub i 处，与速度向量 v sub i 一起移动，沿逆时针方向追踪半径为 R sub i 的圆。向量 r sub i 从原点延伸到质量段，与 z 轴成一个 theta sub i 的角度。向量 v sub i 与质量段所描绘的圆相切。图 b 显示了 x y 坐标系和质量段。再次显示向量 r sub i 和 v sub i，矢量 r sub i 和 z 轴之间的角度 theta sub i 也是如此。还显示了质量分段的角动量矢量，即向量 l sub i。向量 l sub i 垂直于 r 和 v，如右手法则所示，并具有向上的 z 分量，如图所示，标为 l sub i z。直角三角形的剩余边为 l sub i z，其斜边为 l sub i z，显示为虚线。与这边相邻且与垂直边 l sub i z 相反的角度为 theta sub i。 — 图$\PageIndex{4}$：(a) 刚体受限围绕 z 轴旋转。刚体围绕 z 轴对称。质量段$\Delta$ m _i 位于相应位置$\vec{r}_{i}$，该位置$\theta_{i}$与 z 轴形成角度。显示了无穷小质量段的圆周运动。 (b)$\vec{l}_{i}$ 是质量段的角动量，具有沿 z 轴 ($\vec{l}_{i}$) _z 的分量。

使用右手法则，角动量矢量指向图中所示的方向$\PageIndex{4b}$。所有质量段的角力矩之和包含沿旋转轴和垂直于旋转轴的分量。每个质量段都有角动量的垂直分量，该分量将被刚体另一侧相同质量段的垂直分量所抵消。因此，沿旋转轴的分量是唯一在将所有质量段相加时得出非零值的分量。从 (b) 部分开始，$\vec{l}_{i}$沿旋转轴的分量为

\[\begin{split} (l_{i})_{z} & = l_{i} \sin \theta_{i} = (r_{i} \Delta m_{i} v_{i}) \sin \theta_{i}, \\ & = (r_{i} \sin \theta_{i})(\Delta m_{i} v_{i}) = R_{i} \Delta m_{i} v_{i} \ldotp \end{split}\]

刚体沿旋转轴的净角动量为

\[L = \sum_{i} (\vec{l}_{i})_{z} = \sum_{i} R_{i} \Delta m_{i} v_{i} = \sum_{i} R_{i} \Delta m_{i} (R_{i} \omega) = \omega \sum_{i} \Delta m_{i} (R_{i})^{2} \ldotp\]

求和$\sum_{i} \Delta$ (R _i) ² 就是刚体绕旋转轴的惯性矩 I。对于围绕垂直于圈形平面的轴线旋转的细圈，所有 R _i 都等于 R，因此求和减小为 R ²$\sum_{i} \Delta$ m _i = mR ²，这是图 10.20 中找到的细圈的惯性矩。因此，沿着以角速度$\omega$绕轴旋转的刚体的旋转轴的角动量的大小为

\[L = I \omega \ldotp \label{11.9}\]

该方程类似于线性动量 p = mv 的大小。角动量向量的方向沿着右手法则给出的旋转轴指向。

示例$\PageIndex{3}$: Angular Momentum of a Robot Arm

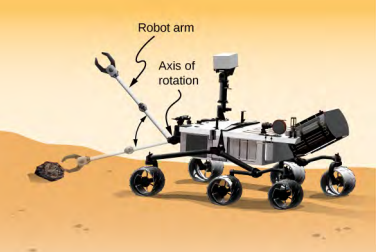
像图$\PageIndex{5}$中所示的好奇号这样的火星探测器上的机器人手臂长 1.0 m，自由端有镊子可以捡起石头。手臂的重量为2.0 kg，钳子的质量为1.0 kg（图$\PageIndex{5}$）。机器人手臂和钳子在 0.1 秒内从静止位置移动到$\omega$ = 0.1$\pi$ rad/s。它向下旋转并捡起质量为 1.5 kg 的火星岩石。旋转轴是机器人手臂连接到漫游者的点。

当手臂停止加速时，0.1 秒后，机器人手臂本身围绕旋转轴的角动量是多少？
当机器人手臂的钳子里有火星岩石并且向上旋转时，它的角动量是多少？
当手臂的镊子里没有石头时，当漫游者从静止状态加速到最终角速度时，手臂与漫游车相连的扭矩是多少？

火星探测器的插图。末端有爪子的手臂从漫游者的一端延伸，可以上下旋转以捡起石头。旋转轴是机器人手臂连接到漫游者的点。 — 图$\PageIndex{5}$：火星探测器上的机器人手臂向下摆动并捡起一块火星岩石。（来源：美国航空航天局/JPL-CalTech 对作品的修改）

策略

我们使用方程\ ref {11.9} 来查找各种配置中的角动量。当手臂向下旋转时，右手定律给出了指向页面的角动量向量，我们称之为正 z 方向。当手臂向上旋转时，右手定律给出角动量向量进入页面的方向或朝负 z 方向的方向。惯性矩是各个惯性矩的总和。手臂可以用实心棒近似，镊子和火星岩石可以近似为距离原点 1 m 的点质量。对于 (c) 部分，我们使用牛顿第二运动定律进行旋转，以找到机器人手臂上的扭矩。

解决方案

写下个别的惯性矩，我们有

机器人手臂：\[I_{R} = \frac{1}{3} m_{R} r^{2} = \frac{1}{3} (2.00\; kg)(1.00\; m)^{2} = \frac{2}{3}\; kg\; \cdotp m^{2} \ldotp\]
镊子：\[I_{F} = m_{F} r^{2} = (1.0\; kg)(1.0\; m)^{2} = 1.0\; kg\; \cdotp m^{2} \ldotp\]
火星摇滚：\[I_{MR} = m_{MR} r^{2} = (1.5\; kg)(1.0\; m)^{2} = 1.5\; kg\; \cdotp m^{2} \ldotp\]

因此，如果没有火星岩石，总惯性矩为

\[I_{Total} = I_{R} + I_{F} = 1.67\; kg\; \cdotp m^{2}\]

角动量的大小为

\[L = I \omega = (1.67\; kg\; \cdotp m^{2})(0.1 \pi\; rad/s) = 0.17 \pi\; kg\; \cdotp m^{2}/s \ldotp\]

由于机器人手臂逆时针旋转，因此角动量$\hat{k}$向量被引导出页面。

我们必须将火星岩石包括在惯性矩的计算中，所以我们有\[I_{Total} = I_{R} + I_{F} + I_{MR} = 3.17\; kg\; \cdotp m^{2}\]了，\[L = I \omega = (3.17\; kg\; \cdotp m^{2})(0.1 \pi\; rad/s) = 0.32 \pi\; kg\; \cdotp m^{2}/s \ldotp\]现在角动量向量按照右手法则指向页面$− \hat{k}$的方向，因为机器人手臂现在正在顺时针旋转。
我们通过使用方程\ ref {11.8} 取角动量的导数来计算手臂没有岩石时的扭矩$\frac{d \vec{L}}{dt} = \sum \vec{\tau}$。但是由于 L = I$\omega$，并且理解角动量和扭矩向量的方向是沿着旋转轴的方向，我们可以抑制向量表示法，找出\[\frac{dL}{dt} = \frac{d (I \omega)}{dt} = I \frac{d \omega}{dt} = I \alpha = \sum \tau,\]哪个是牛顿的第二旋转定律。因为$\alpha = \frac{0.1 \pi\; rad/s}{0.1\; s} = \pi\; rad/s^{2}$，我们可以计算净扭矩：\[\sum \tau = I \alpha = (1.67\; kg\; \cdotp m^{2})(\pi\; rad/s^{2}) = 1.67 \pi\; N\; \cdotp m \ldotp\]

意义

(a) 中的角动量小于 (b) 中的角动量，因为 (b) 中的惯性矩大于 (a)，而角速度相同。

练习$\PageIndex{3}$

哪个具有更大的角动量：质球 m 围绕 z 轴以恒定角频率$\omega_{0}$旋转，还是围绕 z 轴具有相同质量和旋转速率的实心圆柱体？

模拟

访问科罗拉多大学的角动量交互式模拟，了解有关角动量的更多信息。

粒子的角动量

问题解决策略：粒子的角动量

示例\(\PageIndex{2}\): Angular Momentum and Torque on a Meteor

解决方案

练习\(\PageIndex{1}\)

示例\(\PageIndex{2}\): Angular Momentum of Three Particles

解决方案

示例\(\PageIndex{3}\): Angular Momentum of a Robot Arm

解决方案

练习\(\PageIndex{3}\)

模拟