Skip to main content
Global

11.2: 滚动动作

  1. Last updated
  2. Save as PDF
  • Page ID
    204355

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标
    • 描述不滑动的滚动运动的物理原理
    • 解释在没有滑动的情况下滚动运动中，线性变量与角度变量有何关系
    • 找出有或没有滑动的滚动运动中的线性加速度和角加速度
    • 计算与无滑动的滚动运动相关的静摩擦力
    • 利用节能分析滚动运动

    滚动运动是我们每天到处都能看到的旋转和平移运动的常见组合。 想想车轮在高速公路上移动，飞机上的轮子降落在跑道上，或者机器人探险家上的轮子在另一个星球上移动的不同情况。 了解滚动运动所涉及的力和扭矩是许多不同类型情况下的关键因素。

    要分析本章中的滚动运动，请参阅固定轴旋转中的图 10.5.4 以找出一些常见几何物体的惯性矩。 你可能还会发现它在涉及旋转的其他计算中很有用。

    滚动动作不会滑动

    自车轮发明以来，人们就一直观察到滚动运动，没有滑动。 例如，我们可以看一下汽车轮胎和路面的相互作用。 如果驾驶员将油门压到地板上，使轮胎在没有汽车向前移动的情况下旋转，则车轮和路面之间必须存在动摩擦。 如果驾驶员缓慢地按下油门，导致汽车向前移动，则轮胎会滚动而不会打滑。 令大多数人感到惊讶的是，事实上，车轮底部相对于地面处于静止状态，这表明轮胎和路面之间肯定存在静摩擦。 在图中\(\PageIndex{1}\)，自行车处于运动状态，骑手保持直立。 轮胎会与路面接触，尽管它们在滚动，但轮胎底部会稍微变形，不会打滑，并且相对于路面在可测量的时间内处于静止状态。 轮胎和路面之间必须有静摩擦才能做到这一点。

    图 a 是一张骑自行车的人的照片。 摄像头跟随自行车，因此自行车和骑手的图像非常清晰，由于自行车的运动，背景变得模糊。 图 b 是一张自行车车轮在地面上滚动、相机相对于地面静止的照片。 车轮和轮辐顶部模糊，但底部清晰。
    图\(\PageIndex{1}\)：（a）自行车向前移动，轮胎不会打滑。 稍微变形的轮胎底部相对于路面静止了一段可测量的时间。 (b) 这张图显示滚轮的顶部因其运动而显得模糊，但滚轮的底部瞬间处于静止状态。 （来源 a：纳尔逊·洛伦索对作品的修改；来源 b：科林·罗斯对作品的修改）

    为了分析无滑动的滚动，我们首先根据描述车轮运动的角度变量推导出车轮质心速度和加速度的线性变量。 情况如图所示\(\PageIndex{2}\)。

    图 a 显示了车轮的自由车身图，包括力作用的位置。 显示了四种力：M g 是作用在车轮中心的向下力。 N 是作用于车轮底部的向上力。 F 是向右的力，作用在车轮的中心，f sub s 是作用在车轮底部的左侧力。 f sub s 的力小于或等于 mu sub s 乘以 N。图 b 是车轮在水平表面上滚动而不滑动的示意图。 点 P 是车轮底部和表面之间的接触点。 轮子顺时针旋转，sub C M 右侧有加速度，v sub V M 右侧有速度。给出了 omega 等于 v sub C M 比 R 的关系，alpha 等于 R 之上的子 C M。 显示了一个坐标系，其右侧为正 x，正向上 y。 图 c 显示了质心框架中的轮子。 点 P 的速度矢量相对于车轮的质心处于负方向。 该向量显示在图中，标记为减去 R omega i hat。 它与底部的轮子相切，指向左边。 显示了车轮边缘不同位置的附加向量，所有向量都与车轮相切并指向顺时针。
    图\(\PageIndex{2}\)：(a) 轮子被力拉过水平表面\(\vec{F}\)。 静摩擦力\(|\vec{f}_{s}|\) ≤\(\mu_{s}\) N 足够大\(\vec{f}_{s}\)，足以防止其滑动。 (b) 质心的线性速度和加速度矢量以及和的相关表达式\(\alpha\)。\(\omega\) 点 P 相对于表面处于静止状态。 (c) 相对于质心 (CM) 框架，点 P 的线性速度 −R\(\omega \hat{i}\)。

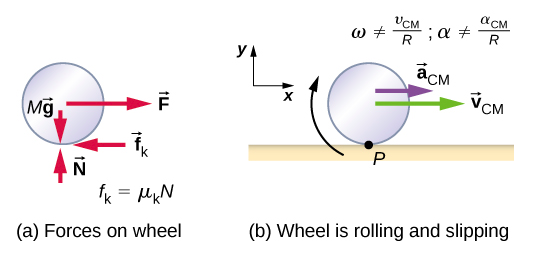
    从图\(\PageIndex{2}\) (a) 中，我们可以看到防止车轮滑动所涉及的力向量。 在 (b) 中，接触表面的点 P 相对于表面处于静止状态。 相对于质心，点 P 的速度 −R\(\omega \hat{i}\)，其中 R 是轮子的半径，\(\omega\)是轮子绕其轴线的角速度。 由于轮子在滚动，P 相对于表面的速度是其相对于质心的速度加上质心相对于表面的速度：

    \[\vec{v}_{P} = -R \omega \hat{i} + v_{CM} \hat{i} \ldotp\]

    由于 P 相对于表面的速度为零，v P = 0，这说明了

    \[v_{CM} = R \omega \ldotp \label{11.1}\]

    因此，车轮质心的速度等于其半径乘以绕其轴线的角速度。 我们显示了方程左侧的线性变量与方程右侧的角度变量的对应关系。 线性加速度如下所示。

    如果我们区分方程左侧的方程\ ref {11.1}，则得到质心线性加速度的表达式。 在方程的右边，R 是一个常数，由于\(\alpha = \frac{d \omega}{dt}\)，我们有

    \[a_{CM} = R \alpha \ldotp \label{11.2}\]

    此外，我们可以参考图，根据角度变量找到车轮的行进距离\(\PageIndex{3}\)。 当车轮从 A 点滚动到 B 点时，其外表面正好按照行进距离（即 d CM）映射到地面。

    从图中我们可以看出\(\PageIndex{3}\)，映射到地面的外表面的长度是弧长 R\(\theta\)。 等同于两个距离，我们得到

    \[d_{CM} = R \theta \ldotp \label{11.3}\]

    半径为 R 的轮子在水平表面上滚动，在 v sub C M 处向右移动，在两个位置上绘制。 在第一个位置，车轮上的点 A 位于底部，与表面接触，点 B 位于顶部。 沿车轮轮缘从 A 到 B 的弧长被突出显示并标记为 R theta。 在第二个位置，车轮上的点 B 位于底部，与表面接触，点 A 位于顶部。 在图示的两个位置上，车轮与表面接触点之间的水平距离为 d sub C M。弧长 A B 现在位于车轮的另一侧。
    图\(\PageIndex{3}\)：当轮在表面上滚动时，\(\theta\)从 A 到 B 的弧长 R 映射到曲面上，对应于质心移动的距离 d CM。
    示例\(\PageIndex{1}\): Rolling Down an Inclined Plane

    从静止开始，坚固的圆柱体在倾斜的平面上滚动而不会滑动。 它的质量为 m，半径为 r。（a）它的加速度是多少？ (b) 静摩擦系数必须\(\mu_{S}\)满足什么条件才能使气缸不会打滑？

    策略

    绘制草图和自由体图，然后选择坐标系。 我们将 x 放置在平面下方的方向上，将 y 朝上垂直于平面。 确定所涉及的部队。 它们是法向力、重力和摩擦产生的力。 写下 x 和 y 方向上的牛顿定律和牛顿旋转定律，然后求解摩擦产生的加速度和力。

    解决方案
    1. 自由体图和草图如图所示\(\PageIndex{4}\)，包括法向力、重量分量和静摩擦力。 几乎没有足够的摩擦力来保持气缸滚动而不会滑动。 由于没有滑动，摩擦力的大小小于或等于\(\mu_{S}\) N 写下 x 和 y 方向上的牛顿定律，我们有

    \[\sum F_{x} = ma_{x};\; \sum F_{y} = ma_{y} \ldotp\]

    圆柱体在不滑下倾斜平面的情况下滚动的示意图和气缸的自由体图。 左边是显示倾斜平面的插图，该平面与水平方向成了 theta 的角度。 显示气缸在顶部处于静止状态，然后在较低时沿着斜坡移动。 右边是免费的人体图。 x y 坐标系倾斜，使得正 x 方向平行于倾斜平面并指向其底部，正的 y 方向向向向外，垂直于平面。 图中显示了四种力。 N j hat 作用在圆柱体的中心并指向正 y 方向。m g sine theta i hat 作用于圆柱体的中心，指向正 x 方向。 减去 m g cosine theta j hat 作用于圆柱体的中心，指向负 y 方向。 减去 f sub s i hat 在接触点起作用，指向负 x 方向。
    图\(\PageIndex{4}\)：坚固的圆柱体在倾斜的平面上滚动，不会从静止处滑落。 坐标系有 x 在倾斜平面下方向，y 垂直于平面。 自由体图显示了法向力、静摩擦力和重量 m 的分量\(\vec{g}\)。 摩擦使气缸从飞机上滚下来而不是滑动。

    从自由体图中替换

    \[\begin{split} mg \sin \theta - f_{s} & = m(a_{CM}) x, \\ N - mg \cos \theta & = 0 \end{split}\]

    然后我们可以根据以下方程求解质心的线性加速度：

    \[a_{CM} = g\sin \theta - \frac{f_s}{m} \ldotp\]

    但是，用惯性矩来表示线性加速度很有用。 为此，我们写下牛顿的第二旋转定律，

    \[\sum \tau_{CM} = I_{CM} \alpha \ldotp\]

    扭矩是围绕轴线通过圆柱体质心计算的。 唯一的非零扭矩由摩擦力提供。 我们有

    \[f_{s} r = I_{CM} \alpha \ldotp\]

    最后，线性加速度与角加速度有关

    \[(a_{CM})_{x} = r \alpha \ldotp\]

    这些方程可以用来根据惯性矩求解 CM\(\alpha\)、和 f S，我们删除了 x 下标。 我们用重力的垂直分量和摩擦力写一个 CM，然后进行以下替换。

    \[f_{S} = \frac{I_{CM} \alpha}{r} = \frac{I_{CM} a_{CM}}{r^{2}}\]

    由此我们得到

    \[\begin{split} a_{CM} & = g \sin \theta - \frac{I_{CM} a_{CM}}{mr^{2}}, \\ & = \frac{mg \sin \theta}{m + \left(\dfrac{I_{CM}}{r^{2}}\right)} \ldotp \end{split}\]

    请注意，此结果与静摩擦系数无关\(\mu_{s}\)。

    由于我们有一个实心圆柱体，从图 10.5.4 来看，我们有 I CM =\(\frac{mr^{2}}{2}\) 和

    \[a_{CM} = \frac{mg \sin \theta}{m + \left(\dfrac{mr^{2}}{2r^{2}}\right)} = \frac{2}{3} g \sin \theta \ldotp\]

    因此，我们有

    \[\alpha = \frac{a_{CM}}{r} = \frac{2}{3r} g \sin \theta \ldotp\]

    1. 因为不会发生滑动，f S ≤\(\mu_{s}\) N 求解摩擦力，$$f_ {s} = I_ {CM}\ frac {\ alpha} {r} = I_ {CM}\ frac {(a_ {CM})} {r^ {2}} {r^ {CM}} {r^ {2}}\ 左 (\ dfrac c {mg\ sin\ theta} {m +\ 左 (\ dfrac {I_ {CM}} {r^ {2}}\ 右)}\ 右) =\ frac {mg I_ {CM}\ sin\ theta} {mr^ {2}+ I_ {CM}}\ ldotp$$用这个表达式替换为不滑动的条件，注意 N = mg cos\(\theta\)，我们有 $$\ frac {mg I_ {CM}\ sin\ theta} {mr^ {2} + I_ {s} mg\ cos\ theta$or $$\ mu_ {s}\ geq frac {\ tan\ theta} {1 +\ 左 (\ dfrac {mr^ {2}} {I_ {CM}}\ 右)}\ ldotp$for solid气缸，这变成了 $$\ mu_ {s}\ geq\ frac {\ tan\ theta} {1 +\ 左 (\ dfrac {2mr^ {2}} {mr^ {2}}\ 右)} =\ frac {1} {3}\ tan\ theta\ ldotp$$

    意义

    1. 线性加速度与 sin 成线性成正比\(\theta\)。 因此，正如预期的那样，倾斜角度越大，线性加速度就越大。 但是，角加速度与正弦成线性成正比，与圆柱体的半径成反比。\(\theta\) 因此，半径越大，角加速度越小。
    2. 为了不发生滑动，静摩擦系数必须大于或等于\(\frac{1}{3}\)棕褐色\(\theta\)。 因此，倾斜角度越大，静摩擦系数必须越大，以防止气缸滑动。
    练习\(\PageIndex{2}\)

    空心圆柱以 60° 的角度在斜面上。 表面的静摩擦系数为\(\mu_{s}\) = 0.6。 (a) 气缸滚动时不打滑吗？ (b) 坚固的气缸能否滚动而不打滑？

    值得重复本示例中得出的加速物体滚动而不滑动的方程：

    \[a_{CM} = \frac{mg \sin \theta}{m + \left(\dfrac{I_{CM}}{r^{2}}\right)} \ldotp \label{11.4}\]

    这是一个非常有用的方程式，用于解决涉及滚动而不打滑的问题。 请注意，加速度小于在无摩擦平面上滑动而不旋转的物体的加速度。 对于具有不同旋转惯性的两个旋转气缸，加速度也会有所不同。

    滑动时的滚动动作

    在带有滑动的滚动运动中，我们必须使用动摩擦系数，由于不存在静摩擦，动摩擦系数会产生动摩擦力。 情况如图所示\(\PageIndex{5}\)。 在滑动的情况下，v CM − R\(\omega\) ≤ 0，因为车轮上的点 P 在表面上没有静止状态，v P ≤ 0。 因此，\(\omega\)≤\(\frac{v_{CM}}{R}\)，\(\alpha \neq \frac{a_{CM}}{R}\)。

    图 a 显示了车轮的自由车身图，包括力作用的位置。 显示了四种力：M g 是作用在车轮中心的向下力。 N 是作用于车轮底部的向上力。 F 是向右的力，作用在车轮的中心，f sub k 是作用在车轮底部的左侧力。 力 f sub k 等于 mu sub k 乘以 N。图 b 是车轮在水平表面上滚动和滑动的示意图。 轮子顺时针旋转，sub C M 右侧有加速度，v sub V M 右侧有速度。omega 不等于 r 上的 v sub C M，alpha 不等于 R 上的 sub C M。如图所示坐标系右侧为正 x，正向上 y。
    图\(\PageIndex{5}\)：(a) 由于车轮打滑，车轮和表面之间会产生动摩擦。 (b) 线性变量和角度变量之间的简单关系不再有效。
    示例\(\PageIndex{2}\): Rolling Down an Inclined Plane with Slipping

    实心圆柱体从静止处向下滚动倾斜的平面并发生滑动（图\(\PageIndex{6}\)）。 它的质量为 m，半径为 r。（a）它的线性加速度是多少？ (b) 它绕穿过质心的轴线的角加速度是多少？

    策略

    绘制草图和自由体图，显示所涉及的力。 自由体图与防滑情况类似，但摩擦力除外，摩擦力是动态的，而不是静态的。 使用牛顿第二定律求解 x 方向上的加速度。 使用牛顿第二旋转定律求解角加速度。

    解决方案
    圆柱体在倾斜平面上滚动和滑动的示意图和圆柱体的自由体图。 左边是显示倾斜平面的插图，该平面与水平方向成了 theta 的角度。 显示气缸在顶部处于静止状态，然后在较低时沿着斜坡移动。 右边是免费的人体图。 x y 坐标系倾斜，使得正 x 方向平行于倾斜平面并指向其底部，正的 y 方向向向向外，垂直于平面。 图中显示了四种力。 N j hat 作用在圆柱体的中心并指向正 y 方向。m g sine theta i hat 作用于圆柱体的中心，指向正 x 方向。 减去 m g cosine theta j hat 作用于圆柱体的中心，指向负 y 方向。 减去 f sub k i hat 在接触点起作用，指向负 x 方向。
    图\(\PageIndex{6}\)：实心圆柱体从静止处向下滚动倾斜的平面并发生滑动。 坐标系有 x 沿着倾斜平面向下的方向，y 向上垂直于该平面。 自由体图显示了法向力、动摩擦力和重量 m 的分量\(\vec{g}\)。

    y 方向上的力之和为零，因此摩擦力现在为 f k =\(\mu_{k}\) N =\(\mu_{k}\) mg cos\(\theta\)。 牛顿在 x 方向上的第二定律变成

    \[\sum F_{x} = ma_{x}, \nonumber\]

    \[mg \sin \theta - \mu_{k} mg \cos \theta = m(a_{CM})_{x}, \nonumber\]

    要么

    \[(a_{CM})_{x} = g(\sin \theta - \mu_{k} \cos \theta) \ldotp \nonumber\]

    摩擦力提供绕轴线穿过质心的唯一扭矩，因此牛顿的第二旋转定律变成

    \[\sum \tau_{CM} = I_{CM} \alpha, \nonumber\]

    \[f_{k} r = I_{CM} \alpha = \frac{1}{2} mr^{2} \alpha \ldotp \nonumber\]

    求解\(\alpha\)，我们有

    \[\alpha = \frac{2f_{k}}{mr} = \frac{2 \mu_{k} g \cos \theta}{r} \ldotp \nonumber\]

    意义

    我们用动摩擦系数来写线性和角加速度。 线性加速度与物体在动摩擦下倾斜平面上滑动时所得的线性加速度相同。 围绕旋转轴的角加速度与法向力成线性成正比，法向力取决于倾角的余弦值。 当\(\theta\) → 90° 时，该力变为零，因此，角加速度变为零。

    滚动运动中的机械能守恒

    在上一章中，我们介绍了旋转动能。 任何滚动物体都携带旋转动能，如果系统需要，还会携带平移动能和势能。 包括引力势能，物体滚动的总机械能为

    \[E_{T} = \frac{1}{2} mv^{2}_{CM} + \frac{1}{2} I_{CM} \omega^{2} + mgh \ldotp\]

    在没有任何非保守力量以热量的形式从系统中吸收能量的情况下，滚动物体不会滑动的总能量是保守的，并且在整个运动过程中保持不变。 能量不守恒的例子包括滚动物体滑动、动摩擦产生的热量以及遇到空气阻力的滚动物体。

    你可能会问，为什么没有滑动的滚动物体会节省能量，因为静摩擦力是不保守的。 可以通过参考图找到答案\(\PageIndex{2}\)。 与表面接触的点 P 相对于表面处于静止状态。 因此，它\(\vec{r}\)相对于表面的无穷小位移 d 为零，静摩擦力所做的增量功率为零。 我们可以将节能应用到滚动运动的研究中，得出一些有趣的结果。

    示例\(\PageIndex{3}\): Curiosity Rover

    如图\(\PageIndex{7}\)所示，好奇号探测器于 2012 年 8 月 6 日部署在火星上。 漫游者的车轮半径为25厘米。 假设宇航员在2050年抵达火星，在盆地旁发现了现在无法运作的好奇号。 当他们拆除漫游车时，一名宇航员不小心失去了对其中一个轮子的抓地力，该轮子在滚动时没有滑入25米以下的盆底。 如果轮子的质量为5 kg，那么它在盆底的速度是多少？

    美国宇航局好奇号探测器在喷气推进实验室进行测试期间的照片。
    图\(\PageIndex{7}\)：美国宇航局火星科学实验室探测器 “好奇号” 在 2011 年 6 月 3 日测试期间。 该地点位于加利福尼亚州帕萨迪纳的美国宇航局喷气推进实验室的航天器装配设施内。 （来源：NASA/JPL-CalTech）

    策略

    我们使用机械节能来分析问题。 在山顶，车轮处于静止状态，只有潜在的能量。 在盆地底部，车轮具有旋转和平移动能，必须等于通过节能产生的初始势能。 由于车轮在滚动时不会滑动，因此我们使用关系 v CM = r\(\omega\) 将平移变量与节能方程中的旋转变量关联起来。 然后我们求解速度。 从图\(\PageIndex{7}\)中我们可以看出，空心圆柱是车轮的近似值，因此我们可以使用这个惯性矩来简化计算。

    解决方案

    盆地顶部的能量等于底部的能量：

    \[mgh = \frac{1}{2} mv_{CM}^{2} + \frac{1}{2} I_{CM} \omega^{2} \ldotp \nonumber\]

    已知数量为 I CM = m r 2、r = 0.25 m 和 h = 25.0 m。

    我们使用\(\omega\) = v CM r 重写节能方程消除\(\omega\)。我们有

    \[mgh = \frac{1}{2} mv_{CM}^{2} + \frac{1}{2} mr^{2} \frac{v_{CM}^{2}}{r^{2}} \nonumber\]

    要么

    \[gh = \frac{1}{2} v_{CM}^{2} + \frac{1}{2} v_{CM}^{2} \Rightarrow v_{CM} = \sqrt{gh} \ldotp \nonumber\]

    在火星上，重力加速度为3.71 m/s 2，这使得盆地底部的速度大小为

    \[v_{CM} = \sqrt{(3.71\; m/s^{2})(25.0\; m)} = 9.63\; m/s \ldotp \nonumber\]

    意义

    考虑到火星的大气层很少，而且空气阻力造成的能量损失微乎其微，这是一个相当准确的结果。 结果还假设地形平滑，因此车轮在途中不会遇到岩石和颠簸。

    此外，在本例中，动能或运动能量在线性运动和旋转运动之间平均分配。 如果我们看一下图 10.5.4 中的惯性矩，就会发现空心圆柱在给定半径和质量下具有最大的惯性矩。 例如，如果漫游者的车轮是坚固的，并且由实心圆柱体近似，那么线性运动中的动能将比旋转运动中的动能更多。 这将使轮子的线性速度大于空心圆柱近似值。 因此，实心圆柱体到达水槽底部的速度比空心圆柱体快。