5.8: 绘制自由体图

Last updated
Save as PDF

Page ID: 205006

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

解释绘制自由体图的规则
针对不同情况绘制自由体图

描述和分析物理学中大多数现象的第一步是仔细绘制自由体图。本章的示例中都使用了自由体图。请记住，自由体图只能包括作用于目标主体的外力。一旦我们绘制了精确的自由体图，如果身体处于平衡状态（即平衡力；也就是说\(F_{net} = 0\)），我们可以应用牛顿的第一定律；如果身体正在加速（不平衡力；也就是说，\(F_{net} \neq 0\)），我们可以应用牛顿第二定律。

在 F or ces 中，我们给出了简短的问题解决策略，以帮助您理解自由体图。在这里，我们在策略中添加了一些细节，这些细节将帮助您构建这些图表。

问题解决策略：构建自由体图

构造自由体图时，请遵守以下规则：

画出正在考虑的物体；它不一定是艺术性的。首先，你可能需要在感兴趣的物体周围画一个圆圈，以确保你专注于标记作用在物体上的力。如果您将物体视为粒子（没有大小或形状，也没有旋转），请将该对象表示为一个点。我们经常将这个点放在 xy 坐标系的原点。
包括作用于物体的所有力，将这些力表示为向量。考虑 Comm on Forces 中描述的力类型（法向力、摩擦力、张力和弹簧力）以及重量和施加力。不要在物体上施加净力。除了重力之外，我们讨论的所有力都需要与物体直接接触。但是，不得将物体对其环境施加的力包括在内。我们从不包括动作-反应对中的两种力量。
将自由体图转换为更详细的图，显示给定力的 x 和 y 分量（这在使用牛顿第一定律或第二定律求解问题时通常很有用）。在这种情况下，在原始向量上放置一条波浪线，以表明它不再在玩——它已被其 x 和 y 分量所取代。
如果问题中有两个或更多物体或主体，请为每个对象绘制单独的自由体图。

注意：如果存在加速度，我们不会将其直接包含在自由体图中；但是，在自由体图之外表示加速度可能会有所帮助。您可以用不同的颜色对其进行标记，以表明它与自由体图是分开的。

让我们在绘制雪橇的自由体图时运用问题解决策略。在图中\(\PageIndex{1a}\)，雪橇是用力\(\vec{P}\)以 30° 的角度拉动的。在 (b) 部分中，我们展示了这种情况的自由体图，如问题解决策略的步骤 1 和 2 所述。在 (c) 部分中，我们按照步骤 3 显示所有力，以 x 和 y 分量表示。

图 a 显示了 15 千克的雪橇。标有 P 的箭头指向右和向上，与水平方向成为 30 度的角度。图 b 是自由体图，P，N 指向上方，w 指向下。图 c 是一个自由体图，其中 P、N、w 和 P 的两个分量：Px 指向右，Py 指向上方。 — 图\(\PageIndex{1}\)：(a) 移动雪橇显示为 (b) 自由体图和 (c) 包含力分量的自由体图。

示例\(\PageIndex{1}\): Two Blocks on an Inclined Plane

构造图中对象 A 和对象 B 的自由体图\(\PageIndex{1}\)。

策略

我们遵循问题解决策略中列出的四个步骤。

解决方案

我们首先为第一个感兴趣的对象创建一个图表。在图中\(\PageIndex{2a}\)，对象 A 被隔离（圈出）并用点表示。

图 a 显示了倾斜平面上的两个物体，向左倾斜。对象 A 位于对象 B 的顶部。自由体图显示 T 指向右和向上，平行于平面，N 下标 BA 指向左和向上，垂直于平面，f 下标 BA 指向左和向下，平行于平面，w 下标 A 指向垂直向下。 W 下标 A 是方块 A 的重量，T 是张力，N 下标 BA 是 B 在 A 上施加的法向力，f 下标 BA 是 B 在 A 上施加的摩擦力。图 b 以相同的方式显示了斜坡上的物体。自由体图有 f 下标 B 和 f 下标 AB 指向右和向上，与斜率平行，N 下标 B 指向左和向上垂直于斜率，w 下标 B 垂直向下指向，N 下标 AB 指向下和向右，垂直于斜率。 W 下标 B 是方块 B 的重量，N 下标 AB 是 A 在 B 上施加的法向力，N 下标 B 是倾斜平面在 B 上施加的法向力 f 下标 AB 施加的摩擦力 f 下标 B 是倾斜平面在 B 上施加的摩擦力 — 图\(\PageIndex{2}\)：(a) 隔离物体 A 的自由体图 A. (b) 隔离物体 B 的自由体图 B 比较两幅图，我们可以看出，摩擦力在两张图中起作用的方向相反。由于物体 A 承受的力往往会将其向右拉，因此摩擦力必须向左起作用。由于物体 B 的重量中有一部分会将其向左拉动，向下倾斜，因此摩擦力必须抵抗它并在坡道上起作用。摩擦力总是与预期的运动方向相反。

现在，我们将作用于身体的任何力量都包括在内。在这里，不存在施加的力。物体的重量充当垂直向下指向的力，绳索的存在表示张力指向远离物体。物体 A 只有一个接口，因此会受到远离接口的法向力。该力的来源是物体 B，相应地标记了该法向力。由于物体 B 有向下滑动的趋势，因此物体 A 倾向于相对于界面向上滑动，因此 f _BA 的摩擦力平行于倾斜平面向下滑动。

正如问题解决策略的第 4 步所述，然后我们使用相同的方法构造图 5.32 (b) 中的自由体图。由于存在两个接触表面，物体 B 会经历两个法向力和两个摩擦力。与倾斜平面的界面施加了 N _{B 和 f B} 的外力，与物体 _B 的界面施加法向力 N _AB 和摩擦力 f _AB；N _AB 指向远离物体 B，f _AB 与物体 B 的趋势相反物体 B 相对于物体 A 的相对运动

意义

这个问题每个部分所考虑的物体都用灰色圈出。当你第一次学习如何绘制自由体图时，你会发现在决定什么力作用在该特定物体上之前，先绕物体圈出来会很有帮助。这会集中你的注意力，防止你考虑不作用于身体的力量

示例\(\PageIndex{2}\): Two Blocks in Contact

对两个接触的方块施加力，如图所示。

策略

为每个方块绘制自由体图。一定要在两个方块接触的界面上考虑牛顿的第三定律。

显示了两个相互接触的方块。左边的比较小，标有 m1。右边的更大，标为 m2。向右指向 m1 的箭头标记为 F。

解决方案

意义

\(\vec{A}_{21}\)是方块 2 对方块 1 的作用力。 \(\vec{A}_{12}\)是方块 1 对方块 2 的反作用力。我们在《牛顿定律的应用》中使用这些自由体图。

示例\(\PageIndex{3}\): Block on the Table (Coupled Blocks)

桌子上有一块方块，如图所示。一根轻绳附在上面，穿过滑轮。绳子的另一端连接到第二个方块上。据说这两个方块是耦合的。方块 m ₂ 由于其重量而施加力，这会导致系统（两个方块和一根绳子）加速。

策略

我们假设字符串没有质量，因此我们不必将其视为一个单独的对象。为每个方块绘制自由体图。

该图显示了放置在桌子上的方块 m1。附着在上面的一根绳子从滑轮上向下延伸到桌子的右侧。一个方块 m2 被悬挂在上面。箭头 a1 指向右，箭头 a2 指向下方。

解决方案

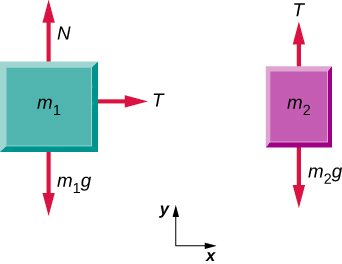
图 a 显示了区块 m1。标有 N 的箭头指向上方，箭头 m1g 指向下方，箭头 T 指向右。图 b 显示了区块 m2。箭头 T 指向上方，箭头 m2g 指向下方。

意义

每个方块都会加速（注意\(\vec{a}_{1}\)和所示的标签\(\vec{a}_{2}\)）；但是，假设字符串保持拉紧，它们会以相同的速度加速。因此，我们有\(\vec{a}_{1}\) | | =\(\vec{a}_{2}\) |。如果我们要继续解决这个问题，我们可以简单地称之为加速\(\vec{a}\)。另外，我们使用两个自由体图，因为我们通常会找到张力 T，这可能需要我们在此类问题中使用两个方程组。 m ₁ 和 m ₂ 的张力相同。

练习\(\PageIndex{1}\)

针对所示情况绘制自由体图。
重绘它以显示组件；使用平行于两个坡道的 x 轴。

两辆手推车用绳子绑在一起，绳子越过山顶上的滑轮。每辆手推车都停在滑轮两侧的山坡上。左边的购物车标有 m1，右边的购物车标记为 m2。

模拟

查看此模拟，定性地预测外力将如何影响物体运动的速度和方向。借助自由体图解释效果。使用自由体图绘制位置、速度、加速度和力图，反之亦然。解释这些图表是如何相互关联的。给定一个场景或一个图表，绘制所有四个图表。