Skip to main content
Global

5.E：牛顿运动定律（练习）

  1. Last updated
  2. Save as PDF
  • Page ID
    205016

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    概念性问题

    5.1 部队

    1. 力具有哪些特性使我们能够将它们归类为向量？

    5.2 牛顿第一定律

    1. 将附着在地球上的框架当作惯性框架，以下哪些物体不能附带惯性框架，哪些是惯性参考框架？
      1. 一辆以恒定速度行驶的汽车
      2. 一辆正在加速的汽车
      3. 自由落体中的电梯
      4. 绕地球运行的太空舱
      5. 电梯均匀下降
    2. 一名妇女正在运送一盒开着的纸杯蛋糕去参加学校聚会。 她面前的汽车突然停了下来；她立即踩了刹车。 她系着安全带，没有受到人身伤害（简直太尴尬了），但是纸杯蛋糕飞到了仪表板上，变成了 “smushcakes”。 解释发生了什么。

    5.3 牛顿第二定律

    1. 当我们应用牛顿第二定律时，为什么我们可以忽略诸如将身体凝聚在一起的力量？
    2. 一块石头被直接向上抛出。 在轨迹的顶部，速度暂时为零。 这是否意味着作用于物体的力为零？ 解释你的答案。

    5.4 质量和重量

    1. 重量和质量之间有什么关系？ 哪个是身体固有的、不变的特性？
    2. 一个70公斤的宇航员在远离任何天体的太空中重量是多少？ 她在这个地方的质量是多少？
    3. 以下陈述中哪一项是正确的？
      1. 质量和重量是相同的，用不同的单位表示。
      2. 如果物体没有重量，则必须没有质量。
      3. 如果物体的重量变化，则质量也必须变化。
      4. 质量和惯性是不同的概念。
      5. 重量始终与质量成正比。
    4. 当你站在地球上时，你的脚会用等于你体重的力量向它推动。 为什么地球没有加速离开你？
    5. 你会如何给出矢\(\vec{g}\)量形式的值？

    5.5 牛顿第三定律

    1. 确定以下情况下的作用和反作用力：
      1. 地球吸引月球，
      2. 一个男孩踢足球，
      3. 火箭向上加速，
      4. 一辆汽车向前加速，
      5. 跳高运动员跳了起来，而且
      6. 子弹是用枪射出的。
    2. 假设你手里拿着一杯咖啡。 确定杯子上的所有力以及对每种力的反应。
    3. (a) 为什么普通步枪在射击时会后坐力（向后踢）？ (b) 无后坐力步枪的枪管两端均已打开。 描述当一个人被射击时牛顿的第三定律是如何适用的。 (c) 当它被射击时你能安全地站在后面吗？

    5.6 普通力量

    1. 桌子放在地毯上。 然后在桌子上放一本书。 地板对什么施加正常力？
    2. 粒子正在向右移动。 (a) 它身上的力量能否向左起作用？ 如果是，会发生什么？ (b) 那支力量能向下作用吗？ 如果是，为什么？

    5.7 绘制自由体图

    1. 在完成涉及力问题的解决方案时，在构造自由体图之后我们该怎么做？ 也就是说，我们适用什么？
    2. 如果一本书位于桌子上，则该书的自由体图中应该显示多少力？ 描述他们。
    3. 如果上一个问题中的书处于自由落体状态，那么这本书的自由体图中应该显示多少力量？ 描述他们。

    问题

    5.1 部队

    1. 两根绳子附着在一棵树上，施加的力分别\(\vec{F}_{1}\)为 = 2.0\(\hat{i}\) + 4.0\(\hat{j}\) N 和\(\vec{F}_{2}\) = 3.0\(\hat{i}\) + 6.0\(\hat{j}\) N。 力是共面的（在同一个平面上）。 (a) 这两个力向量的合成（净力）是什么？ (b) 找出这种净力的大小和方向。
    2. 如上所示，电线杆有三根电缆，分别为\(\vec{F}_{1}\) = (300.0\(\hat{i}\) + 500.0\(\hat{j}\))、\(\vec{F}_{2}\) = −200.0 和\(\hat{i}\)\(\vec{F}_{3}\) = −800.0\(\hat{j}\)。 (a) 以组件形式找到电线杆上的净力。 (b) 找出这种净力的大小和方向。

    图中显示了坐标轴，矢量 F1 与正 y 轴成大约 28 度的角度，沿负 x 轴的向量 F2 和沿负 y 轴的向量 F3。

    1. 两个少年正在拉一棵树上的绳子。 绳索之间的角度为 30.0°。 大卫用 400.0 N 的力拉动，斯蒂芬妮用 300.0 N 的力拉动。(a) 找到净力的分量形式。 (b) 找出树上合成（净）力的大小以及它用大卫的绳子产生的角度。

    5.2 牛顿第一定律

    1. \(\vec{F}_{1}\)= 75.0 2 (\(\hat{i}\)−\(\hat{j}\)) N 和\(\vec{F}_{2}\) =\(\frac{150.0}{\sqrt{2}} (\hat{i} − \hat{j})\) N 的两种力作用于物体。 找到平衡前两种力\(\vec{F}_{3}\)所需的第三种力。
    2. 安德里亚（Andrea）和詹妮弗（Jennifer）在沙发\(\vec{F}_{J}\)上滑动沙发时，施加力量\(\vec{F}_{A}\)。 安德里亚的力量位于北方，震级为北纬130.0，詹妮弗的力量位于北偏东 32°，震级为 180.0 N (a) 以分量形式找到净力。 (b) 找出净力的大小和方向。 (c) 如果安德里亚和詹妮弗的室友大卫和斯蒂芬妮不同意此举并想阻止其搬迁，他们\(\vec{F}_{DS}\)应该用什么联合力量推动沙发不动？

    5.3 牛顿第二定律

    1. 安德里亚是一名63.0公斤的短跑运动员，以4.200 m/s 2 的加速度开始比赛。 她身上的净外力是什么？
    2. 如果前一个问题中的短跑运动员以该速度加速 20.00 m，然后在 100.00 米冲刺的剩余时间内保持该速度，那么她参加比赛的时间是多少？
    3. 清洁工推动 4.50 千克的洗衣车时，其上的净外力为 60.0 N。计算他的购物车加速度的大小。
    4. 轨道上的宇航员显然失重。 这意味着需要一种巧妙的方法来测量宇航员的体重，以监测他们的质量增减并调整他们的饮食。 做到这一点的一种方法是向宇航员施加已知的力，然后测量产生的加速度。 假设施加了 50.0 N 的净外力，测得的宇航员的加速度为 0.893 m/s 2。 (a) 计算她的体重。 (b) 通过对宇航员施加力，她运行的飞行器承受相等和相反的力。 利用这些知识找到系统（宇航员和太空飞船）加速度的方程式，该方程将由附近的观察者测量。 (c) 讨论这将如何影响宇航员加速度的测量。 提出一种避免车辆后坐力的方法。
    5. 在图 5.4.3 中，24 千克割草机上的净外力为 51 N。如果反对运动的摩擦力为 24 N，则该人对割草机施加的力 F（以牛顿为单位）？ 假设移除力 F 后，割草机以 1.5 m/s 的速度移动。 割草机在停下来之前会走多远？
    6. 下图所示的火箭雪橇以 196 m/s 2 的速度减速。 产生这种减速需要什么力？ 假设火箭已关闭。 该系统的质量为 2.10 x 10 3 千克。

    图中显示了指向右侧的火箭雪橇。 左侧点的摩擦力。 向上力 N 和向下力 w 的大小相等。

    1. 如果上一个问题中显示的火箭雪橇开始时只有一枚火箭燃烧，那么这种加速的幅度是多少？ 假设系统的质量为 2.10 x 10 3 kg，推力 T 为 2.40 x 10 4 N，反对运动的摩擦力为 650.0 N。(b) 为什么加速度不是所有火箭燃烧时的四分之一？
    2. 如果火箭雪橇在 1.10 秒内从 1000.0 km/h 的速度静止，其减速会是多少？ （这种减速导致一名测试对象停电并暂时失明。）
    3. 假设两个孩子在马车里水平推动，但方向完全相反。 第一个孩子施加的力为 75.0 N，第二个孩子施加 90.0 N 的力，摩擦力为 12.0 N，第三个 child plus 旅行车的质量为 23.0 kg。 (a) 如果要计算孩子在马车上的加速度，利息系统是什么？ （参见自由体图。） (b) 计算加速度。 (c) 如果摩擦力为 15.0 N，加速度会是多少？

    该图显示了免费人体图。 向右强制 Fr 点，强制 N 点向上，强制 Fl 和 f 点向左，强制 w 点向下。

    1. 一辆强劲的摩托车在以 90.0 km/h 的速度行驶时可以产生 3.50 m/s 2 的加速度。在该速度下，包括摩擦和空气阻力在内的阻力总计 400.0 N（空气阻力类似于空气摩擦。 它总是反对物体的运动。） 如果有骑手的摩托车的重量为245 kg，摩托车在地面上向后施加的力是多少？
    2. 重量为 1000.0 kg 的汽车在 10.0 秒内从 0 km/h 加速到 90.0 km/h。(a) 它的加速度是多少？ (b) 汽车上的净力是多少？
    3. 前面问题中的驾驶员在汽车以 90.0 km/h 的速度行驶时刹车，汽车在行驶 40.0 m 后休息。汽车减速期间的净力是多少？
    4. 一名 80.0 公斤的乘客乘坐以 1.00 x 10 2 km/h 的速度行驶的 SUV，正在系安全带。 驾驶员踩刹车，SUV 在 45.0 米处停下来。找出安全带对乘客的力。
    5. 质量为 2.0 kg 的粒子受单力\(\vec{F}_{1}\) = 18\(\hat{i}\) N 的作用力。(a) 粒子的加速度是多少？ (b) 如果粒子从静止状态开始，它在最初的 5.0 秒内会传播多远？
    6. 假设前一个问题的粒子也经历了力\(\vec{F}_{2}\) = −15\(\hat{i}\) N 和\(\vec{F}_{3}\) = 6.0\(\hat{j}\) N 在这种情况下它的加速度是多少？
    7. 找到如下所示的质量体加速度 5.0 kg。

    该图显示了 xy 平面中标有 m 的圆。 三支箭从中产生。 一个指向右边，被标记为 10 i 牛顿。 另一个点在左边，被标记为 -2 i newtons。 第三个指向下方，标记为 — 4 j 牛顿。

    1. 在下图中，该方块滑动的水平表面是无摩擦的。 如果作用于它的两个力的幅度均为 F = 30.0 N，M = 10.0 kg，那么由此产生的方块加速度的大小是多少？

    该图显示了一个标有 M 的盒子放在表面上。 与水平方向形成零下 30 度角度的箭头被标记为 F 并指向方框。 另一个标有 F 的箭头指向右边。

    5.4 质量和重量

    1. 宇航员加上他在月球上的太空服的重量只有 250 N。(a) 合适的宇航员在地球上的重量是多少？ (b) 月球上的质量是多少？ 在地球上？
    2. 假设宇航员从月球起飞的满载舱的质量为 1.00 x 10 4 kg。 其发动机的推力为 3.00 x 10 4 N。(a) 计算模块在从月球垂直起飞时的加速度大小。 (b) 它能从地球升空吗？ 如果不是，为什么不呢？ 如果可以，计算其加速度的大小。
    3. 火箭雪橇以 49.0 m/s 2 的速度加速。 它的乘客体重为75.0千克。 (a) 计算座椅对其身体施加的力的水平分量。 用比率将其与他的体重进行比较。 (b) 计算座椅对其身体施加的总力的方向和大小。
    4. 在火箭雪橇以 201 m/s 2 的速度减速的情况下，重复前面的问题。 在这个问题中，力是由座椅和安全带施加的。
    5. 重量为 2.00 kg 的体通过 25.0 N 的垂直力直接向上推动。 它的加速度是多少？
    6. 一辆重 12,500 N 的汽车从静止状态开始，在 5.00 秒内加速到 83.0 km/h。摩擦力为 1350 N。找到发动机产生的施加力。
    7. 假定质量为10.0 kg的天体位于地球的引力场中，g = 9.80 m/s 2。 如果没有其他外力作用在物体上，身体上的净力是多少？
    8. 消防员的质量为 m；他听到火警并以加速度 a（幅度小于 g）向下滑动杆子。 (a) 写一个方程，给出他必须对极点施加的垂直力。 (b) 如果他的质量为 90.0 kg 并且他以 5.00 m/s 2 的速度加速，那么他施加的力的大小是多少？
    9. 一名棒球接球手正在为电视广告表演特技。 他将抓住从手套上方 60.0 米的高度掉落的棒球（质量 145 g）。 他的手套在 0.0100 秒内阻止球。他的手套对球施加的力量是多少？
    10. 当月球在日落时直接位于头顶时，地球在月球上的力 F EM 基本上与太阳对月球的力 F SM 为 90°，如下所示。 鉴于 F EM = 1.98 x 10 20 N 和 F SM = 4.36 x 10 20 N，月球上的所有其他力都可以忽略不计，月球的质量为 7.35 x 10 22 kg，确定月球加速度的大小。

    该图显示了一个标有月亮的圆圈。 它的箭头指向上方，标记为 F 下标 EM。 另一个指向右侧的箭头标记为 F 下标 SM。

    5.5 牛顿第三定律

    1. (a) 如果炮弹以 2.40 x 10 4 m/s 2 的速度加速，则对从战舰发射的 110.0 千克炮弹施加多少净外力？ (b) 炮弹对舰艇施加的力量有多大，为什么？
    2. 一名勇敢但不足的橄榄球运动员正被对方球员向后推，该球员正在向他施加800.0 N的力量。 输掉的玩家加上装备的质量为90.0 kg，他以 1.20 m/s 2 的速度向后加速。 (a) 输掉玩家的脚和草地之间的摩擦力是多少？ (b) 如果获胜玩家的质量加上装备为 110.0 kg，他会在地面上施加什么力量来向前移动？
    3. 一本历史书躺在桌子上的一本物理书的顶部，如下所示；还显示了自由体图。 历史和物理书分别重 14 N 和 18 N。 用双下标符号标识每本书上的每种力（例如，历史书籍压在物理书上的接触力可以描述为\(\vec{F}_{HP}\)），然后确定每种力的值，解释所使用的过程。

    图中显示了两张免费身体图。 第一个有 F 下标 ph 指向上方，F 下标 eh 指向下方。 第二个是 F 下标 dp 指向上方，F 下标 hp 和 F 下标 ep 指向下方。

    1. 卡车与汽车碰撞，在碰撞期间，每辆车上的净力本质上是另一辆车施加的力。 假设汽车的质量为 550 千克，卡车的质量为 2200 千克，卡车的加速度大小为 10 m/s 2。 找出汽车加速度的大小。

    5.6 普通力量

    1. 腿悬挂在牵引系统中，如下所示。 (a) 图中的哪一部分用于计算施加在脚上的力？ (b) 绳索的张力是多少？ \(\vec{T}\)这是张力，\(\vec{w}_{leg}\)是腿的重量，\(\vec{w}\)是提供张力的负荷的重量。

    该图显示左边有一条腿。 它固定在脚踝处的绳子上，悬挂在顶部的滑轮上。 绳索延伸到第一个滑轮右侧的第二个滑轮，第三个滑轮延伸到第二个滑轮的底部，第四个滑轮延伸到第三个滑轮的左下角，第五个滑轮延伸到第四个滑轮的右下角。 绳索末端附着一个重量为 w = mg 的物体。 标有 w 下标腿的箭头指向脚踝向下方，标有 T 的箭头从脚踝指向上方。 标有 T 的箭头，从第四个滑轮到第三个滑轮，与水平方向形成一个角度 theta。 另一个标有 T 的箭头，从第四个滑轮到第五个滑轮与水平方向形成一个减去 theta 的角度。

    1. 假设上图中的胫骨是骨折的牵引装置中的股骨，有滑轮和绳索可用。 我们怎么能用同样的重量增加股骨上的力？
    2. 一支由九名成员组成的团队在一座高层建筑上拖着一根附在冰冷表面上的大巨石上的绳子。 这块巨石的质量为 200 kg，被拉动的力为 2350 N。(a) 加速度的大小是多少？ (b) 产生恒定速度需要什么力？
    3. 蹦床必须对身高 45.0 公斤的体操运动员詹妮弗施加什么力量才能以 7.50 m/s 2 的速度直线加速她？ 答案与体操运动员的速度无关，她可以向上或向下移动，也可以立即保持静止。
    4. (a) 如果质量为 2.00 x 10 −5 kg 的蜘蛛一动不动地悬挂在一根垂直的蜘蛛网上，则计算其张力。 (b) 计算如果同一只蜘蛛一动不动地坐在蜘蛛网的中间，就像图 5.26 中的走钢丝一样，则计算其中的张力。 股线以低于水平线12°的角度下垂。 将其与垂直股线中的张力进行比较（找出它们的比例）。
    5. 假设60.0公斤的体操运动员凯文爬上一根绳子。 (a) 如果他以恒定速度攀爬，绳索的张力是多少？ (b) 如果他以 1.50 m/s 2 的速度向上加速，绳索的张力是多少？
    6. 表明，正如文本中所解释的那样，\(\perp\)施加在柔性介质中心并垂直于其长度的力 F（如图 5.26 中的钢丝上）会产生数量级的张力\(T = \frac{F_{\perp}}{2 \sin \theta}\)。
    7. 以图 5.28 为例。 驾驶员试图通过施加610.0 N的垂直力使汽车脱离泥巴，她在绳索中间推动的距离为1.00 m，而她站在左侧距离汽车6.00米，距离右边的树6.00米。 绳子里的张力 T 是多少，你如何找到答案？
    8. 一只鸟的重量为 26 g，栖息在延伸的电话线中间。 (a) 表明可以使用方程式计算直线中的张力\(T = \frac{mg}{2 \sin \theta}\)。 在 (b)\(\theta\) = 5° 且 (c)\(\theta\) = 0.5° 时确定张力。 假设这条线的每一半都是直线。

    该图显示一只鸟坐在两端固定的电线上。 电线会随着其重量而下垂，形成一个角度 theta，两侧的水平线都是 theta。

    1. 一根 30 米长的绳子的一端绑在树上；另一端绑在一辆被困在泥里的汽车上。 驾驶者在绳索的中点侧向拉动，将其移动 2 m 的距离。如果他在这种条件下施加了 80 N 的力，请确定施加在汽车上的力。
    2. 考虑下图中宝宝的体重情况。 (a) 如果观察到刻度读数为 55 N，则婴儿和篮子的质量是多少？ (b) 将宝宝连接到体重秤的绳索中的张力 T 1 是多少？ (c) 如果天平的质量为 0.500 kg，则将体重秤连接到天花板的绳索中的张力 T 2 是多少？ (d) 概述情况，指出用于求解每个部分的感兴趣系统。 绳索的质量可以忽略不计。

    该图显示了一个装在装有弹簧秤的篮子里的婴儿，弹簧秤反过来又由刚性支撑物固定。 箭头 T2 指向支撑向下方。 另一个箭头 T2 从刻度顶部向上指向。 箭头 T1 从刻度底部向下指向。 另一支箭头 T1 从篮子向上指向。 箭头 w 指向篮筐。 刻度上有从 0 到 300 牛顿的标记。

    1. 必须对倾斜度为 30° 的无摩擦平面上的 100.0 千克的箱子施加什么力才能使飞机向上加速 2.0 m/s 2？

    该图显示了一个斜率为 30 度的物体。 指向上方且平行于斜率的箭头标为 F。

    1. 一个 2.0 千克的方块位于非常平滑的坡道上，与水平方向成了 30° 的角度。 (a) 方块向下坡道的加速度和方块上坡道的力量是多少？ (b) 沿着坡道向上平行施加什么力可以使方块以恒定速度移动？

    5.7 绘制自由体图

    1. 一个质量球 m 悬挂在静止状态，被一根绳子悬挂。 (a) 绘制所有力的草图。 (b) 绘制球的自由体图。
    2. 汽车沿着水平道路行驶。 绘制自由车身图；一定要包括与汽车向前运动相反的道路摩擦力。
    3. 跑步者向赛道推动，如图所示。 (a) 提供自由体图，显示跑步者身上的所有力。 （提示：将所有力量放在他的身体中心，包括他的体重。） (b) 给出一张显示 xy 组件表单的修订图。

    显示了一张男子向右奔跑的照片。 标有 F 的箭头从地板向上和向右指向他的脚。

    1. 如图所示，交通信号灯悬挂在电缆上。 在这种情况下，在坐标平面上绘制自由体图。

    图中显示了一个红绿灯，由另外三根电缆 T1、T2 和 T3 悬挂在水平电缆上。 T1 向下向右悬挂，与水平电缆成为 41 度的角度。 T2 向下和向左悬挂，与水平电缆成为 63 度的角度。 它们在某个点相交然后 T3 从这里垂直向下悬挂。 灯连接到 T3。 从光源向下指向的矢量被标记为 w 等于 200 牛顿。

    其他问题

    1. 两支小力量，\(\vec{F}_{1}\)= −2.40\(\hat{i}\) − 6.10t\(\hat{j}\) N 和\(\vec{F}_{2}\) = 8.50\(\hat{i}\) − 9.70\(\hat{j}\) N，由一对太空拖拉机对流氓小行星施加。 (a) 找到净力。 (b) 净力的大小和方向是多少？ (c) 如果小行星的质量为125 kg，它会经历多大的加速度（矢量形式）？ (d) 加速度的大小和方向是多少？
    2. 25 和 45 N 的两种力作用于物体。 它们的方向相差70°。 由此产生的加速度的幅度为 10.0 m/s 2。 身体的质量是多少？
    3. 1600 N 的力与坡道平行作用，将一架 300 千克的钢琴推入行驶中的货车。 坡道倾斜度为 20°。 (a) 钢琴在坡道上的加速度是多少？ (b) 如果坡道长 4.0 m 且钢琴从静止状态开始，钢琴到达顶部时的速度是多少？
    4. 绘制一张自由体图，描绘一名潜水员已进入水中，向下移动，并由于平衡体重（即潜水员处于悬浮状态）而受到向上力的作用。
    5. 对于刚跳下跳水板的游泳运动员来说，假设空气阻力可以忽略不计。 游泳运动员的体重为80.0 kg，在距离水面 10.0 米处跳下滑板。 进入水中三秒钟后，她的向下动作停止了。 水对她施加的平均向上力是多少？
    6. (a) 找一个方程来确定停止质量为 m 的汽车所需的净力的大小，假设汽车的初始速度为 v 0，停止距离为 x。(b) 如果汽车的质量为 1050 kg，初始速度为 40.0 km/h，则找出净力的大小距离是 25.0 米。
    7. 帆船的质量为 1.50 x 10 3 千克，以 2.00 x 10 3 N 的力向东起作用，而风在帆后面以 3.00 x 10 3 N 的力向东以北 45° 的方向起作用。 找出所得加速度的大小和方向。
    8. 找到如下所示的质量体加速度 10.0 kg。

    三个箭头从标有 m. F1 的圆向外辐射，等于 10 N，垂直向下指向。 F2 等于 20 N，指向上和向右，与 y 轴正方向成负 37 度的角度。 F3，等于 10 N，向上和向左指向，与 y 轴正方向成为 37 度的角度。

    1. 质量为 2.0 kg 的物体正沿 x 轴移动，速度为 3.0 m/s，如下所示。 (a) 身体的加速度是多少？ (b) 10.0 秒后人体的速度是多少？ (c) 10.0 秒后它的位移是多少？

    三个箭头从标有 m. F1 的圆向外辐射，等于 50 N，指向上和向右，与 x 轴成为 37 度的角度。 F2，等于 30 N，指向左和向下，与 y 轴为负 30 度。 F3，等于 80 N，向左点。

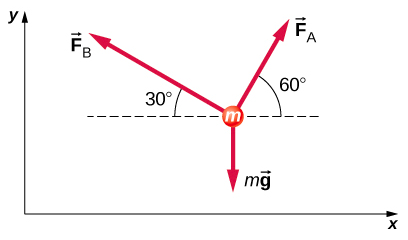
    1. 力\(\vec{F}_{B}\)的大小是力的两倍\(\vec{F}_{A}\)。 在此图中找到粒子加速的方向。

    两个箭头从标有 m 的圆向外辐射。F 下标 A 指向右边。 F 下标 B 指向下和向左，与水平方向成45度的角度。

    1. 下图显示的是受力\(\vec{F}_{A}\)、\(\vec{F}_{B}\)和 m 影响下质量为 1.0 kg 的物体\(\vec{g}\)。 如果身体以 20 m/s 2 的速度向左加速，那么 and\(\vec{F}_{A}\) 是什么\(\vec{F}_{B}\)？

    三个箭头从标有 m. F 下标 A 的点向外辐射，与负 x 轴成为 60 度的角度。 F 下标 B 指向左和向上，与负 x 轴形成零下 30 度的角度。 矢量 mg 指向垂直向下。

    1. 力作用于质量为 m 的汽车，因此汽车的速度 v 随位置 x 的增加，为 v = kx 2，其中 k 是恒定的，所有量都以 SI 为单位。 找出作用于汽车的力作为位置的函数。
    2. 对一个 1.0 千克的箱子施加平行于斜度的 7.0-N 力。 坡道倾斜20°，无摩擦。 (a) 箱子的加速度是多少？ (b) 如果所有其他条件都相同，但坡道的摩擦力为 1.9 N，则加速度是多少？
    3. 两个盒子，A 和 B，处于静止状态。 方块 A 位于水平地面上，而方块 B 位于\(\theta\)与水平成一定角度倾斜的倾斜平面上。 (a) 写出作用于每个方块的法向力的表达式。 (b) 比较这两种力；也就是说，判断哪一个力更大，或者它们的幅度是否相等。 (c) 如果倾角为 10°，哪个力更大？
    4. 250.0 g 的质量悬挂在垂直悬挂的弹簧上。 弹簧延伸6.00厘米。 如果悬浮质量为 530.0 g，弹簧会伸展多少？
    5. 如下所示，两个相同的弹簧，每个弹簧的弹簧常数为 20 N/m，支撑的重量为 15.0-N。 (a) 弹簧A的张力是多少？ (b) 弹簧 A 距离静止位置的伸展量是多少？

    该图显示了两个相同的弹簧并排悬挂。 它们的下端聚集在一起，可以支撑重量。 每个弹簧与垂直方向成30度的角度。

    1. 下图是一个重达 30.0 kg 的方块，位于向水平方向倾斜 60° 的无摩擦坡道上。 方块由拉伸 5.0 厘米的弹簧固定。 弹簧的力常数是多少？

    图中显示了一个向下和向左倾斜的曲面，与水平方向成了 60 度的角度。 一个重达 30 kg 的物体悬挂在弹簧上，停在斜坡上。

    1. 在建造房屋时，木匠使用大盒子里的钉子。 白天将盒子悬挂在弹簧上两次，以测量指甲的使用情况。 一天开始时，春天延伸50厘米。 归根结底，春天延伸30厘米。 使用了多少或百分比的指甲？
    2. 对方块施加力使其向上移动 30° 的斜度。 斜坡无摩擦。 如果 F = 65.0 N 且 M = 5.00 kg，则方块加速度的大小是多少？

    图中显示了一个向下和向右倾斜的曲面，与水平方向成了 30 度的角度。 上面有一个标有 M 的盒子。 标有 F 的箭头水平向左指向方框。 箭头和斜率形成的角度为 30 度。

    1. 对一个 5.0 kg 的物体施加两个力，它在 y 方向上以 2.0 m/s 2 的速度加速。 如果其中一个力作用于正 x 方向，大小为 12.0 N，则求出另一力的大小。
    2. 如下所示右侧方块的质量大于左边的方块（m 2 > m 1）。 为每个方块绘制自由体图。

    滑轮安装在天花板上。 一根绳子越过了它。 绳索的左端附着一个质量块 m1，另一个标有 m2 的方块附着在绳索的右端。 M2 的挂起速度低于 m1。

    挑战问题

    1. 如果两艘拖船驶向一艘残障船只，如俯视图所示，则残疾船只将沿着施加力量的结果所示的方向拉动。 (a) 绘制船只的自由体图。 假设没有摩擦力或阻力影响船只。 (b) 你是否在自由体图中包含了俯视图中的所有力？ 为什么或者为什么不呢？

    该图显示了两艘拖船将一艘残疾船只向左拉动的俯视图。 Arrow F1 位于连接船只和顶部拖船的线上。 箭头 F2 位于连接船只和底部拖船的线上。 F1 比 F2 长。 箭头 F 下标 R 表示组合力。 它介于 F1 和 F2 之间，指向左边，稍微向上。

    1. 一个 10.0 kg 的物体最初以 15.0 m/s 的速度向东移动。然后力作用于它 2.00 秒，之后它向西北移动，也以 15.0 m/s 的速度移动。在 2.00 秒间隔内作用于该物体的平均力的大小和方向是多少？
    2. 1983年6月25日，东德的推杆手乌多·拜尔投出了7.26公斤的射门22.22米，这是当时的世界纪录。 (a) 如果射击是在2.20 m的高度释放的，投射角度为45.0°，则其初始速度是多少？ (b) 如果在 Beyer 手中射门在 1.20 米的距离内均匀加速，那么它的净力量是多少？
    3. 质量体 m 沿水平方向移动，因此在时间 t 时，其位置由 x (t) = 在 4 + bt 3 + ct 处给出，其中 a、b 和 c 是常数。 (a) 身体的加速度是多少？ (b) 作用于身体的随时间变化的力是什么？
    4. 质体 m 在正 x 方向上的初始速度 v 0。 它在时间 t 内受恒定力 F 的作用直到速度变为零；该力继续作用于身体，直到其速度在相同的时间内变为 −v 0。 根据指示的变量写一个表达式，表示身体行进的总距离。
    5. 在 t = 6.0 秒和 t = 8.0 秒时，3.0 千克物体的速度分别为 (3.0\(\hat{i}\) − 6.0\(\hat{j}\) + 4.0\(\hat{k}\)) m/s 和 (−2.0\(\hat{i}\) + 4.0\(\hat{k}\)) m/s。 如果物体以恒定加速度移动，则作用在其上的力是多少？
    6. 一名120公斤的宇航员乘坐火箭雪橇，该雪橇沿着倾斜的飞机滑动。 雪橇的水平加速度分量为 5.0 m/s 2，向下分量为 3.8 m/s 2。 计算雪橇对骑手施加的力的大小。 （提示：请记住，必须考虑引力加速度。）
    7. 两个力作用于一个 5.0 kg 的物体上，该物体以 2.0 m/s 2 的加速度在正 y 方向移动。 如果其中一个力在正 x 方向上作用并且其大小为 12 N，则另一个力的大小是多少？
    8. 假设你正在运动场上方的直升机上观看足球比赛。 两名足球运动员同时在平坦的场地上踢一个固定的足球；足球的重量为0.420 kg。 第一个玩家在西部以北 9.0° 处以 162 N 的力量踢球。 同时，第二名玩家在南方以东 15° 处以 215 N 的力量踢球。 在形态中找到球的\(\hat{i}\)加\(\hat{j}\)速度。
    9. 弹簧常数为 535 N/m 的弹簧上悬挂着 10.0 千克的质量。找出弹簧末端的位置远离其静止位置。 （使用 g = 9.80 m/s 2。）
    10. 一对 0.0502 千克的模糊骰子用一根短绳子固定在汽车的后视镜上。 赛车以恒定速度加速，由于赛车的加速，骰子与垂直方向成3.20°的角度悬挂。 汽车的加速度大小是多少？
    11. 在马戏团里，一头驴用2.48\(\hat{i}\) + 4.33 N施加的力量拉着一个小丑的雪\(\hat{j}\)橇。 一匹马拉着同一个雪橇，帮助那头不幸的驴，力为 6.56\(\hat{i}\) + 5.33\(\hat{j}\) N。雪橇的质量为 575 千克。 使用\(\hat{i}\) and f\(\hat{j}\) orm 作为每个问题的答案，求出 (a) 两只动物共同作用时雪橇上的净力，(b) 雪橇的加速度，以及 (c) 6.50 秒之后的速度。
    12. 悬挂在天花板上的婴儿床上，宝宝触手可及，是一根塑料形状的绳子，如图所示。 绳子是拉紧的（没有松弛），如直线段所示。 如图所示，每个塑料形状的质量 m 相同，并且它们的间距相等 d。 标记的角度\(\theta\)描述了绳子末端和两端的天花板所形成的角度。 字符串的中心长度是水平的。 剩下的两条线段各与水平线形成一个角度，标有标签\(\phi\)。 假设 T 1 是琴弦最左侧部分的张力，T 2 是与其相邻部分的张力，T 3 是水平段中的张力。 (a) 根据变量 m、g 和，找出字符串每个部分的张力方程\(\theta\)。 (b) 根据角度\(\phi\)找出角度\(\theta\)。 (c) 如果\(\theta\) = 5.10°，其值是多少\(\phi\)？ (d) 找出以 d 和为单位的端点之间的距离 x\(\theta\)。

    该图显示了四个形状悬挂在两端天花板上的绳子上。 这些形状将字符串分成五个相等的段，每个段的长度为 d。中间段是水平的。 字符串两端之间的距离为 x。天花板和最靠近天花板的段之间的角度均标记为 theta。 由来自天花板的第一段及其相邻段形成的角度均标记为 phi。

    1. 步枪射出的子弹质量为 10.0 g，以 350 m/s 的速度向右移动。它击中目标，一大袋沙子，穿透距离为 34.0 厘米。 找出减速和阻挡子弹的减速力的大小和方向。
    2. 物体受到三种同时力的作用：\(\vec{F}_{1}\)=( −3.00\(\hat{i}\) + 2.00\(\hat{j}\)) N、\(\vec{F}_{2}\) = (6.00\(\hat{i}\) − 4.00\(\hat{i}\)) N 和\(\vec{F}_{3}\) = (2.00\(\hat{i}\) + 5.00\(\hat{i}\)) N。物体经历 4.23 m/s 2 的加速度。 (a) 以 m 为单位找到加速度矢量。(b) 求出物体的质量。 (c) 如果物体从静止状态开始，则在 5.00 秒后找到其速度。(d) 在 5.00 秒后找到物体速度的分量。
    3. 在粒子加速器中，质子的质量为1.67 x 10 −27 kg，初始速度为 2.00 x 10 5 m/s。它沿直线移动，其速度在 10.0 cm 的距离内增加到 9.00 x 10 5 m/s。 假设加速度是恒定的。 找出施加在质子上的力的大小。
    4. 一架无人机正被引导穿过无摩擦的冰封湖泊。 无人机的质量为 1.50 kg，速度为 3.00\(\hat{i}\) m/s。10.0 秒后，速度为 9.00\(\hat{i}\) + 4.00\(\hat{j}\) m/s。如果水平方向的恒定力导致了这种运动变化，请找出 (a) 力的分量和 (b) 力的大小。

    贡献者和归因

    Template:ContribOpenStaxUni