4.2: 位移和速度向量

Last updated
Save as PDF

Page ID: 204874

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

计算多维位移问题中的位置向量。
求解二维或三维位移。
将位置向量作为时间函数计算速度矢量。
计算多个维度的平均速度。

二维或三维的位移和速度是一维定义的直接扩展。但是，现在它们是向量量，因此使用它们进行计算必须遵循向量代数的规则，而不是标量代数的规则。

位移向量

要描述二维和三维运动，我们必须首先建立坐标系和轴惯例。我们通常使用坐标$x$$y$、和$z$来定位三维点$P(x, y, z)$上的粒子。如果粒子在移动，则变量$x$$y$、和$z$是时间的函数 ($t$)：

\[x = x(t) \quad y = y(t) \quad z = z(t) \ldotp \label{4.1}\]

从坐标系原点到点 P 的位置向量为$\vec{r}(t)$。在坐标系和矢量分量中引入的单位向量表示法中，$\vec{r}$(t) 是

\[\vec{r} (t) = x(t)\; \hat{i} + y(t)\; \hat{j} + z(t)\; \hat{k} \ldotp \label{4.2}\]

该图$\PageIndex{1}$显示了坐标系和指向的向量$P$，粒子在特定时间可能位于哪里$t$。注意 x、y 和 z 轴的方向。这种方向被称为右手坐标系，在整章中都使用它。

显示 x y z 坐标系，正的 x 位于页面外，正 y 向右，正 z 向上。显示了一个点 P，其坐标为 x 为 t，y 为 t，z 为 t。 P 的所有坐标均为正坐标。 t 从原点到 P 的向量 r 也显示为紫色箭头。 t 的 x 坐标、t 的 y 坐标和 t 的 z 坐标显示为虚线。 t 的 X 是 x y 平面中的一条线段，平行于 x 轴，y of t 是 x y 平面中平行于 y 轴的分段，t 的 z 是平行于 z 轴的分段。 — 图$\PageIndex{1}$：位置上有一个粒子的三维坐标系$P(x(t), y(t), z(t))$。

通过我们对粒子在三维空间中的位置的定义，我们可以计算出三维位移。图中$\PageIndex{3}$显示了时间 t _{1 处位于 P ₁} 的粒子，其位置向量$\vec{r}$ (t ₁)。在稍后的时间 t ₂ 中，粒子位于具有位置向量$\vec{r}$ (t ₂) 的 P ₂ 处。位移向量$\Delta \vec{r}$是通过减去以下值得$\vec{r}(t_1)$出的$\vec{r}(t_2)$：

\[\Delta \vec{r} = \vec{r} (t_{2}) - \vec{r} (t_{1}) \ldotp \label{4.3}\]

向量加法将在向量中讨论。请注意，这与我们在一维上所做的操作相同，但现在向量位于三维空间中。

显示 x y z 坐标系，正的 x 位于页面外，正 y 向右，正 z 向上。显示了两个点，P 1 和 P 2。从原点到 P 1 的 t 1 的向量 r 和从原点到 P 2 的 t 2 的向量 r 显示为紫色箭头。向量 delta r 显示为紫色箭头，其尾巴位于 P 1，头部位于 P 2。 — 图$\PageIndex{2}$：位移$\Delta \vec{r} = \vec{r}(t_2) − \vec{r}(t_1)$是从到$P_1$的向量$P_2$。

以下示例说明了多维位移的概念。

示例 4.1：极地轨道卫星

一颗卫星在环绕地球的环极轨道上，高度为 400 km，也就是说，它直接在北极和南极通过头顶。从位移向量直接位于北极上方到纬度 −45° 时，位移向量的大小和方向是多少？

策略

我们绘制问题图片，以图形化方式显示解决方案。这将有助于我们对流离失所问题的理解。然后，我们使用单位向量来求解位移。

解决方案

该图$\PageIndex{3}$显示了地球表面和代表卫星轨道的圆圈。尽管卫星在三维空间中移动，但它们沿着椭圆的轨迹移动，椭圆轨迹可以用二维绘制出来。位置向量是从地球中心绘制的，我们将其视为坐标系的原点，y 轴为北，x 轴为东。它们之间的向量是卫星的位移。我们将地球的半径定为 6370 km，因此每个位置向量的长度为 6770 km。

显示了以地球为中心的 x y 坐标系。正 x 向东，正 y 向北。图中显示了一个大于地球并与地球同心的蓝色圆圈。 t 1 的向量 r 是一个橙色箭头，从原点到蓝色圆圈与 y 轴交叉的位置（从 x 轴正向逆时针方向 90 度）。 t 2 的向量 r 是从原点到蓝色圆圈上零下 45 度的位置的橙色箭头。 Delta r vector 显示为指向下和向右的紫色箭头，从 t 1 的向量 r 的头部开始，到 t 2 向量 r 的头部结束。 — 图$\PageIndex{3}$：两个位置向量是从地球中心（坐标系的原点）绘制的，y 轴为北，x 轴为东。它们之间的向量是卫星的位移。

在单位向量表示法中，位置向量是

\[ \begin{align*} \vec{r}(t_{1}) &= 6770 \ldotp \; km\; \hat{j} \\[4pt] \vec{r}(t_{2}) &= 6770 \ldotp \; km (\cos (-45°))\; \hat{i} + 6770 \ldotp \; km (\sin(−45°))\; \hat{j} \ldotp \end{align*}\]

计算正弦和余弦值，我们有

\[ \begin{align*} \vec{r}(t_{1}) &= 6770 \ldotp \hat{j} \\[4pt] \vec{r}(t_{2}) &= 4787\; \hat{i} − 4787\; \hat{j} \ldotp \end{align*}\]

现在我们可以找到$\Delta \vec{r}$卫星的位移：

\[\Delta \vec{r} = \vec{r} (t_{2}) - \vec{r} (t_{1}) = 4787\; \hat{i} - 11,557\; \hat{j} \ldotp \nonumber\]

位移的幅度为

\[|\Delta \vec{r}| = \sqrt{(4787)^{2} + (-11,557)^{2}} = 12,509\; km. \nonumber\]

位移与 x 轴的角度为

\[\theta = \tan^{-1} \left(\dfrac{-11,557}{4787}\right) = -67.5^{o} \nonumber.\]

意义

绘制位移图为问题的单位向量解提供了信息和意义。在绘制位移时，我们需要包括其分量及其大小以及它与所选轴（在本例中为 x 轴）所形成的角度（图$\PageIndex{4}$）。

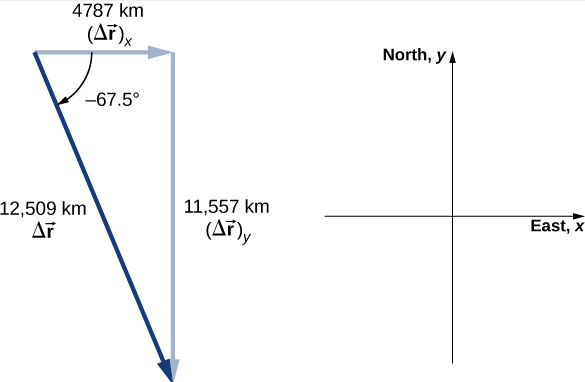
显示了 x y 坐标系。正 x 向东，正 y 向北。矢量 delta r sub x 指向东方，震级 4787 千米。矢量 delta r sub y 指向南方，幅度为 11,557 千米。向量 delta r 指向东南，从 delta r sub x 的尾部开始，在 delta r sub y 的顶部结束，幅度为 12,509 千米。 — 图$\PageIndex{4}$：包含分量、角度和幅度的位移矢量。

请注意，在本例中，卫星沿着其圆形轨道走了一条曲线路以从其初始位置到达最终位置。它也可以向东行驶4787公里，然后向南行驶11,557公里才能到达同一地点。这两条路径都比位移向量的长度长。实际上，位移向量提供了一维、二维或三维两点之间的最短路径。

如前一章所述，物理学中的许多应用可能会产生一系列位移。总位移是单个位移的总和，只是这一次，我们需要小心，因为我们在添加向量。我们用布朗运动的例子来说明这个概念。

示例 4.2：布朗运动

布朗运动是悬浮在流体中的粒子的混乱随机运动，由与流体分子碰撞而产生。这个动作是三维的。正在进行布朗运动的粒子按数值顺序排列的位移可能如下所示，单位为微米（图$\PageIndex{5}$）：

\[\Delta \vec{r}_{1} = 2.0\; \hat{i} + \hat{j} + 3.0 \hat{k}\]

\[\Delta \vec{r}_{2} = - \hat{i} + 3.0\; \hat{k}\]

\[\Delta \vec{r}_{3} = 4.0\; \hat{i} -2.0\; \hat{j} + \hat{k}\]

\[\Delta \vec{r}_{4} = -3.0\; \hat{i} + \hat{j} + 3.0\; \hat{k} \ldotp\]

粒子相对于原点的总位移量是多少？

显示了一个 x y z 坐标系，其距离以微米为单位测量，范围介于 -10 到 +10 微米之间。位移 delta r sub 1 等于 2 I hat plus j hat plus 2 k hat，delta r sub 2 等于 -1 I hat plus 3 k hat，delta r sub 3 等于 -3 I hat plus j hat plus 2 k hat 显示为蓝线段。从原点开始的向量 r 1。随后的每次位移从前一个位移结束处开始。向量 delta r total 显示为一条红线，从矢量 delta r 4 的原点开始，结束于矢量 delta r 4 的末尾。 Delta r total 等于 2 I hat 加 0 y hat 加上 9 k 帽子。 — 图$\PageIndex{5}$：遭受布朗运动随机位移的粒子的轨迹。总排量以红色显示。

解决方案

我们得出位移的总和并将它们相加为向量：

\[\begin{split} \Delta \vec{r}_{Total} & = \sum \Delta \vec{r}_{i} = \Delta \vec{r}_{1} + \Delta \vec{r}_{2} + \Delta \vec{r}_{3} + \Delta \vec{r}_{4} \\ & = (2.0 - 1.0 + 4.0 - 3.0)\; \hat{i} + (1.0 + 0 - 2.0 + 1.0)\; \hat{j} + (3.0 +3.0 + 1.0 + 2.0)\; \hat{k} \\ & = 2.0\; \hat{i} + 0\; \hat{j} + 9.0\; \hat{k}\; \mu m \ldotp \end{split}\]

为了完成解，我们将位移表示为量级和方向，

\[| \Delta \vec{r}_{Total}| = \sqrt{2.0^{2} + 0^{2} + 9.0^{2}} = 9.2 \mu m, \quad \theta = \tan^{-1} \left(\dfrac{9}{2}\right) = 77^{o},\]

相对于xz平面中的x轴。

意义

从图中我们可以看出，总位移的幅度小于单个位移的幅度之和。

速度向量

在上一章中，我们通过计算位置函数相对于时间的导数得出了瞬时速度。我们可以在二维和三维上做同样的运算，但我们使用向量。瞬时速度矢量现在为

\[\vec{v} (t) = \lim_{\Delta t \rightarrow 0} \frac{\vec{r} (t + \Delta t) - \vec{r} (t)}{\Delta t} = \frac{d \vec{r}}{dt} \ldotp \label{4.4}\]

让我们以图形方式看一下位置向量和速度矢量的相对方向。在图中，$\PageIndex{6}$我们显示了向量$\vec{r}$$\vec{r}$ (t) 和 ($\Delta$t + t)，它们给出了粒子沿着由灰线表示的路径移动的位置。当$\Delta$ t 变为零时，由方程\ ref {4.4} 给出的速度矢量在时间 t 处与粒子的路径相切。

t 的向量 r 和 t 的 r 加上增量 t 在 x y 坐标系中显示为红色箭头。两个向量都从原点开始。向量 delta r 从 t 的向量 r 的头部指向 t 的向量 r 的头部加上 delta t。 — 图$\PageIndex{6}$：粒子沿着灰线给定的路径移动。在极限中，当$\Delta$ t 接近零时，速度矢量与粒子的路径相切。

方程\ ref {4.4} 也可以用$\vec{v}$ (t) 的分量来编写。由于

\[\vec{r} (t) = x(t)\; \hat{i} + y(t)\; \hat{j} + z(t)\; \hat{k},\]

我们可以写

\[\vec{v} (t) = v_{x} (t)\; \hat{i} + v_{y} (t)\; \hat{j} + v_{z} (t)\; \hat{k} \label{4.5}\]

哪里

\[v_{x} (t) = \frac{dx(t)}{dt}, \quad v_{y} (t) = \frac{dy(t)}{dt}, \quad v_{z} (t) = \frac{dz(t)}{dt} \ldotp \label{4.6}\]

如果只关注平均速度，则我们得到的矢量等效于二维和三维的一维平均速度：

\[\vec{v}_{avg} = \frac{\vec{r} (t_{2}) - \vec{r} (t_{1})}{t_{2} - t_{1}} \ldotp \label{4.7}\]

示例 4.3：计算速度矢量

粒子的位置函数为$\vec{r}$ (t) = 2.0t ²$\hat{i}$ + (2.0 + 3.0t)$\hat{j}$ + 5.0t$\hat{k}$ m。(a) t = 2.0 秒时的瞬时速度和速度是多少？ (b) 1.0 秒到 3.0 秒之间的平均速度是多少？

解决方案

使用方程\ ref {4.5} 和方程\ ref {4.6}，并取位置函数相对于时间的导数，我们发现

$$v (t) =\ frac {d\ vec {r} (t)} {dt} = 4.0t\;\ hat {i} + 3.0\;\ hat {j} + 5.0\;\ hat {k}\; m/s$$$\ vec {v} (2.0\; s) = 8.0\;\ hat {j} + 3.0\;\ hat {j} +;\ hat {k}\; m/s$$$speed\; |\ vec {v} (2.0\; s) | =\ sqrt {8^ {2} + 3^ {2} + 5^ {2}} = 9.9\; m/s\ ldotp$$
来自方程\ ref {4.7}，$$\ begin {split}\ vec {v} _ {avg} & =\ frac {\ vec {r} (t_ {2})-\ vec {r} (t_ {1})} =\ frac {\ vec {r} (3.0\; s)-\ vec {r} (1.0\; s)} {3.0\; s-1.0\; s} =\ frac {(18\;\ hat {i} + 11\;\ hat {j} + 15\;\ hat {k} + 5\;\ hat {k}) m} {2.0\; s}\\\\ frac {(16\;\ hat {i} + 6\;\ hat {j} + 10\;\ hat {k}) m} {2.0\; s} = 8.0\;\ hat {i} + 3.0\;\ hat {j} + 5.0\;\ hat {k}\; m/s\ ldotp\ end {split} $$

意义

我们看到平均速度与t = 2.0 s时的瞬时速度相同，这是因为速度函数是线性的。总的来说，情况不一定如此。实际上，在大多数情况下，瞬时速度和平均速度并不相同。

练习 4.1

粒子的位置函数为$\vec{r}$ (t) = 3.0t ³$\hat{i}$ + 4.0$\hat{j}$。 (a) t = 3 s 时的瞬时速度是多少？ (b) 2 秒到 4 秒之间的平均速度是否等于 t = 3 秒时的瞬时速度？

垂直运动的独立性

当我们查看以单位向量表示法书写的位置和速度的三维方程，即方程\ ref {4.2} 和方程\ ref {4.5} 时，我们会发现这些方程的分量是独立且唯一的时间函数，彼此不相关。沿 x 方向的运动不属于其沿 y 和 z 方向的运动，其他两个坐标轴也是如此。因此，可以将物体的二维或三维运动分为沿着运动发生的坐标系的垂直轴的独立运动。

为了说明这个与流离失所有关的概念，假设一个妇女在有方块的城市中从A点走到B点。走从 A 到 B 路径的女性可能会向东走这么多街区，然后向北（两个垂直方向），再走一组方块到达 B。她向东走多远只受她向东移动的影响。同样，她向北走多远只受她向北运动的影响。

运动的独立性

在运动学描述中，我们可以分别处理运动的水平和垂直分量。在许多情况下，水平方向的运动不会影响垂直方向的运动，反之亦然。

两个棒球给出了一个说明垂直和水平运动独立性的例子。一个棒球从静止状态中掉下来。同时，另一个从相同的高度水平投掷，然后沿着弯曲的路径行驶。闪光镜在球落下时以固定的时间间隔捕获其位置（图$\PageIndex{7}$）。

两个相同的球以相等的时间间隔显示在 5 个位置。球从相同的垂直位置开始。绿色箭头表示水平速度，紫色箭头表示每个位置的垂直速度。右边的球有初始水平速度，而左边的球没有水平速度。两个球的水平运动始终是恒定的水平速度。垂直运动是恒定的垂直加速度。每个球的垂直速度的幅度都在增加，并且指向下方。在每个时刻，两个球都有相同的垂直位置和垂直速度。 — 图$\PageIndex{7}$：两个相同球的运动示意图：一个从静止位置掉下来，另一个具有初始水平速度。随后的每个位置都是一个相等的时间间隔。箭头表示每个位置的水平和垂直速度。右边的球有初始水平速度，而左边的球没有水平速度。尽管水平速度不同，但两个球的垂直速度和位置是相同的，这表明垂直和水平运动是独立的。

值得注意的是，每次闪光灯闪烁，两个球的垂直位置都是一样的。这种相似性意味着垂直运动与球是否水平移动无关。（假设没有空气阻力，坠落物体的垂直运动仅受重力影响，不受任何水平力影响。）仔细检查水平投掷的球会发现它在两次闪光之间移动的水平距离相同。这是因为投掷球后，球在水平方向上没有额外的力。这个结果意味着水平速度是恒定的，既不受垂直运动的影响，也不受重力（垂直）的影响。请注意，这种情况仅适用于理想条件。在现实世界中，空气阻力会影响球的双向速度。

水平投掷球的二维曲线路径由两个独立的一维运动（水平和垂直）组成。分析这种运动（称为弹丸运动）的关键是将其解析为沿垂直方向的运动。将二维运动分解为垂直分量是可能的，因为这些分量是独立的。