45.3：人口增长的环境极限

培养技能

• 解释指数和逻辑增长模式的特征和区别
• 举例说明自然种群的指数和逻辑增长
• 描述自然选择和环境适应是如何导致特定生活史模式演变的

尽管生活史总体上描述了人口的许多特征（例如其年龄结构）随着时间的推移而发生的变化，但人口生态学家使用各种方法对人口动态进行数学建模。 然后，可以使用这些更精确的模型来准确描述人口中发生的变化，更好地预测未来的变化。 由于缺乏预测能力，某些已经被接受了数十年的模型现在正在被修改甚至放弃，学者们正在努力创建有效的新模型。

指数级增长

查尔斯·达尔文在他的自然选择理论中受到了英国神职人员托马斯·马尔萨斯的极大影响。 马尔萨斯在1798年出版了一本书，指出拥有无限自然资源的人口增长非常迅速，然后随着资源的枯竭，人口增长会降低。 这种人口规模增长的加速模式被称为指数增长。

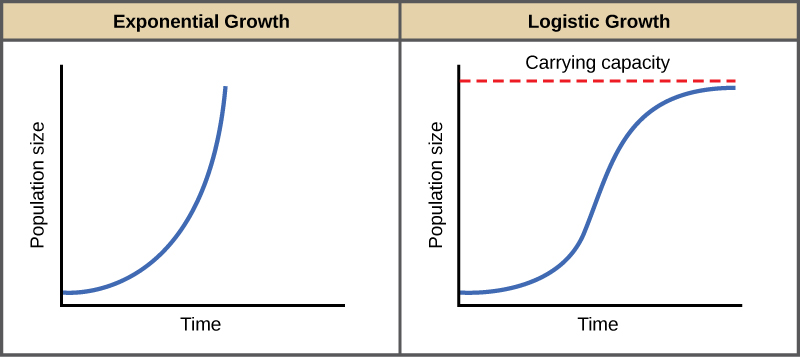
指数增长的最好例子是细菌。 细菌是通过原核裂变繁殖的原核生物。 对于许多细菌物种，这种分裂大约需要一个小时。 如果将1000个细菌放在一个有无限量营养素供应的大瓶中（这样营养素就不会耗尽），那么一小时后，就会出现一轮分裂，每个生物分裂，从而产生2000个生物——增加了1000个。 再过一个小时，2000个生物中的每一个都将翻一番，产生4000个，增加2000个。 第三个小时后，烧瓶中应该有 8000 个细菌，增加了 4000 个生物。 指数增长的重要概念是，种群增长率（每个繁殖世代中增加的生物数量）正在加速；也就是说，它正在以越来越快的速度增长。 经过1天零24个周期，人口将从1,000增加到超过160亿。 随着时间的推移绘制人口规模 N 时，会产生 J 形的增长曲线（图\(\PageIndex{1}\)）。

图\(\PageIndex{1}\)：当资源无限时，人口呈指数增长，由此形成 J 形曲线。 当资源有限时，人口会出现逻辑增长。 在物流增长中，随着资源稀缺，人口扩张减小，当环境承载能力达到时，人口增长趋于平稳，形成S形曲线。

细菌的例子不能代表资源有限的现实世界。 此外，一些细菌会在实验过程中死亡，因此无法繁殖，从而降低生长速度。 因此，在计算种群的增长率时，从出生率（B）（在该间隔内出生的生物数量）中减去死亡率（D）（在特定时间间隔内死亡的生物数量）。 如下面的公式所示：

\[\frac{\Delta N\;(\text{change in number})} {\Delta T\;(\text{change in time})} = B\;(\text{birth rate}) - D\;(\text{death rate}) \nonumber\]

出生率通常以人均（每个人）为基础表示。 因此，B（出生率）= b N（人均出生率 “b” 乘以个体数量 “N”），D（死亡率）= dN（人均死亡率 “d” 乘以个体数量 “N”）。 此外，生态学家对特定时间点（无限小的时间间隔）的人口感兴趣。 出于这个原因，使用微分微积分的术语来获得 “瞬时” 增长率，用特定于瞬间的数字和时间测量取代数字和时间的变化。

\[\frac{d N} {d T} = bN - dN = (b - d)N \nonumber\]

请注意，与第一个术语相关的 “d” 是指导数（因为该术语用于微积分），与死亡率（也称为 “”）不同\(d\)。 通过用 “r”（固有增长率）代替出生率和死亡率之间的关系，进一步简化了出生率和死亡率之间的差异：

\[\frac{d N} {d T} = rN \nonumber\]

值 “\(r\)” 可以是正数，表示人口规模正在增加；也可以是负值，表示人口规模正在缩小；也可以为零，表示人口规模不变，这种情况称为人口零增长。 对该公式的进一步完善认识到，即使在理想条件下，不同物种的固有增长率（通常被认为是繁殖潜力）也有固有的差异。 显然，与人类相比，细菌可以更快地繁殖并具有更高的固有生长速度。 一个物种的最大生长速度是其生物潜力，或者\(r_{max}\)，因此将方程改为：

\[\frac{d N} {d T} = r_\text{max}N \nonumber\]

物流增长

只有当无限的自然资源可用时，才有可能实现指数级增长；在现实世界中情况并非如此。 查尔斯·达尔文在他对 “为生存而斗争” 的描述中承认了这一事实，该描述指出，个人将（与自己或其他物种的成员）争夺有限的资源。 成功的人将存活下来，以更快的速度（自然选择）将自己的特征和特征（我们知道这些特征和特质是通过基因转移的）传给下一代。 为了模拟资源有限的现实，人口生态学家开发了逻辑增长模型。

承载能力和物流模型

在现实世界中，资源有限，指数级增长不可能无限期地持续下去。 在个人很少且资源充足的环境中可能会出现指数级增长，但是当个人数量变得足够多时，资源就会耗尽，从而减缓增长速度。 最终，增长率将稳定或趋于平稳（图\(\PageIndex{1}\)）。 这种人口规模代表特定环境可以支持的最大人口规模，称为承载能力或\(K\)。

我们用来计算物流增长的公式将承载能力作为增长率的调节力相加。 “\(K – N\)” 一词表示在给定阶段可以向人口中添加多少人，而 “\(K – N\)” 除以 “\(K\)” 是可用于进一步增长的承载能力的比例。 因此，指数增长模型受此因子的限制，无法生成逻辑增长方程：

\ [\ begin {align}\ dfrac {d N} {d T}
&= r_\ text {max}\ frac {d N} {d T}\ nonumber\ [5pt]
&= r_\ text {max} N\ frac {(K-N)} {K}\ nonumber
\ end {align}\ nonumber\]

请注意，当\(N\)非常小时，\((K-N)/K\)变为接近\(K/K\)或\(1\)，方程的右侧缩小为\(r_{max}N\)，这意味着人口呈指数级增长，不受承载能力的影响。 另一方面，如果人口较大，\(N\)则\((K-N)/K\)接近于零，这意味着人口增长将大大放缓甚至停止。 因此，承载能力大大减缓了大量人口的人口增长\(K\)。 该模型还允许人口出现负增长或人口减少。 当人口中的个体数量超过承载能力时（因为的值为负），就会发生\((K-N)/K\)这种情况。

该方程的图形生成了一条 S 形曲线（图\(\PageIndex{1}\)），与指数增长相比，它是更真实的人口增长模型。 S 形曲线有三个不同的部分。 最初，增长呈指数级增长，因为可用的人很少，资源充足。 然后，随着资源开始变得有限，增长率降低。 最后，增长在环境的承载能力上趋于平稳，随着时间的推移，人口规模变化不大。

种内竞争的作用

逻辑模型假设人口中的每个人都有平等的机会获得资源，因此有平等的生存机会。 对于植物来说，水量、阳光、养分和生长空间是重要的资源，而在动物中，重要的资源包括食物、水、庇护所、筑巢空间和伴侣。

在现实世界中，人群中个体之间的表型差异意味着有些人比其他人更能适应环境。 由此产生的同一物种的种群成员之间对资源的竞争被称为种内竞争（intra-= “内部”；specialic = “物种”）。 种内对资源的竞争可能不会影响远低于其承载能力的人群——资源丰富，所有人都能获得他们所需要的东西。 但是，随着人口规模的增加，这种竞争加剧。 此外，废物的积累会降低环境的承载能力。

物流增长的例子

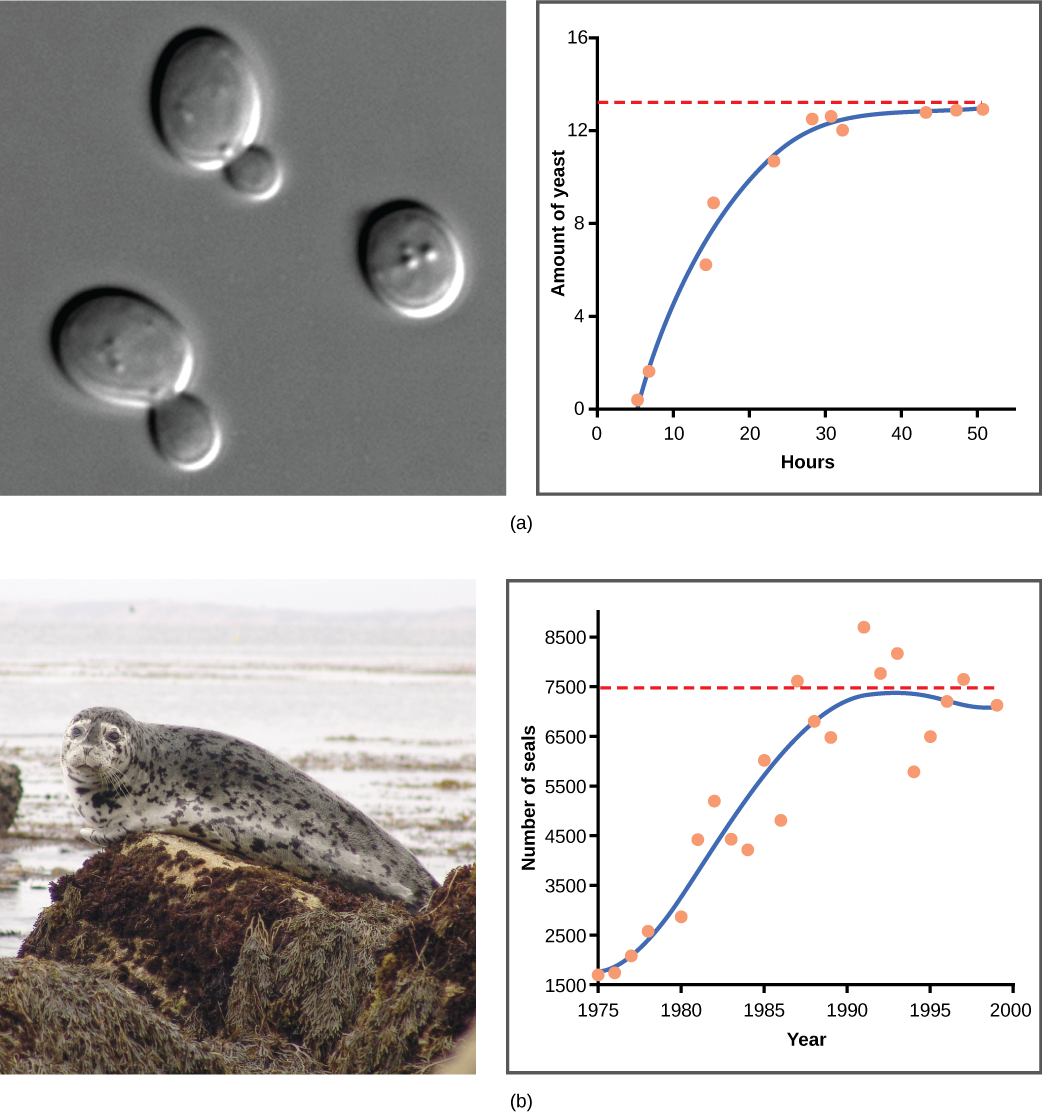
酵母是一种用于制作面包和酒精饮料的微观真菌，在试管中生长时呈现出经典的 S 形曲线（图\(\PageIndex{2}\) a）。 随着人口消耗其生长所必需的营养，其增长趋于平稳。 但是，在现实世界中，这条理想化的曲线存在变化。 野生种群中的例子包括绵羊和海豹（图\(\PageIndex{2}\) b）。 在这两个例子中，人口规模在短时间内超过承载能力，然后降至承载能力以下。 随着人口围绕其承载能力波动，人口规模的这种波动继续发生。 尽管如此，即使出现了这种振荡，逻辑模型还是得到了证实。

艺术连接

图\(\PageIndex{2}\)：（a）在理想条件下在试管中生长的酵母显示了经典的S形逻辑生长曲线，而（b）海豹的自然种群显示了现实世界的波动。

如果海豹的主要食物来源因污染或过度捕捞而减少，可能会发生以下哪种情况？

1. 海豹的承载能力将降低，海豹数量也会降低。
2. 海豹的承载能力会降低，但海豹的数量将保持不变。
3. 海豹死亡人数将增加，但出生人数也会增加，因此种群规模将保持不变。
4. 海豹的承载能力将保持不变，但海豹的数量将减少。

摘要

拥有无限资源的人口呈指数级增长，增长速度加快。 当资源变得有限时，人口会遵循逻辑增长曲线。 一个物种的种群将在其环境的承载能力上趋于平稳。

艺术联系

图\(\PageIndex{2}\) b 如果海豹的主要食物来源因污染或过度捕捞而减少，可能会发生以下哪种情况？

1. 海豹的承载能力将降低，海豹数量也会降低。
2. 海豹的承载能力会降低，但海豹的数量将保持不变。
3. 海豹死亡人数将增加，但出生人数也会增加，因此种群规模将保持不变。
4. 海豹的承载能力将保持不变，但海豹的数量将减少。

回答

一个

词汇表

生物潜力 (r _max)

物种的最大潜在生长速度

出生率 (B)

人口中在特定时间点的出生人数

承载能力 (K)

可以由栖息地有限资源支持的物种的个体数量

死亡率 (D)

人口中在特定时间点的死亡人数

指数级增长

在资源不受限制的条件下，物种的生长模式正在加速

种内竞争

同一物种的成员之间的竞争

J 形增长曲线

指数增长曲线的形状

物流增长

由于资源有限，指数级增长趋于平稳

人口增长率

每个繁殖世代中添加的生物数量

S 形增长曲线

逻辑增长曲线的形状

人口零增长

在出生率和死亡率相等的情况下稳定的人口规模