Skip to main content
Global

12.1: 孟德尔实验和概率定律

  1. Last updated
  2. Save as PDF
  • Page ID
    202906

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    培养技能

    • 描述孟德尔实验工作成功的科学原因
    • 描述涉及显性等位基因和隐性等位基因的单杂交杂交的预期结果
    • 应用总和和和乘积规则来计算概率

    约翰·格雷戈尔·孟德尔（1822-1884）（图\(\PageIndex{1}\)）是一位终身学习者、教师、科学家和有信仰的人。 年轻时，他加入了位于现在的捷克共和国布尔诺的圣托马斯奥古斯丁修道院。 在修道院的支持下，他在中学和大学阶段教授物理、植物学和自然科学课程。 1856年，他开始了长达十年的研究，涉及蜜蜂和植物的遗传模式，最终选择豌豆植物作为他的主要模型系统（一种具有便捷特征的系统，用于研究应用于其他系统的特定生物现象）。 1865 年，孟德尔向当地自然历史学会展示了他对近 30,000 株豌豆植物的实验结果。 他证明了特质是从父母忠实地传给后代的，不受其他特征的影响，并以显性和隐性模式传播。 1866年，他在布伦自然历史学会会刊上发表了他的著作《植物杂交实验》1。

    格雷戈尔·孟德尔的素描，一个戴着老花镜和一个大十字架的僧侣。
    图\(\PageIndex{1}\)：约翰·格雷戈尔·孟德尔被认为是遗传学之父。

    孟德尔的作品几乎没有被科学界注意到，他们错误地认为遗传过程涉及父母特征的混合，从而在后代中产生中间的外观；这个假设的过程似乎是正确的，因为我们现在所知道的连续变化。 持续变异源于许多基因在确定人类身高等特征方面的作用。 当我们观察表现出持续变化的特征时，后代似乎是其父母特征的 “混合体”。 混合遗传理论断言，原始的亲本特征被后代的混合所消失或吸收，但我们现在知道事实并非如此。 孟德尔是第一个看到它的研究人员。 孟德尔不是连续的特征，而是使用不同类别中继承的特征（特别是紫花与白花）；这被称为不连续变异。 孟德尔对这类特征的选择使他能够通过实验看出，这些特征没有融入后代中，也没有被吸收，而是保持了自己的独特性并且可以传播。 1868 年，孟德尔成为修道院的住持，将他的科学追求换成了牧师职责。 他一生中非凡的科学贡献没有得到认可。 事实上，直到1900年，他的作品才被即将发现遗传染色体基础的科学家重新发现、复制和振兴。

    孟德尔的模型系统

    孟德尔的开创性工作是使用花园豌豆 P isum sativum 来研究遗传学完成的。 该物种自然会自我受精，因此花粉在单朵花中会遇到卵子。 花瓣在授粉之前一直保持密封状态，防止其他植物授粉。 结果是豌豆植物高度近交或 “真繁殖”。 这些植物总是会产生看起来像亲本的后代。 通过尝试真正繁殖的豌豆植物，孟德尔避免了后代出现意想不到的特征，如果这些植物不是真正的繁殖则可能出现这种特征。 园豌豆也可以在一个季节内长成熟，这意味着可以在相对较短的时间内评估几代人。 最后，可以同时种植大量的豌豆，这使孟德尔得出结论，他的结果并非偶然产生。

    孟德尔十字架

    孟德尔进行了杂交，包括交配两个具有不同特征的真正繁殖个体。 在自然自授粉的豌豆中，这是通过手动将花粉从一个品种的成熟豌豆植物的花药转移到第二个品种的单独成熟豌豆植物的柱头上来完成的。 在植物中，花粉将雄配子（精子）带到柱头，柱头是一种粘性器官，可以捕获花粉并允许精子沿雌蕊向下移动到下面的雌配子（卵子）。 为了防止接受花粉的豌豆植物自我受精并混淆其结果，孟德尔在植物花朵有机会成熟之前精心地将所有花药从植物花朵中取出。

    第一代杂交中使用的植物被称为 P 0，或第一代亲本植物（图\(\PageIndex{2}\)）。 孟德尔收集了来自每个杂交种的P 0 植物的种子，并在下一个季节种植它们。 这些后代被称为 F 1 或第一代（孝顺 = 后代、女儿或儿子）。 孟德尔研究了F 1 代植物的特征后，他允许它们自然地自我受精。 然后，他收集并种植了 F 1 植物的种子，以生产 F 2 或第二代。 孟德尔的实验从 F 2 一代延伸到 F 3 和 F 4 代，依此类推，但最吸引人的是 P 0 −F 1 −F 2 代的特征比率，并成为孟德尔的假设。

    该图显示了真正繁殖紫色花色的豌豆植物和真正繁殖白花颜色的豌豆植物之间的交叉。 P 世代的这种交叉受精产生了 F_ {1} 一代，全是紫罗兰花。 F_ {1} 一代的自我受精产生了 F_ {2} 代，其中包括 705 株有紫罗兰花的植物和 224 株有白花的植物。
    图\(\PageIndex{2}\)：在他的一项遗传模式实验中，孟德尔将真正育种紫罗兰花颜色的植物与真正育种白花颜色（P 代）的植物交叉在一起。 由此产生的F 1 代杂交种都有紫罗兰花。 在 F 2 世代中，大约四分之三的植物有紫罗兰花，四分之一的植物有白花。

    Garden Pea 的特征揭示了遗传的基础

    孟德尔在1865年的出版物中报道了他的十字架的结果，这些交叉涉及七个不同的特征，每个特征都有两个截然不同的特征。 特征被定义为可遗传特征的物理外观的变化。 特征包括植物高度、种子质地、种子颜色、花朵颜色、豌豆荚大小、豌豆荚颜色和花位置。 例如，就花色的特征而言，两个截然不同的特征是白色和紫罗兰色。 为了全面检查每个特征，孟德尔生成了大量的 F 1 和 F 2 植物，仅报告了 19,959 个 F 2 植物的结果。 他的发现是一致的。

    孟德尔在他的花朵颜色十字架上发现了什么结果？ 首先，孟德尔证实他的植物是真正繁殖出来的白色或紫罗兰色花朵颜色。 不管孟德尔考察了多少代，所有养着白花的父母的自我交叉后代都有白花，而所有有紫罗兰花的父母的自我交叉后代都有紫罗兰花。 此外，孟德尔证实，除了花的颜色外，豌豆植物在物理上是相同的。

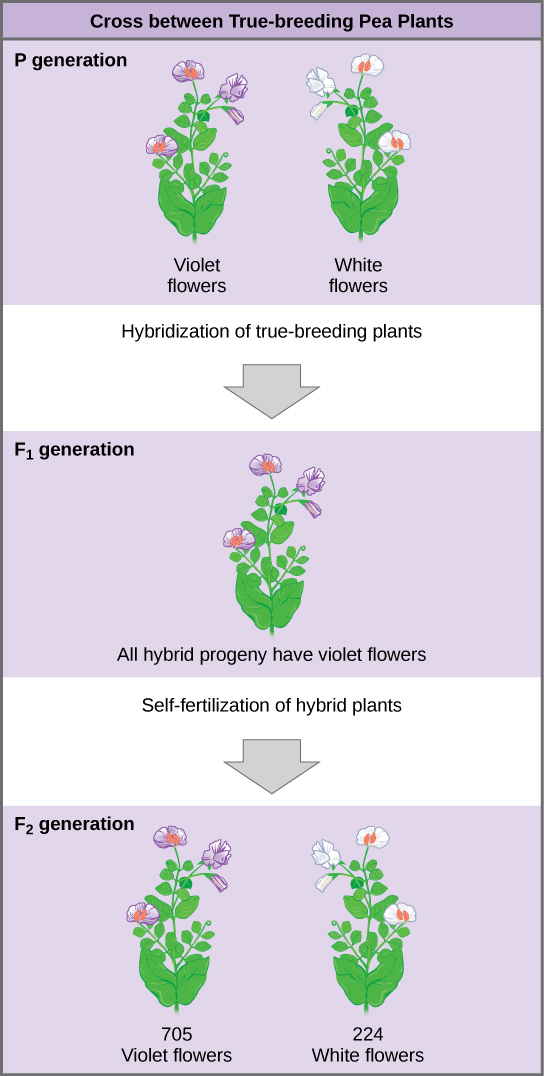
    这些验证完成后，孟德尔将紫罗兰花植物的花粉涂在有白花的植物的柱头上。 孟德尔在收集并播种了这个杂交产生的种子后，发现F 1 杂交一代中有100％有紫罗兰花。 当时的传统观点本来可以预测杂交花是淡紫罗兰色，或者杂交植物会有相等数量的白花和紫罗兰花。 换句话说，对比鲜明的父母特征有望融入后代中。 相反，孟德尔的结果表明，F 1 一代的白花特征已经完全消失了。

    重要的是，孟德尔并没有在那里停止他的实验。 他允许 F 1 植物自我受精，发现 F 2 代植物中，705 株有紫罗兰花，224 朵有白花。 这个比例为每朵白花3.15朵紫罗兰花，约为 3:1。 当孟德尔将花粉从有紫罗兰花的植物转移到有白花的植物的柱头上时，反之亦然，无论哪个亲本，雄性还是雌性贡献了哪个特征，他都获得了大致相同的比例。 这就是所谓的互惠十字架 ——一种成对的十字架，其中一个十字架中雄性和雌性的各自特征成为另一个十字架中雌性和雄性的各自特征。 对于孟德尔研究的其他六个特征，F 1 和 F 2 世代的行为与花的颜色相同。 这两个特征中的一个将从 F 1 世代中完全消失，然后以大约 3:1 的比例重新出现在 F 2 世代中（表\(\PageIndex{1}\)）。

    表\(\PageIndex{1}\)：孟德尔花园豌豆杂交的结果
    特点 对比 P 0 特征 F 1 后代特征 F 2 后代特征 F 2 特质比率
    花的颜色 紫罗兰色与白色 百分之百紫罗兰色
    • 705 紫罗兰色
    • 224 白色
    		 3. 15:1
    花的位置 轴向与终端 百分之百轴向
    • 651 轴向
    • 207 航站楼
    		 3. 14:1
    植物高度 高大与矮人 百分之百高
    • 身高 787
    • 277 矮人
    		 2. 84:1
    种子纹理 圆形与有皱纹的对比 百分之百回合
    • 5,474 回合
    • 1,850 起皱了
    		 2. 96:1
    种子颜色 黄色与绿色 百分之百是黄色
    • 6,022 黄色
    • 2,001 绿色
    		 3. 01:1
    豌豆荚纹理 膨胀与收缩 百分之百膨胀
    • 882 充气了
    • 299 收缩了
    		 2. 95:1
    豌豆荚颜色 绿色与黄色 百分之百绿色
    • 428 绿色
    • 152 黄色
    		 2. 82:1

    孟德尔在汇编了成千上万株植物的结果后得出结论，这些特征可以分为表现性状和潜在特征。 他分别称这些为显性特征和隐性特征。 显性特征是那些在杂交过程中遗传不变的特征。 隐性特征在杂交的后代中变得潜伏或消失。 但是，隐性特征确实在杂交后代的后代中重新出现。 显性特征的一个例子是紫罗兰花特征。 对于同样的特征（花的颜色），白色花是一种隐性特征。 隐性性状在 F 2 代中重新出现的事实意味着这些性状在 F 1 代植物中仍然是分离的（不是混合）。 孟德尔还提出，植物具有两个花色特征的副本，每个亲本将其两个副本中的一个传递给其后代，然后它们聚集在一起。 此外，对显性特征的物理观察可能意味着该生物体的遗传组成包括该特征的两个显性版本，或者它包括一个显性版本和一个隐性版本。 相反，观察到隐性特征意味着该生物体缺乏这种特征的任何显性版本。

    那么，为什么孟德尔在十字架上反复获得 3:1 的比率呢？ 要理解孟德尔是如何推断出导致这种比率的基本继承机制的，我们必须首先回顾概率定律。

    概率基础知识

    概率是可能性的数学度量。 事件的经验概率是通过将事件发生的次数除以事件发生的机会总数来计算的。 也可以通过将一个事件预计发生的次数除以该事件可能发生的次数来计算理论概率。 经验概率来自观测结果，例如孟德尔的观测结果。 理论概率来自于了解事件是如何产生的，并假设个体结果的概率是相等的。 某些事件的概率为 1 表示它一定会发生，而概率为零表示保证不会发生。 遗传事件的一个例子是豌豆植物产生的圆形种子。 孟德尔在实验中证明，“圆形种子” 事件发生的概率是真正繁殖亲本的F 1 后代中的一个，其中一个有圆形种子，另一个有皱纹的种子。 当 F 1 植物随后自我交叉时，任何给定的 F 2 后代获得圆形种子的概率现在为四分之三。 换句话说，在随机选择的大量F 2 后代中，预计有75％的后代会有圆形种子，而25％的后代预计会有皱纹的种子。 使用大量交叉盘，孟德尔得以计算概率并使用这些概率来预测其他交叉的结果。

    乘积规则和总和规则

    孟德尔证明，他研究的豌豆植物特征是作为离散单位从父母传给后代的。 正如将要讨论的那样，孟德尔还确定，不同的特征，例如种子颜色和种子质地，是相互独立传播的，可以在单独的概率分析中考虑。 例如，在种子呈绿色、有皱纹的植物和种子为黄色圆形的植物之间进行杂交，所产生的后代的绿黄种子比例为 3:1（忽略种子质地），圆形：皱纹种子的比例为 3:1（忽略种子颜色）。 颜色和纹理的特征没有相互影响。

    概率乘积法则可以应用于这种特征独立传输的现象。 乘积规则指出，两个独立事件一起发生的概率可以通过将每个事件单独发生的概率相乘来计算。 为了演示乘积法则，假设你在滚动一个六面骰子（D），同时翻一分钱（P）。 骰子可以掷出 1—6（D #）中的任意数字，而一分钱可以向上翻正面（P H）或反面（P T）。 掷骰子的结果对翻转一分钱的结果没有影响，反之亦然。 此操作有 12 种可能的结果（表\(\PageIndex{2}\)），每个事件的发生概率相等。

    表\(\PageIndex{2}\)：掷骰子和翻一分钱的十二种同样可能的结果
    轧模 翻转一分钱
    D 1 P H
    D 1 P T
    D 2 P H
    D 2 P T
    D 3 P H
    D 3 P T
    D 4 P H
    D 4 P T
    D 5 P H
    D 5 P T
    D 6 P H
    D 6 P T

    在12种可能的结果中，骰子的掷出二的概率为2/12（或1/6），而一分钱的上升概率为6/12（或1/2）。 根据乘积规则，你获得组合结果 2 和正面的概率为：(D 2) x (P H) = (1/6) x (1/2) 或 1/12（上表）。 注意概率描述中的 “and” 一词。 “and” 是应用产品规则的信号。 例如，考虑如何将乘积法则应用于 dihybrid 十字架：F 2 后代中具有两个显性特征的概率是每个特征具有显性特征的概率的乘积，如下所示：

    \[\frac{3}{4} * \frac{3}{4} = \frac{9}{16}\nonumber\]

    另一方面，在考虑可能由多个途径产生的两个相互排斥的结果时，应用概率总和规则。 总和规则指出，两个相互排斥的事件发生一个事件或另一个事件的概率是它们各自概率的总和。 注意概率描述中的 “或” 一词。 “或” 表示您应该应用总和规则。 在这种情况下，假设你在翻转一分钱（P）和四分之一（Q）。 一枚硬币上升而一枚硬币倒在后面的概率是多少？ 这个结果可以通过两种情况来实现：一分钱可能是正面（P H），季度可能是倒数（Q T），或者季度可能是正面（Q H），一分钱可能是倒数（P T）。 无论哪种情况都符合结果。 根据总和规则，我们将获得一个头和一个尾巴的概率计算为

    \[\mathrm{[(P_H) × (Q_T)] + [(Q_H) × (P_T)] = [(1/2) × (1/2)] + [(1/2) × (1/2)] = 1/2.}\nonumber\]

    您还应该注意到，在我们对 P H 和 Q T 进行求和之前，我们使用乘积法则来计算 P T 和 Q H 的概率。 同样，可以应用总和规则来显示在双杂交叉的 F 2 代中只有一个显性特征的概率：

    \[\frac{3}{16} + \frac{3}{4} = \frac{15}{16}\nonumber\]

    表\(\PageIndex{3}\)：乘积规则和总和规则
    产品规则 总和规则
    对于独立事件 A 和 B，它们同时发生（A 和 B）的概率（P）为（P A × P B） 对于互斥事件 A 和 B，至少发生一个（A 或 B）的概率 (P) 为 (P A + P B)

    要在实践中使用概率定律，必须使用较大的样本量，因为小样本量容易出现偶然造成的偏差。 孟德尔检查的大量豌豆植物使他能够计算出他的 F 2 世代中出现的特征的概率。 正如你将要学到的那样，这一发现意味着，当知道父母的特征时，甚至在受精之前就可以准确预测后代的特征。

    摘要

    孟德尔在研究园豌豆植物时发现，父母之间存在一个特征差异的杂交产生了 F 1 后代，这些后代都表达了亲本一方的性状。 可观察到的特征被称为显性特征，未表达的特征被描述为隐性特征。 当孟德尔实验中的后代自我交叉时，F 2 后代以 3:1 的比例表现出显性特征或隐性特征，这证实了隐性特征是从原始 P 0 亲本那里忠实传播的。 倒数交叉生成相同的 F 1 和 F 2 后代比率。 通过研究样本量，孟德尔表明，根据概率定律，他的十字架行为是可重复的，并且这些特征是作为独立事件继承的。

    两条概率规则可用于找出来自不同十字架的具有不同特征的后代的预期比例。 要计算两个或更多个独立事件一起发生的概率，请应用乘积规则并将各个事件的概率相乘。 使用 “和” 一词表明产品规则的适当适用。 要计算两个或多个事件组合发生的概率，请应用求和规则并将它们的各个概率相加。 使用 “或” 一词表明总和规则的适当适用。

    脚注

    1. 1 Johann Gregor Mendel，Versuche 关于巴达州布伦的 PflanzenHybriden Verhandlungen des naturforschenden Vereines IV for das Jahr，1865 年 Abhandlungen，3—47。 [有关英文翻译，请参阅 www.mendelWeb.org/mendel.plain.html]

    词汇表

    混合继承理论
    假设的遗传模式，在这种模式中，父母特征在后代中混合在一起，产生中间的外观
    连续变化
    继承模式，在这种模式中，角色显示一系列特征值，这些值之间的渐变较小而不是较大的间隙
    不连续变化
    遗传模式，其中特征各不相同，相互独立传播
    占主导地位的
    无论一个人有两个特征副本还是一个显性特征副本和一个隐性特征副本，它都具有相同的外观
    F 1
    十字架上的第一代孝顺一代；父母一代的后代
    F 2
    当 F 1 个体自我交叉或相互受精时产生的第二代孝顺子
    杂交
    交配两个不同的个体的过程，目的是在他们的后代中实现某种特征
    模型系统
    用于研究特定生物现象的物种或生物系统，应用于其他不同物种
    P 0
    十字架上的父母一代
    产品规则
    两个独立事件同时发生的概率可以通过将每个事件单独发生的概率相乘来计算
    隐性
    当个体也具有相同特征的显性特征时出现 “潜伏” 或未表达的特征；当以两个相同的副本存在时，隐性特征被表达
    倒数交叉
    配对十字架，其中一个十字架中雄性和雌性的各自特征成为另一个十字架中雌性和雄性的各自特征
    总和规则
    两个相互排斥的事件中至少出现一个的概率是它们各自概率的总和
    特征
    可遗传特征的物理外观变化