Skip to main content
Global

7.4: 解决问题

  1. Last updated
  2. Save as PDF
  • Page ID
    203382

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    • 描述问题解决策略
    • 定义算法和启发式
    • 解释有效解决问题的一些常见障碍

    人们每天都面临问题——通常，一天中有多个问题。 有时候这些问题很简单：例如，要将披萨面团的配方加倍，只需要将食谱中的每种成分加倍。 但是，有时我们遇到的问题更为复杂。 例如，假设你有工作截止日期，你必须在工作日结束前将报告的打印副本邮寄给你的主管。 该报告具有时间敏感性，必须在一夜之间发送。 你昨晚完成了报告，但你的打印机今天无法正常工作。 你应该怎么做？ 首先，你需要确定问题，然后应用解决问题的策略。

    问题解决策略

    当你遇到问题时，无论是复杂的数学问题还是打印机损坏，你是如何解决这个问题的？ 在找到问题的解决方案之前，必须首先清楚地确定问题。 之后，可以应用许多问题解决策略中的一种，希望能找到解决方案。

    解决问题的策略是用于寻找解决方案的行动计划。 不同的策略有不同的相关行动计划（见\(\PageIndex{1}\)下表）。 例如，一个众所周知的策略是反复试验。 古老的格言 “如果一开始你没有成功，那就试试，再试一次” 描述了反复试验。 就打印机损坏而言，你可以尝试检查墨水量，如果这不起作用，你可以检查以确保纸盒没有卡住。 或者打印机实际上并未连接到您的笔记本电脑。 使用反复试验时，你会继续尝试不同的解决方案，直到问题得到解决。 尽管反复试验通常不是最省时的策略之一，但它是一种常用的策略。

    表 \(\PageIndex{1}\)：问题解决策略
    方法 描述 示例
    反复试验 继续尝试不同的解决方案，直到问题得到解决 重启手机、关闭 WiFi、关闭蓝牙以确定手机出现故障的原因
    算法 分步解决问题的公式 在计算机上安装新软件的说明手册
    启发式 一般问题解决框架 向后工作；将任务分成几个步骤

    另一种策略是算法。 算法是一种解决问题的公式，它为您提供用于实现预期结果的分步说明（Kahneman，2011）。 你可以将算法看作是包含非常详细的指令的配方，每次执行时都会产生相同的结果。 算法在我们的日常生活中经常使用，尤其是在计算机科学中。 当你在互联网上进行搜索时，谷歌等搜索引擎会使用算法来决定哪些条目将首先出现在你的结果列表中。 Facebook 还使用算法来决定在你的新闻源上显示哪些帖子。 你能确定使用算法的其他情况吗？

    启发式方法是另一种解决问题的策略。 虽然必须严格遵循算法才能得出正确的结果，但启发式方法是一种通用的问题解决框架（Tversky & Kahneman，1974 年）。 你可以把这些看作是用来解决问题的心理捷径。 “经验法则” 就是启发式方法的一个例子。 这样的规则可以在人们做出决定时节省时间和精力，但是尽管它具有节省时间的特点，但它并不总是做出理性决策的最佳方法。 不同类型的启发式方法用于不同类型的情况，但是当满足五个条件之一时，就会产生使用启发式方法的冲动（Pratkanis，1989 年）：

    • 当一个人面对太多信息时
    • 当做出决定的时间有限时
    • 当要做的决定不重要时
    • 当在做出决策时获得的信息很少时
    • 当恰当的启发式方法在同一时刻浮现在脑海时

    向后工作是一种有用的启发式方法，在这种方法中，你可以通过关注最终结果来开始解决问题。 举这个例子：你住在华盛顿特区，受邀参加周六在费城\(\text{4 PM}\)举行的婚礼。 知道州际公路\(95\)往往会在一周中的任何一天进行备份，因此您需要计划路线并相应地安排出发时间。 如果你想参加婚礼服务\(\text{3:30 PM}\)，而且要花\(2.5\)几个小时才能在没有交通的情况下到达费城，那么你应该什么时候离开家？ 你使用向后工作的启发式方法来定期计划当天的事件，可能甚至没有考虑过。

    另一个有用的启发式方法是通过将大型目标或任务分解成一系列较小的步骤来完成该目标或任务。 学生经常使用这种常用的方法来完成大型研究项目或学校的长篇论文。 例如，学生通常集思广益，撰写论文或主要话题，研究所选主题，将他们的信息整理成大纲，撰写草稿，修改和编辑草稿，制定最终草稿，整理参考文献清单，并在上交项目之前校对他们的作品。 当将大型任务分解为一系列小步骤时，它就会变得不那么艰巨。

    EVERYDAY CONNECTION: Solving Puzzles

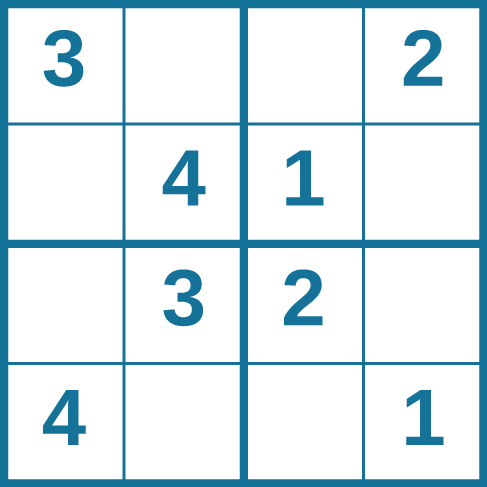
    Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a \(9\times 9\) grid. The simple sudoku below is a \(4\times 4\) grid. To solve the puzzle, fill in the empty boxes with a single digit: \(1\), \(2\), \(3\), or \(4\). Here are the rules: The numbers must total \(10\) in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.

    A four column by four row Sudoku puzzle is shown. The top left cell contains the number 3. The top right cell contains the number 2. The bottom right cell contains the number 1. The bottom left cell contains the number 4. The cell at the intersection of the second row and the second column contains the number 4. The cell to the right of that contains the number 1. The cell below the cell containing the number 1 contains the number 2. The cell to the left of the cell containing the number 2 contains the number 3.
    Figure \(\PageIndex{1}\): How long did it take you to solve this sudoku puzzle? (You can see the answer at the end of this section.)

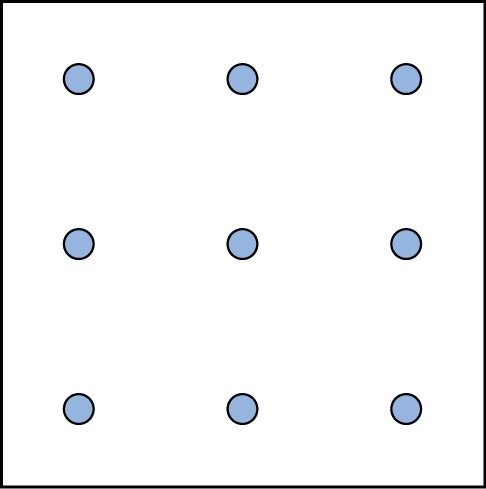
    Here is another popular type of puzzle that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:

    A square shaped outline contains three rows and three columns of dots with equal space between them.
    Figure \(\PageIndex{2}\): Did you figure it out? (The answer is at the end of this section.) Once you understand how to crack this puzzle, you won’t forget.

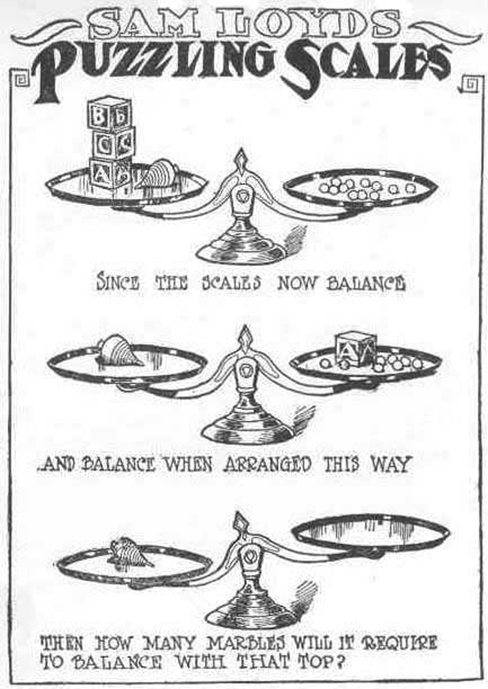
    Take a look at the “Puzzling Scales” logic puzzle below. Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).

    A puzzle involving a scale is shown. At the top of the figure it reads: “Sam Loyds Puzzling Scales.” The first row of the puzzle shows a balanced scale with 3 blocks and a top on the left and 12 marbles on the right. Below this row it reads: “Since the scales now balance.” The next row of the puzzle shows a balanced scale with just the top on the left, and 1 block and 8 marbles on the right. Below this row it reads: “And balance when arranged this way.” The third row shows an unbalanced scale with the top on the left side, which is much lower than the right side. The right side is empty. Below this row it reads: “Then how many marbles will it require to balance with that top?”
    Figure \(\PageIndex{3}\): What steps did you take to solve this puzzle? You can read the solution at the end of this section.

    Pitfalls to Problem Solving

    Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.

    Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.

    Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).

    In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of \(\$1,600\). The realtor shows you only very run-down houses for \(\$1,600\) and then shows you a very nice house for \(\$2,000\). Might you ask each person to pay more in rent to get the \(\$2,000\) home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.

    The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.

    Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision. Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in the Table \(\PageIndex{2}\) below.

    Table \(\PageIndex{2}\): Summary of Decision Biases
    Bias Description
    Anchoring Tendency to focus on one particular piece of information when making decisions or problem-solving
    Confirmation Focuses on information that confirms existing beliefs
    Hindsight Belief that the event just experienced was predictable
    Representative Unintentional stereotyping of someone or something
    Availability Decision is based upon either an available precedent or an example that may be faulty

    Were you able to determine how many marbles are needed to balance the scales in Figure \(\PageIndex{3}\)? You need nine.

    Were you able to solve the problems in Figure \(\PageIndex{1}\) and Figure \(\PageIndex{2}\)? Here are the answers:

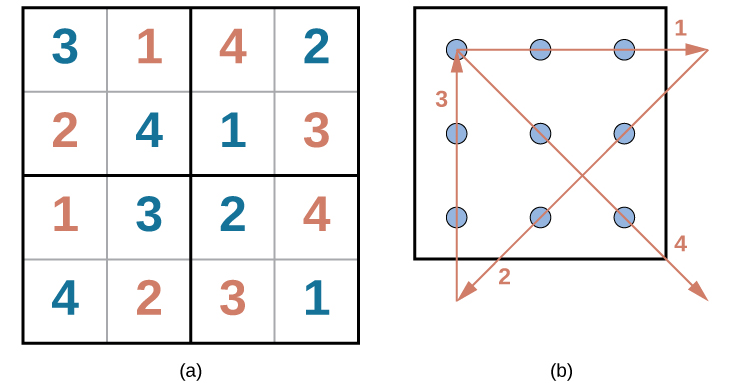
    The first puzzle is a Sudoku grid of 16 squares (4 rows of 4 squares) is shown. Half of the numbers were supplied to start the puzzle and are colored blue, and half have been filled in as the puzzle’s solution and are colored red. The numbers in each row of the grid, left to right, are as follows. Row 1: blue 3, red 1, red 4, blue 2. Row 2: red 2, blue 4, blue 1, red 3. Row 3: red 1, blue 3, blue 2, red 4. Row 4: blue 4, red 2, red 3, blue 1.The second puzzle consists of 9 dots arranged in 3 rows of 3 inside of a square. The solution, four straight lines made without lifting the pencil, is shown in a red line with arrows indicating the direction of movement. In order to solve the puzzle, the lines must extend beyond the borders of the box. The four connecting lines are drawn as follows. Line 1 begins at the top left dot, proceeds through the middle and right dots of the top row, and extends to the right beyond the border of the square. Line 2 extends from the end of line 1, through the right dot of the horizontally centered row, through the middle dot of the bottom row, and beyond the square’s border ending in the space beneath the left dot of the bottom row. Line 3 extends from the end of line 2 upwards through the left dots of the bottom, middle, and top rows. Line 4 extends from the end of line 3 through the middle dot in the middle row and ends at the right dot of the bottom row.

    Figure \(\PageIndex{4}\): Solutions to the puzzles in Everyday Connection

    Summary

    Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. Roadblocks to problem solving include a mental set, functional fixedness, and various biases that can cloud decision making skills.

    Glossary

    algorithm
    problem-solving strategy characterized by a specific set of instructions
    anchoring bias
    faulty heuristic in which you fixate on a single aspect of a problem to find a solution
    availability heuristic
    faulty heuristic in which you make a decision based on information readily available to you
    confirmation bias
    faulty heuristic in which you focus on information that confirms your beliefs
    functional fixedness
    inability to see an object as useful for any other use other than the one for which it was intended
    heuristic
    mental shortcut that saves time when solving a problem
    hindsight bias
    belief that the event just experienced was predictable, even though it really wasn’t
    mental set
    continually using an old solution to a problem without results
    problem-solving strategy
    method for solving problems
    representative bias
    faulty heuristic in which you stereotype someone or something without a valid basis for your judgment
    trial and error
    problem-solving strategy in which multiple solutions are attempted until the correct one is found
    working backwards
    heuristic in which you begin to solve a problem by focusing on the end result

    Contributors