持续的长期经济增长来自工人生产率的提高,这本质上意味着我们做得如何。 换句话说,你的国家在时间和劳动力方面的效率如何? 劳动生产率
什么决定了工人的生产力? 答案很直观。 劳动生产率的第一个决定因素是人力资本。 人力资本
决定劳动生产率的第二个因素是技术变革。 技术变革 发明 创
决定劳动生产率的第三个因素是规模经济。 回想一下,规模经济是行业因规模而获得的成本优势。 (在成本和行业结构中阅读有关规模经济的更多信息。) 再考虑一下虚构的加拿大工人的案例,他可以在一小时内生产 10 条面包。 如果这种生产率的差异仅仅是由于规模经济造成的,那可能是加拿大工人可以使用大型工业规模的烤箱,而美国工人使用的是标准的住宅大小的烤箱。
既然我们已经探索了工人生产率的决定因素,那么让我们来看看经济学家如何衡量经济增长和生产率。
经济增长来源:总生产功能
要分析经济增长的来源,可以考虑生产函数 总生产函数
聚合生产函数的组件
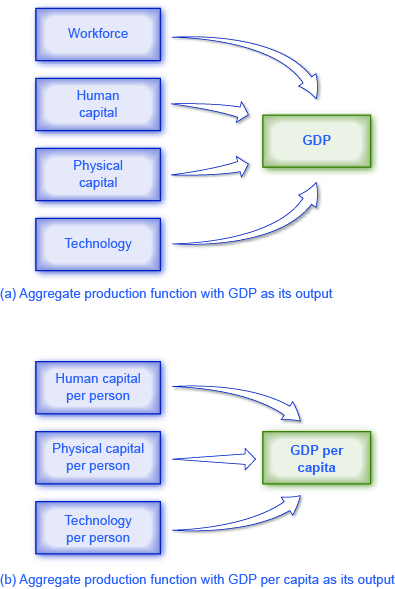
经济学家根据研究重点构建不同的生产功能。 图 1 显示了两个聚合生产函数的示例。 在图 1 (a) 所示的第一个生产函数中,输出为 GDP。 本示例中的输入是劳动力、人力资本、实物资本和技术。 我们将在 “经济增长的组成部分” 模块中进一步讨论这些投入。
聚合生产函数
图 1:总生产函数显示了为整体经济生产产出的内容。 (a) 该总生产功能以国内生产总值作为其产出。 (b) 该总生产函数以人均国内生产总值作为其产出。 由于它是按人均计算的,因此劳动力投入已经计入其他因素,无需单独列出。 衡量生产力
一个经济体的生产率增长率与其人均GDP的增长率密切相关,尽管两者并不相同。 例如,如果在经济体中拥有工作的人口百分比增加,人均国内生产总值将增加,但个体工人的生产率可能不会受到影响。 从长远来看,人均GDP持续增长的唯一途径是普通工人的生产率提高或者资本有互补增长。
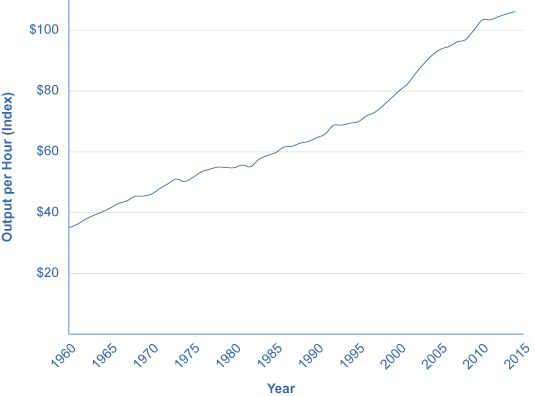
衡量美国每名员工生产率的一个常用标准是员工为雇主的产出贡献的每小时美元价值。 这项措施不包括政府工作人员,因为他们的产出不在市场上出售,因此他们的生产率难以衡量。 它还不包括农业,农业在美国经济中仅占相对较小的份额。 图 2 显示了每小时产出指数,以 2009 年为基准年(当该指数等于 100 时)。 该指数在2014年约等于106。 1972年,该指数等于50,这表明自那时以来,工人的生产率翻了一番多。
1947—2011 年美国经济中每小时工作的产出
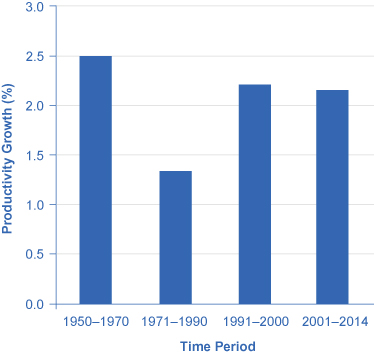
图 2:每小时工作产出是衡量员工生产率的指标。 在美国经济中,与1970年代和1980年代相比,1960年代和1990年代中期的工人生产率增长得更快。 但是,这些增长率差异每年只有几个百分点。 仔细观察,在直线不断变化的斜率中看到它们。 2014年,美国工人的平均每小时产量是1970年代初的两倍多。 (资料来源:美国劳工部、劳工统计局。) 根据劳工部的数据,美国的生产率增长在1950年代相当强劲,但随后在1970年代和1980年代有所下降,然后在1990年代下半叶和2000年代上半叶再次上升。 事实上,以每小时工作产出变化衡量的生产率从1950年到1970年平均每年3.2%;从1970年到1990年下降到每年1.9%;然后从1991年到现在回升至2.3%以上,2001年之后又略有放缓。 图3显示了自1950年以来在一段时间内的平均年生产率增长率。
1950 年以来的生产率增长
图 3:1950 年至 1970 年间,美国工人生产率的增长非常快。 然后,它在1970年代和1980年代降至较低水平。 20世纪90年代末和21世纪初,生产率有所回升,但随后生产率在2000年代略有下降。 有人认为,20世纪90年代末和21世纪初的生产率反弹标志着建立在更高生产率增长基础上的 “新经济” 的开始,但这要等到更长的时间过去后才能确定。 (资料来源:美国劳工部、劳工统计局。) “新经济” 之争
近年来,经济学家之间就20世纪90年代下半叶美国生产率的复苏正在形成争议。 一种思想流派认为,美国在1990年代通信和信息技术的非凡进步的基础上发展了一种 “新经济”。 最乐观的支持者认为,它将在未来几十年内带来更高的平均生产率增长。 另一方面,悲观主义者认为,即使是五到十年的强劲生产率增长也不能证明更高的生产率会持续很长时间。 很难推断出2000年代后期的长期生产率趋势,因为2008-2009年的严重衰退以及产出和就业的急剧但并非完全同步的下降,使任何解释都变得复杂。 尽管2009年和2010年的生产率增长很高(约3%),但此后有所放缓。
生产率的增长
注:比较两个国家的经济
经济合作与发展组织(经合组织)追踪每小时实际GDP的年增长率数据。 你可以在经合组织数据网页 “整体经济中的劳动生产率增长” 上找到这些数据。
第 1 步。 访问上面给出的经合组织网站,选择两个国家进行比较。
第 2 步。 在 “变量” 下拉菜单上,选择 “实际国内生产总值,年增长百分比”,然后记录您最近五年选择的国家/地区的数据。
第 3 步。 返回下拉菜单并选择 “每小时工作的实际国内生产总值,年增长率,百分比”,然后选择您选择 GDP 数据的相同年份的数据。
第 4 步。 比较两个国家的实际国内生产总值增长。 表1提供了澳大利亚和比利时之间的比较示例。
澳大利亚 2009 2010 2011 2012 2013
实际国内生产总值增长 (%)
0.1%
1.0%
2.2%
0.8
0.7%
实际国内生产总值增长/工作时数 (%)
1.9%
— 0.3%
2.4%
3.3%
1.4%
比利时 2009 2010 2011 2012 2013
实际国内生产总值增长 (%)
—3.4
1.6
0.8
—0.6
—0.2
实际国内生产总值增长/工作时数 (%)
—1.3
—1.4
—0.5
—0.3
0.3
表 1
第 5 步。 考虑一下会影响增长的许多因素。 例如,可能影响澳大利亚的一个因素是它与欧洲隔绝,这可能使该国免受全球衰退的影响。 就比利时而言,尽管生产率似乎正在复苏,但全球经济衰退似乎对2009年至2013年间每工作小时的GDP和实际GDP都产生了影响。
持续经济增长的力量
对人们的生活水平而言,没有什么比持续的经济增长更重要的了。 即使增长率的微小变化,如果持续并长期复合,也会对生活水平产生巨大影响。 以表 1 为例,表中的各行显示了几种不同的人均国内生产总值增长率,各列显示了不同的时间段。 简单地假设一个经济体起初的人均国内生产总值为100。 然后,该表使用以下公式来计算未来在给定增长率下的国内生产总值:
\[GDP\,at\,starting\,date\,\times\,(1+growth\,rate\,of\,GDP)^{years}\,=\,GDP\,at\,end\,date\]
例如,一个起初国内生产总值为100并以每年3%的速度增长的经济体将在25年后达到209的国内生产总值;也就是说,100 (1.03) 25 = 209。
表中人均GDP增长最慢的年增长率仅为1%,与美国在生产率增长最疲软的年份所经历的相似。 第二高的年增长率为3%,接近美国经济在20世纪90年代末和2000年代强劲经济期间所经历的水平。 更高的人均增长率,例如每年5%或8%,代表了日本、韩国和中国等经济体的快速增长。
表2显示,即使是经济增长率的几个百分点的差异,如果持续下去,并且随着时间的推移而复杂,也会产生深远的影响。 例如,一个经济体在50年内以1%的年增长率增长,其人均GDP将总共增长64%,在本例中从100增加到164。 但是,一个以5%的年增长率增长的国家在短短10年内将实现(几乎)相同的增长量——从100增长到163年。 经济的快速增长可以带来深刻的转变。 (请参阅以下关于复合增长率与复合利率之间关系的 Clear It Up 专题报道。) 如果增长率为8%,那么从20岁开始的年轻人到30岁时,他们国家的平均生活水平将增加一倍以上,到45岁时将增长近七倍。
增长率 10 年内原件 100 的价值 25 年内原始 100 的价值 50 年内原件 100 的价值
1%
110
128
164
3%
134
209
438
5%
163
338
1,147
8%
216
685
4,690
表2:不同时间段的国内生产总值增长
注意:复合增长率和复合利率有何关系?
如图 2 所示,不同时期 GDP 增长率的公式与《稀缺世界中的选择》中给定数额的金融储蓄如何随着时间的推移以一定的利率增长的公式完全相同。 两种配方都有相同的成分:
原始起始金额,一种是GDP,另一种是财务储蓄金额;
随着时间的推移增加百分比,一种是国内生产总值的增长率,另一种是利率;
以及这种效果发生的时间长度。
回想一下,复利是从过去的利息中赚取的利息。 随着时间的推移,它使财务储蓄总额急剧增长。 同样,复合经济增长率或复合增长率 意味着增长率乘以包括过去GDP增长的基数,随着时间的推移会产生显著影响。
例如,2013年,中央情报局出版的《世界概况》报告称,韩国的国内生产总值为1.67万亿美元,增长率为2.8%。 我们可以估计,按照这种增长率,韩国的GDP将在五年内达到1.92万亿美元。 如果我们将增长率应用于未来五年的年终GDP,我们将计算出在第一年年底,GDP为1.72万亿美元。 在第二年,我们从年终价值1.67美元开始,然后将其增加2%。 第三年从第二年年末的GDP开始,我们将其增长了2%,依此类推,如表3所示。
年 国内生产总值 增长率 2% 年终金额
1
1.67 万亿美元 ×
(1+0.028)
1.72 万亿美元
2
1.72 万亿美元 ×
(1+0.028)
1.76 万亿美元
3
1.76 万亿美元 ×
(1+0.028)
1.81 万亿美元
4
1.81 万亿美元 ×
(1+0.028)
1.87 万亿美元
5
1.87 万亿美元 ×
(1+0.028)
1.92 万亿美元
表 3
计算增长率的另一种方法是应用以下公式:
\[Future\,Value\,=\,Present\,Value\,\times\,(1+g)^n\]
其中 “未来价值” 是五年后的GDP价值,“现值” 是1.64万亿美元的起始GDP金额,“g” 是2%的增长率,“n” 是我们计算增长的周期数。
\[Future\,Value\,=1.67\,\times(1+0.028)^5=\,\$1.92\,trillion\]
关键概念和摘要
生产率,即每名工人或每小时工作所产生的价值,可以用每名工人的GDP水平或每小时的GDP来衡量。 1973年至1989年间,美国经历了生产率放缓。 从那时起,美国的生产率有所回升(尽管当前存在全球衰退)。 目前尚不清楚当前的生产率增长能否持续下去。 生产率增长率是决定一个经济体长期经济增长率和更高工资的主要决定因素。 几十年来,几代人以来,年经济增长率之间看似微小的几个百分点的差异使人均GDP发生了巨大变化。 总生产函数指定了经济中的某些投入,如人力资本、实物资本和技术,如何产生以人均国内生产总值衡量的产出。
复利率和复合增长率的行为方式与生产率相同。 看似微小的百分点变化会随着时间的推移对收入产生重大影响。
关键概念和摘要
生产率,即每名工人或每小时工作所产生的价值,可以用每名工人的GDP水平或每小时的GDP来衡量。 1973年至1989年间,美国经历了生产率放缓。 从那时起,美国的生产率有所回升(尽管当前存在全球衰退)。 目前尚不清楚当前的生产率增长能否持续下去。 生产率增长率是决定一个经济体长期经济增长率和更高工资的主要决定因素。 几十年来,几代人以来,年经济增长率之间看似微小的几个百分点的差异使人均GDP发生了巨大变化。 总生产函数指定了经济中的某些投入,如人力资本、实物资本和技术,如何产生以人均国内生产总值衡量的产出。
复利率和复合增长率的行为方式与生产率相同。 看似微小的百分点变化会随着时间的推移对收入产生重大影响。
词汇表
聚合生产函数
整个经济体将人力资本、有形资本和技术等经济投入转化为以人均国内生产总值计量的产出的过程
复合增长率
增长率乘以包括过去国内生产总值增长的基数
人力资本
工人积累的技能和教育
创新
将知识的进步用于新产品或服务
发明
知识的进步
劳动生产率
每位工人或每小时工作所产生的价值(有时称为工人生产率)
生产功能
企业将劳动力、机械和原材料等经济投入转化为消费者使用的商品和服务等产出的过程
技术变革
发明——知识进步——和创新的结合