24.3: 广义相对论的检验

Last updated
Save as PDF

Page ID: 203123

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

描述水星绕太阳的异常运动，并解释广义相对论如何解释观测到的行为
举例说明光线被大型物体弯曲的证据，正如广义相对论关于时空扭曲的理论所预测的那样

爱因斯坦提出的无非是我们对空间和时间的理解的一次重大革命。这是一种新的重力理论，在这种理论中，质量决定时空的曲率，而曲率反过来控制物体的移动方式。与科学领域的所有新思想一样，无论谁在推动它们，爱因斯坦的理论都必须通过将其预测与实验证据进行比较来检验。这是一个很大的挑战，因为新理论的影响只有在质量相当大的时候才显而易见。（对于较小的质量，它需要测量技术，而这些技术要等到几十年后才可用。）

当扭曲质量很小时，广义相对论的预测必须与牛顿万有引力定律得出的预测一致，毕竟，牛顿万有引力定律在我们的技术和引导太空探测器前往其他行星方面为我们提供了令人钦佩的服务。因此，在熟悉的领域，两种模型的预测之间的差异是微妙的，难以察觉。尽管如此，爱因斯坦还是能够证明其理论的一个证据，该证据可以在现有数据中找到，并提出另一个将在几年后进行检验的证据。

《水星运动》

在我们太阳系中的行星中，水星的轨道离太阳最近，因此受太阳质量产生的时空失真影响最大。爱因斯坦想知道这种失真是否会在水星运动中产生牛顿定律无法预测的明显差异。事实证明，差异很微妙，但确实存在。最重要的是，它已经被测量过了。

水星的轨道高度椭圆，因此它在近日点与太阳的距离只有三分之二左右（这些术语在关于轨道和重力的章节中定义）。 其他行星对水星的引力效应（扰动）使水星的近日点向前推进了可以计算出来。这意味着，从太阳看，每个连续的近日点朝着略有不同的方向出现（图\(\PageIndex{1}\)）。

图\(\PageIndex{1}\) Mercury 的 Wobble。由于各种干扰，诸如水星之类的行星轨道的主轴在太空中稍微旋转。就水星而言，旋转量（或轨道进动）比其他行星施加的引力所能解释的要大一些；广义相对论正好解释了这种差异。水星是离太阳最近的行星，其轨道受太阳附近时空扭曲的影响最大。在这张图中，从一个轨道到另一个轨道的变化被大大夸大了。

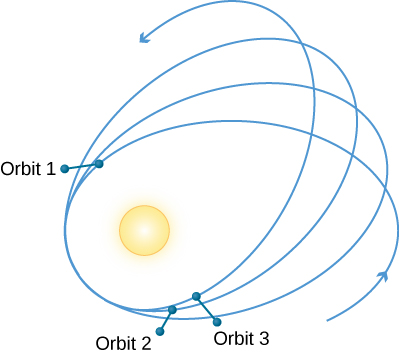
根据牛顿引力，行星施加的引力将使水星的近日点每世纪向前推进约531秒的弧线（弧秒）。但是，在十九世纪，据观察，实际进度为每世纪574弧秒。海王星的共同发现者 Urbain Le Verrier 于 1859 年首次指出了这种差异。正如天王星运动的差异使天文学家得以发现海王星的存在一样，人们认为水星运动的差异可能意味着存在一个未被发现的内部行星。天文学家在太阳附近搜寻这颗行星，甚至以罗马火神的名字命名：火神。（这个名字稍后将在一部关于未来太空旅行的热门电视节目中用于一个著名角色的家乡星球。）

但是从来没有发现过比水星更接近太阳的行星，在爱因斯坦进行计算时，这种差异仍然困扰着天文学家。但是，广义相对论预测，由于太阳周围时空的曲率，水星近日点的推进速度应略高于牛顿引力的预测。结果是使水星轨道的主轴在太空中缓慢旋转，仅因为太阳的重力。广义相对论的预测是，近日点的方向每世纪应再变化 43 弧秒。这与观察到的差异非常接近，这给了爱因斯坦在推进理论时很大的信心。后来，在几颗靠近太阳的小行星的轨道上也观察到了近日点的相对论进展。

星光偏转

爱因斯坦的第二次测试是以前从未观察过的，因此可以很好地证实他的理论。由于在引力场较强的区域，时空更加弯曲，因此我们预计非常靠近太阳的光线似乎会沿着弯曲的路径行驶（图\(\PageIndex{2}\)），就像我们类比中的蚂蚁一样。爱因斯坦根据广义相对论计算出，刚刚掠过太阳表面的星光应该偏转1.75弧秒的角度。能否观察到这样的偏转？

alt — 图靠近太阳的光路\(\PageIndex{2}\)曲率。靠近太阳的星光会因时空的 “扭曲” 而稍微偏转。（这种星光的偏转是称为引力透镜的现象的一个小例子，我们将在《星系的演变与分布》中更详细地讨论这种现象。）在经过太阳之前，来自恒星的光线平行于人物的底部边缘。当它靠近太阳时，路径略有改变。当我们看到光时，我们假设光束在整个旅程中一直沿着直线移动，因此我们测量恒星的位置与其真实位置略有不同。如果我们要在另一个时间观察恒星，当太阳不在路上时，我们将测量它的真实位置。

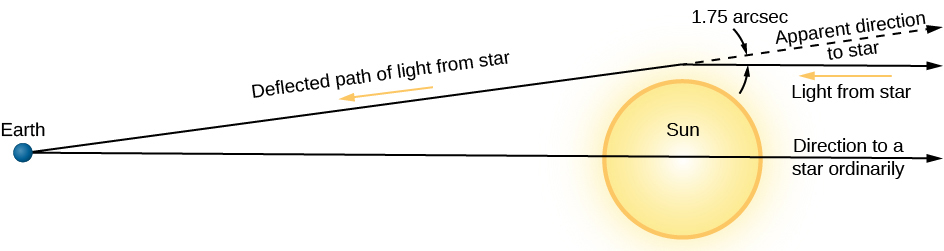
当我们尝试拍摄离太阳很近的星光时，我们遇到了一个小的 “技术问题”：太阳本身就是一种极其明亮的星光来源。但是在日全食期间，太阳的大部分光线都被遮住了，从而可以拍摄太阳附近的恒星。在第一次世界大战期间发表的一篇论文中，爱因斯坦（在德国杂志上写道）提出，日食期间的摄影观测可以揭示太阳附近光线的偏转。

该技术包括在日食前六个月拍摄恒星的照片，并准确测量所有恒星的位置。然后在日食期间拍摄同样的星星。在这个时候，星光必须绕过太阳，穿越明显扭曲的时空，向我们传播。从地球上看，离太阳最近的恒星似乎 “不合时宜” ——稍微偏离太阳不在附近时测得的常规位置。

英国天文学家亚瑟·爱丁顿收到了这篇论文的一份副本通过中立的荷兰，他指出，下一次合适的日食发生在1919年5月29日。英国人组织了两次探险队来观察：一次在西非沿海的普林西比岛上，另一次在巴西北部的索布拉尔。尽管天气存在一些问题，但两次探险都获得了成功的照片。在太阳附近看到的恒星确实是位移的，就测量精度（约为20％）而言，这些变化与广义相对论的预测一致。更现代的无线电波靠近太阳传播的实验证实，实际位移在广义相对论预测的1％以内。

1919年的日食探险队证实了这一理论，这是一次胜利，使爱因斯坦成为了世界名人。

摘要

在弱引力场中，广义相对论的预测与牛顿引力定律的预测一致。但是，在太阳引力更强的情况下，广义相对论做出的预测与牛顿物理学不同，是可以检验的。例如，广义相对论预测，光或无线电波在靠近太阳时会发生偏转，即使太阳系中没有其他行星可以扰乱其轨道，水星在近日点的位置也会每世纪变化43弧秒。这些预测已通过观察得到证实。