24.2: 时空和重力

Last updated
Save as PDF

Page ID: 203139

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

将爱因斯坦对重力的看法描述为在存在大型物体的情况下时空的扭曲
明白，牛顿关于两个大型物体之间引力的概念和爱因斯坦关于时空扭曲的概念是对一个大型物体在存在另一个大型物体的情况下观测到的相同加速度的不同解释

光真的会被地球的质量从直线路径弯曲吗？没有质量的光怎么会受到重力的影响？爱因斯坦更倾向于认为受大质量存在影响的是空间和时间；光束和其他穿越时空的东西，然后发现它们的路径受到影响。光线总是沿着最短的路径行驶，但这条路径可能并不总是直的。这个想法也适用于人类在地球曲面上旅行。假设你想从芝加哥飞往罗马。由于飞机无法穿过地球的固体，因此最短的距离不是直线，而是大圆的弧线。

联系：质量、空间和时间

为了展示爱因斯坦的洞察力的真正含义，让我们首先考虑一下我们如何在时空中定位事件。例如，假设你必须向担心的学校官员描述一下你的室友尝试在壁炉里煮烤肉串时你的房间里发生的火灾。你解释说你的宿舍位于 College Avenue 6400 号，这条街在你的城镇地图上向左向右延伸；你在五楼，它告诉你在上下方向的位置；而你是从电梯回来的第六个房间，它告诉你在向前向后的方向所处的位置。然后你解释说火灾是在下午 6:23 爆发的（但很快得到控制），这说明了事件的发生时间。宇宙中的@@ 任何事件，无论是近处还是远处，都可以使用空间的三维和一维时间来精确定位。

牛顿认为时空是完全独立的，直到二十世纪初，这种观点一直是公认的观点。但是爱因斯坦表明，时空之间存在着密切的联系，只有将两者结合起来（我们称之为时空），我们才能正确地描绘物理世界。在下一小节中，我们将更仔细地研究时空。

爱因斯坦一般理论的要点是，物质的存在会曲线或扭曲时空结构。这种时空曲线用重力来标识。当其他东西 —— 光束、电子或星际飞船 E nterpri se —— 进入这样一个时空失真的区域时，它的路径将与没有物质时的路径不同。正如美国物理学家约翰·惠勒总结的那样：“物质告诉时空如何弯曲；时空告诉物质如何移动。”

时空中的失真量取决于所涉及材料的质量以及其浓度和紧凑程度。陆地物体，比如你正在阅读的书，质量太小，不会产生任何明显的失真。牛顿的重力视角非常适合建造桥梁、摩天大楼或游乐园游乐设施。但是，广义相对论确实有一些实际应用。由于考虑了广义相对论和狭义相对论对环绕地球轨道的GPS卫星的影响，每部智能手机中的GPS（全球定位系统）都能告诉你在5到10米范围内的位置。

与书本或你的室友不同，星星在时空中会产生可测量的扭曲。与具有相同质量的红巨人相比，具有更强的表面重力的白矮星在其表面上方产生的变形更大。所以，你看，我们最终会再次讨论恒星的崩溃，但在更详细地讨论爱因斯坦的想法（以及它们的证据）之前不会讨论这个话题。

时空示例

我们怎样才能理解一些（大量）质量的存在会导致时空失真？让我们试试下面的比喻。你可能已经看过纽约市的地图，这些地图将这座高耸的大都市的全部三个维度挤在一张纸上，但仍然有足够的信息，这样游客就不会迷路。让我们用时空图做类似的事情。

例如\(\PageIndex{1}\)，该图显示了一名驾车者在堪萨斯州的一段路段上向东行驶的进度，那里的乡村绝对平坦。由于我们的驾驶者只能沿东西向方向行驶，并且地形平坦，因此我们可以忽略其他两个维度的空间。他离开家后经过的时间显示在 y 轴上，向东行驶的距离显示在 x 轴上。从 A 到 B 他以统一的速度开车；不幸的是，统一的速度太快了，一辆警车发现了他。从 B 到 C 他停下来领取门票，在太空中没有取得任何进展，只能穿越时空。从 C 到 D 他开得更慢，因为警车在他身后。

alt — 图\(\PageIndex{1}\)时空图。这张图显示了驾车者在堪萨斯州平坦景观中向东行驶的进度。沿水平轴绘制行进距离。自驾驶者离开起点以来经过的时间沿垂直轴绘制。

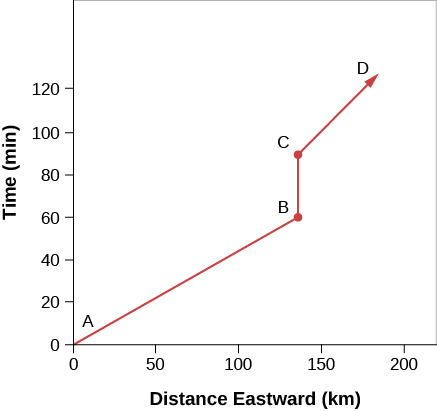
现在让我们试着用二维来说明时空的扭曲。在这种情况下，我们将（根据我们的想象）使用橡胶板，如果我们在上面放置物体，该橡胶板会拉伸或变形。

让我们想象一下在四个柱子上拉紧我们的橡胶板。为了完成这个比喻，我们需要一些通常沿直线传播的东西（就像光一样）。假设我们有一只非常聪明的蚂蚁 —— 也许是漫画超级英雄 Ant-Man 的朋友 —— 它已经受过直线行走的训练。

我们从橡胶板和蚂蚁开始，模拟没有质量的空白空间。我们把蚂蚁放在床单的一侧，它沿着一条漂亮的直线走到另一边（图\(\PageIndex{2}\)）。接下来，我们在橡胶板上放一小粒沙子。沙子确实会稍微扭曲纸张，但这不是我们或蚂蚁可以测量的失真。如果我们派遣蚂蚁让它靠近沙粒，但不在沙粒之上，那么继续直线行走就没什么麻烦了。

现在我们抓住质量多一点的东西——比如说一块小卵石。它会使纸张稍微弯曲或扭曲其位置。如果我们把蚂蚁送到这个区域，它会发现它的路径因纸张的变形而略有改变。失真不大，但是如果我们仔细地沿着蚂蚁的路径行驶，我们会注意到它与直线略有偏离。

随着我们增加放置在纸张上的物体的质量，效果会变得更加明显。假设我们现在使用的是巨大的镇纸。如此重的物体会非常有效地扭曲或扭曲橡胶板，从而在其中造成良好的下垂。从我们的角度来看，我们可以看到镇纸附近的纸张不再是直的。

alt — 图：时空的\(\PageIndex{2}\)三维类比。在平坦的橡胶板上，训练有素的蚂蚁可以毫不费力地直线行走。当一个巨大的物体在纸张上产生一个很大的凹陷时，蚂蚁会发现它的路径发生了巨大变化（扭曲）。

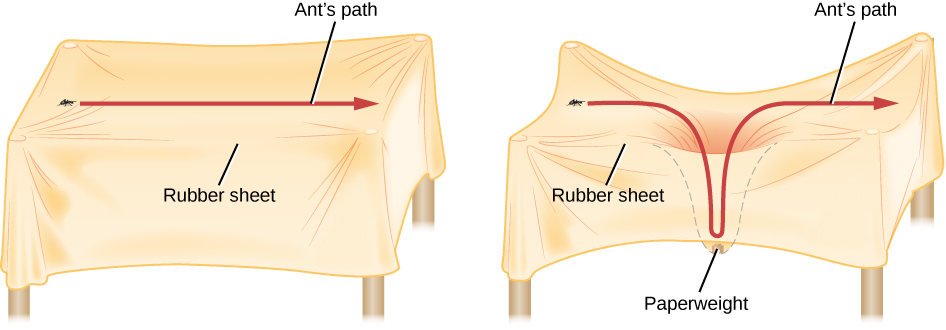
现在，让我们再次派遣蚂蚁踏上一段旅程，让它接近镇纸，但不是在镇纸之上。远离镇纸，蚂蚁可以毫不费力地行走，这对我们来说是直视的。但是，当蚂蚁接近镇纸时，它被迫进入下垂。然后它必须爬上另一边，然后才能恢复在纸张未失真的部分行走。尽管如此，蚂蚁正在沿着最短的路径行驶，但这并不是它自己的错（毕竟，蚂蚁无法飞行，所以它必须留在床单上）这条路径因床单本身的变形而弯曲。

同样，根据爱因斯坦的理论，光总是沿着穿越时空的最短路径行驶。但是与高浓度物质相关的质量会扭曲时空，最短、最直接的路径不再是直线，而是曲线。

在我们测量光路的变化之前，质量必须有多大？ 1916年，当爱因斯坦首次提出他的理论时，地球表面没有发现任何变形（因此，在我们的类比中，地球可能扮演了沙粒的角色）。为了探测爱因斯坦所描述的效果，必须有像太阳这样的质量的东西（我们将在下一节中讨论如何使用太阳测量这种效应）。

我们比喻中的镇纸可能是白矮星或中子星。在这些紧凑的大型物体表面附近，时空的扭曲要比在太阳表面附近更大。而且，回到本章开头描述的情况，当质量超过太阳三倍的恒星核心永远崩溃时，与之非常接近的时空扭曲可能会变得令人难以置信。

摘要

通过考虑等价原理的后果，爱因斯坦得出结论，我们生活在弯曲的时空中。物质的分布决定了时空的曲率；进入时空区域的其他物体（甚至光）必须遵循其曲率。光必须改变其在大型物体附近的路径，不是因为光会被重力弯曲，而是因为时空会弯曲。

词汇表

时空: 由一个时间和三个空间坐标构成的系统，可以据此指定事件的时间和地点