24.1:介绍广义相对论
- Page ID
- 203124
学习目标
在本节结束时,您将能够:
- 讨论广义相对论的一些关键思想
- 认识到一个人的重力和加速度体验是可以互换和无法区分的
- 区分牛顿式的重力观念和爱因斯坦的重力观念
- 认识为什么广义相对论对于理解黑洞的本质是必要的
大多数恒星以白矮星或中子星的形式结束生命。 但是,当一颗非常大的恒星在生命的尽头崩溃时,即使是密集的中子之间的相互排斥也无法支撑核心抵御自身的重量。 如果恒星核心的剩余质量是太阳的三倍以上 (\(M_{\text{Sun}}\)),我们的理论预测没有任何已知的力量可以阻止它永远崩溃! 重力只会压倒所有其他力量并压碎核心,直到它占据无限小的体积。 发生这种情况的恒星可能会成为理论上预测的最奇怪的物体之一——黑洞。
要理解黑洞是什么样子以及它如何影响周围环境,我们需要一种能够描述重力在如此极端情况下作用的理论。 迄今为止,我们最好的引力理论是阿尔伯特·爱因斯坦在1916年提出的广义相对论。
广义相对论是二十世纪主要的智力成就之一;如果是音乐,我们可以将其与贝多芬或马勒的伟大交响曲进行比较。 但是,直到最近,科学家们几乎不需要更好的引力理论;艾萨克·牛顿的万有引力定律(参见 Orbits and Gravity)的想法完全足以满足我们在日常生活中处理的大多数物体。 但是,在过去的半个世纪中,广义相对论已不仅仅是一个好主意;现在,它对于理解脉冲星、类星体(将在活跃星系、类星体和超大质量黑洞中讨论)以及许多其他天体和事件(包括我们的黑洞)至关重要我将在这里讨论。
我们也许应该提一下,在天文学课程中,许多学生开始感到有点紧张(也许希望他们上过植物学或其他地球课程来满足科学要求)。 这是因为在流行文化中,爱因斯坦已成为数学辉煌的象征,这是大多数人无法企及的(图\(\PageIndex{1}\))。

因此,当我们写下广义相对论是爱因斯坦的作品时,你可能有点担心,坚信爱因斯坦所做的任何事情都一定超出了你的理解。 这种流行的观点既不幸又错误。 尽管广义相对论的详细计算确实涉及大量的高等数学,但基本思想并不难理解(事实上,它们为我们提供了一个新的世界视角几乎是诗意的)。 此外,广义相对论超越了牛顿著名的 “反方引力” 定律;它有助于解释物质如何在时空中与其他物质相互作用。 这种解释力是任何成功的科学理论都必须满足的要求之一。
等价原理
导致广义相对论形成的基本见解始于一个非常简单的想法:如果你能够跳下高楼自由坠落,你就不会感觉到自己的重量。 在本章中,我们将描述爱因斯坦如何以这个想法为基础,就时空本身的结构得出全面的结论。 他称之为 “我一生中最幸福的想法”。
爱因斯坦本人举了一个日常例子来说明这种效果(图\(\PageIndex{2}\))。 请注意,当高速电梯从停靠点加速到快速下降时,你的体重似乎是如何减轻的。 同样,在开始快速向上移动的电梯中,你的体重似乎会增加。 这种效果不仅仅是你的感觉:如果你站在这样的电梯里的体重秤上,你可以测量自己的体重变化(你实际上可以在一些科学博物馆进行这个实验)。
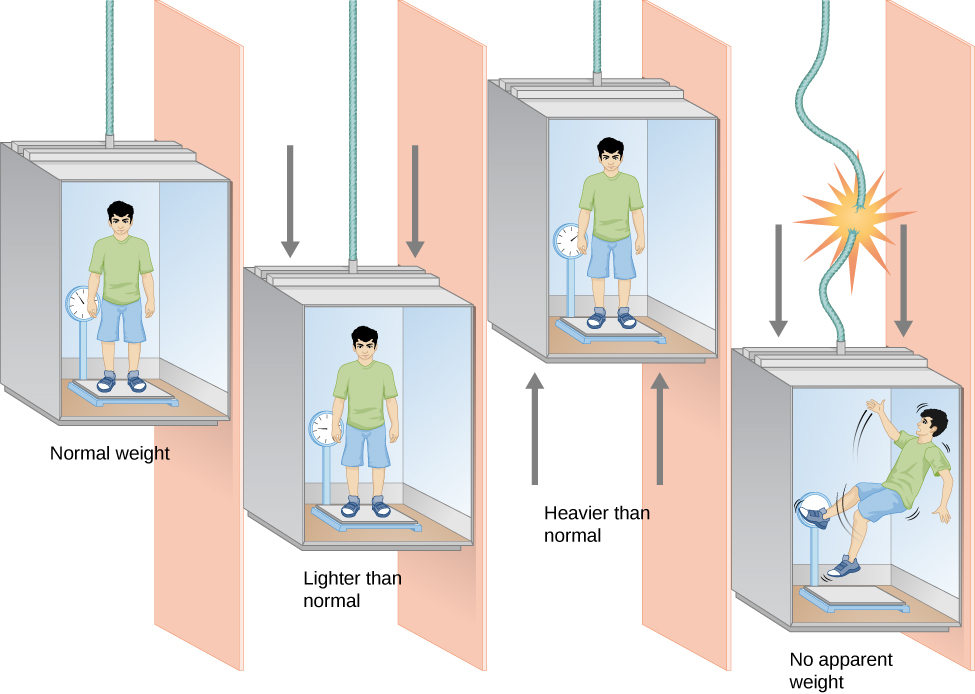
在自由落下的电梯中,没有空气摩擦,你会完全减轻体重。 我们通常不喜欢切断固定电梯的电缆来尝试这个实验,但是通过将飞机带到高空然后快速坠落一会儿,可以实现近乎失重的状态。 美国宇航局就是这样训练宇航员体验太空自由落体的;1995年电影《阿波罗13号》中的失重场景也是以同样的方式拍摄的。 (此后,电影制片人设计了其他方法,使用水下拍摄、线控特技和计算机图形学来营造重力和火星人等电影中出现的失重外观。)
观看 NASA 如何使用 “失重” 环境来帮助训练宇航员。
表达爱因斯坦想法的另一种方式是:假设我们有一艘太空飞船,里面有一个没有窗户的实验室,配备了进行科学实验所需的所有工具。 现在,想象一下,一位天文学家在庆祝科学突破的漫长夜后醒来,发现自己被封锁在这个实验室里。 她不知道怎么回事,但注意到自己体重不足。 这可能是因为她和实验室远离任何重力源,要么处于静止状态,要么以稳定的速度在太空中移动(在这种情况下,她有足够的时间醒来)。 但这也可能是因为她和实验室正在自由落向像地球这样的行星(在这种情况下,她可能要先检查一下自己与地表的距离,然后再煮咖啡)。
爱因斯坦的假设是,她无法在封闭的实验室内进行任何实验来确定她是在太空中漂浮还是在引力场中自由坠落。 1 就她而言,这两种情况是完全相同的。 这种认为自由落体与零重力没有区别,因此等同于零重力的想法被称为等效原理。
重力还是加速度?
爱因斯坦的简单想法有很大的影响。 让我们先考虑一下,如果两个笨拙的人从对面的河岸跳入无底洞会发生什么(图\(\PageIndex{3}\))。 如果我们忽略空气摩擦,那么我们可以说,当它们自由落下时,它们都以相同的速度向下加速,并且感觉不到外力作用在它们身上。 他们可以来回投球,总是将球直接对准对方,就好像没有重力一样。 球的落球速度与他们相同,因此球始终保持在它们之间的直线上。
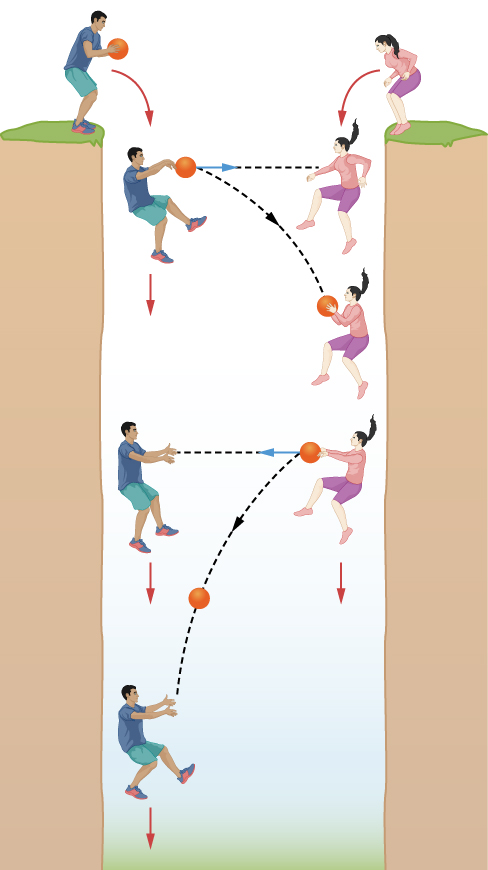
这样的捕捉游戏在地球表面有很大的不同。 每个长大后感觉到重力的人都知道,一个球一旦被抛出,就会掉到地上。 因此,为了与某人进行接球,你必须将球向上瞄准,这样球才能跟随弧线 —— 在向前移动时上升然后下降 —— 直到球在另一端被抓住。
现在假设我们将坠落的人和球隔离在一个与他们一起掉落的大盒子里。 盒子里没有人知道任何引力。 如果他们放开球,球不会落到盒子的底部或其他任何地方,而只是停留在那里或沿直线移动,这取决于球是否被赋予任何动作。
环绕地球运行的国际空间站(ISS)中的宇航员生活在与封闭在自由落体箱中的人的环境一样(图\(\PageIndex{4}\))。 在轨道运行的国际空间站实际上是在环绕地球 “自由坠落”。 在自由落体时,宇航员生活在一个陌生的世界里,那里似乎没有引力。 人们可以推一下扳手,然后它会以恒定的速度在轨道实验室中移动。 空中的一支铅笔还留在那里,好像没有力量在上面起作用一样。

在国际空间站的 “失重” 环境中,移动几乎不需要付出任何努力。 观看宇航员凯伦·尼伯格(Karen Nyberg)演示如何用一根人发的力量推动自己。
但是,外表具有误导性。 在这种情况下有一股力量。 在地球重力的推动下,国际空间站和宇航员都在地球周围不断坠落。 但是,既然所有引力——航天飞机、宇航员、扳手和铅笔——都集中在国际空间站内,所有引力似乎都不存在。
因此,在轨道运行的国际空间站为等效原理提供了一个很好的例子,即如何通过正确的加速度完全补偿重力的局部影响。 对宇航员来说,在地球上坠落产生的效果与远离太空产生的效果相同,远离所有引力影响。
光与物质之路
爱因斯坦假设等价原理是自然界的基本事实,任何航天器内部都没有任何实验可以让宇航员区分在偏远空间失重和在像地球这样的行星附近自由落体。 这也适用于用光束进行的实验。 但是,当我们在实验中使用光的那一刻,我们得出了一些非常令人不安的结论——正是这些结论使我们得出了广义相对论和新的引力观。
从日常观察来看,在我们看来,很明显,光束是直线传播的。 想象一下,一艘太空飞船正在远离任何重力的空旷空间中移动。 将激光束从船的后部发送到前方,它会沿着一条漂亮的直线移动,并降落在与它离开后墙的正对面的前墙上。 如果等价原理真的普遍适用,那么在地球上自由落体时进行的同样的实验应该会给我们同样的结果。
现在想象一下,宇航员再次沿着飞船的长度照射一束光束。 但是,如图所示\(\PageIndex{5}\),这次轨道空间站在光线离开后墙和撞到前墙之间稍微落下。 (图中严重夸大了跌幅\(\PageIndex{5}\)以说明其影响。) 因此,如果光束沿直线行驶,但飞船的路径向下弯曲,则光线照射前墙的点应高于其离开点的位置。
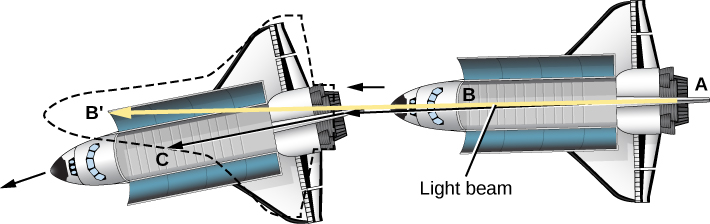
但是,这将违反等效原则——这两个实验会得出不同的结果。 因此,我们面临着放弃两个假设之一的问题。 要么等价原理不正确,要么光并不总是直线传播。 爱因斯坦没有放弃当时看似荒谬的想法,而是想出了如果光有时不走直线会发生什么。
让我们假设等价原理是正确的。 然后,光束必须直接到达它在船上起始点的对面。 光线,就像来回投掷的球一样,必须随飞船在环绕地球的轨道上落下(见图\(\PageIndex{5}\))。 这会使它的路径向下弯曲,就像球的路径一样,因此光线会击中与球的起点正对面的前墙。
仔细想想,你很可能会得出结论,这似乎不是什么大问题:为什么光线不能像球一样落下? 但是,正如《辐射与光谱》中所讨论的那样,光与球截然不同。 球有质量,而光没有。
这就是爱因斯坦的直觉和天才使他得以实现深刻飞跃的地方。 他给我们思维实验的奇怪结果赋予了物理意义。 爱因斯坦建议光线向下弯曲以迎接航天飞机的正面,因为地球的重力实际上会弯曲时空结构。 我们接下来将解释这个激进的想法,它使光在空旷空间和自由落体中的行为保持不变,但它改变了我们对空间和时间的一些最基本和最珍贵的观念。 我们认真对待爱因斯坦的建议的原因是,正如我们将看到的那样,现在的实验清楚地表明他的直觉飞跃是正确的。
关键概念和摘要
爱因斯坦提出了等价原理作为广义相对论的基础。 根据这一原理,任何人或任何在封闭环境中进行的实验都无法区分自由落体和没有重力。
脚注
1 严格来说,只有在实验室非常小的情况下才是这样。 在真实实验室中,由于重力而自由坠落的不同位置不可能都与负责产生引力的物体保持相同的距离。 在这种情况下,位于不同位置的物体将经历略有不同的加速度。 但这一点并不能使爱因斯坦从这种思路中得出的等价原则失效。
词汇表
- 等价原理
- 概念,即在足够局部化的环境中,引力和合适的加速度是无法区分的
- 广义相对论
- 爱因斯坦关于重力与时空结构(几何)的理论


