9.1：简化和使用平方根

Last updated
Save as PDF

Page ID: 204446

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

使用平方根简化表达式
估算平方根
近似平方根
使用平方根简化变量表达式

做好准备

在开始之前，请参加这个准备测验。

简化：ⓐ$9^2$ ⓑ$(−9)^2$ ⓒ$−9^2$。
如果你错过了这个问题，请查看 [链接]。
将 3.846 四舍五入到最接近的百分之一。
如果你错过了这个问题，请查看 [链接]。
对于每个数字，确定它是实数还是不是实数：
ⓐ$−\sqrt{100}$ ⓑ$\sqrt{−100}$。
如果你错过了这个问题，请查看 [链接]。

使用平方根简化表达式

请记住，当一个数字 n 乘以自身时，我们会将其写入$n^2$和读取 “n 平方”。例如，$15^2$读数为 “15 平方”，225 被称为 15 的平方，因为$15^2=225$。

定义：数字的平方

if$n^2=m$，那么 m 是 n 的平方。

有时我们需要反向看数字和它们的平方之间的关系。因为 225 是 15 的平方，我们也可以说 15 是 225 的平方根。平方为 m 的数字称为 m 的平方根。

定义：一个数字的平方根

if$n^2=m$，那么 n 是 m 的平方根。

通知$(−15)^2=225$ also, so −15 is also a square root of 225. Therefore, both 15 and −15 are square roots of 225.

因此，每个正数都有两个平方根——一个正数和一个负数。如果我们只想要一个正数的正平方根呢？ 激进符号$\sqrt{m}$，表示正平方根。正平方根也称为主平方根。

我们还使用激进符号来表示零的平方根。因为$0^2=0$，$\sqrt{0}=0$。请注意，零只有一个平方根。

定义：平方根表示法

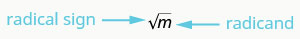
$这个数字是平方根符号内的 m 的图片。该符号被标记为激进符号，m 被标记为 radicand。$

$\sqrt{m}$被读作 “m 的平方根”。

如果$m=n^2$，那么$\sqrt{m}=n$，对于$n \ge 0$。

m 的平方根是正数$\sqrt{m}$，其平方为 m。

由@@ 于 15 是 225 的正平方根，所以我们写$\sqrt{225}=15$. Fill in 图是为了制作一个平方根表，你可以在编写本章时参考。

此表有十五列和两行。第一行包含以下数字：1 的平方根、4 的平方根、9 的平方根、16 的平方根、25 的平方根、36 的平方根、49 的平方根、64 的平方根、81 的平方根、121 的平方根、121 的平方根、平方根144 的平方根，169 的平方根，196 的平方根，225 的平方根。除最后一列外，第二行完全为空。数字 15 在最后一列中。

我们知道每个正数都有两个平方根，激进符号表示正数。我们写$\sqrt{225}=15$。如果我们想找到一个数字的负平方根，我们在激进符号前面放一个负数。例如，$−\sqrt{225}=−15$。

示例$\PageIndex{1}$

简化：

$\sqrt{36}$
$\sqrt{196}$
$−\sqrt{81}$
$−\sqrt{289}$。

回答: 1。
\[\begin{array}{ll} {}&{\sqrt{36}}\\ {\text{Since} 6^2=36}&{6}\\ \end{array}\]
2。
\[\begin{array}{ll} {}&{\sqrt{196}}\\ {\text{Since} 14^2=196}&{14}\\ \end{array}\]
3。
\[\begin{array}{ll} {}&{−\sqrt{81}}\\ {\text{The negative is in front of the radical sign}}&{−9}\\ \end{array}\]
4。
\[\begin{array}{ll} {}&{−\sqrt{289}}\\ {\text{The negative is in front of the radical sign}}&{−17}\\ \end{array}\]

示例$\PageIndex{2}$

简化：

$−\sqrt{49}$
$\sqrt{225}$。

回答

−7
15

示例$\PageIndex{3}$

暗示：

$\sqrt{64}$
$−\sqrt{121}$。

回答

8
−11

示例$\PageIndex{4}$

简化：

$\sqrt{−169}$
$ −\sqrt{64}$

回答

1。

\[\begin{array}{ll} {}&{\sqrt{−169}}\\ {\text{There is no real number whose square is} s−169}&{\sqrt{−169} \text{is not a real number.}}\\ \end{array}\]

2。

\[\begin{array}{ll} {}&{−\sqrt{64}}\\ {\text{The negative is in front of the radical sign}}&{−8}\\ \end{array}\]

示例$\PageIndex{5}$

简化：

$\sqrt{−196}$
$−\sqrt{81}$。

回答

不是实数
−9

示例$\PageIndex{6}$

简化：

$−\sqrt{49}$
$\sqrt{ −121}$。

回答

−7
不是实数

当使用运算顺序来简化具有平方根的表达式时，我们将激进视为分组符号。

示例$\PageIndex{7}$

简化：

$\sqrt{25} +\sqrt{144}$
$\sqrt{25+144}$。

回答: 1。

\[\begin{array}{ll} {}&{\sqrt{25} +\sqrt{144}}\\ {\text{Use the order of operations}}&{5+12}\\ {\text{Simplify.}}&{17}\\ \end{array}\]

2。

\[\begin{array}{ll} {}&{\sqrt{25+144}}\\ {\text{Simplify under the radical sign.}}&{\sqrt{169}}\\ {\text{Simplify.}}&{13}\\ \end{array}\]

请注意第 1 部分和第 2 部分中的不同答案！

示例$\PageIndex{8}$

简化：

$\sqrt{9}+\sqrt{16}$
$\sqrt{9+16}$.

回答

示例$\PageIndex{9}$

简化：

$\sqrt{64+225}$
$\sqrt{64}+\sqrt{225}$。

回答

估算平方根

到目前为止，我们只考虑了完美平方数的平方根。其他数字的平方根不是整数。看下表。

数字	平方根
4	$\sqrt{4}=2$
5	$\sqrt{5}$
6	$\sqrt{6}$
7	$\sqrt{7}$
8	$\sqrt{8}$
9	$\sqrt{9}=3$

4 到 9 之间的数字的平方根必须介于两个连续的整数 2 和 3 之间，并且它们不是整数。根据上表中的模式，我们可以说它$\sqrt{5}$必须介于 2 和 3 之间。使用不等式符号，我们这样写：

$2<\sqrt{5}<3$

示例$\PageIndex{10}$

估计两个连续整数$\sqrt{60}$之间的值。

回答

想想最接近 60 的完美平方数。用这些完美的正方形和它们的正方根做一张小桌子。

$。$
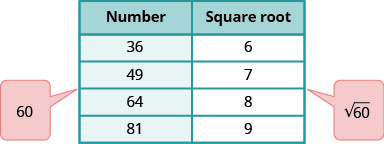
在两个连续的完美正方形之间找到 60。	$。$
$\sqrt{60}$介于它们的平方根之间。	$。$

示例$\PageIndex{11}$

估计两个连续整数$\sqrt{38}$之间的平方根。

回答: $6<\sqrt{38}<7$

示例$\PageIndex{12}$

估计两个连续整数$\sqrt{84}$之间的平方根。

回答: $9<\sqrt{84}<10$

近似平方根

有一些数学方法可以近似平方根，但是现在大多数人使用计算器来找到它们。在计算器上找到$\sqrt{x}$密钥。您将使用此键来估算平方根。

当你使用计算器找出一个不是完美正方形的数字的平方根时，你看到的答案不是确切的平方根。它是一个近似值，精确到计算器显示屏上显示的位数。近似值的符号为$\approx$，读为 “大约”。

假设你的计算器有 10 位数的显示屏。你会明白的

$\sqrt{5} \approx 2.236067978$

如果我们想四舍五入$\sqrt{5}$到小数点后两位，我们会说

$\sqrt{5} \approx 2.24$

我们怎么知道这些值是近似值而不是精确值？看看当我们把它们对齐时会发生什么：

\[\begin{array}{c} {(2.236067978)^2=5.000000002}\\ {(2.24)^2=5.0176}\\ \end{array}\]

它们的平方接近 5，但不完全等于 5。

使用计算器上的平方根键然后四舍五入到小数点后两位，我们可以找到：

\[\begin{array}{c} {\sqrt{4}=2}\\ {\sqrt{5} \approx 2.24}\\ {\sqrt{6} \approx 2.45}\\ {\sqrt{7} \approx 2.65}\\ {\sqrt{8} \approx 2.83}\\ {\sqrt{9}=3}\\ \end{array}\]

示例$\PageIndex{13}$

四舍五$\sqrt{17}$入到小数点后两位。

回答: \[\begin{array}{ll} {}&{\sqrt{17}}\\ {\text{Use the calculator square root key.}}&{4.123105626...}\\ {\text{Round to two decimal places.}}&{4.12}\\ {}&{\sqrt{17} \approx 4.12} \end{array}\]

示例$\PageIndex{14}$

四舍五$\sqrt{11}$入到小数点后两位。

回答: $\approx 3.32$

示例$\PageIndex{15}$

四舍五$\sqrt{13}$入到小数点后两位。

回答: $\approx 3.61$

使用平方根简化变量表达式

如果我们必须用变量找到表达式的平方根怎么办？考虑一下$\sqrt{9x^2}$。你能想到一个正方形的表达式$9x^2$吗？

\[\begin{array}{cc} {(?)^2=9x^2}&{}\\ {(3x)^2=9x^2}&{\text{so} \sqrt{9x^2}=3x}\\ \end{array}\]

当我们使用激进符号取变量表达式的平方根时，我们应该指定 x≥ 0x≥ 0 以确保我们得到主平方根。

但是，在本章中，我们将假设平方根表达式中的每个变量都代表一个非负数，因此我们不会在每个激进$x \ge 0$旁边写字。

那么较高变量幂的平方根呢？想想我们在第 6 章中使用的指数的幂属性。

$(a^m)^n=a^{m·n}$

如果我们进行平方$a^m$，则指数将变成 2m。

$(a^m)^2=a^{2m}$

这如何帮助我们计算平方根？让我们来看几个：

\[\begin{array}{cc} {\sqrt{25u^8}=5u^4}&{\text{Because} (5u^4)^2=25u^8}\\ {\sqrt{16r^{20}}=4r^{10}}&{\text{Because} (4r^{10})^2=16r^{20}}\\ {\sqrt{196q^{36}}=14q^{18}}&{\text{Because} (14r^{18})^2=196q^{36}}\\ \end{array}\]

示例$\PageIndex{16}$

简化：

$\sqrt{x^6}$
$\sqrt{y^{16}}$

回答: 1。

\[\begin{array}{ll} {}&{\sqrt{x^6}}\\ {\text{Since} (x^3)^2=x^6}&{x^3}\\ \end{array}\]

2。

\[\begin{array}{ll} {}&{\sqrt{y^{16}}}\\ {\text{Since} (y^8)^2=y^{16}}&{y^8}\\ \end{array}\]

示例$\PageIndex{17}$

简化：

$\sqrt{y^8}$
$\sqrt{z^{12}}$。

回答

$y^4$
$z^6$

示例$\PageIndex{18}$

简化：

$\sqrt{m^4}$
$\sqrt{b^{10}}$。

回答

$m^2$
$b^5$

示例$\PageIndex{19}$

简化：$\sqrt{16n^2}$

回答: \[\begin{array}{ll} {}&{\sqrt{16n^2}}\\ {\text{Since} (4n)^2=16n^2}&{4n}\\ \end{array}\]

示例$\PageIndex{20}$

简化：$\sqrt{64x^2}$。

回答: $8x$

示例$\PageIndex{21}$

简化：$\sqrt{169y^2}$。

回答: $13y$

示例$\PageIndex{22}$

简化：$−\sqrt{81c^2}$。

回答: \[\begin{array}{ll} {}&{−\sqrt{81c^2}}\\ {\text{Since} (9c)^2=81c^2}&{−9c}\\ \end{array}\]

示例$\PageIndex{23}$

简化：$−\sqrt{121y^2}$。

回答: $−11y$

示例$\PageIndex{24}$

简化：$−\sqrt{100p^2}$。

回答: $−10p$

示例$\PageIndex{25}$

简化：$\sqrt{36x^{2}y^{2}}$。

回答: \[\begin{array}{ll} {}&{\sqrt{36x^{2}y^{2}}}\\ {\text{Since} (6xy)^2=\sqrt{36x^{2}y^{2}}}&{6xy}\\ \end{array}\]

示例$\PageIndex{26}$

简化：$\sqrt{100a^{2}b^{2}}$。

回答: 10ab

示例$\PageIndex{27}$

简化：$\sqrt{225m^{2}n^{2}}$。

回答: 15mn

示例$\PageIndex{28}$

简化：$\sqrt{64p^{64}}$。

回答: \[\begin{array}{ll} {}&{\sqrt{64p^{64}}}\\ {\text{Since} (8p^8)^2=\sqrt{64p^{64}}}&{8p^8}\\ \end{array}\]

示例$\PageIndex{29}$

简化：$\sqrt{49x^{30}}$。

回答: $7x^{15}$

示例$\PageIndex{30}$

简化：$\sqrt{81w^{36}}$

回答: $9w^{18}$

示例$\PageIndex{31}$

简化：$\sqrt{121a^{6}b^{8}}$

回答: \[\begin{array}{ll} {}&{\sqrt{121a^{6}b^{8}}}\\ {\text{Since} (11a^{3}b^{4})^2=\sqrt{121a^{6}b^{8}}}&{11a^{3}b^{4}}\\ \end{array}\]

示例$\PageIndex{32}$

简化：$\sqrt{169x^{10}y^{14}}$

回答: $13x^{5}y^{7}$

示例$\PageIndex{33}$

简化：$\sqrt{144p^{12}q^{20}}$

回答: $\sqrt{12p^{6}q^{10}}$

访问此在线资源，获取更多指导和平方根练习。

平方根

关键概念

请注意，负数的平方根不是实数。
每个正数都有两个平方根，一个正数和一个负数。正数的正平方根是主平方根。
我们可以使用附近的完美平方来估算平方根。
我们可以用计算器来估算平方根。
当我们使用激进符号取变量表达式的平方根时，我们应该指定该符号$x \ge 0$以确保我们得到主平方根。

词汇表

数字的平方

if$n^2=m$，那么 m 是 n 的平方

一个数字的平方根

if$n^2=m$，那么 n 是 m 的平方根

平方根表示法

如果$m=n^2$，那么$\sqrt{m}=n$。我们读$\sqrt{m}$作 “m 的平方根”。

数字	平方根
4	\(\sqrt{4}=2\)
5	\(\sqrt{5}\)
6	\(\sqrt{6}\)
7	\(\sqrt{7}\)
8	\(\sqrt{8}\)
9	\(\sqrt{9}=3\)

定义：数字的平方

定义：一个数字的平方根

定义：平方根表示法

示例\(\PageIndex{1}\)

示例\(\PageIndex{2}\)

示例\(\PageIndex{3}\)

示例\(\PageIndex{4}\)

示例\(\PageIndex{5}\)

示例\(\PageIndex{6}\)

示例\(\PageIndex{7}\)

示例\(\PageIndex{8}\)

示例\(\PageIndex{9}\)

示例\(\PageIndex{10}\)

示例\(\PageIndex{11}\)

示例\(\PageIndex{12}\)

示例\(\PageIndex{13}\)

示例\(\PageIndex{14}\)

示例\(\PageIndex{15}\)

示例\(\PageIndex{16}\)

示例\(\PageIndex{17}\)

示例\(\PageIndex{18}\)

示例\(\PageIndex{19}\)

示例\(\PageIndex{20}\)

示例\(\PageIndex{21}\)

示例\(\PageIndex{22}\)

示例\(\PageIndex{23}\)

示例\(\PageIndex{24}\)

示例\(\PageIndex{25}\)

示例\(\PageIndex{26}\)

示例\(\PageIndex{27}\)

示例\(\PageIndex{28}\)

示例\(\PageIndex{29}\)

示例\(\PageIndex{30}\)

示例\(\PageIndex{31}\)

示例\(\PageIndex{32}\)

示例\(\PageIndex{33}\)