8.6: 求解有理方程
- Page ID
- 204779
在本节结束时,您将能够:
- 求解有理方程
- 求解特定变量的有理方程
在 Foun@@ dations 的早期定义了表达式和方程式这两个术语之后,我们在整本书中都使用了它们。 我们简化了多种表达式并求解了许多种方程。 到目前为止,我们已经在本章中简化了许多有理表达式。 现在我们将求解有理方程。
有理方程的定义类似于我们在基础中使用的方程的定义。
有理方程是两个由等号连接的有理表达式。
你必须确保知道有理表达式和有理方程式之间的区别。 方程包含等号。
\[\begin{array}{cc} {\textbf{Rational Expression}}&{\textbf{Rational Equation}}\\ {\frac{1}{8}x+\frac{1}{2}}&{\frac{1}{8}x+\frac{1}{2}=\frac{1}{4}}\\ {\frac{y+6}{y^2−36}}&{\frac{y+6}{y^2−36}=y+1}\\ {\frac{1}{n−3}+\frac{1}{n+4}}&{\frac{1}{n−3}+\frac{1}{n+4}=\frac{15}{n^2+n−12}}\\ \nonumber \end{array}\]
求解有理方程
我们已经求解了包含分数的线性方程。 我们找到了方程中所有分数的 LCD,然后将方程的两边乘以 LCD 以 “清除” 分数。
以下是我们在处理线性方程时做的一个例子:
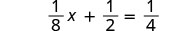 |
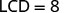 |
|
| 我们将两边乘以液晶屏。 | 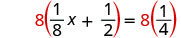 |
|
| 然后我们分发了东西。 | 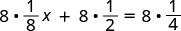 |
|
| 我们简化了——然后我们得到了一个没有分数的方程。 | 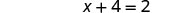 |
|
| 最后,我们求解了这个方程式。 | 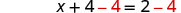 |
|
 |
我们将使用相同的策略来求解有理方程。 我们将等式的两边乘以液晶屏。 然后我们将得到一个不包含有理表达式的方程,因此我们更容易求解。
但是,由于原始方程可能在分母中有一个变量,因此我们必须小心,不要最终得到会使分母等于零的解。
因此,在我们开始求解有理方程之前,我们首先对其进行检查,以找到可以使任何分母为零的值。 这样,当我们求解有理方程时,我们就会知道是否有任何代数解必须丢弃。
会导致任何有理表达式未定义的有理方程的代数解被称为外来解。
有理方程的外来解是代数解,它会导致原始方程中的任何表达式未定义。
我们通过书面形式注意到任何可能的无关解决方案 c\(x \ne c\) next to the equation.
如何用有理表达式求解方程
解决:\(\frac{1}{x}+\frac{1}{3}=\frac{5}{6}\)。
- 回答
-

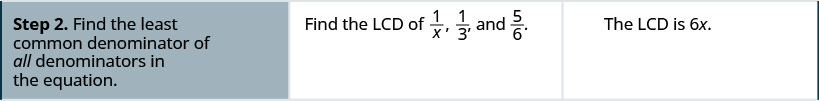



解决:\(\frac{1}{y}+\frac{2}{3}=\frac{1}{5}\)。
- 回答
-
\(−\frac{15}{7}\)
解决:\(\frac{2}{3}+\frac{1}{5}=\frac{1}{x}\)。
- 回答
-
\(\frac{15}{13}\)
此方法的步骤如下所示。
- 注意变量中任何会使任何分母变为零的值。
- 找出方程中所有分母的最小公分母。
- 通过将方程的两边乘以 LCD 来清除分数。
- 求解由此产生的方程。
- 查看。
- 如果在步骤 1 中找到的任何值是代数解,则将其丢弃。
- 检查原始方程中所有剩余的解。
首先,我们总是要注意会导致任何分母变为零的值。
解决:\(1−\frac{5}{y}=−\frac{6}{y^2}\)。
- 回答
-
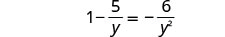
注意变量中任何会使任何分母变为零的值。 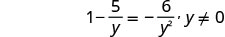
找出方程中所有分母的最小公分母。 液晶屏是\(y^2\) 通过将方程的两边乘以 LCD 来清除分数。 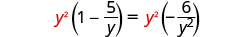
分发。 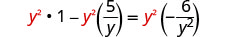
乘。 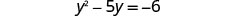
求解由此产生的方程。 首先用标准形式写出二次方程。 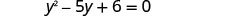
因子。 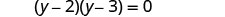
使用 “零积分” 属性。 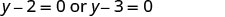
解决。 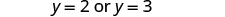
查看。 我们没有得到 0 作为代数解。 
解决:\(1−\frac{2}{a}=\frac{15}{a^2}\)。
- 回答
-
5, −3
解决:\(1−\frac{4}{b}=\frac{12}{b^2}\)。
- 回答
-
6, −2
解决:\(\frac{5}{3u−2}=\frac{3}{2u}\)。
- 回答
-
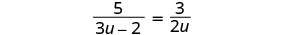
注意变量中任何会使任何分母变为零的值。 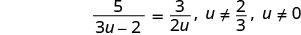
找出方程中所有分母的最小公分母。 液晶屏为 2u (3u−2)。 通过将方程的两边乘以 LCD 来清除分数。 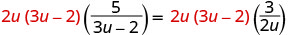
移除常见因素。 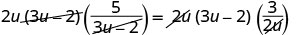
简化。 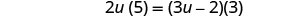
乘。 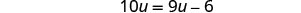
求解由此产生的方程。 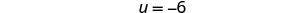
我们没有得到 0 或\(\frac{2}{3}\)作为代数解。 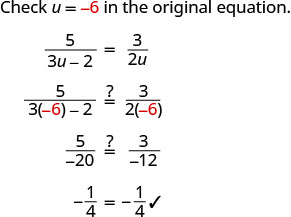
解决:\(\frac{1}{x−1}=\frac{2}{3x}\)。
- 回答
-
−2
解决:\(\frac{3}{5n+1}=\frac{2}{3n}\)。
- 回答
-
−2
当其中一个分母是二次时,记得先将其分数以找到 LCD。
解决:\(\frac{2}{p+2}+\frac{4}{p−2}=\frac{p−1}{p^2−4}\)。
- 回答
-
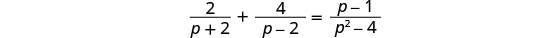
注意变量中任何会使任何分母变为零的值。 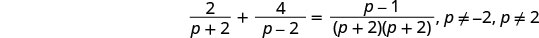
找出方程中所有分母的最小公分母。 液晶屏为 (p+2) (p−2)。 通过将方程的两边乘以 LCD 来清除分数。 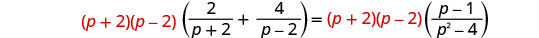
分发。 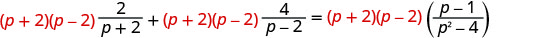
移除常见因素。 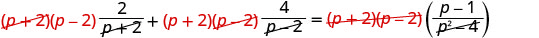
简化。 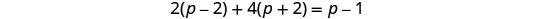
分发。 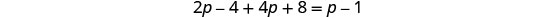
解决。 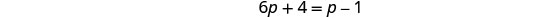


我们没有得到 2 或 −2 作为代数解。 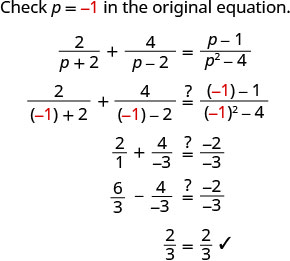
解决:\(\frac{2}{x+1}+\frac{1}{x−1}=\frac{1}{x^2−1}\)。
- 回答
-
\(\frac{2}{3}\)
解决:\(\frac{5}{y+3}+\frac{2}{y−3}=\frac{5}{y^2−9}\)
- 回答
-
2
解决:\(\frac{4}{q−4}−\frac{3}{q−3}=1\)。
- 回答
-

注意变量中任何会使任何分母变为零的值。 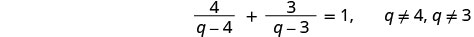
找出方程中所有分母的最小公分母。 液晶屏是 (q−4) (q−3)。 通过将方程的两边乘以 LCD 来清除分数。 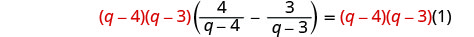
分发。 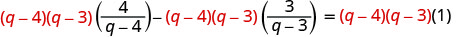
移除常见因素。 
简化。 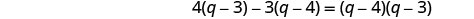
简化。 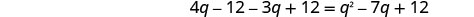
将相似的术语组合在一起。 
解决。 首先以标准形式编写。 
因子。 
使用 “零积分” 属性。 
我们没有得到 4 或 3 作为代数解。 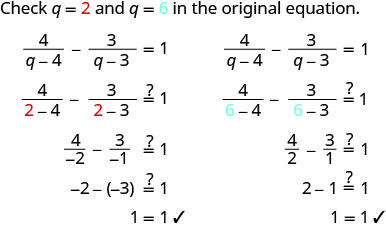
解决:\(\frac{2}{x+5}−\frac{1}{x−1}=1\)。
- 回答
-
−1、−2
解决:\(\frac{3}{x+8}−\frac{2}{x−2}=1\)。
- 回答
-
−2、−3
解决:\(\frac{m+11}{m^2−5m+4}=\frac{5}{m−4}−\frac{3}{m−1}\)。
- 回答
-
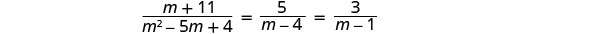
分解所有分母,这样我们就可以注意到变量的任何值都会使任何分母为零。 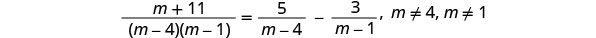
找出方程中所有分母的最小公分母。 液晶屏是 (m−4) (m−1) 清除分数。 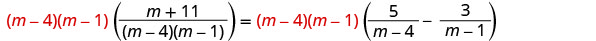
分发。 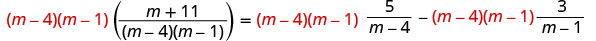
移除常见因素。 
简化。 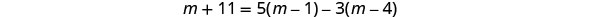
求解由此产生的方程。 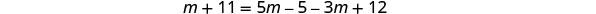

查看。 唯一的代数解是 4,但我们说过 4 会使分母等于零。 代数解是外来解。 这个方程没有解。
解决:\(\frac{x+13}{x^2−7x+10}=\frac{6}{x−5}−\frac{4}{x−2}\)。
- 回答
-
没有解决办法
解决:\(\frac{y−14}{y^2+3y−4}=\frac{2}{y+4}+\frac{7}{y−1}\)。
- 回答
-
没有解决办法
我们在示例中求解的方程只有一个代数解,但它是一个无关的解。 这使我们无法解决这个方程式。 有些方程没有解。
解决:\(\frac{n}{12}+\frac{n+3}{3n}=\frac{1}{n}\)。
- 回答
-
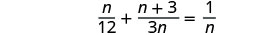
注意变量中任何会使任何分母变为零的值。 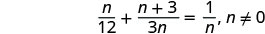
找出方程中所有分母的最小公分母。 液晶屏为 12n。 通过将方程的两边乘以 LCD 来清除分数。 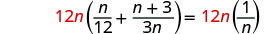
分发。 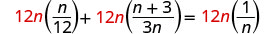
移除常见因素。 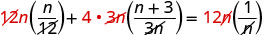
简化。 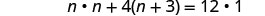
求解由此产生的方程。 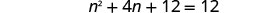
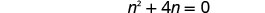
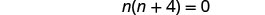
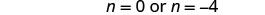
查看。 n=0 是一个无关的解。 
解决:\(\frac{x}{18}+\frac{x+6}{9x}=\frac{2}{3x}\)。
- 回答
-
−2
解决:\(\frac{y+5}{5y}+\frac{y}{15}=\frac{1}{y}\)。
- 回答
-
−3
解决:\(\frac{y}{y+6}=\frac{72}{y^2−36}+4\)。
- 回答
-
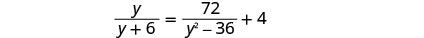
将所有分母分数分数分解,这样我们就可以记下变量中任何会使任何分母为零的值。 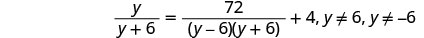
找出最小公分母。 液晶屏为 (y−6) (y+6)。 清除分数。 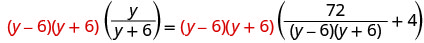
简化。 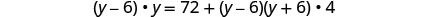
简化。 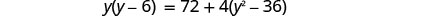
求解由此产生的方程。 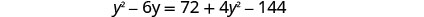
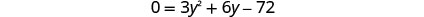
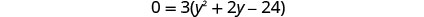
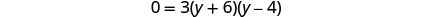
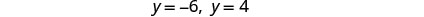
查看。 y=−6 是一个无关的解。 
解决:\(\frac{x}{x+4}=\frac{32}{x^2−16}+5\)。
- 回答
-
−4、3
解决:\(\frac{y}{y+8}=\frac{128}{y^2−64}+9\)。
- 回答
-
7
解决:\(\frac{x}{2x−2}−\frac{2}{3x+3}=\frac{5x^2−2x+9}{12x^2−12}\)。
- 回答
-
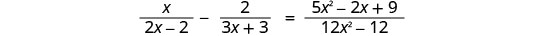
首先,我们将考虑所有分母,以便更容易识别无关的解决方案和液晶显示屏。 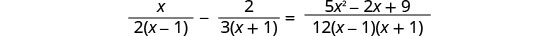
注意变量中任何会使任何分母变为零的值。 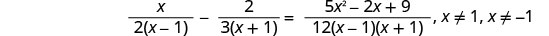
找出最小公分母。液晶屏为 12 (x−1) (x+1) 清除分数。 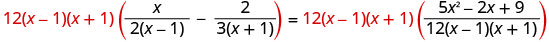
简化。 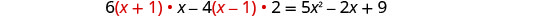
简化。 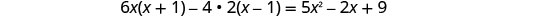
求解由此产生的方程。 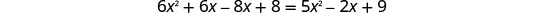
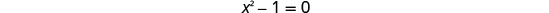
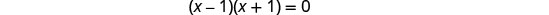
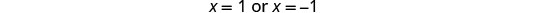
查看。 x=1 和 x=−1 是无关的解。
该方程没有解。
解决:\(\frac{y}{5y−10}−\frac{5}{3y+6}=\frac{2y^2−19y+54}{15y^2−60}\)。
- 回答
-
没有解决办法
解决:\(\frac{z^2}{z+8}−\frac{3}{4z−8}=\frac{3z^2−16z−68}{z^2+8z−64}\)。
- 回答
-
没有解决办法
求解特定变量的有理方程
当我们求解线性方程时,我们学会了如何求解特定变量的公式。 商业、科学、经济学和其他领域中使用的许多公式都使用有理方程来模拟两个或多个变量之间的关系。 现在,我们将看到如何求解特定变量的有理方程。
我们将从一个与距离、速率和时间相关的公式开始。 我们以前曾多次使用过它,但通常不以这种形式使用。
解决:\(\frac{D}{T}=R\)对于 T
- 回答
-
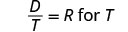
注意变量中任何会使任何分母变为零的值。 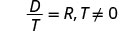
通过将方程的两边乘以 LCD T 来清除分数。 
简化。 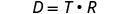
将两边除以 R 以分离 T。 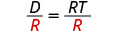
简化。 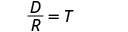
解决:\(\frac{A}{L}=W\)对于 L
- 回答
-
\(L=\frac{A}{W}\)
解决:\(\frac{F}{A}=M\)对于 A
- 回答
-
\(A=\frac{F}{M}\)
示例使用斜率公式,我们使用该公式得出直线方程的点斜率形式。
求解:f\(m=\frac{x−2}{y−3}\) or y。
- 回答
-
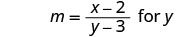
注意变量中任何会使任何分母变为零的值。 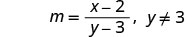
通过将方程的两边乘以 LCD y−3 来清除分数。 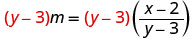
简化。 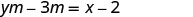
用 y 分离该项。 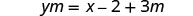
将两边除以 m 以分离 y。 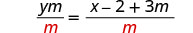
简化。 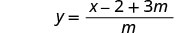
求解:\(\frac{y−2}{x+1}=\frac{2}{3}\)对于 x。
- 回答
-
\(x=\frac{3y−8}{2}\)
求解:f\(x=\frac{y}{1−y}\) or y。
- 回答
-
\(y=\frac{x}{1+x}\)
请务必按照示例中的所有步骤操作。 它可能看起来像一个非常简单的公式,但是对于任何一个分母,我们都无法立即求解。
\(\frac{1}{c}+\frac{1}{m}=1\)求解 c。
- 回答
-
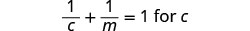
注意变量中任何会使任何分母变为零的值。 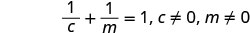
通过将方程的两边乘以 LCD 来清除分数,cm 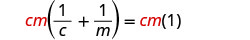
分发。 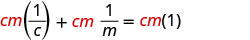
简化。 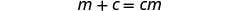
收集右侧带有 c 的条款。 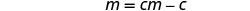
将右边的表达式分解为因子。 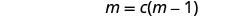
要分离 c,请将两边除以 m−1。 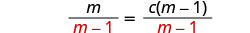
通过删除常见因素进行简化。 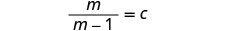
请注意,尽管我们从原始方程中排除了 c=0 和 m=0,但我们现在也必须说明这一点\(m \ne 1\)。
解决:\(\frac{1}{a}+\frac{1}{b}=c\)对于 a.
- 回答
-
\(a=\frac{b}{cb−1}\)
求解:f\(\frac{2}{x}+\frac{1}{3}=\frac{1}{y}\) or y。
- 回答
-
\(y=\frac{3x}{6+x}\)
关键概念
- 用有理表达式求解方程的策略
- 注意变量中任何会使任何分母变为零的值。
- 找出方程中所有分母的最小公分母。
- 通过将方程的两边乘以 LCD 来清除分数。
- 求解由此产生的方程。
- 查看。
- 如果在步骤 1 中找到的任何值是代数解,则将其丢弃。
- 检查原始方程中所有剩余的解。
词汇表
- 有理方程
- 有理方程是两个由等号连接的有理表达式。
- 有理方程的外来解
- 有理方程的外来解是代数解,它会导致原始方程中的任何表达式未定义。


