8.4:使用不同分母加减有理表达式
- Page ID
- 204881
在本节结束时,您将能够:
- 找出有理表达式的最小公分母
- 找到等效的有理表达式
- 添加具有不同分母的有理表达式
- 减去具有不同分母的有理表达式
在开始之前,请参加这个准备测验。
如果您遗漏了问题,请返回列出的部分并查看材料。
- 添加:\(\frac{7}{10}+\frac{8}{15}\)。
如果您错过了此问题,请查看练习 1.7.13。 - 减去:\(6(2x+1)−4(x−5)\)。
如果你错过了这个问题,请查看练习 1.10.52。 - 找出最大的共同因素\(9x^{2}y^{3}\),\(12xy^{5}\)
如果你错过了这个问题,请查看练习 7.1.7。 - 完全考虑 −48n−12
如果你错过了这个问题,请查看练习 7.1.31。
找出有理表达式的最小公分母
当我们加上或减去具有不同分母的有理表达式时,我们需要得到公分母。 如果我们回顾一下我们使用数字分数的程序,我们就会知道如何处理有理表达式。
让我们来看看基金会\(\frac{7}{12}+\frac{5}{18}\)的例子。 由于分母不同,第一步是找到最小公分母 (LCD)。 请记住,液晶屏是分母中最不常见的倍数。 这是我们可以用作公分母的最小数字。
为了找出 12 和 18 的 LCD,我们将每个数字分解为素数,将所有常见的素数排成列。 然后我们从每列中 “降低” 一个素数。 最后,我们将这些因子相乘得出液晶屏。
12=2·2·3
18=2·3·3
LCD=2·2·3·3
LCD=36
对于理性表达,我们也做同样的事情。 但是,我们将液晶屏保留为保值形式。
- 对每个表达式进行完全分解。
- 列出每个表达式的因子。 尽可能垂直匹配因子。
- 把柱子放下。
- 将因子相乘。
请记住,我们总是排除会使分母为零的值。 在下一个示例中,我们应该排除 xv 的哪些值?
找到液晶显示屏\(\frac{8}{x^2−2x−3}\),\(\frac{3x}{x^2+4x+3}\)
- 回答
-
\(\frac{8}{x^2−2x−3}\),\(\frac{3x}{x^2+4x+3}\) 对每个表达式进行全面分解,列出共同因子。 把柱子放下。 \(x^2−2x−3=(x−3)(x+1)\) \(x^2+4x+3=(x+1)(x+3)\) 将因子相乘。 LCD= (x+1) (x−3) (x+3) 液晶屏是 (x+1) (x−3) (x+3)。
找到适合的液晶屏\(\frac{2}{x^2−x−12},\frac{1}{x^2−16}\)
- 回答
-
(x−4) (x+4) (x+3)
找到适合的液晶屏\(\frac{x}{x^2+8x+15},\frac{5}{x^2+9x+18}\)
- 回答
-
(x+3) (x+6) (x+5)
查找等效有理表达式
当我们添加数值分数时,一旦找到液晶屏,我们就会将每个分数重写为与液晶屏等效的分数。
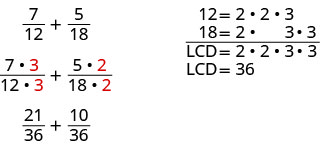
对于理性表达,我们将做同样的事情。
使用分母 (x+1) (x−3) (x+3) 重写为等效有理表达式:\(\frac{8}{x^2−2x−3}\),\(\frac{3x}{x^2+4x+3}\)。
- 回答
-
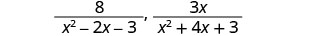
将每个分母分母除外。 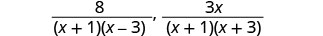
找到液晶屏。 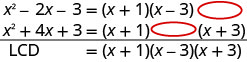
将每个分母乘以 “缺失” 因子,然后将每个分子乘以相同的因子。 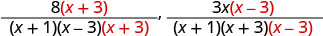
简化分子。 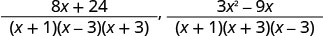
使用分母 (x+3) (x−4) (x+4) 重写为等效有理表达式:
\(\frac{2}{x^2−x−12}\),\(\frac{1}{x^2−16}\)。
- 回答
-
\(\frac{2x+8}{(x−4)(x+3)(x+4)}\),
\(\frac{x+3}{(x−4)(x+3)(x+4)}\)
使用分母 (x+3) (x+5) (x+6)
\(\frac{x}{x^2+8x+15}\) 重写为等效有理表达式\(\frac{5}{x^2+9x+18}\)。
- 回答
-
\(\frac{x^2+6x}{(x+3)(x+5)(x+6)}\),
\(\frac{x+3}{(x+3)(x+5)(x+6)}\)
添加具有不同分母的有理表达式
现在我们有了添加具有不同分母的有理表达式所需的所有步骤。 正如我们之前所做的那样,我们将举一个先添加数字分数的示例。
添加:\(\frac{7}{12}+\frac{5}{18}\)。
- 回答
-
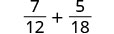
找到 12 和 18 的液晶屏。 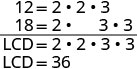
使用液晶屏将每个分数重写为等效分数。 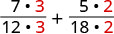
添加分数。 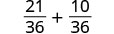
分数无法简化。 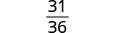
添加:\(\frac{11}{30}+\frac{7}{12}\)。
- 回答
-
\(\frac{19}{20}\)
添加:\(\frac{3}{8}+\frac{9}{20}\)。
- 回答
-
\(\frac{33}{40}\)
现在我们将添加分母为单项式的有理表达式。
添加:\(\frac{5}{12x^{2}y}+\frac{4}{21xy^2}\)。
- 回答
-
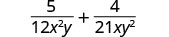
找到\(12x^{2}y\)和的液晶屏\(21xy^2\)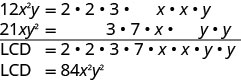
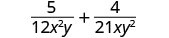
使用 LCD 将每个有理表达式重写为等效分数。 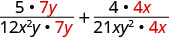
简化。 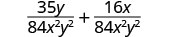
添加有理表达式。 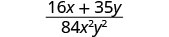
分子和分母没有共同的因子。 分数无法简化。
添加:\(\frac{2}{15a^{2}b}+\frac{5}{6ab^2}\)。
- 回答
-
\(\frac{4b+25a}{30a^{2}b^2}\)
添加:\(\frac{5}{16c}+\frac{3}{8cd^2}\)。
- 回答
-
\(\frac{5d^2+6}{16cd^2}\)
现在我们已经准备好解决多项式分母了。
如何添加具有不同分母的有理表达式
添加:\(\frac{3}{x−3}+\frac{2}{x−2}\)。
- 回答
-



添加:\(\frac{2}{x−2}+\frac{5}{x+3}\)。
- 回答
-
\(\frac{7x−4}{(x+3)(x−2)}\)
添加:\(\frac{4}{m+3}+\frac{3}{m+4}\)。
- 回答
-
\(\frac{7m+25}{(m+3)(m+4)}\)
以下过程框中总结了用于添加有理表达式的步骤。
- 确定表达式是否有公分母。
是-转到步骤 2。
否 — 使用 LCD 重写每个有理表达式。
找到液晶屏。
使用 LCD 将每个有理表达式重写为等效的有理表达式。 - 添加有理表达式。
- 如果可能,请简化。
添加:\(\frac{2a}{2ab+b^2}+\frac{3a}{4a^2−b^2}\)。
- 回答
-
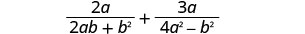
这些表达式有共同点吗? 不是。
使用 LCD 重写每个表达式。找到液晶屏。 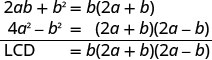
使用 LCD 将每个有理表达式重写为等效的有理表达式。 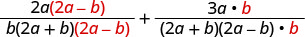
简化分子。 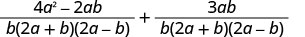
添加有理表达式。 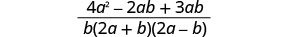
简化分子。 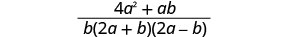
将分子分解为因子。 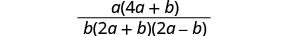
分子和分母没有共同的因子。 分数无法简化。
添加:\(\frac{5x}{xy−y^2}+\frac{2x}{x^2+y^2}\)。
- 回答
-
\(\frac{x(5x+7y)}{y(x−y)(x+y)}\)
添加:\(\frac{7}{2m+6}+\frac{4}{m^2+4m+3}\)。
- 回答
-
\(\frac{7m+15}{2(m+3)(m+1)}\)
避免过早简化的诱惑! 在上面的例子中,我们必须将第一个有理表达式保留为\(\frac{2a(2a−b)}{b(2a+b)(2a−b)}\) to be able to add it to \(\frac{3a·b}{(2a+b)(2a−b)·b}\).
添加:\(\frac{8}{x^2−2x−3}+\frac{3x}{x^2+4x+3}\)。
- 回答
-
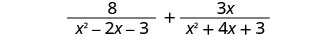
这些表达式有共同点吗? 不是。
使用 LCD 重写每个表达式。找到液晶屏。 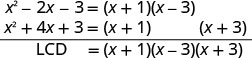
使用 LCD 将每个有理表达式重写为等效分数。 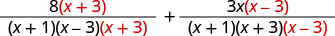
简化分子。 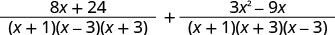
添加有理表达式。 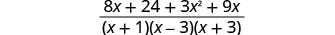
简化分子。 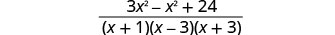
分子是素数,因此没有常见的因子。
添加:\(\frac{1}{m^2−m−2}+\frac{5m}{m^2+3m+2}\)。
- 回答
-
\(\frac{5m^2−9m+2}{(m−2)(m+1)(m+2)}\)
添加:\(\frac{2n}{n^2−3n−10}+\frac{6}{n^2+5n+6}\)。
- 回答
-
\(\frac{2(n2+6n−15)}{(n+2)(n−5)(n+3)}\)
减去具有不同分母的有理表达式
我们用来减去具有不同分母的有理表达式的过程与加法的过程相同。 在减去分子时,我们只需要非常小心符号即可。
如何用不同的分母减去有理表达式
减去:\(\frac{x}{x−3}−\frac{x−2}{x+3}\)。
- 回答
-



减去:\(\frac{y}{y+4}−\frac{y−2}{y−5}\)。
- 回答
-
\(\frac{−7y+8}{(y+4)(y−5)}\)
减去:\(\frac{z+3}{z+2}−\frac{z}{z+3}\)。
- 回答
-
\(\frac{4z+9}{(z+2)(z+3)}\)
下面列出了减去有理表达式的步骤。
- 确定它们是否有共同点。
是-转到步骤 2。
否 — 使用 LCD 重写每个有理表达式。
找到液晶屏。
使用 LCD 将每个有理表达式重写为等效的有理表达式。 - 减去有理表达式。
- 如果可能,请简化。
减去:\(\frac{8y}{y^2−16}−\frac{4}{y−4}\)。
- 回答
-
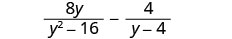
这些表达式有共同点吗? 不是。
使用 LCD 重写每个表达式。找到液晶屏。 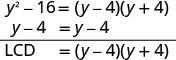
使用 LCD 将每个有理表达式重写为等效的有理表达式。 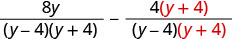
简化分子。 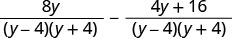
减去有理表达式。 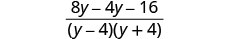
简化分子。 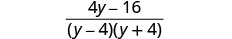
将分子分解以寻找常见因子。 
移除常见因素。 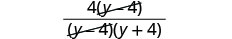
简化。 
减去:\(\frac{2x}{x^2−4}−\frac{1}{x+2}\)。
- 回答
-
\(\frac{1}{x−2}\)
减去:\(\frac{3}{z+3}−\frac{6z}{z^2−9}\)。
- 回答
-
\(\frac{−3}{z−3}\)
下一个例子中有很多负面信号。 要格外小心!
减去:\(\frac{−3n−9}{n^2+n−6}−\frac{n+3}{2−n}\)。
- 回答
-
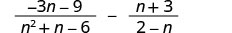
将分母考虑在内。 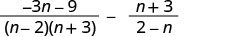
由于 n−2 和 2−n 是对立的,我们将第二个有理表达式乘以\(\frac{−1}{−1}\)。 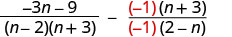
简化。 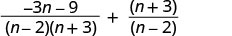
这些表达式有共同点吗? 不是。 找到液晶屏。 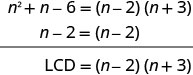
使用 LCD 将每个有理表达式重写为等效的有理表达式。 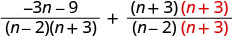
简化分子。 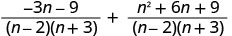
简化有理表达式。 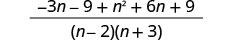
简化分子。 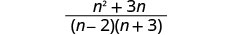
将分子分解以寻找常见因子。 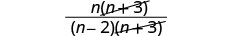
简化。 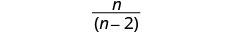
减去:\(\frac{3x−1}{x^2−5x−6}−\frac{2}{6−x}\)。
- 回答
-
\(\frac{1}{x−6}\)
减去:\(\frac{−2y−2}{y^2+2y−8}−\frac{y−1}{2−y}\)。
- 回答
-
\(\frac{y+3}{y+4}\)
当一个表达式不是分数形式时,我们可以将其写成分母为 1 的分数。
减去:\(\frac{5c+4}{c−2}−3\)。
- 回答
-
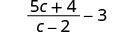
写 3 as\(\frac{3}{1}\) 就有 2 个有理表达式。 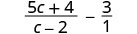
有理表达式有共同点吗? 不是。 找到 c−2 和 1 的液晶屏。 液晶屏 = c−2。 重写\(\frac{3}{1}\)为与 LCD 等效的有理表达式。 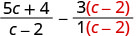
简化。 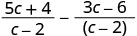
减去有理表达式。 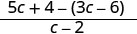
简化。 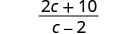
检查常见因素的因子。 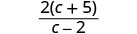
没有共同的因素;理性表达方式被简化了。
减去:\(\frac{2x+1}{x−7}−3\)。
- 回答
-
\(\frac{−x+22}{x−7}\)
减去:\(\frac{4y+3}{2y−1}−5\)。
- 回答
-
\(\frac{−2(3y−4)}{2y−1}\)
- 确定表达式是否有公分母。
是-转到步骤 2。
否 — 使用 LCD 重写每个有理表达式。
找到液晶屏。
使用 LCD 将每个有理表达式重写为等效的有理表达式。 - 加上或减去有理表达式。
- 如果可能,请简化。
当我们有两个以上的有理表达式时,我们会按照与以前相同的步骤找到液晶屏。 在下一个示例中,我们将首先分解所有三个分母以找到它们的液晶显示屏。
简化:\(\frac{2u}{u−1}+\frac{1}{u}−\frac{2u−1}{u^2−u}\)。
- 回答
-
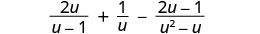
有理表达式有共同点吗? 不是。 找到液晶屏。 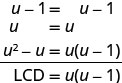
使用 LCD 将每个有理表达式重写为等效的有理表达式。 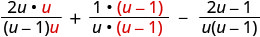
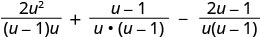
写成一个理性表达。 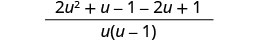
简化。 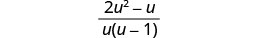
将分子分解并移除常见因子。 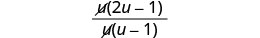
简化。 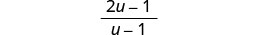
简化:\(\frac{v}{v+1}+\frac{3}{v−1}−\frac{6}{v^2−1}\)。
- 回答
-
\(\frac{v+3}{v+1}\)
在此处添加练习文本。简化:\(\frac{3w}{w+2}+\frac{2}{w+7}−\frac{17w+4}{w^2+9w+14}\)。
- 回答
-
\(\frac{3w}{w+7}\)
关键概念
- 找出有理表达式的最小公分母
- 对每个表达式进行完全分解。
- 列出每个表达式的因子。 尽可能垂直匹配因子。
- 把柱子放下。
- 将因子相乘。
- 添加或减去有理表达式
- 确定表达式是否有公分母。
是-转到步骤 2。
否 — 使用 LCD 重写每个有理表达式。- 找到液晶屏。
- 使用 LCD 将每个有理表达式重写为等效的有理表达式。
- 加上或减去有理表达式。
- 如果可能,请简化。
- 确定表达式是否有公分母。


