5.3: 指数分布

指数分布通常与某个特定事件发生之前的时间长短有关。 例如，地震发生之前的时间（从现在开始）呈指数分布。 其他示例包括长途商务电话通话的时间长度（以分钟为单位），以及汽车电池的使用时间（以月为单位）。 也可以看出，你口袋或钱包里的零钱的价值大致遵循指数分布。

指数随机变量的值按以下方式出现。 大值越少，小值越多。 例如，市场研究表明，顾客在一次超市旅行中花费的金额呈指数级分布。 花少量钱的人越来越多，花大量钱的人更少。

指数分布通常用于计算产品可靠性或产品持续时间长度。

指数分布的随机变量是连续的，通常用于测量时间的流逝，尽管它可用于其他应用程序。 典型的问题可能是：“某些事件在接下来的\(x\)几个小时或几天内发生的概率是多少，或者某些事件在几\(x_1\)小时和\(x_2\)几小时之间发生的概率是多少，或者该事件需要超过\(x_1\)几个小时才能执行的概率是多少？” 简而言之，随机变量\(X\)等于 (a) 事件之间的时间或 (b) 完成动作的时间间隔，例如等待客户。 概率密度函数由以下公式给出：

\[f(x)=\frac{1}{\mu} e^{-\frac{1}{\mu} x}\nonumber\]

哪里\(\mu\)是历史平均等待时间。

且均值和标准差均为\(1/\mu\)。

指数分布公式的另一种形式可识别通常称为衰减因子的因素。 衰减因子只是衡量随机变量的\(X\)增加事件的概率下降的速度。 当使用使用衰减参数 m 的表示法时，概率密度函数表示为：

\[f(x)=m e^{-m x}\nonumber\]

哪里\(m=\frac{1}{\mu}\)

为了计算特定概率密度函数的概率，使用累积密度函数。 累积密度函数 (cdf) 只是 pdf 的积分，为：

\[F(x)=\int_{0}^{\infty}\left[\frac{1}{\mu} e^{-\frac{x}{\mu}}\right]=1-e^{-\frac{x}{\mu}}\nonumber\]

示例\(\PageIndex{3}\)

Let\(X\) = 邮局职员与客户共处的时间（以分钟为单位）。 根据历史数据，该时间的平均时间等于四分钟。

假设\(\mu = 4\)分钟数，也就是说，店员与客户在一起的平均时间为4分钟。 请记住，我们还在计算概率，因此我们必须被告知总体参数，例如均值。 要进行任何计算，我们需要知道分布的平均值：例如，提供服务的历史时间。 知道历史平均值可以计算衰减参数 m。

\(m=\frac{1}{\mu}\)。 因此，\(m=\frac{1}{4}=0.25\)。

当表示法使用衰减参数 m 时，概率密度函数表示为\(f(x)=m e^{-m x}\)，这只是用 m 代替或的原始公式\(f(x)=\frac{1}{\mu} e^{-\frac{1}{\mu} x}\)。\(\frac{1}{\mu}\)

要计算指数概率密度函数的概率，我们需要使用累积密度函数。 如下所示，累积密度函数的曲线为：

\(f(x) = 0.25e^{–0.25x}\)其中 x 至少为零，并且\(m = 0.25\)。

例如，\(f(5) = 0.25e^{(-0.25)(5)} = 0.072\)。 换句话说，当时，该函数的值为 .072\(x = 5\)。

图表如下所示：

图\(\PageIndex{13}\)

请注意，该图是一条下降的曲线。 什么时候\(x = 0\)，

\(f(x) = 0.25e^{(−0.25)(0)} = (0.25)(1) = 0.25 = m\)。 y 轴上的最大值始终\(m\)为 1 除以均值。

练习\(\PageIndex{3}\)

配偶购买周年纪念卡的时间可以通过指数分布进行建模，平均时间等于八分钟。 写下分布，陈述概率密度函数，然后绘制分布图。

示例\(\PageIndex{4}\)

a. 使用示例中的信息\(\PageIndex{3}\)，计算业务员与随机选择的客户共度四到五分钟的概率。

回答

a. 查找\(P (4 < x < 5)\)。
累积分布函数 (CDF) 给出了左边的面积。
\(P(x < x) = 1 – e^{–mx}\)
\(P(x < 5) = 1 – e^{(–0.25)(5)} = 0.7135\)和\(P(x < 4) = 1 – e^{(–0.25)(4)} = 0.6321\)
\(P(4 < x < 5)= 0.7135 – 0.6321 = 0.0814\)

图 5.14

练习\(\PageIndex{4}\)

旅客提前购买机票的天数可以通过指数分布建模，平均时间等于 15 天。 找出旅行者提前不到十天购买机票的可能性。 一半的旅客要等多少天？

示例\(\PageIndex{5}\)

平均而言，某一计算机部件的使用寿命为十年。 计算机部分持续的时间长度呈指数分布。

a. 计算机部件的使用寿命超过 7 年的概率是多少？

回答

a. 让\(x =\)计算机部件持续的时间（以年为单位）。
\ mu = 10 所以\(m=\frac{1}{\mu}=\frac{1}{10}=0.1\)
查找\(P(x > 7)\)。 绘制图表。
\(P(x > 7) = 1 – P(x < 7)\)。
从\(P(X < x) = 1 – e^{–mx}\)那以后\(P(X > x) = 1 – ( 1 –^{e–mx}) = e^{–mx}\)
\(P(x > 7) = e(–0.1)(7) = 0.4966\)。 计算机部件的使用寿命超过七年的概率是\(0.4966\)。

图\(\PageIndex{15}\)

b. 平均而言，如果五个计算机部件一个接一个地使用，它们能持续多久？

回答

b. 平均而言，一个计算机部件的使用寿命为十年。 因此，五个计算机部件，如果一个接一个地使用，平均使用寿命（5）（10）= 50 年。

d. 计算机部件的使用寿命在 9 到 11 年之间的概率是多少？

回答

d. 查找\(P (9 < x < 11)\)。 绘制图表。

图\(\PageIndex{16}\)

\(P(9 < x < 11) = P(x < 11) – P(x < 9) = (1 – e^{(–0.1)(11)}) – (1 – e^{(–0.1)(9)}) = 0.6671 – 0.5934 = 0.0737\)。 计算机部件的使用寿命在 9 到 11 年之间的概率为\(0.0737\)。

练习\(\PageIndex{5}\)

平均而言，如果每天使用，一双跑鞋可以持续 18 个月。 跑鞋的使用时间长度呈指数分布。 一双跑鞋的使用寿命超过 15 个月的概率是多少？ 平均而言，如果一个接一个地使用六双跑鞋，它们能持续多长时间？ 如果每天使用，百分之八十的跑鞋最多能持续多长时间？

示例\(\PageIndex{6}\)

假设电话的长度（以分钟为单位）是一个带有衰减参数的指数随机变量\(\frac{1}{12}\)。 衰变 p [参数是查看 1/l 的另一种方式。 如果另一个人在你之前接到公用电话，你可能需要等待五分钟以上。 假设 X = 通话时长，以分钟为单位。

什么是\(m, \mu\)，和\(\sigma\)？ 您必须等待五分钟以上的概率为 _______。

回答

\(m = \frac{1}{12}\)

\(\mu = 12\)

\(\sigma = 12\)

\(P(x > 5) = 0.6592\)

示例\(\PageIndex{7}\)

事件之间等待所花费的时间通常使用指数分布进行建模。 例如，假设平均每小时有 30 名顾客到达一家商店，并且两次到达之间的时间呈指数分布。

1. 平均而言，两次连续抵达之间要经过多少分钟？
2. 当商店首次开业时，三个顾客平均需要多长时间才能到达？
3. 在客户到达后，找出下一位客户到达所需时间不到一分钟的概率。
4. 在客户到达后，找出下一个客户需要超过五分钟才能到达的概率。
5. 在这种情况下，指数分布是否合理？

回答

a. 由于我们预计每小时（60 分钟）有 30 位客户到达，因此我们预计平均每两分钟就有一位客户到达。

b. 由于平均每两分钟就有一位顾客到达，因此三个客户平均需要六分钟才能到达。

c. 让\(X =\)两次到达之间的时间以分钟为单位。 按a部分来看\(\mu = 2\)，所以\(m = \frac{1}{2}= 0.5\)。
\(P(X < x) = 1 – e^{(-0.5)(x)}\)
因此，累积分布函数为\(P(X < 1) = 1 – e^{(–0.5)(1)} = 0.3935\)。

图\(\PageIndex{17}\)

d\(P(X > 5) = 1 – P(X < 5) = 1 – (1 – e^{(-0.5)(5)}) = e^{–2.5} \approx 0.0821\)。

图\(\PageIndex{18}\)

该模型假设一次只有一个顾客到达，这可能不合理，因为人们可能会成群购物，从而导致多个顾客同时到达。 它还假设客户流量在一天中没有变化，如果一天中的某些时间比其他时间更繁忙，则这是无效的。

指数分布的记忆力差

回想一下，前面讨论的邮递员在客户之间的时间是指数分布的，平均为两分钟。 假设距离最后一位客户到达已经过去了五分钟。 由于现在已经过去了异常长的时间，买家似乎更有可能在下一分钟内到达。 在指数分布中，情况并非如此——等待下一个客户所花费的额外时间并不取决于自上一个客户以来已经过去了多长时间。 这被称为无记忆属性。 指数和几何概率密度函数是唯一具有无记忆属性的概率函数。 具体来说，无记忆属性就是这样说的

\(P(X > r + t | X > r) = P (X > t)\)为所有人\(r \geq 0\)和\(t \geq 0\)

例如，如果自最后一位客户到达以来已经过去了五分钟，则在上述方程中使用 r = 5 和 t = 1 来计算下一个客户到达之前经过一分钟以上的概率。

\(P(X > 5 + 1 | X > 5) = P(X > 1) = e^{(-0.5)(1)} = 0.6065\)。

这与买家在上次抵达后等待超过一分钟才到达的概率相同。

指数分布通常用于模拟电气或机械设备的寿命。 在示例中\(\PageIndex{5}\)，某个计算机部件的寿命具有指数分布，平均值为十年。 无记忆的属性表明，了解过去发生的事情对未来的概率没有影响。 在这种情况下，这意味着旧部件在任何特定时间发生故障的可能性不大于全新零件。 换句话说，零件在突然坏掉之前一直保持新的一样。 例如，如果零件已经持续了十年，则它再持续七年的概率为\(P(X > 17|X > 10) = P(X > 7) = 0.4966\)，其中垂直线被读为 “给定”。

示例\(\PageIndex{8}\)

再次请回信给邮务员，其中邮政职员与客户在一起的时间呈指数分布，平均为四分钟。 假设一位客户与邮政员共度了四分钟。 他或她与邮政职员至少再待三分钟的可能性是多少？

的衰减参数\(X\)为\(m = \frac{1}{4} = 0.25\)，所以\(X \sim Exp(0.25)\)。

累积分布函数为\(P(X < x) = 1 – e^{–0.25x}\)。

我们想找到\(P (X > 7|X > 4)\)。 无记忆的房产说明了这一点\(P (X > 7|X > 4) = P (X > 3)\)，所以我们只需要找出客户与邮政服务员在一起的时间超过三分钟的概率即可。

这是\(P(X > 3) = 1 – P(X < 3) = 1 – (1 – e^{–0.25⋅3}) = e^{–0.75} \approx 0.4724\)。

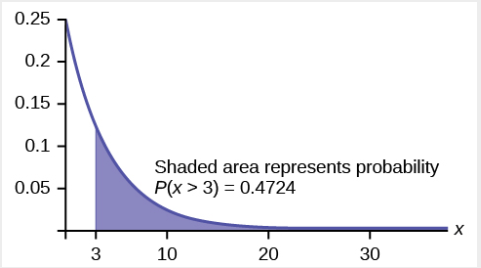
图\(\PageIndex{19}\)

泊松和指数分布之间的关系

指数分布和泊松分布之间有一种有趣的关系。 假设两个连续事件之间经过的时间遵循指数分布，平均值为时间\(\mu\)单位。 还要假设这些时间是独立的，这意味着事件之间的时间不受前一个事件之间的时间的影响。 如果这些假设成立，则每单位时间的事件数遵循泊松分布，均值\(\mu\)。 回想一下\(X\)，如果泊松分布与均值相\(\mu\)等，那么\(P(X=x)=\frac{\mu^{x_{e}-\mu}}{x !}\)。

指数分布的公式：\(P(X=x)=m e^{-m x}=\frac{1}{\mu} e^{-\frac{1}{\mu} x}\)其\(m =\)中，速率参数或两次出现之间的\(\mu =\)平均时间。

我们看到指数是泊松分布的表亲，它们通过这个公式相互关联。 有一些重要的差异使得每种分布与不同类型的概率问题相关。

首先，泊松有一个离散的随机变量\(x\)，其中时间；连续变量被人为地分解成离散的片段。 我们看到，给定时间间隔内事件的发生次数遵循泊松分布。\(x\)

例如，电话每小时响铃的次数。 相比之下，两次发生的时间遵循指数分布。 例如。 电话刚刚响了，还需要多久才能再次响起？ 我们测量的是区间的时间长度，这是一个连续的随机变量，指数变量，而不是间隔内的事件，泊松。

指数分布与泊松分布

显示这两个分布之间相似之处和不同之处的一种视觉方式是使用时间表。

图 5.20

泊松分布的随机变量是离散的，因此将给定时间段内的事件计数\(t_1\)到图\(t_2\)上\(\PageIndex{20}\)，并计算该数字发生的概率。 事件数（图中的四个）是用计数数来衡量的；因此，泊松的随机变量是一个离散的随机变量。

指数概率分布计算时间流逝的概率，这是一个连续的随机变量。 在图\(\PageIndex{20}\)中，它显示为从 t ₁ 到下一次出现的事件的括号，用三角形标记。

经典的 Poisson 配送问题是 “接下来的一个小时内有多少人会到达我的结账窗口？”。

经典的指数分布问题是 “下一个人到来需要多长时间”，或者一个变体，“这个人到达后会在这里待多久？”。

再说一遍，指数分布的公式是：

\[f(x)=m e^{-m x} \operatorname{orf}(x)=\frac{1}{\mu} e^{-\frac{1}{\mu} x}\nonumber\]

我们立即看到指数公式和泊松公式之间的相似之处。

\[P(x)=\frac{\mu^{x} e^{-\mu}}{x !}\nonumber\]

这两个概率密度函数都基于时间与指数增长或衰减之间的关系。 公式中的 “e” 是一个近似值为 2.71828 的常数，是自然对数指数增长公式的基础。 当人们说某件事呈指数级增长时，这就是他们所说的。

以指数和泊松为例，可以清楚地表明两者之间的区别。 它还将显示他们拥有的有趣应用程序。

泊松分布

假设历史上每小时有 10 位客户到达结账排队。 请记住，这仍然是概率，所以我们必须被告知这些历史值。 我们看到这是一个泊松概率问题。

我们可以将这些信息放入泊松概率密度函数中，然后得到一个通用公式，该公式将计算任何特定数量的客户在接下来的一个小时内到达的概率。

该公式适用于我们选择的随机变量的任何值，因此 x 被放入公式中。 这是公式：

\[f(x)=\frac{10^{x} e^{-10}}{x !}\nonumber\]

举个例子，在接下来的一个小时内有 15 个人到达结账柜台的概率为

\[P(x=15)=\frac{10^{15} e^{-10}}{15 !}=0.0611\nonumber\]

这里我们插入了 x = 15，并计算出在接下来的一个小时内有 15 个人到达的概率为 0.061。

指数分布

如果我们保持相同的历史事实，即每小时有 10 位客户到达，但我们现在对一个人在柜台花费的服务时间感兴趣，那么我们将使用指数分布。 对于这个特定的结账计数器历史数据，任何值 x（随机变量）的指数概率函数为：

\[f(x)=\frac{1}{.1} e^{-x / 1}=10 e^{-10 x}\nonumber\]

为了计算\(\mu\)历史平均服务时间，我们只需将每小时到达的人数 10 除以时间段（一小时和有）\(\mu = 0.1\)。 从历史上看，人们在结账柜台花费0.1小时，或6分钟。 这解释了公式中的 .1。

泊松公式和指数公式自然会混淆。\(\mu\) 尽管它们具有相同的符号，但它们具有不同的含义。 指数的均值等于一除以泊松的均值。 如果给出历史抵达人数，则得出泊松的平均值。 如果给出事件之间的历史时间长度，则平均值为指数。

继续以结账员为例；如果我们想知道一个人花9分钟或更少的时间结账的可能性，那么我们使用这个公式。 首先，我们将转换为相同的时间单位，即一小时的一部分。 九分钟等于一小时的 0.15。 接下来我们注意到我们要求的是一系列值。 连续随机变量总是如此。 我们将概率问题写成：

\[p(x \leq 9)=1-10 e^{-10 x}\nonumber\]

现在，我们可以将数字放入公式中，我们就有了结果。

\[p(x=.15)=1-10 e^{-10(.15)}=0.7769\nonumber\]

客户花9分钟或更少的时间结账的概率是\(0.7769\)。

我们看到，我们很有可能在不到九分钟的时间内离开，而在接下来的一个小时内有 15 位客户到达的可能性很小。