4.4: 线性函数
- Page ID
- 171242
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
线性函数是具有以下形式的函数\(f(x) = mx+b\)。 任何可以用表单表示的行也\(y = mx + b\)是一个函数。
当以 Slope-Intercept 形式书写的直线方程没有间隙或中断并且该直线不是垂直线时，请使用函数表示法。 写成\(f(x) = mx + b\)通过垂直线测试的线性函数：
垂直线测试用于确定图形是否将垂直输出定义为水平输入的函数。 如果任何垂直线会多次穿过图形，则图形不会为每个水平输入仅定义一个垂直输出。
有关线性方程的更多信息，请参阅直线部分。
创建解表并绘制以下线性函数的图形：
\(f(x) = 2x − 3\)
解决方案
\(f(x) = 2x − 3\)
要找到两个有序对，请选择小值\(x\)，然后计算值\(f(x)\)。
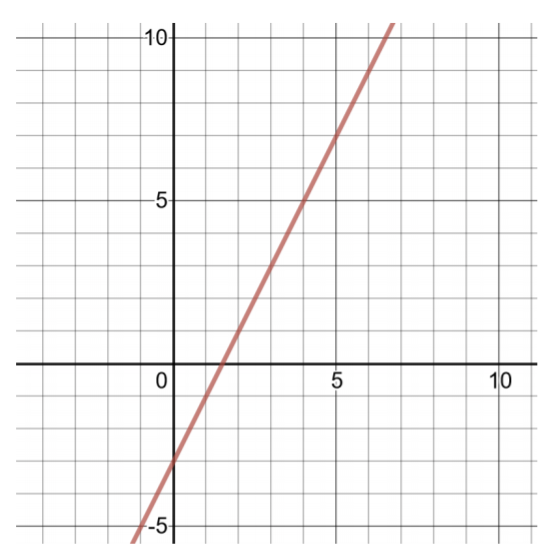
| 的解决方案表\(f(x) = 2x − 3\) | |
| \(x\) | \(f(x)\) |
| -1 | \(f(−1) = 2(−1) − 3 = −2 − 3 = −5\) |
| 0 | \(f(0) = 2(0) − 3 = 0 − 3 = 3\) |
创建解表并绘制以下线性函数的图形：
\(g(x) = \dfrac{1}{ 3} x + 4\)
解决方案
要找到两个有序对，请选择 x 的小值，然后计算的值\(g(x)\)。 由于包含 x 的项的系数是分数，因此请选择分母的倍数，\(\dfrac{1 }{3} x\)使的乘积成为整数。
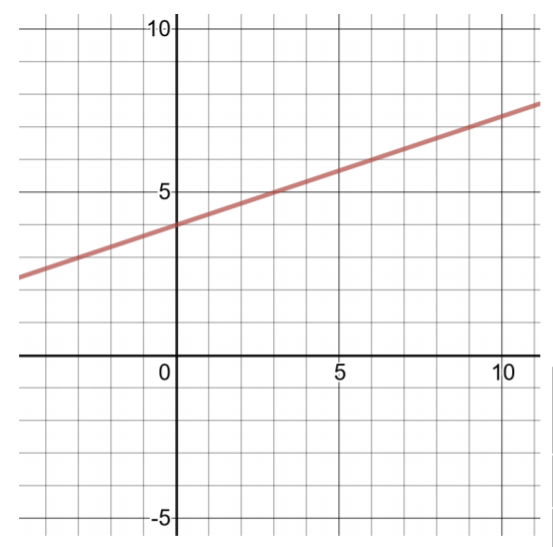
| 的解决方案表\(g(x) =\dfrac{ 1 }{3} x + 4\) | |
| \(x\) | \(g(x)\) |
| 0 | \(g(0) = \dfrac{1 }{3} (0) + 4 = 4\) |
| 3 | \(g(3) = \dfrac{1 }{3} (3) + 4 = 1 + 4 = 5\) |
创建解表并绘制以下线性函数的图形：
\(h(x) = −4x − 1\)
解决方案
要找到两个有序对，请选择小值\(x\)，然后计算值\(h(x)\)。
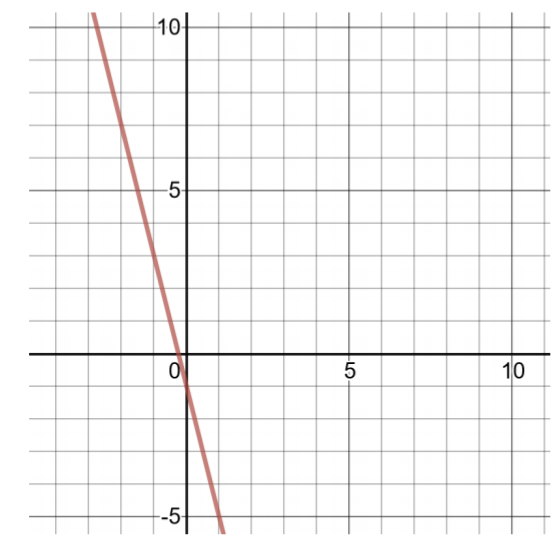
| 的解决方案表\(h(x) = −4x − 1\) | |
| \(x\) | \(h(x)\) |
| 0 | \(h(0) = −4(0) − 1 = −1\) |
| 1 | \(h(1) = −4(1) − 1 = −5\) |
创建解表并绘制以下线性函数的图形：
\(h(x) = − \dfrac{3 }{4} x − \dfrac{1 }{4}\)
解决方案
要找到两个有序对，请选择小值\(x\)，然后计算值\(h(x)\)。因为所含项的系数\(x\)是分数，所以选择分母的倍数\(− \dfrac{3}{4} x\)使乘积成为整数。
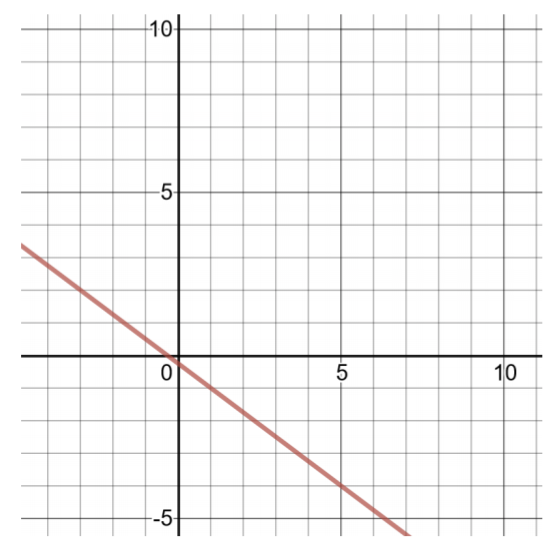
| 的解决方案表\(h(x) = − \dfrac{3}{4} x − \dfrac{1}{4}\) | |
| \(x\) | \(h(x)\) |
| 0 | \(h(0) = − \dfrac{3}{4} (0) − \dfrac{1}{4} = − \dfrac{1}{4}\) |
| 4 | \(h(4) = − \dfrac{3}{4} (4) − \dfrac{1}{4} = −3 − \dfrac{1}{4} = −3 \dfrac{1}{4}\) |
创建解表并绘制以下线性函数的图形：
- \(f(x) = 4x − 9\)
- \(g(x) = \dfrac{1}{ 2} x − 2\)
- \(h(x) = −3x + 5\)
- \(f(x) = − \dfrac{2}{ 3} x −\dfrac{ 1 }{3}\)