2.2: 有序对

Last updated

Oct 31, 2022
Page ID
171196
Save as PDF
- 2.1: 定义和标签象限
- 2.3: 距离公式

Victoria Dominguez, Cristian Martinez, & Sanaa Saykali
Citrus College via ASCCC Open Educational Resources Initiative

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

定义：有序对

有序对是用于在矩形坐标平面中定位点的数字对，其写形式为 $(x, y)$ ，其中 x 是 x 坐标，y 是 y 坐标。

有序对在象限中的位置将决定 x 和 y 坐标的符号，如上图上一节所示。因此，有序对的符号总结 $(x, y)$ 如下：

$(x, y)$ 如果在 Quadrant I 中，则 x 和 y 均为正数。
如果 $(x, y)$ 在象限 II 中，则 x 为负数，y 为正。
如果在 $(x, y)$ 象限 III 中，则 x 和 y 均为负数。
如果 $(x, y)$ 在象限 IV 中，则 x 为正，y 为负。

注意：矩形平面中垂直轴上的点不属于任何象限。

要在坐标平面中定位点，请使用一种称为绘制点图的过程。这个过程也可以称为绘制点。始终从原点开始，向右或向左移动以定位 x 坐标，向上或向下移动以定位 y 坐标。

要在坐标平面 $(−2, 5)$ 上绘制或绘图，请从原点开始，向左移动 2 个单位，因为 x 坐标 −2 为负，然后向上移动 5 个单位，因为 y 坐标 5 为正并画一个点。注意我们的点在象限 II 中。要绘制点图 $(4, 1)$ ，请从原点开始，向右移动 4 个单位，向上移动 1 个单位。同样，绘 $(−1, −1)$ 制点的图表 $(2, −3)$ ，如下图所示。

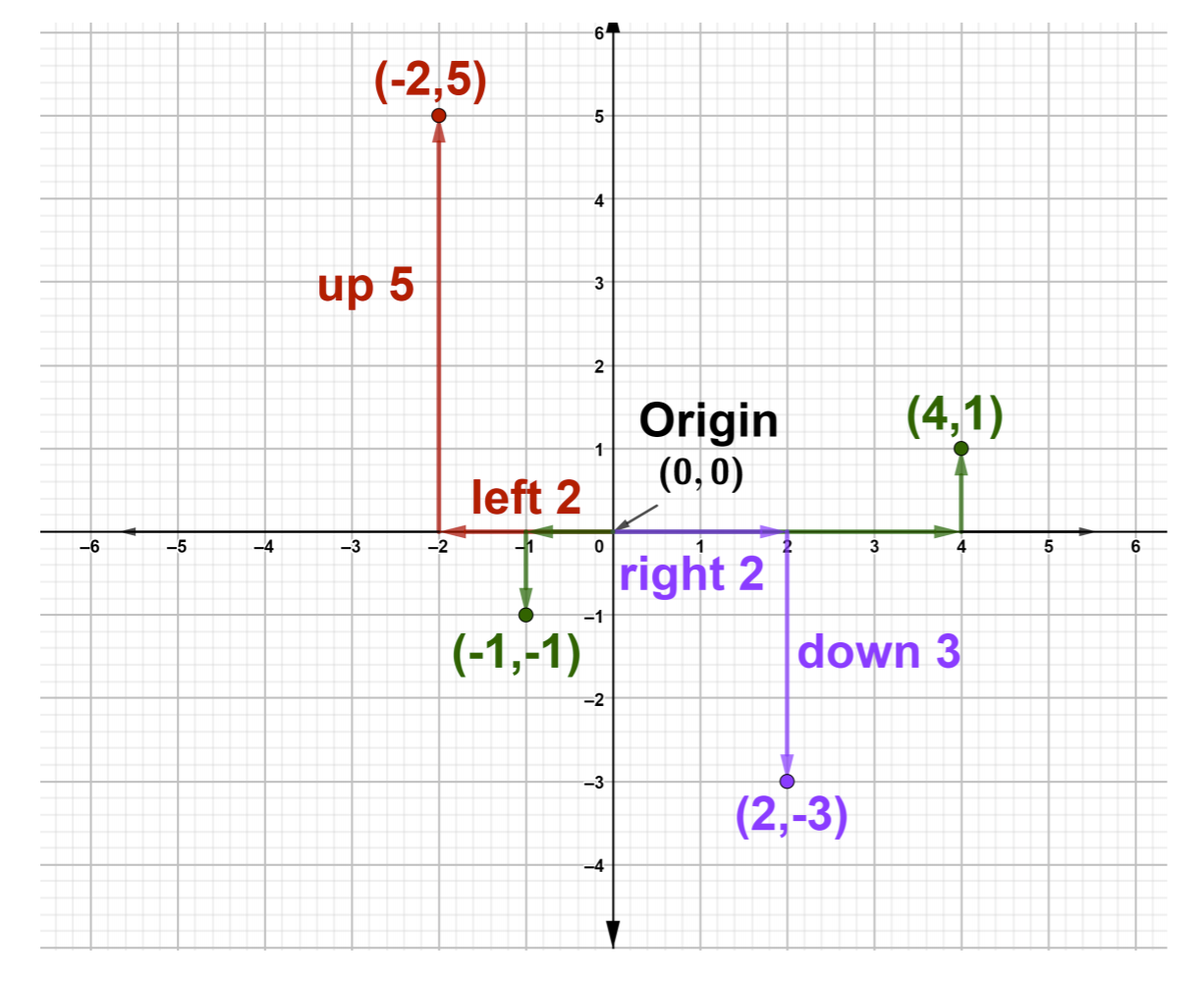
小心！ 在上一章中， $(p, q)$ 该表示法用于用区间表示法表示绝对值不等式解。本节介绍使用相同圆括号表示的有序对。确保不要将间隔符号与有序对表示法混淆。

示例 Template:Index

在同一个矩形坐标平面上绘制给定点的图形，并说明每个点的位置。如果一个点不在任何象限中，请说明它所在的轴。

$(3, 4)$
$(−2, −2)$
$\left(0, \dfrac{5 }{2 }\right)$
$(−3.5, 0)$

解决方案

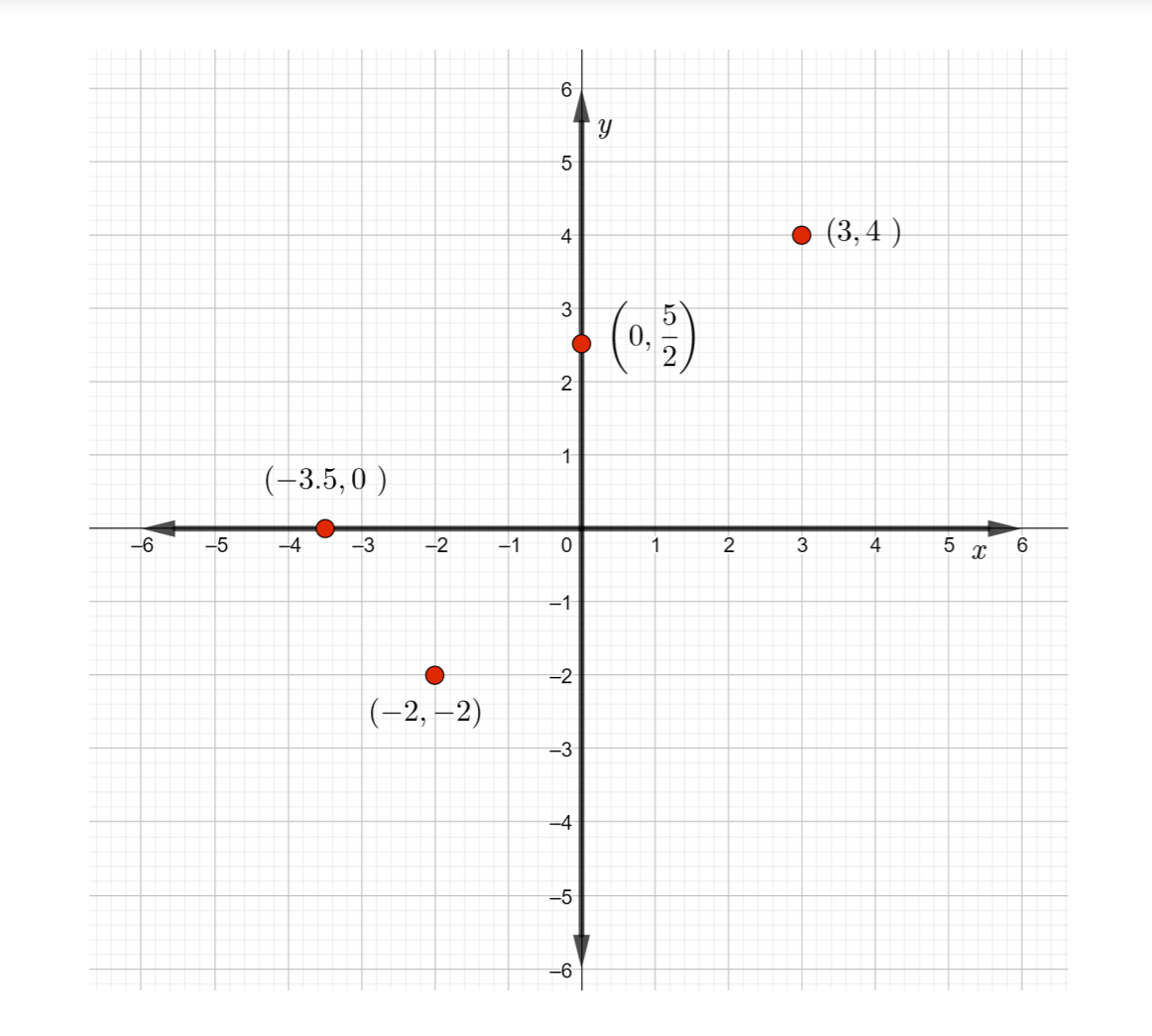
x 和 y 坐标均为正。从原点开始，然后向右移动 3 个单位，向上移动 4 个单位并标记 $(3, 4)$ 该点位于象限 I 中
x 和 y 坐标均为负值。从原点开始，向左移动 2 个单位，然后向下移动 2 个单位并标记该点 $(−2, −2)$ 。重点在于象限 II。
由于 x 坐标为 0，请从原点开始，不要向右或向左移动。由于 y 坐标为正，因此向上移动 $\dfrac{5 }{2}$ 单位或 2.5 个单位。标签点 $\left(0, \dfrac{5 }{2} \right)$ 。该点位于 y 轴上。
由于 x 坐标为负，从原点开始，向左移动 3.5 个单位。由于 y 坐标为 0，因此不要向上或向下移动。给点加上标签 $(−3.5, 0)$ 。该点位于 x 轴上。

示例 Template:Index

确定下图中标记的点的坐标。

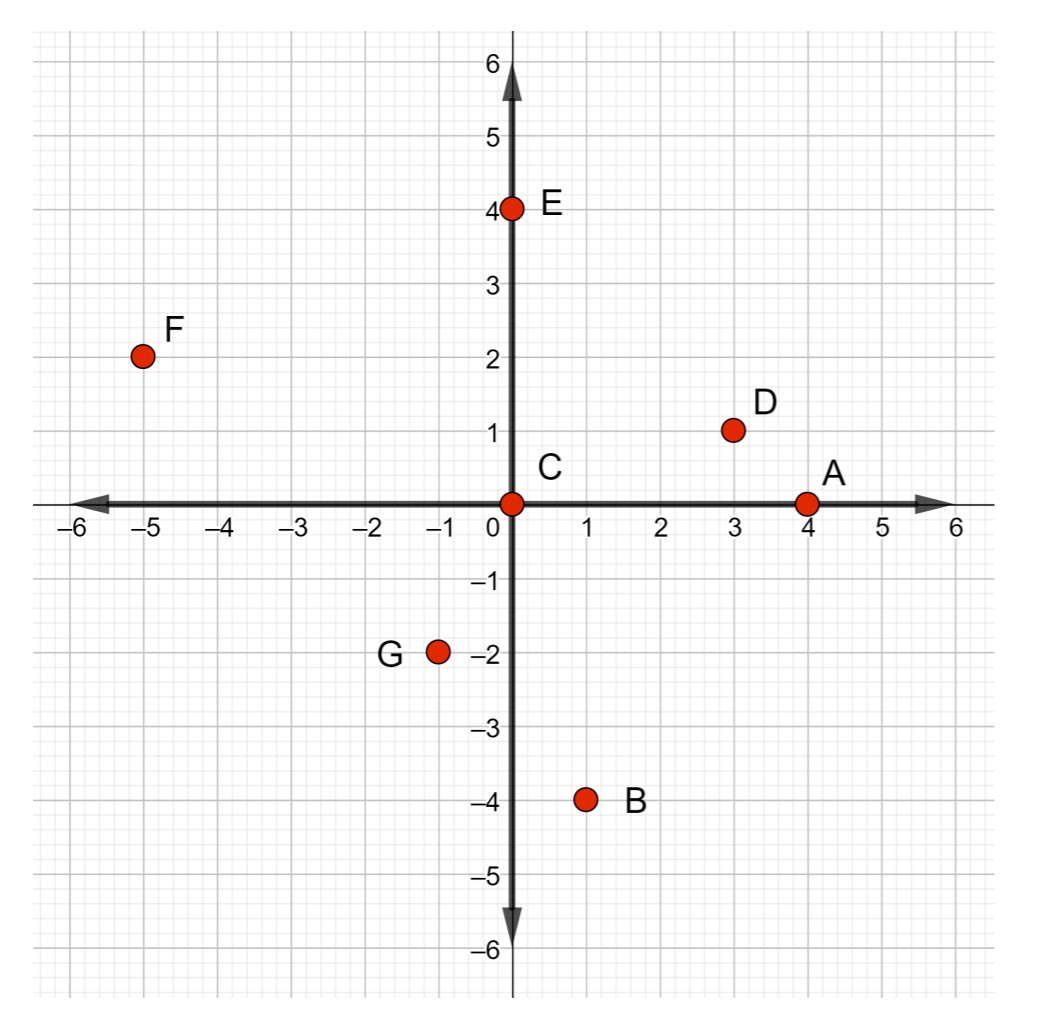
解决方案

要绘制坐标平面中的任何点，请从原点开始，然后根据给定坐标的符号移动，如下所示：

点 A：从原点开始，向右移动 4 个单位。 x 坐标为 4。没有向上或向下垂直移动，因此 y 坐标为 0。因此，点 A 有坐标 $(4, 0)$
B 点：再次从原点开始，向右移动 1 个单位，向下移动 4 个单位。因此，点 B 有坐标 $(1, −4)$
点 C：由于 x 坐标为 0，则从原点开始，不要向右或向左移动。 y 坐标也是 0，所以不要向上或向下移动。因此，点 C 的坐标是 $(0, 0)$
点 D：从原点向右移动 3 个单位，然后向上移动 1 个单位。因此，点 D 的坐标是 $(3, 1)$
点 E：由于 x 坐标为 0，从原点开始并停留在原点处，然后向上移动 4 个单位。因此，点 E 有坐标 $(0, 4)$ 。
点 F：从原点向左移动 5 个单位，向上移动 2 个单位。点 F 有坐标 $(−5, 2)$
点 G：从原点向左移动 1 个单位，向下移动 2 个单位。点 G 有坐标 $(−1, −2)$

练习 Template:Index

和中的 x 和 y 坐标是多 $(−3, 2)$ $(2, −3)$ 少？他们是一样的观点吗？
在同一个矩形坐标平面上绘制以下点，并说明每个点所在的象限或其所在的轴。 $(−1.5, 2),\quad (0, −3), \quad(5, 2.5),\quad \left(− \dfrac{1}{ 2 },\quad − \dfrac{1 }{2}\right), \quad\left(3\dfrac{1 }{2} ,\quad −\dfrac{ 7 }{2}\right ), \quad (−3, 3),\quad (−2, 0)$
确定下图中每个给定点的坐标。
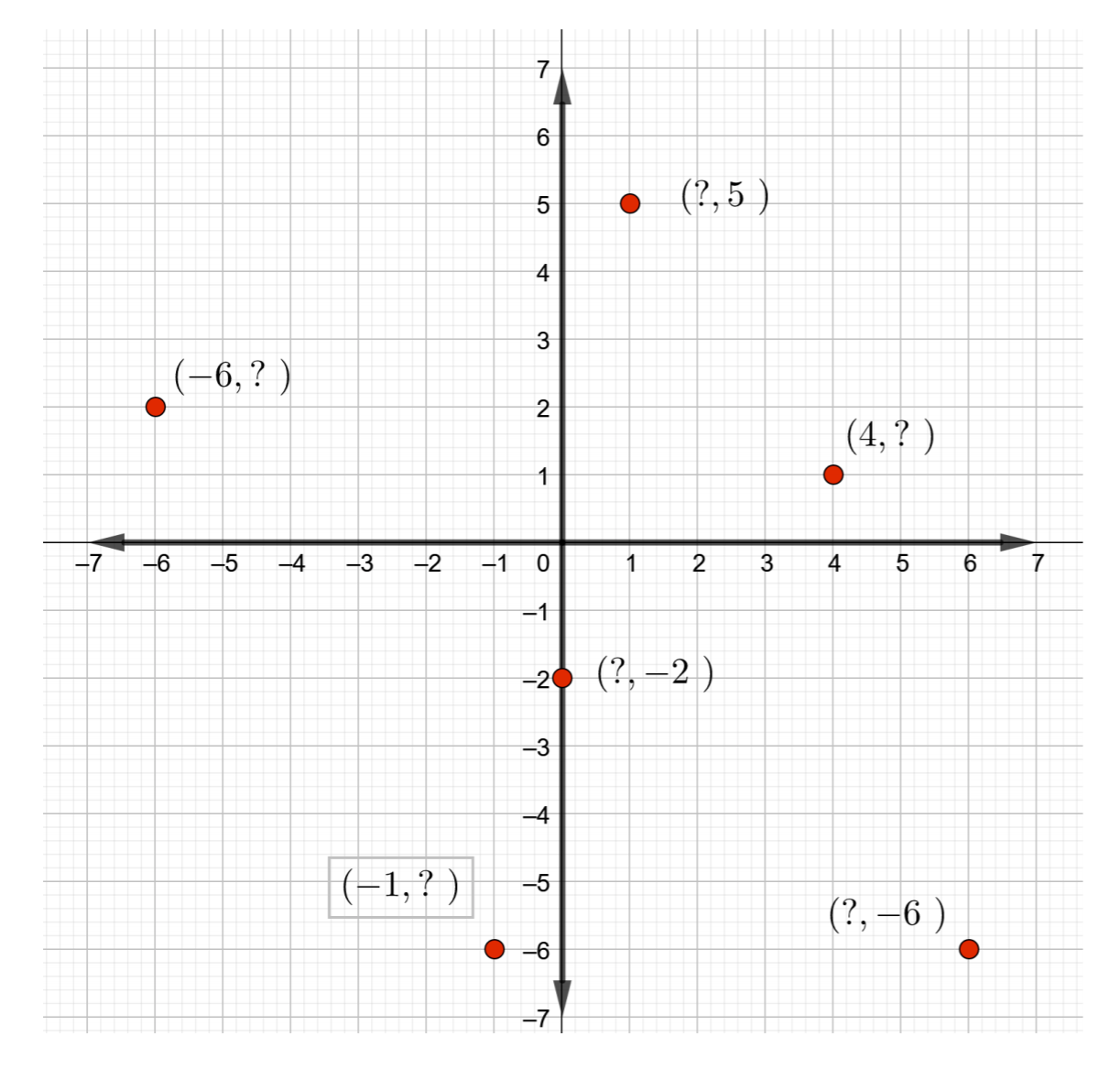
$clipboard_e1ef80ad5824aad92f10d741b80deac84.png$
图 Template:Index
确定下图中每个给定点的坐标。
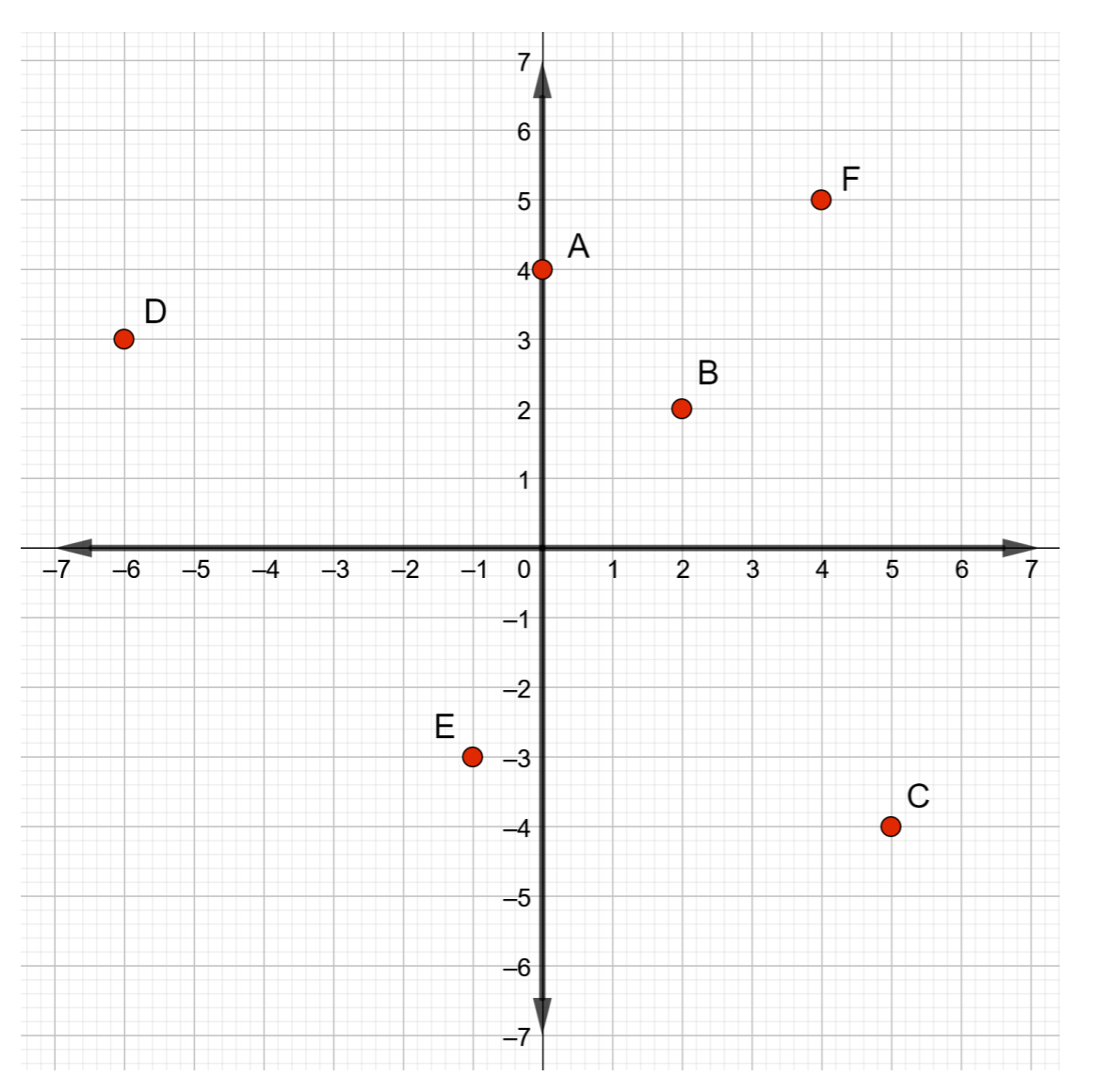
$clipboard_ef393b7a664660f0ac9517c9066d7f940.png$
图 Template:Index