2.1: 定义和标签象限
- Page ID
- 171195
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
矩形坐标系也称为笛卡尔坐标系,它以网格为基础,由两条垂直的数字线组成,水平数字线称为 x 轴,垂直数字线称为 y 轴。 矩形坐标系上的每个点都可以通过唯一的 x 和 y 坐标来识别。
两条垂直的数字线在该点处相交\((0, 0)\),被称为原点。 矩形坐标系分为四个区域。 这些区域被称为象限,用罗马数字标记,如下图所示:象限 I、象限 II、象限 III 和象限 IV,如下图所示
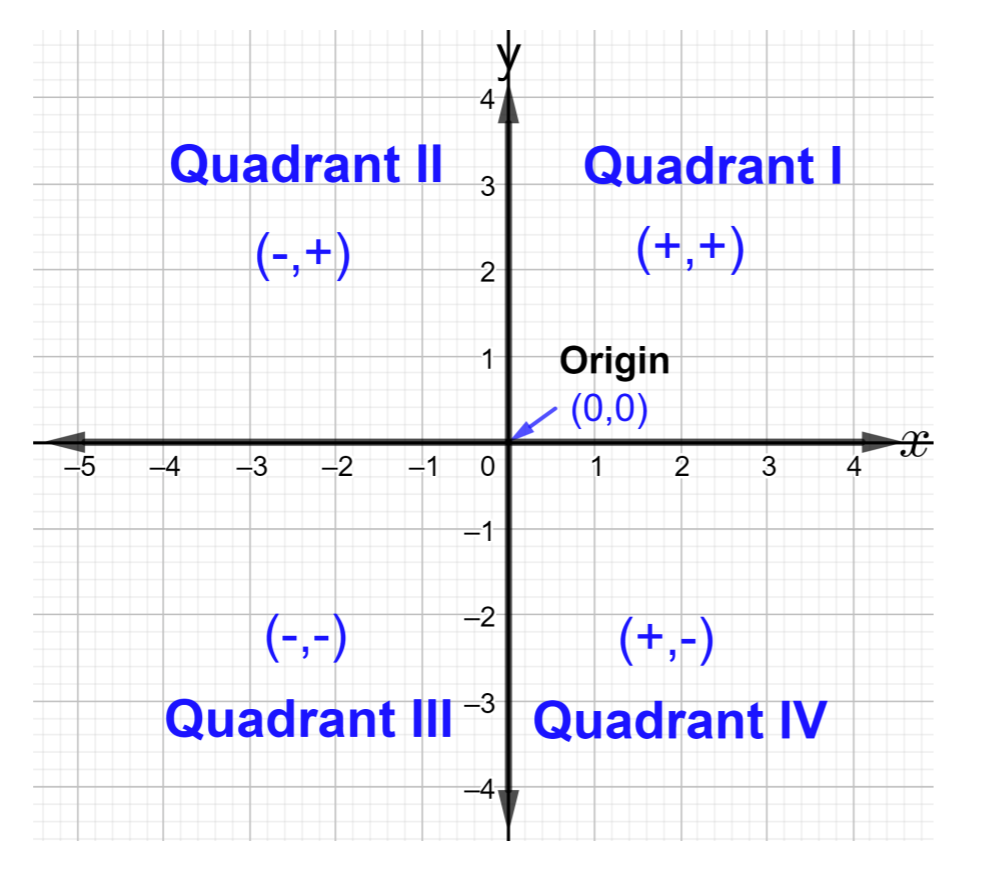
坐标平面中的每个点对应一个唯一的有序对\((x, y)\),其中\(x\)和\(y\)是任何实数。 有序对总是先有 x 坐标(左边),第二个是\(y\)-坐标(右边)。 \((6, 4)\)、\(\left(−.33, \dfrac{1}{5} \right)\)\((100, −2)\)、\(\left( \sqrt{ 3}, \dfrac{1 }{2}\right )\)是有序对的几个示例。 将有序对\((6, 4)\)读作 “点六,四”,其中 6 是\(x\)坐标,4 是\(y\)坐标。
- 这种形式叫什么积分\((x, y)\)?
- 确定以下有序对的坐标:\((−10, 0)\)、\((0.5, −6)\)、\(\left(\dfrac{1}{ 2} , −\dfrac{ 5 }{3} \right)\)
- 命名并说明矩形坐标系垂直轴相交点的有序对点。
- 陈述直角坐标系中的 4 个区域。
- 命名有序对中的第一个坐标。
- 命名有序对中的第二个坐标。
- 矩形坐标系中的水平数字线是什么?
- 矩形坐标系中的垂直数字线是什么?


