12.5: 二项式定理

Last updated
Save as PDF

Page ID: 203867

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

使用帕斯卡三角形扩展二项式
评估二项式系数
使用二项式定理扩展二项式

在开始之前，请参加这个准备测验。

简化：$\frac{7 \cdot 6 \cdot 5 \cdot 4}{4 \cdot 3 \cdot 2 \cdot 1}$。
如果你错过了这个问题，请查看示例 1.25。
扩展：$(3 x+5)^{2}$。
如果您错过了此问题，请查看示例 5.32。
扩展：$(x-y)^{2}$。
如果您错过了此问题，请查看示例 5.32。

使用帕斯卡三角形扩展二项式

在我们之前的工作中，我们使用FOIL或使用二项式方块图案对二项式进行了平方。我们也可以说我们扩大$(a+b)^{2}$了。

$(a+b)^{2}=a^{2}+2 a b+b^{2}$

为了扩大规模$(a+b)^{3}$，我们认识到这是事实，$(a+b)^{2}(a+b)$然后成倍增加。

$(a+b)^{3}$
$(a+b)^{2}(a+b)$
$\left(a^{2}+2 a b+b^{2}\right)(a+b)$
$a^{3}+2 a^{2} b+a b^{2}+a^{2} b+2 a b^{2}+b^{3}$
$a^{3}+3 a^{2} b+3 a b^{2}+b^{3}$
$(a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}$

为了找到一种不那么繁琐且适用于更高扩展的方法$(a+b)^{7}$，我们再次在一些扩展中寻找模式。

表 12.4.1
	术语数量	第一学期	最后一学期
$(a+b)^{1}=a+b$	$2$	$a^{1}$	$b^{1}$
$(a+b)^{2}=a^{2}+2 a b+b^{2}$	$3$	$a^{2}$	$b^{2}$
$(a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}$	$4$	$a^{3}$	$b^{3}$
$(a+b)^{4}=a^{4}+4 a^{3} b+6 a^{2} b^{2}+4 a b^{3}+b^{4}$	$5$	$a^{4}$	$b^{4}$
$(a+b)^{5}=a^{5}+5 a^{4} b+10 a^{3} b^{2}+10 a^{2} b^{3}+5 a b^{4}+b^{5}$	$6$	$a^{5}$	$b^{5}$
$(a+b)^{n}$	$n$	$a^{n}$	$b^{n}$

请注意，第一个和最后一个项仅显示一个变量。回想一下$a^{0}=1$，我们可以重写第一个和最后一个术语以包含这两个变量。例如，我们可以扩展$(a+b)^{3}$以显示带有两个变量的每个术语。

此图显示了模式 a 加 b 对 3 的幂等于 a 对 3 乘以 b 的幂次乘以 0 加上 3 倍 a 到 2 倍 b 的乘以 1 的幂加 3 a 到 0 乘以 b 的幂次方对 3 的幂次方。 — 图 12.4.1

通常，我们不显示零指数，就像我们平时写的那样，$x$而不是$1x$。

注意

扩张中的模式$(a+b)^{n}$

项数为$n+1$。
第一个学期是$a^{n}$，最后一个学期是$b^{n}$。
每个$a$项上的指数从左到右减一。
每个项的指数从左向右$b$增加 1。
任何项的指数之和为$n$。

让我们来看一个例子来突出最后三种模式。

此图显示了模式 a 加 b 乘以 5 的次方等于 a 加 5 倍 a 乘以 b 加 10 倍 a 乘以 b 加 5 倍 a 乘以 b。 — 图 12.4.2

从我们确定的模式中，我们可以看到扩展中的变量将是$(a+b)^{n}$

$(a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n}$。

为了找出各项的系数，我们再次以系数为重点编写扩展。我们将系数重写到右边，形成系数数组。

A 加 b 对 0 的幂等于 1。帕斯卡三角形的最高等级为 1。 A 加 b 对 1 的乘方等于 1 a 加 1 b。帕斯卡三角形的第二级是 1, 1。 A 加 b 对 2 的幂等于 1 a 加 2 的幂加 2 a b 加 1 b 对 2 的幂次方。帕斯卡三角形的第三层是 1、2、1。 A 加 b 对 3 的乘方等于 1 a 对 3 的乘方加 3 a 对 2 b 加 3 a 的幂加 3 a b 的乘以 2 加 1 b 对 3 的乘方。帕斯卡三角形的第四层是1,3,3,1。 A 加 b 对 4 的幂等于 1 a 乘以 4 的次方加 4 a 的次方加 3 b 加 6 a 对 2 b 的次方加 4 a 的次方加 3 的次方加 1 b 对 4 的次方。帕斯卡三角形的第五层是 1、4、6、4、1。 A 加 b 对 5 的幂等于 1 a 乘以 5 的次方加 5 a 的次方加 4 b 加 10 a 对 3 b 的次方加 2 的幂加 10 a 对 2 b 的次方对 3 的次方。帕斯卡三角形的第六行是 1、5、10、10、5、1。 — 图 12.4.3

右边的数组被称为帕斯卡三角形。请注意，数组中的每个数字都是上一行中最接近的两个数字的总和。我们可以通过以下方法找到下一行：以一个开头和结尾，然后将两个相邻的数字相加。

此图显示了帕斯卡的三角形。第一级是 1。第二级是 1、1。第三级是 1、2、1。第四级是 1、3、3、1。第五级是 1、4、6、4、1。第六级是 1、5、10、10、5、1。第七级是 1、6、15、20、15、6、1。 — 图 12.4.4

当我们展开二项式时，这个三角形给出了项的系数。

定义$\PageIndex{1}$

帕斯卡三角形

在下一个示例中，我们将使用这个三角形和我们识别的模式来扩展二项式。

示例$\PageIndex{1}$

使用帕斯卡三角形进行扩展$(x+y)^{6}$。

解决方案：

我们知道这次扩张的变量将遵循我们确定的模式。的非零指数$x$将从 6 开始，减小为 1。的非零指数$y$将从 1 开始，然后增加到 6。每个项中的指数之和将为六。按照我们的模式，$a=x$和$b=y$。

$\begin{array}{l}{(a+b)^{n}=a^{n}+\_\_\_a^{n-1} b^{1}+\_\_\_a^{n-2} b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n}} \\ {(x+y)^{6}=x^{6}+\_\_\_x^{5} y^{1}+\_\_\_x^{4} y^{2}+\_\_\_x^{3} y^{3}+\_\_\_x^{2} y^{4}+\_\_\_x^{1} y^{5}+y^{6}}\end{array}$

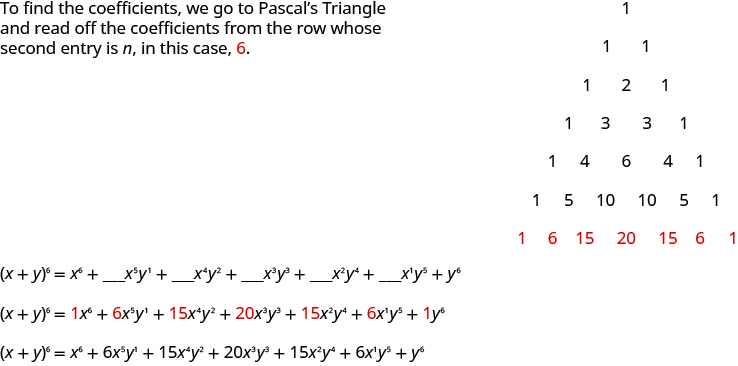
此图显示 n 减去 1 b 的次方加 a 对 n 的幂加 a 的次方，如果 n 减去 1 b 乘以 n 的次方加 a 对 n 的次方减去 2 b 的次方，如果 2 加省略号加 a 对 1 b 的次方减 n 的幂减 1 加 b 的次方。下图显示 x 加 y 的次方6 的 x 等于 6 加 x 的次方乘以 5 y 的次方乘以 1 加 x 到 4 y 的次方乘以 2 加 x 的次方到 3 y 的幂到 3 加 x 的次方到 2 y 的次方到 4 加 x 的次方再到 1 y 的次方乘以 5 加 y 对 6 的次方。 — 图 12.4.6

练习$\PageIndex{1}$

使用帕斯卡三角形进行扩展$(x+y)^{5}$。

回答: $\begin{array}{l}{x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}} {+5 x y^{4}+y^{5}}\end{array}$

练习$\PageIndex{2}$

使用帕斯卡三角形进行扩展$(p+q)^{7}$。

回答: $\begin{array}{c}{p^{7}+7 p^{6} q+21 p^{5} q^{2}+35 p^{4} q^{3}} {+35 p^{3} q^{4}+21 p^{2} q^{5}+7 p q^{6}+q^{7}}\end{array}$

在下一个例子中，我们想用一个变量和一个常量来扩展二项式。我们需要识别$a$并$b$仔细应用该模式。

示例$\PageIndex{2}$

使用帕斯卡三角形进行扩展$(x+3)^{5}$。

解决方案：

我们确定图案$b$的$a$和。

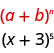
此图显示了我们如何在 x 加 3 到 5 的幂次方中识别 a 加 b 的 n 次方。 — 图 12.4.7

按照我们的模式，$a=x$和$b=3$。

我们知道这次扩张的变量将遵循我们确定的模式。每个项中的指数之和将为五。

$(a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n} $

$(x+3)^{5}=x^{5}+\_\_\_x^{4}\cdot3^{1}+\_\_\_x^{3}\cdot3^{2}+\_\_\_x^{2}\cdot3^{3}+\_\_\_x^{1}\cdot3^{4}+3^{5}$

此图显示了帕斯卡的三角形。第一级是 1。第二级是 1、1。第三级是 1、2、1。第四级是 1、3、3、1。第五级是 1、4、6、4、1。第六级是 1、5、10、10、5、1。第七级是 1、6、15、20、15、6、1。此图显示 X 加 3 乘以 5 的幂等于 1 x 乘以 5 g 3 x 到 4 的次方加 10 g 9 x 到 3 的次方加 10 g 27 x 的次方加 2 加 5 g 81 x 的次方乘以 1 加 1 g 243 的次方。然后，x 加 3 对 5 的幂等于 x 乘以 5 的乘方加 15 x 到 4 的乘方加 90 x 到 3 加 270 x 再加 2 加 405 加 243 的次方。 — 图 12.4.8

练习$\PageIndex{3}$

使用帕斯卡三角形进行扩展$(x+2)^{4}$。

回答: $x^{4}+8 x^{3}+24 x^{2}+32 x+16$

练习$\PageIndex{4}$

使用帕斯卡三角形进行扩展$(x+1)^{6}$。

回答: $\begin{array}{l}{x^{6}+6 x^{5}+15 x^{4}+20 x^{3}+15 x^{2}} {+6 x+1}\end{array}$

在下一个示例中，二项式是差值，第一个项的常数乘以变量。一旦我们确定了图案$b$的$a$和，就必须再次仔细应用该图案。

示例$\PageIndex{3}$

使用帕斯卡三角形进行扩展$(3x-2)^{4}$。

解决方案：

我们确定图案$b$的$a$和。

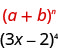
此图显示了我们如何在 3 x 减 2 到 4 的幂次方中识别出 a 加 b 的 n 次方。 — 图 12.4.9

按照我们的模式，$a=3x$和$b=-2$。

$(a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n} $

$(3 x-2 )^{4}=1 \cdot\left(\stackrel{3}{x}+4(3 x)^{3}(-2)^{1}+6(3 x)^{2}(-2)^{2}+4(3 x)^{1}(-2)^{3}+1 \cdot(-2)^{4}\right.$

$(3 x-2)^{4}=81 x^{4}+4\left(27 x^{3}\right)(-2)+6\left(9 x^{2}\right)(4)+4(3 x)(-8)+1 \cdot 16$

$(3 x-2 )^{4}=81 x^{4}-216 x^{3}+216 x^{2}-96 x+16$

练习$\PageIndex{5}$

使用帕斯卡三角形进行扩展$(2x-3)^{4}$。

回答: $16 x^{4}-96 x^{3}+216 x^{2}-216 x+81$

练习$\PageIndex{6}$

使用帕斯卡三角形进行扩展$(2x-1)^{6}$。

回答: $\begin{array}{l}{64 x^{6}-192 x^{5}+240 x^{4}-160 x^{3}} {+60 x^{2}-12 x+1}\end{array}$

评估二项式系数

虽然帕斯卡三角形是扩展二项式的一种方法，但我们还将研究另一种方法。在我们开始讨论这个问题之前，我们需要引入一些更多的阶乘表示法。这种表示法不仅用于扩展二项式，还用于概率的研究和使用。

要找到扩展二项式项的系数，我们需要能够评估称为二项式系数的表示法$\left( \begin{array}{l}{n} \\ {r}\end{array}\right)$。我们读$\left( \begin{array}{l}{n} \\ {r}\end{array}\right)$作 “$n$选择$r$” 或 “$r$一次$n$拍摄”。

定义$\PageIndex{1}$

二项式系数$\left( \begin{array}{l}{n} \\ {r}\end{array}\right)$，其中$r$和$b$是整数$0 \leq r \leq n$，定义为

$\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}$

我们读$\left( \begin{array}{l}{n} \\ {r}\end{array}\right)$作 “$n$选择$r$” 或 “$r$一次$n$拍摄”。

示例$\PageIndex{4}$

评估：

$\left( \begin{array}{l}{5} \\ {1}\end{array}\right)$
$\left( \begin{array}{l}{7} \\ {7}\end{array}\right)$
$\left( \begin{array}{l}{4} \\ {0}\end{array}\right)$
$\left( \begin{array}{l}{8} \\ {5}\end{array}\right)$

解决方案：

a. 我们将使用二项式系数的定义，

$\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}$

$\left( \begin{array}{l}{5} \\ {1}\end{array}\right)$

使用定义$\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}$，在哪里$n=5, r=1$。

$\frac{5 !}{1 !(5-1) !}$

简化。

$\frac{5 !}{1 !(4) !}$

重写$5!$为$5\cdot 4!$

$\frac{5 \cdot 4 !}{1 ! \cdot 4 !}$

通过删除常见因素来简化。

$\frac{5\cdot \cancel{4 !}}{1 ! \cdot \cancel{4 !}}$

简化。

$5$

$\left( \begin{array}{l}{5} \\ {1}\end{array}\right)=5$

b。$\left( \begin{array}{l}{7} \\ {7}\end{array}\right)$

使用定义$\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}$，在哪里$n=7, r=7$。

$\frac{7 !}{7 !(7-7) !}$

简化。

$\frac{7 !}{7 !(0) !}$

简化。记住$0!=1$。

$1$

$\left( \begin{array}{l}{7} \\ {7}\end{array}\right)=1$

c。$\left( \begin{array}{l}{4} \\ {0}\end{array}\right)$

使用定义$\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}$，在哪里$n=4, r=0$。

$\frac{4 !}{0 !(4-0) !}$

简化。

$\frac{4 !}{0 !(4) !}$

简化。

$1$

$\left( \begin{array}{l}{4} \\ {0}\end{array}\right)=1$

d。$\left( \begin{array}{l}{8} \\ {5}\end{array}\right)$

使用定义$\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}$，在哪里$n=8, r=5$。

$\frac{8 !}{5 !(8-5) !}$

简化。

$\frac{8 !}{5 !(3) !}$

重写$8!$为$8\cdot 7\cdot 6\cdot 5!$并删除常见因素。

$\frac{8\cdot7\cdot\cancel{6}\cdot\cancel{5!}}{\cancel{5!}\cdot\cancel{3}\cdot\cancel{2}\cdot1}$

简化。

$56$

$\left( \begin{array}{l}{8} \\ {5}\end{array}\right)=56$

练习$\PageIndex{7}$

评估每个二项式系数：

$\left( \begin{array}{l}{6} \\ {1}\end{array}\right)$
$\left( \begin{array}{l}{8} \\ {8}\end{array}\right)$
$\left( \begin{array}{l}{5} \\ {0}\end{array}\right)$
$\left( \begin{array}{l}{7} \\ {3}\end{array}\right)$

回答

$6$
$1$
$1$
$35$

练习$\PageIndex{8}$

评估每个二项式系数：

$\left( \begin{array}{l}{2} \\ {1}\end{array}\right)$
$\left( \begin{array}{l}{11} \\ {11}\end{array}\right)$
$\left( \begin{array}{l}{9} \\ {0}\end{array}\right)$
$\left( \begin{array}{l}{6} \\ {5}\end{array}\right)$

回答

$2$
$1$
$1$
$6$

在前面的示例中$(a)$，$(b)$，$(c)$演示了二项式系数的一些特殊属性。

定义$\PageIndex{2}$

二项式系数的性质

$\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1$

使用二项式定理扩展二项式

我们现在准备使用扩展二项式的替代方法了。 二项式定理对变量使用相同的模式，但使用二项式系数作为每个项的系数。

定义$\PageIndex{3}$

二项式定理

对于任何实数$a$和$b$正整数$n$，

$(a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}$

示例$\PageIndex{5}$

使用二项式定理进行扩展$(p+q)^{4}$。

解决方案：

我们确定图案$b$的$a$和。

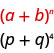
此图显示了我们如何将 a 加 b 与 n 的幂相提并论，其模式为 p 加 q 到 4 的幂次方。 — 图 12.4.11

按照我们的模式，$a=p$和$b=q$。

我们使用二项式定理。

在值中替换$a=p, b=q$和$n=4$。

$(p+q)^{4}=\left( \begin{array}{c}{4} \\ {0}\end{array}\right) p^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right) p^{4-1} q^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right) p^{4-2} q^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right) p^{4-3} q^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) q^{4}$

简化指数。

$(p+q)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right) p^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right) p^{3} q+\left( \begin{array}{c}{4} \\ {2}\end{array}\right) p^{2} q^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right) p q^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) q^{4}$

评估系数，记住，$\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1$

$(p+q)^{4}=1 p^{4}+4 p^{3} q^{1}+\frac{4 !}{2 !(2) !} p^{2} q^{2}+\frac{4 !}{3 !(4-3) !} p^{1} q^{3}+1 q^{4}$
$(p+q)^{4}=p^{4}+4 p^{3} q+6 p^{2} q^{2}+4 p q^{3}+q^{4}$

练习$\PageIndex{9}$

使用二项式定理进行扩展$(x+y)^{5}$。

回答: $\begin{array}{l}{x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}} {+5 x y^{4}+y^{5}}\end{array}$

练习$\PageIndex{10}$

使用二项式定理进行扩展$(m+n)^{6}$。

回答: $\begin{array}{l}{m^{6}+6 m^{5} n+15 m^{4} n^{2}+20 m^{3} n^{3}} {+15 m^{2} n^{4}+6 m n^{5}+n^{6}}\end{array}$

请注意，当我们在上一个示例$(p+q)^{4}$中使用二项式定理进行扩展时，我们得到的系数与使用帕斯卡三角形获得的系数相同。

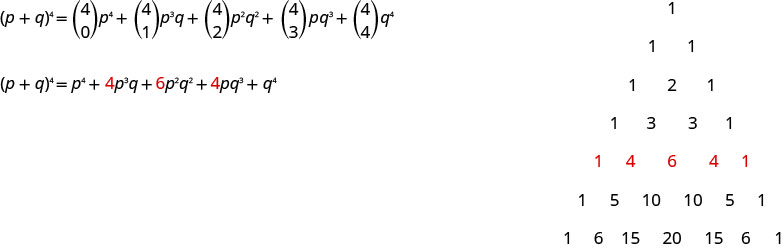
上图是 P 加 q 对 4 的次方等于 4 选择 0 倍 p 到 4 的幂次方选择 1 倍 p 为 3 q 加 4 的次方选择 2 倍 p 到 2 q 的次方选择 3 倍 p q 到 3 加 4 的次方选择 4 的幂次方。 P 加 q 对 4 的幂等于 p 乘以 3 q 加 6 p 的次方乘以 2 q 的次方加 2 q 的次方加 4 p q 的次方加 3 加 q 的次方加 4 的次方。右边的这个图显示了帕斯卡的三角形。第一级是 1。第二级是 1、1。第三级是 1、2、1。第四级是 1、3、3、1。第五级是 1、4、6、4、1。第六级是 1、5、10、10、5、1。第七级是 1、6、15、20、15、6、1。 — 图 12.4.12

下一个例子，二项式是区别。当二项式是差异时，我们必须谨慎识别我们将在模式中使用的值。

示例$\PageIndex{6}$

使用二项式定理进行扩展$(x-2)^{5}$。

解决方案：

我们确定图案$b$的$a$和。

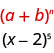
按照我们的模式，$a=x$和$b=-2$。

我们使用二项式定理。

在值中替换$a=x, b=-2$，和$n=5$。

$(x-2)^{5}=\left( \begin{array}{l}{5} \\ {0}\end{array}\right) x^{5}+\left( \begin{array}{c}{5} \\ {1}\end{array}\right) x^{5-1}(-2)^{1}+\left( \begin{array}{c}{5} \\ {2}\end{array}\right) x^{5-2}(-2)^{2}+\left( \begin{array}{c}{5} \\ {3}\end{array}\right) x^{5-3}(-2)^{3}+\left( \begin{array}{c}{5} \\ {4}\end{array}\right) x^{5-4}(-2)^{4}+\left( \begin{array}{c}{5} \\ {5}\end{array}\right)(-2)^{5}$

简化系数。记住，$\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1$。

$(x-2)^{5}=\left( \begin{array}{l}{5} \\ {0}\end{array}\right) x^{5}+\left( \begin{array}{c}{5} \\ {1}\end{array}\right) x^{4}(-2)+\left( \begin{array}{c}{5} \\ {2}\end{array}\right) x^{3}(-2)^{2}+\left( \begin{array}{c}{5} \\ {3}\end{array}\right) x^{2}(-2)^{3}+\left( \begin{array}{c}{5} \\ {4}\end{array}\right) x(-2)^{4}+\left( \begin{array}{c}{5} \\ {5}\end{array}\right)(-2)^{5}$

$(x-2)^{5}=1 x^{5}+5(-2) x^{4}+\frac{5 !}{2 ! \cdot 3 !}(-2)^{2} x^{3}+\frac{5 !}{3 ! 2 !}(-2)^{3} x^{2}+\frac{5 !}{4 !1 !}(-2)^{4} x+1(-2)^{5}$

$(x-2)^{5}=x^{5}+5(-2) x^{4}+10 \cdot 4 \cdot x^{3}+10(-8) x^{2}+5 \cdot 16 \cdot x+1(-32)$

$(x-2)^{5}=x^{5}-10 x^{4}+40 x^{3}-80 x^{2}+80 x-32$

练习$\PageIndex{11}$

使用二项式定理进行扩展$(x-3)^{5}$。

回答: $\begin{array}{l}{x^{5}-15 x^{4}+90 x^{3}-270 x^{2}} {+405 x-243}\end{array}$

练习$\PageIndex{12}$

使用二项式定理进行扩展$(y-1)^{6}$。

回答: $\begin{array}{l}{y^{6}-6 y^{5}+15 y^{4}-20 y^{3}+15 y^{2}} {-6 y+1}\end{array}$

当两个项都有系数和变量时，事情可能会变得混乱。

示例$\PageIndex{7}$

使用二项式定理进行扩展$(2x-3y)^{4}$。

解决方案：

我们确定图案$b$的$a$和。

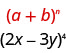
此图显示了我们如何将 a 加 b 与 n 的幂次方相提并论，模式为 2 x 减去 3 y 乘以 4 的幂次方。 — 图 12.4.14

按照我们的模式，$a=2x$和$b=-3y$。

我们使用二项式定理。

在值中替换$a=2x, b=-3y$和$n=4$。

$(2 x-3 y)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right)(2 x)^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right)(2 x)^{4-1}(-3 y)^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right)(2 x)^{4-2}(-3 y)^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right)(2 x)^{4-3}(-3 y)^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) (-3y)^{4}$

简化指数。

$(2 x-3 y)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right)(2 x)^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right)(2 x)^{3}(-3 y)^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right)(2 x)^{2}(-3 y)^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right)(2 x)^{1}(-3 y)^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right)(-3 y)^{4}$

评估系数。记住，$\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1$

$(2 x-3 y)^{4}=1(2 x)^{4}+4(2 x)^{3}(-3 y)^{1}+\frac{4 !}{2 !(2 x) !}(2 x)^{2}+\frac{4 !}{3 !(4-3) !}(2 x)^{3}(-3 y)^{3}+1(-3 y)^{4}$

$(2 x-3 y)^{4}=16 x^{4}+4 \cdot 8 x^{3}(-3 y)+6\left(4 x^{2}\right)\left(9 y^{2}\right)+4(2 x)\left(-27 y^{3}\right)+81 y^{4}$

$(2 x-3 y)^{4}=16 x^{4}-96 x^{3} y+216 x^{2} y^{2}-216 x y^{3}+81 y^{4}$

练习$\PageIndex{13}$

使用二项式定理进行扩展$(3x-2y)^{5}$。

回答: $\begin{array}{l}{243 x^{5}-810 x^{4} y+1080 x^{3} y^{2}} {-720 x^{2} y^{3}+240 x y^{4}-32 y^{5}}\end{array}$

练习$\PageIndex{14}$

使用二项式定理进行扩展$(4x-3y)^{4}$。

回答: $\begin{array}{l}{256 x^{4}-768 x^{3} y+864 x^{2} y^{2}} {-432 x y^{3}+81 y^{4}}\end{array}$

二项式定理的真正美妙之处在于，它为任何特定的扩展项提供了公式，而无需计算总和。让我们来看看二项式定理中的模式。

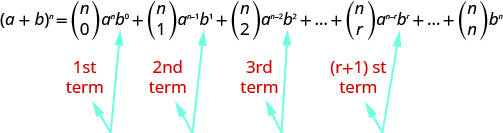
此图显示 a 加 b 对 n 的乘方等于 n 选择 0 乘以 a 乘以 n 的次方加 n 的次方加 n 选择 1 倍 a 给 n 的次方减去 1 b 再加 n 选择 2 倍 a 到 n 的幂减去 2 b 再加上省略号加 n 选择 r 乘以 n 减去 r 加的次方省略号加 n 选择 n 乘以 b 的 n 次方。 — 图 12.4.15

注意，在每种情况下，上的指数$b$都比项的数字小一。该$(r+1)^{st}$项是指其指数$b$为的项$r$。因此，我们可以使用$(r+1)^{st}$术语的格式来查找特定术语的值。

注意

在二项式扩展中找到特定术语

扩展中的$(r+1)^{s t}$术语$(a+b)^{n}$是

$\left( \begin{array}{l}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}$

示例$\PageIndex{8}$

找到第四个学期$(x+y)^{7}$.

解决方案：

表 12.4.1
按照我们的模式，$n=7, a=x$和$b=y$。	$。$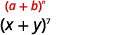
我们正在寻找第四个学期。从$r+1=4$那以后$r=3$。
写下公式	$。$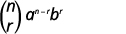
在值$n=7, r=3, a=x$、和中替换$b=y$。	$。$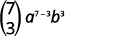
$。$	$。$
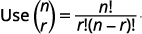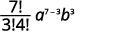简化。	$。$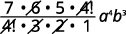
简化。	$。$

练习$\PageIndex{15}$

找到第三个学期$(x+y)^{6}$.

回答: $15x^{4}y^{2}$

练习$\PageIndex{16}$

找出第五个学期$(a+b)^{8}$.

回答: $8ab^{7}$

示例$\PageIndex{9}$

求$x^{6}$项的系数$(x+3)^{9}$。

解决方案：

表 12.4.2
那么，按照我们的模式$n=9, a=x$，和$b=3$。	$。$ 图 12.4.23
我们正在寻找该$x^{6}$项的系数。从那以后$a=x$$x^{9-r}=x^{6}$，我们知道$r=3$了。
写下公式。	$。$ 图 12.4.24
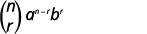
在值$n=9, 4=3, a=x$、和中替换$b=3$。	$。$ 图 12.4.25
$。$ 图 12.4.26	$。$ 图 12.4.27
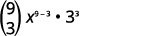
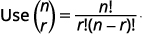
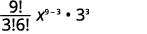
简化。	$。$ 图 12.4.28
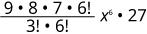
简化。	$。$ 图 12.4.29
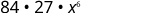
简化。	$。$ 图 12.4.30

练习$\PageIndex{17}$

求$x^{5}$项的系数$(x+4)^{8}$。

回答: $7,168$

练习$\PageIndex{18}$

求$x^{4}$项的系数$(x+2)^{7}$。

回答: $280$

访问这些在线资源以获取更多指导和序列练习。

关键概念

\ (a+b) ^ {n}\ (扩展中的模式
- 项数为$n+1$。
- 第一个学期是$a^{n}$，最后一个学期是$b^{n}$。
- 每个$a$项上的指数从左到右减一。
- 每个项的指数从左向右$b$增加 1。
- 任何项的指数之和为$n$。
帕斯卡三角形

二项式系数 $\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)$：二项式系数$\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)$，其中$r$和$n$是整数$0≤r≤n$，定义为

$\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}$

我们读$\left( \begin{array}{l}{n} \\ {r}\end{array}\right)$作 “$n$选择$r$” 或 “$r$一次$n$拍摄”。

二项式系数的性质

$\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1$

二项式定理：

对于任何实数$a$$b$、和正整数$n$，

	术语数量	第一学期	最后一学期
\((a+b)^{1}=a+b\)	\(2\)	\(a^{1}\)	\(b^{1}\)
\((a+b)^{2}=a^{2}+2 a b+b^{2}\)	\(3\)	\(a^{2}\)	\(b^{2}\)
\((a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\)	\(4\)	\(a^{3}\)	\(b^{3}\)
\((a+b)^{4}=a^{4}+4 a^{3} b+6 a^{2} b^{2}+4 a b^{3}+b^{4}\)	\(5\)	\(a^{4}\)	\(b^{4}\)
\((a+b)^{5}=a^{5}+5 a^{4} b+10 a^{3} b^{2}+10 a^{2} b^{3}+5 a b^{4}+b^{5}\)	\(6\)	\(a^{5}\)	\(b^{5}\)
\((a+b)^{n}\)	\(n\)	\(a^{n}\)	\(b^{n}\)

注意

定义\(\PageIndex{1}\)

示例\(\PageIndex{1}\)

练习\(\PageIndex{1}\)

练习\(\PageIndex{2}\)

示例\(\PageIndex{2}\)

练习\(\PageIndex{3}\)

练习\(\PageIndex{4}\)

示例\(\PageIndex{3}\)

练习\(\PageIndex{5}\)

练习\(\PageIndex{6}\)

定义\(\PageIndex{1}\)

示例\(\PageIndex{4}\)

练习\(\PageIndex{7}\)

练习\(\PageIndex{8}\)

定义\(\PageIndex{2}\)

定义\(\PageIndex{3}\)

示例\(\PageIndex{5}\)

练习\(\PageIndex{9}\)

练习\(\PageIndex{10}\)

示例\(\PageIndex{6}\)

练习\(\PageIndex{11}\)

练习\(\PageIndex{12}\)

示例\(\PageIndex{7}\)

练习\(\PageIndex{13}\)

练习\(\PageIndex{14}\)

注意

示例\(\PageIndex{8}\)

练习\(\PageIndex{15}\)

练习\(\PageIndex{16}\)

示例\(\PageIndex{9}\)

练习\(\PageIndex{17}\)

练习\(\PageIndex{18}\)

按照我们的模式，\(n=7, a=x\)和\(b=y\)。	$。$
我们正在寻找第四个学期。从\(r+1=4\)那以后\(r=3\)。
写下公式	$。$
在值\(n=7, r=3, a=x\)、和中替换\(b=y\)。	$。$
$。$	$。$
简化。	$。$
简化。	$。$

那么，按照我们的模式\(n=9, a=x\)，和\(b=3\)。	$。$ 图 12.4.23
我们正在寻找该\(x^{6}\)项的系数。从那以后\(a=x\)\(x^{9-r}=x^{6}\)，我们知道\(r=3\)了。
写下公式。	$。$ 图 12.4.24
在值\(n=9, 4=3, a=x\)、和中替换\(b=3\)。	$。$ 图 12.4.25
$。$ 图 12.4.26	$。$ 图 12.4.27
简化。	$。$ 图 12.4.28
简化。	$。$ 图 12.4.29
简化。	$。$ 图 12.4.30