12.2: 序列
- Page ID
- 203855
在本节结束时,您将能够:
- 写出序列的前几个项
- 找到序列的通用项(第 n 项)的公式
- 使用阶乘表示法
- 找出部分总和
- 使用求和表示法写出总和
在开始之前,请参加这个准备测验。
- 计算\(2n+3\)整数\(1, 2, 3\),然后\(4\)。
如果您错过了此问题,请查看示例 1.6。 - 计算\((−1)^{n}\)整数\(1, 2, 3\),然后\(4\)。
如果你错过了这个问题,请查看示例 1.19。 - 如果\(f(n)=n^{2}+2\),找到\(f(1)+f(2)+f(3)\)。
如果你错过了这个问题,请查看示例 3.49。
写出序列的前几个项
让我们来看看这个函数,\(f(x)=2x\)并仅根据计数数字对其进行评估。
| \(f(x)=2x\) | |
| \(x\) | \(2x\) |
| \(1\) | \(2\) |
| \(2\) | \(4\) |
| \(3\) | \(6\) |
| \(4\) | \(8\) |
| \(5\) | \(10\) |
| \(...\) | \(...\) |
如果我们按顺序列出函数值,然后\(2, 4, 6, 8\)\(10\),... 我们就有一个序列了。 序列是一个函数,其域是计数数字。
序列是一个函数,其域是计数数字。
序列也可以看作是有序的数字列表,列表中的每个数字都是一个术语。 一个序列可以有无限数量的项或有限数量的项。 我们的序列末尾有三个点(省略号),表示列表永无止境。 如果域是所有计数数字的集合,则该序列是无限序列。 它的域都是计数数字,并且有无限数量的计数数字。
\(2,4,6,8,10, \dots\)
如果我们将域限制为有限数量的计数数,则该序列是有限序列。 如果我们只使用前四个计数数字,\(1, 2, 3, 4\)我们的序列就是有限序列,
\(2,4,6,8\)
通常,在处理序列时,我们不想写出所有术语。 我们希望以更紧凑的方式来显示每个术语是如何定义的。 当我们使用函数时,我们写了\(f(x)=2x\),我们说表达式\(2x\)是定义范围内值的规则。 虽然序列是一个函数,但我们不使用通常的函数表示法。 与其将函数写成\(f(x)=2x\),不如将其写成\(a_{n}=2n\)。 \(a_{n}\)是序列的\(n\)第 th 项,位于\(n\) th 位置的项,其中,\(n\)是域中的一个值。 写出序列\(n\)第 th 项的公式称为序列的通用项或公式。
序列的通用项是从写入序列\(n\)第 th 项的公式中找到的。 序列的\(n\)第 th 项是位于\(n\)第 t 个位置的项,其中\(n\)是域中的一个值。\(a_{n}\)
当我们得到序列的通用项时,我们可以通过按顺序\(n\)替换为计数数字来找到这些项。 对于\(a_{n}=2 n\),
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(a_{n}\) | 2\(\cdot 1\) | 2\(\cdot 2\) | 2\(\cdot 3\) | 2\(\cdot 4\) | 2\(\cdot 5\) | 2\(\cdot 6\) |
| \(2\) | \(4\) | \(6\) | \(8\) | \(10\) |
\(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \ldots, \quad a_{n}, \dots\)
\(2, \quad 4, \quad 6, \quad 8, \quad10, \dots\)
为了找到序列的值,我们在计数数字中按顺序替换为该序列的通用项。
写下总术语为的序列的前五个项\(a_{n}=4 n-3\)。
解决方案:
我们按顺序将值\(1, 2, 3, 4\)替换\(5\)到公式\(a_{n}=4n−3\)中。
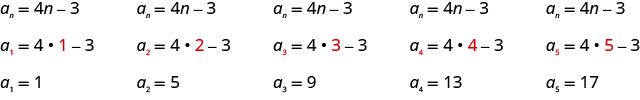
答案:
序列的前五个项是\(1, 5, 9, 13\)、和\(17\)。
写下总术语为的序列的前五个项\(a_{n}=3n-4\)。
- 回答
-
\(-1,2,5,8,11\)
写下总术语为的序列的前五个项\(a_{n}=2n-5\)。
- 回答
-
\(-3,-1,1,3,5\)
对于某些序列,变量是指数。
写下总术语为的序列的前五个项\(a_{n}=2^{n}+1\)。
解决方案:
我们按顺序将值\(1, 2, 3, 4\)替换\(5\)到公式\(a_{n}=2^{n}+1\)中。
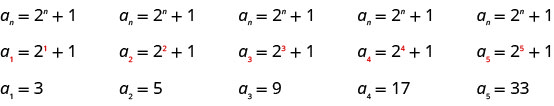
答案:
序列的前五个项是\(3, 5, 9, 17\)、和\(33\)。
写下总术语为的序列的前五个项\(a_{n}=3^{n}+4\)。
- 回答
-
\(7,13,31,85,247\)
写下总术语为的序列的前五个项\(a_{n}=2^{n}-5\)。
- 回答
-
\(-3,-1,3,11,27\)
看到序列的表达式\((−1)^{n}\)或\((−1)^{n+1}\)通用术语的情况并不少见。 如果我们为每个表达式求值几个值,则会发现该表达式与术语的符号交替出现。
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|
| \ (n\)” >\((-1)^{n}\) | \ (1\)” >\((-1)^{1}\) \(-1\) |
\ (2\)” >\((-1)^{2}\) 1 |
\ (3\)” >\((-1)^{3}\) \(-1\) |
\ (4\)” >\((-1)^{4}\) \(1\) |
\ (5\)” >\((-1)^{5}\) \(-1\) |
| \ (n\)” >\((-1)^{n+1}\) | \ (1\)” >\((-1)^{1+1}\) 1 |
\ (2\)” >\((-1)^{2+1}\) \(-1\) |
\ (3\)” >\((-1)^{3+1}\) 1 |
\ (4\)” >\((-1)^{4+1}\) \(-1\) |
\ (5\)” >\((-1)^{5+1}\) 1 |
\(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \dots, \quad a_{n}, \dots\)
\(\begin{array}{rrrr}{-1,} & {1,} & {-1,} & {1,} & {-1 \ldots} \\ {1,} & {-1,} & {1,} & {-1,} & {1 \ldots}\end{array}\)
写下总术语为的序列的前五个项\(a_{n}=(-1)^{n} n^{3}\)。
解决方案:
我们按顺序将值\(1, 2, 3, 4\)替换\(5\)到公式\(a_{n}=(-1)^{n} n^{3}\)中。
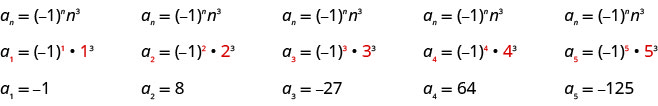
答案:
序列的前五个项是\(−1, 8, −27, 64, −1, 8, −27, 64\)、和\(−125\)。
写下总术语为的序列的前五个项\(a_{n}=(-1)^{n} n^{2}\)。
- 回答
-
\(-1,4,-9,16,-25\)
写下总术语为的序列的前五个项\(a_{n}=(-1)^{n+1} n^{3}\)。
- 回答
-
\(1,-8,27,-64,125\)
为序列的通用项(\(n\)第 1 项)找出公式
有时候我们有几个序列项,知道通用术语或\(n\)第 th 个术语会很有帮助。 为了找到通用术语,我们在术语中寻找模式。 这些模式通常涉及倍数或乘方。 我们还在术语符号中寻找一种模式。
为显示前五个项的序列找一个通用项。 \(4,8,12,16,20, \dots\)
解决方案:
-


我们在术语中寻找一种模式。 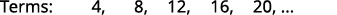
这些数字都是的倍数\(4\)。 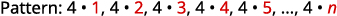
该序列的通用术语是\(a_{n}=4n\)。 表 12.1.4 答案:
该序列的通用术语是\(a_{n}=4n\)。
为显示前五个项的序列找一个通用项。
\(3,6,9,12,15, \dots\)
- 回答
-
\(a_{n}=3 n\)
为显示前五个项的序列找一个通用项。
\(5,10,15,20,25, \dots\)
- 回答
-
\(a_{n}=5 n\)
为显示前五个项的序列找一个通用项。 \(2,-4,8,-16,32, \dots\)
解决方案:
-
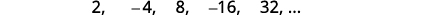
图 12.1.8 
图 12.1.9 我们在术语中寻找一种模式。 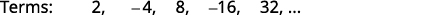
图 12.1.10 数字是的幂次方\(2\)。 信号交替出现,甚至是\(n\)负数。 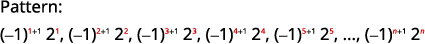
图 12.1.11 序列的通用术语是\(a_{n}=(-1)^{n+1} 2^{n}\) 表 12.1.5 答案:
该序列的通用术语是\(a_{n}=(-1)^{n+1}2^{n}\)。
为显示前五个项的序列找一个通用项。
\(-3,9,-27,81,-243, \dots\)
- 回答
-
\(a_{n}=(-1)^{n} 3^{n}\)
为显示前五个项的序列找一个通用项
\(1,-4,9,-16,25, \dots\)
- 回答
-
\(a_{n}=(-1)^{n+1} n^{2}\)
为显示前五个项的序列找一个通用项。 \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}, \frac{1}{243}, \dots\)
解决方案:
-
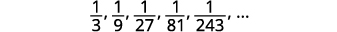
图 12.1.12 
图 12.1.13 我们在术语中寻找一种模式。 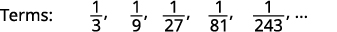
图 12.1.14 分子都是\(1\)。 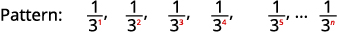
图 12.1.15 分母是的幂次方\(3\)。 该序列的通用术语是\(a_{n}=\frac{1}{3^{n}}\)。 表 12.1.6 答案:
该序列的通用术语是\(a_{n}=\frac{1}{3^{n}}\)。
为显示前五个项的序列找一个通用项。
\(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \dots\)
- 回答
-
\(a_{n}=\frac{1}{2^{n}}\)
为显示前五个项的序列找一个通用项。
\(\frac{1}{1}, \frac{1}{4}, \frac{1}{9}, \frac{1}{16}, \frac{1}{25}, \dots\)
- 回答
-
\(a_{n}=\frac{1}{n^{2}}\)
使用阶乘表示法
序列的项通常是连续整数的乘积。 我们用一种称为阶乘表示法的特殊符号来表示这些产品。 例如\(5!\),读取\(5\)阶乘,均值\(5⋅4⋅3⋅2⋅1\)。 这里的感叹号不是标点符号;它表示阶乘记法。
如果\(n\)是正整数,则\(n!\)为
\(n !=n(n-1)(n-2) \dots\)
我们定义\(0!\)为\(1\),所以\(0!=1\)。
显示\(n!\)了第一个\(5\)正整数的值。
\(\begin{array}{ccccc}{1 !} & {2 !} & {3 !} & {4 !} & {5 !} \\ {1} & \quad{2 \cdot 1} & \quad {3 \cdot 2 \cdot 1} & \quad{4 \cdot 3 \cdot 2 \cdot 1} & \quad {5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\ {1} & {2} & {6} & {24} & {120}\end{array}\)
写下总术语为的序列的前五个项\(a_{n}=\frac{1}{n !}\)。
解决方案:
我们按顺序将这些值替换\(1, 2, 3, 4, 5\)到公式\(a_{n}=\frac{1}{n !}\)中。
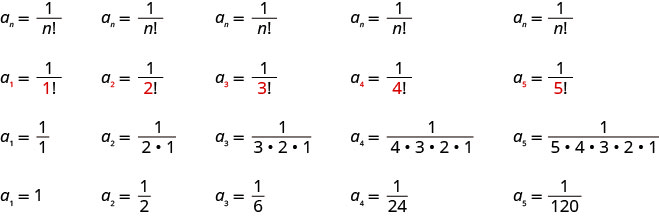
答案:
序列的前五个项是\(1, \frac{1}{2}, \frac{1}{6}, \frac{1}{24}, \frac{1}{120}\)。
写下总术语为的序列的前五个项\(a_{n}=\frac{2}{n !}\)。
- 回答
-
\(2,1, \frac{1}{3}, \frac{1}{12}, \frac{1}{60}\)
写下总术语为的序列的前五个项\(a_{n}=\frac{3}{n !}\)。
- 回答
-
\(3, \frac{3}{2}, \frac{1}{2}, \frac{1}{8}, \frac{1}{40}\)
当分子和分母中有阶乘的分数时,我们会将因子垂直排列以简化计算。
写下总术语为的序列的前五个项\(a_{n}=\frac{(n+1) !}{(n-1) !}\)。
解决方案:
我们按顺序将这些值替换\(1, 2, 3, 4, 5\)到公式\(a_{n}=\frac{(n+1) !}{(n-1) !}\)中。
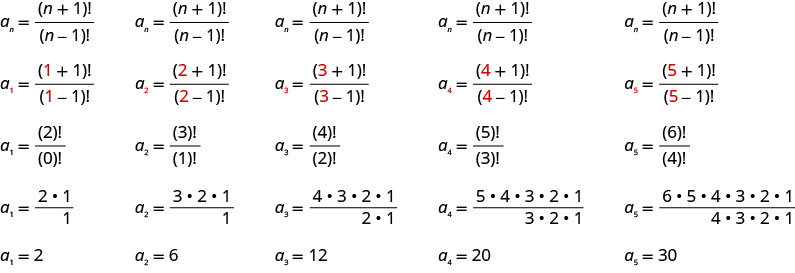
答案:
序列的前五个项是\(2, 6, 12, 20\)、和\(30\)。
写下序列的前五个项,其通用项为\(a_{n}=\frac{(n-1) !}{(n+1) !}\)
- 回答
-
\(\frac{1}{2}, \frac{1}{6}, \frac{1}{12}, \frac{1}{20}, \frac{1}{30}\)
写下总术语为的序列的前五个项\(a_{n}=\frac{n !}{(n+1) !}\)。
- 回答
-
\(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}\)
找出部分总和
有时,在应用程序中,添加序列的术语对我们来说很重要,而不仅仅是列出术语。 我们可以使用求和表示法,而不仅仅是将术语与加号连接起来。
例如,\(a_{1}+a_{2}+a_{3}+a_{4}+a_{5}\)可以写成\(\sum_{i=1}^{5} a_{i}\)。 我们将此读作 “\(a\)sub\(i\) 的总和\(i\)等于 1 到 5”。 符号\(∑\)表示相加,\(i\)是求和的索引。 \(1\)告诉我们从哪里开始(初始值),\(5\)告诉我们从哪里结束(终值)。
序列的第一\(n\)项之和用求和表示法写成,其\(n\)第 1\(a_{n}\) 项为:
\(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)
\(i\)这是求和的索引,\(1\)它告诉我们从哪里开始,\(n\)告诉我们从哪里结束。
当我们将有限数量的项相加时,我们将总和称为部分和。
展开部分总和并找到其值:\(\sum_{i=1}^{5} 2 i\)。
解决方案:
-
\(\sum_{i=1}^{5} 2 i\) 我们按顺序替\(1, 2, 3, 4, 5\)换值。 \(2 \cdot 1+2 \cdot 2+2 \cdot 3+2 \cdot 4 + 2 \cdot 5\) 简化。 \(2+4+6+8+10\) 添加。 \(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\) 表 12.1.7 答案:
\(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\)
展开部分总和并找到其值:\(\sum_{i=1}^{5} 3 i\)。
- 回答
-
\(45\)
展开部分总和并找到其值:\(\sum_{i=1}^{5} 4 i\)。
- 回答
-
\(60\)
索引不一定总是\(i\)我们可以使用任何字母\(i\),而是\(k\)常用的。 索引不必以任何一个开头\(1\),它可以以任何正整数开头和结尾。
展开部分总和并找到其值:\(\sum_{k=0}^{3} \frac{1}{k !}\)。
解决方案:
\(\begin{array}{c c} {}&{\sum_{k=0}^{3} \frac{1}{k !}} \\ {We\:substitute\:the\:values\:0,1,2,3\:in\:order.}&{\frac{1}{1}+\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}} \\ {Evaluate\:the\:factorials.}& {\frac{1}{1}+\frac{1}{1}+\frac{1}{2 !}+\frac{1}{6}} \\ {Simplify.}&{1+1+\frac{3}{6}+\frac{1}{6}} \\{Simplify.}& {\frac{16}{6}} \\ {Simplify.}&{\frac{8}{3}} \\{}& {\sum_{k=0}^{3} \frac{1}{k !}=\frac{8}{3}}\end{array}\)
展开部分总和并找到其值:\(\sum_{k=0}^{3} \frac{2}{k !}\)。
- 回答
-
\(\frac{16}{3}\)
展开部分总和并找到其值:\(\sum_{k=0}^{3} \frac{3}{k !}\)。
- 回答
-
\(8\)
使用求和表示法写出总和
在最后两个例子中,我们从求和表示法转变为写出总和。 现在我们将从求和开始,并将其更改为求和表示法。 这与查找序列的通用术语非常相似。 我们需要研究这些术语并找到一种模式。 这些模式通常涉及倍数或乘方。
使用求和表示法写出总和:\(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}\)。
解决方案:
\(\begin{array} {}&{ 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}} \\ {}&{n : 1,2,3,4,5} \\ {\text{We look for a pattern in the terms.}}&{\text { Terms: } 1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}} \\ {\text{The numerators are all one.}}&{\text { Pattern: } \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots \frac{1}{n}} \\ {\text{The denominators are the counting numbers from one to five.}}&{\text{The sum written in summation notation}} \\ {}&{1 + \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}=\sum^{5}_{n=1} \frac{1}{n}.} \end{array}\)
使用求和表示法写出总和:\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\)。
- 回答
-
\(\sum_{n=1}^{5} \frac{1}{2^{n}}\)
使用求和表示法写出总和:\(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}\)
- 回答
-
\(\sum_{n=1}^{5} \frac{1}{n^{2}}\)
当总和的项具有负系数时,我们必须仔细分析符号的模式。
使用求和表示法写出总和:\(-1+8-27+64-125\)。
解决方案:
-
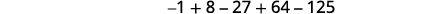
图 12.1.18 
图 12.1.19 我们在术语中寻找一种模式。 
图 12.1.20 术语的符号交替出现
,奇数项为负数。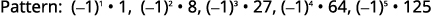
图 12.1.21 数字是从一到五的
计数数字的立方体。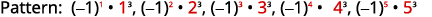
图 12.1.22 
图 12.1.23 用求和表示法写的总和是 \(-1+8-27+64-125=\sum_{n=1}^{5}(-1)^{n} \cdot n^{3}\) 表 12.1.8
使用求和表示法写出每个总和:\(1-4+9-16+25\)。
- 回答
-
\(\sum_{n=1}^{5}(-1)^{n+1} n^{2}\)
使用求和表示法写出每个总和:\(-2+4-6+8-10\)。
- 回答
-
\(\sum_{n=1}^{5}(-1)^{n} 2 n\)
访问此在线资源以获取更多指导和序列练习。
关键概念
- 阶乘表示法
如果\(n\)是正整数,则\(n!\)为
\(n !=n(n-1)(n-2) \ldots(3)(2)(1)\)
我们定义\(0!\)为\(1\),所以\(0!=1\)
- 求和表示法
序列的第一\(n\)项之和,其\(n\)第 1 项用求和表示法书写\(a_{n}\)为:
\(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)
\(i\)这是求和的索引,\(1\)它告诉我们从哪里开始,\(n\)告诉我们从哪里结束。
词汇表
- 有限序列
- 一种序列,其域限制为有限数量的计数数。
- 序列的通用术语
- 序列的通用术语是写出序列\(n\)第 th 项的公式。 序列的\(n\)第 th 项是位于\(n\)第 t 个位置的项,其中\(n\)是域中的一个值。\(a_{n}\)
- 无限序列
- 一种序列,其域全部是计数数字,并且有无限数量的计数数字。
- 部分总和
- 当我们将一个序列的有限数量的项相加时,我们将总和称为部分和。
- 顺序
- 序列是一个函数,其域是计数数字。


