第 9 章复习练习
- Page ID
- 204136
章节复习练习
使用平方根属性求解二次方程
在以下练习中,使用平方根属性求解。
- \(y^{2}=144\)
- \(n^{2}-80=0\)
- \(4 a^{2}=100\)
- \(2 b^{2}=72\)
- \(r^{2}+32=0\)
- \(t^{2}+18=0\)
- \(\frac{2}{3} w^{2}-20=30\)
- \(5 c^{2}+3=19\)
- 回答
-
1。 \(y=\pm 12\)
3。 \(a=\pm 5\)
5。 \(r=\pm 4 \sqrt{2} i\)
7。 \(w=\pm 5 \sqrt{3}\)
在以下练习中,使用平方根属性求解。
- \((p-5)^{2}+3=19\)
- \((u+1)^{2}=45\)
- \(\left(x-\frac{1}{4}\right)^{2}=\frac{3}{16}\)
- \(\left(y-\frac{2}{3}\right)^{2}=\frac{2}{9}\)
- \((n-4)^{2}-50=150\)
- \((4 c-1)^{2}=-18\)
- \(n^{2}+10 n+25=12\)
- \(64 a^{2}+48 a+9=81\)
- 回答
-
1。 \(p=-1,9\)
3。 \(x=\frac{1}{4} \pm \frac{\sqrt{3}}{4}\)
5。 \(n=4 \pm 10 \sqrt{2}\)
7。 \(n=-5 \pm 2 \sqrt{3}\)
通过完成正方形求解二次方程
在以下练习中,完成正方形以形成完美的三项式方形。 然后将结果写成二项式平方。
- \(x^{2}+22 x\)
- \(m^{2}-8 m\)
- \(a^{2}-3 a\)
- \(b^{2}+13 b\)
- 回答
-
1。 \((x+11)^{2}\)
3。 \(\left(a-\frac{3}{2}\right)^{2}\)
在以下练习中,通过完成方块来求解。
- \(d^{2}+14 d=-13\)
- \(y^{2}-6 y=36\)
- \(m^{2}+6 m=-109\)
- \(t^{2}-12 t=-40\)
- \(v^{2}-14 v=-31\)
- \(w^{2}-20 w=100\)
- \(m^{2}+10 m-4=-13\)
- \(n^{2}-6 n+11=34\)
- \(a^{2}=3 a+8\)
- \(b^{2}=11 b-5\)
- \((u+8)(u+4)=14\)
- \((z-10)(z+2)=28\)
- 回答
-
1。 \(d=-13,-1\)
3。 \(m=-3 \pm 10 i\)
5。 \(v=7 \pm 3 \sqrt{2}\)
7。 \(m=-9,-1\)
9。 \(a=\frac{3}{2} \pm \frac{\sqrt{41}}{2}\)
11。 \(u=-6 \pm 2 \sqrt{2}\)
\(ax^{2}+bx+c=0\)通过完成正方形求解表格的二次方程
在以下练习中,通过完成方块来求解。
- \(3 p^{2}-18 p+15=15\)
- \(5 q^{2}+70 q+20=0\)
- \(4 y^{2}-6 y=4\)
- \(2 x^{2}+2 x=4\)
- \(3 c^{2}+2 c=9\)
- \(4 d^{2}-2 d=8\)
- \(2 x^{2}+6 x=-5\)
- \(2 x^{2}+4 x=-5\)
- 回答
-
1。 \(p=0,6\)
3。 \(y=-\frac{1}{2}, 2\)
5。 \(c=-\frac{1}{3} \pm \frac{2 \sqrt{7}}{3}\)
7。 \(x=\frac{3}{2} \pm \frac{1}{2} i\)
在以下练习中,使用二次公式求解。
- \(4 x^{2}-5 x+1=0\)
- \(7 y^{2}+4 y-3=0\)
- \(r^{2}-r-42=0\)
- \(t^{2}+13 t+22=0\)
- \(4 v^{2}+v-5=0\)
- \(2 w^{2}+9 w+2=0\)
- \(3 m^{2}+8 m+2=0\)
- \(5 n^{2}+2 n-1=0\)
- \(6 a^{2}-5 a+2=0\)
- \(4 b^{2}-b+8=0\)
- \(u(u-10)+3=0\)
- \(5 z(z-2)=3\)
- \(\frac{1}{8} p^{2}-\frac{1}{5} p=-\frac{1}{20}\)
- \(\frac{2}{5} q^{2}+\frac{3}{10} q=\frac{1}{10}\)
- \(4 c^{2}+4 c+1=0\)
- \(9 d^{2}-12 d=-4\)
- 回答
-
1。 \(x=\frac{1}{4}, 1\)
3。 \(r=-6,7\)
5。 \(v=\frac{-1 \pm \sqrt{21}}{8}\)
7。 \(m=\frac{-4 \pm \sqrt{10}}{3}\)
9。 \(a=\frac{5}{12} \pm \frac{\sqrt{23}}{12} i\)
11。 \(u=5 \pm \sqrt{21}\)
13。 \(p=\frac{4 \pm \sqrt{5}}{5}\)
15。 \(c=-\frac{1}{2}\)
在以下练习中,确定每个二次方程的解数。
-
- \(9 x^{2}-6 x+1=0\)
- \(3 y^{2}-8 y+1=0\)
- \(7 m^{2}+12 m+4=0\)
- \(5 n^{2}-n+1=0\)
-
- \(5 x^{2}-7 x-8=0\)
- \(7 x^{2}-10 x+5=0\)
- \(25 x^{2}-90 x+81=0\)
- \(15 x^{2}-8 x+4=0\)
- 回答
-
1。
- \(1\)
- \(2\)
- \(2\)
- \(2\)
在以下练习中,确定用于求解每个二次方程的最合适的方法(因子分解、平方根或二次公式)。 不要解决。
-
- \(16 r^{2}-8 r+1=0\)
- \(5 t^{2}-8 t+3=9\)
- \(3(c+2)^{2}=15\)
-
- \(4 d^{2}+10 d-5=21\)
- \(25 x^{2}-60 x+36=0\)
- \(6(5 v-7)^{2}=150\)
- 回答
-
1。
- 因子
- 二次公式
- 平方根
以二次形式求解方程
在以下练习中,求解。
- \(x^{4}-14 x^{2}+24=0\)
- \(x^{4}+4 x^{2}-32=0\)
- \(4 x^{4}-5 x^{2}+1=0\)
- \((2 y+3)^{2}+3(2 y+3)-28=0\)
- \(x+3 \sqrt{x}-28=0\)
- \(6 x+5 \sqrt{x}-6=0\)
- \(x^{\frac{2}{3}}-10 x^{\frac{1}{3}}+24=0\)
- \(x+7 x^{\frac{1}{2}}+6=0\)
- \(8 x^{-2}-2 x^{-1}-3=0\)
- 回答
-
1。 \(x=\pm \sqrt{2}, x=\pm 2 \sqrt{3}\)
3。 \(x=\pm 1, x=\pm \frac{1}{2}\)
5。 \(x=16\)
7。 \(x=64, x=216\)
9。 \(x=-2, x=\frac{4}{3}\)
求解二次方程的应用
在以下练习中,使用分解法、平方根原理或二次公式求解。 如果需要,将答案四舍五入到最接近的十分之一。
- 找出乘积为的两个连续奇数\(323\)。
- 找出乘积为的两个连续偶数\(624\)。
- 三角形横幅的面积为\(351\)平方厘米。 底座的长度比高度的四倍长两厘米。 找出底座的高度和长度。
- 朱利叶斯为他的硬币收藏制作了一个三角形陈列柜。 展示柜的高度小于底座宽度的两倍六英寸。 表壳背面的面积为\(70\)平方英寸。 找出表壳的高度和宽度。
- 直角三角形形状的瓷砖马赛克被用作矩形路径的拐角。 马赛克的斜边是\(5\)英尺。 马赛克的一面长度是另一面的两倍。 两边的长度是多少? 四舍五入到最接近的十分之一。

图 9.E.1
6。 一块矩形胶合板的对角线比宽度多两英尺。 胶合板的长度是宽度的两倍。 胶合板对角线的长度是多少? 四舍五入到最接近的十分之一。
7。 从街道到帕姆家的前面步行面积为\(250\)平方英尺. 它的长度比其宽度的四倍小两倍。 找到人行道的长度和宽度。 四舍五入到最接近的十分之一。
8。 在索菲亚的毕业典礼上,将端到尾排列几张相同宽度的桌子,以提供总面积为\(75\)平方英尺的餐桌。 表格的总长度将比宽度的三倍多两倍。 找到餐桌的长度和宽度,这样 Sophia 就可以购买正确尺寸的桌布。 将答案四舍五入到最接近的十分之一。
9。 球以\(160\)英尺/秒的速度垂直向空中投掷。 使用公式\(h=-16 t^{2}+v_{0} t\)来确定球何时会离地面几\(384\)英尺。 四舍五入到最接近的十分之一。
10。 这对夫妇乘坐小型飞机快速飞往葡萄酒之乡享用浪漫晚餐,然后返回家中。 飞机总共飞行了\(5\)几个小时,单程行程为\(360\)数英里. 如果飞机以\(150\)英里/小时的速度飞行,那么影响飞机的风速是多少?
11。 以斯拉在河上划皮划艇,然后在总共\(6\)几个小时内返回. 这次旅行单程长达\(4\)数英里,潮流很艰难。 如果罗伊以\(5\)英里/小时的速度划皮艇,那么目前的速度是多少?
12。 如果两个杂工一起工作,他们可以在\(2\)几个小时内完成房屋维修。 其中一个人比另一个人多花\(3\)几个小时才能独自完成工作。 每个杂工单独进行房屋维修需要多长时间?
- 回答
-
2。 乘积为 and\(24\) 和\(26\) and\(624\) 的两个连续偶数\(−26\)。\(−24\)
4。 高度为\(14\)英寸,宽度为\(10\)英寸。
6。 对角线的长度为\(3.6\)英尺。
8。 餐桌的宽度为\(4.7\)英尺,长度为\(16.1\)英尺。
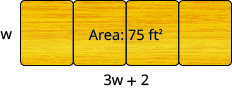
图 9.E.2 10。 风速为\(30\)英里每小时.
12。 一个人要花\(3\)几个小时,另一个人要花\(6\)几个小时才能独自完成维修。
使用属性绘制二次函数图
在以下练习中,逐点绘图。
- 图表\(y=x^{2}-2\)
- 图表\(y=-x^{2}+3\)
- 回答
-
2。
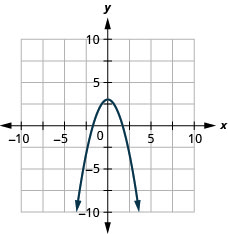
图 9.E.3
在以下练习中,确定以下抛物线是向上还是向下打开。
-
- \(y=-3 x^{2}+3 x-1\)
- \(y=5 x^{2}+6 x+3\)
-
- \(y=x^{2}+8 x-1\)
- \(y=-4 x^{2}-7 x+1\)
- 回答
-
2。
- 向上
- 向下
在以下练习中,找到
- 对称轴方程
- 顶点
- \(y=-x^{2}+6 x+8\)
- \(y=2 x^{2}-8 x+1\)
- 回答
-
2。 \(x=2\);\((2,-7)\)
在以下练习中,找到\(x\)-和\(y\)-截取。
- \(y=x^{2}-4x+5\)
- \(y=x^{2}-8x+15\)
- \(y=x^{2}-4x+10\)
- \(y=-5x^{2}-30x-46\)
- \(y=16x^{2}-8x+1\)
- \(y=x^{2}+16x+64\)
- 回答
-
2。 \(\begin{array}{l}{y :(0,15)} \\ {x :(3,0),(5,0)}\end{array}\)
4。 \(\begin{array}{l}{y :(0,-46)} \\ {x : \text { none }}\end{array}\)
6。 \(\begin{array}{l}{y :(0,-64)} \\ {x :(-8,0)}\end{array}\)
使用属性绘制二次函数图
在以下练习中,使用其属性绘制图表。
- \(y=x^{2}+8 x+15\)
- \(y=x^{2}-2 x-3\)
- \(y=-x^{2}+8 x-16\)
- \(y=4 x^{2}-4 x+1\)
- \(y=x^{2}+6 x+13\)
- \(y=-2 x^{2}-8 x-12\)
- 回答
-
2。
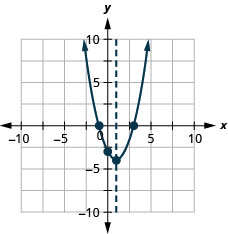
图 9.E.4 4。
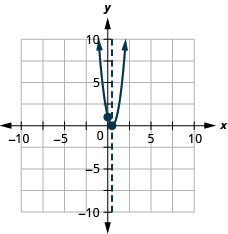
图 9.E.5 6。
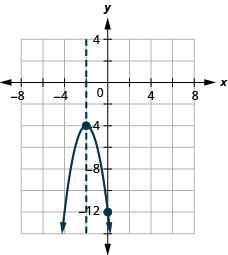
图 9.E.6
在以下练习中,找到最小值或最大值。
- \(y=7 x^{2}+14 x+6\)
- \(y=-3 x^{2}+12 x-10\)
- 回答
-
2。 最大值为 wh\(2\) en\(x=2\)。
在以下练习中,求解。 将答案四舍五入到最接近的十分之一。
- 球从地面向上投掷,初始速度为\(112\) ft/sec。 使用二次方程计算\(h=-16 t^{2}+112 t\)球达到最大高度需要多长时间,然后找到最大高度。
- 日托设施在建筑物侧面封闭了一个矩形区域,供孩子们在户外玩耍。 他们需要在院子的三边使用几\(180\)英尺的围栏来最大限度地扩大面积。 二次方程\(A=-2 x^{2}+180 x\)给出了与院子接壤的建筑物的长度占码的面积。\(A\)\(x\) 找到应与院子接壤的建筑物的长度以最大化面积,然后找到最大面积。

- 回答
-
2。 与建筑物相邻的长度为\(90\)英尺,最大面积为\(4,050\)平方英尺。
使用变换绘制二次函数图
在以下练习中,使用垂直移位绘制每个函数的图表。
- \(g(x)=x^{2}+4\)
- \(h(x)=x^{2}-3\)
- 回答
-
2。
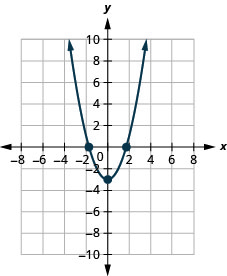
图 9.E.8
在以下练习中,使用水平移位绘制每个函数的图表。
- \(f(x)=(x+1)^{2}\)
- \(g(x)=(x-3)^{2}\)
- 回答
-
2。
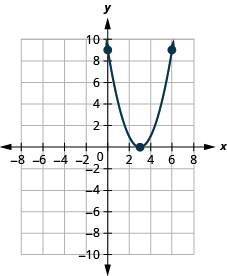
图 9.E.9
在以下练习中,使用转换绘制每个函数的图表。
- \(f(x)=(x+2)^{2}+3\)
- \(f(x)=(x+3)^{2}-2\)
- \(f(x)=(x-1)^{2}+4\)
- \(f(x)=(x-4)^{2}-3\)
- 回答
-
2。
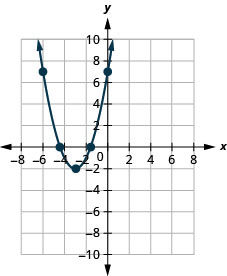
图 9.E.10 4。
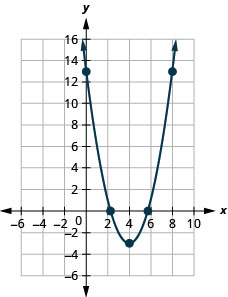
图 9.E.11
在以下练习中,绘制每个函数的图表。
- \(f(x)=2x^{2}\)
- \(f(x)=-x^{2}\)
- \(f(x)=\frac{1}{2} x^{2}\)
- 回答
-
2。
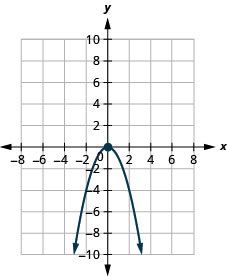
图 9.E.12
在以下练习中,通过填写方块来重写\(f(x)=a(x-h)^{2}+k\)表单中的每个函数。
- \(f(x)=2 x^{2}-4 x-4\)
- \(f(x)=3 x^{2}+12 x+8\)
- 回答
-
1。 \(f(x)=2(x-1)^{2}-6\)
在以下练习中,
- 以\(f(x)=a(x−h)^{2}+k\)表单重写每个函数
- 使用转换将其绘制成图形
- \(f(x)=3 x^{2}-6 x-1\)
- \(f(x)=-2 x^{2}-12 x-5\)
- \(f(x)=2 x^{2}+4 x+6\)
- \(f(x)=3 x^{2}-12 x+7\)
- 回答
-
1。
- \(f(x)=3(x-1)^{2}-4\)
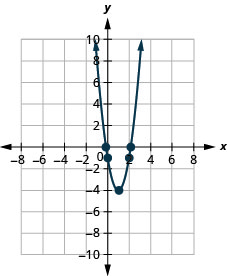
图 9.E.13
3。
- \(f(x)=2(x+1)^{2}+4\)
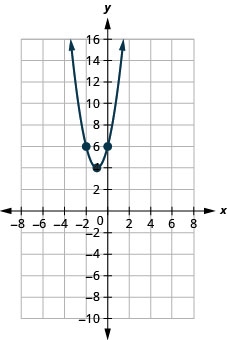
图 9.E.14
在以下练习中,
- 以\(f(x)=a(x−h)^{2}+k\)表单重写每个函数
- 使用属性绘制图表
- \(f(x)=-3 x^{2}-12 x-5\)
- \(f(x)=2 x^{2}-12 x+7\)
- 回答
-
1。
- \(f(x)=-3(x+2)^{2}+7\)
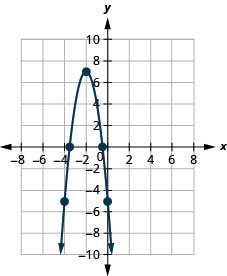
图 9.E.15
在以下练习中,以\(f(x)=a(x−h)^{2}+k\)形式写下二次函数。
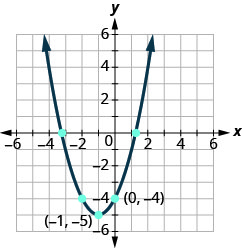
图 9.E.16
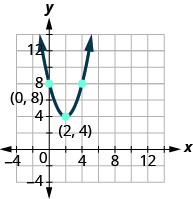
图 9.E.17
- 回答
-
1。 \(f(x)=(x+1)^{2}-5\)
求解二次不等式
在以下练习中,以图形方式求解并用区间表示法写出解。
- \(x^{2}-x-6>0\)
- \(x^{2}+4 x+3 \leq 0\)
- \(-x^{2}-x+2 \geq 0\)
- \(-x^{2}+2 x+3<0\)
- 回答
-
1。
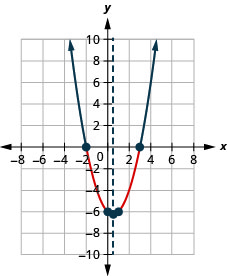
图 9.E.18- \((-\infty,-2) \cup(3, \infty)\)
3。
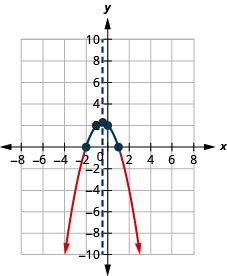
图 9.E.19- \([-2,1]\)
在以下练习中,用代数求解每个不等式,并用区间表示法写出任何解。
- \(x^{2}-6 x+8<0\)
- \(x^{2}+x>12\)
- \(x^{2}-6 x+4 \leq 0\)
- \(2 x^{2}+7 x-4>0\)
- \(-x^{2}+x-6>0\)
- \(x^{2}-2 x+4 \geq 0\)
- 回答
-
1。 \((2,4)\)
3。 \([3-\sqrt{5}, 3+\sqrt{5}]\)
5. 没有解决办法
练习测试
- 使用平方根属性求解二次方程\(3(w+5)^{2}=27\)。
- 使用完成方程来求解二次方程\(a^{2}-8 a+7=23\)。
- 使用二次公式求解二次方程\(2 m^{2}-5 m+3=0\)。
- 回答
-
1。 \(w=-2, w=-8\)
3。 \(m=1, m=\frac{3}{2}\)
求解以下二次方程。 使用任何方法。
- \(2 x(3 x-2)-1=0\)
- \(\frac{9}{4} y^{2}-3 y+1=0\)
- 回答
-
2。 \(y=\frac{2}{3}\)
使用判别来确定每个二次方程解的数量和类型。
- \(6 p^{2}-13 p+7=0\)
- \(3 q^{2}-10 q+12=0\)
- 回答
-
2。 \(2\)复杂
求解每个方程。
- \(4 x^{4}-17 x^{2}+4=0\)
- \(y^{\frac{2}{3}}+2 y^{\frac{1}{3}}-3=0\)
- 回答
-
2。 \(y=1, y=-27\)
对于每个抛物线,找到
- 它朝哪个方向开启
- 对称轴方程
- 顶点
- \(x\)- 和\(y\)-拦截
- 最大值或最小值
- \(y=3 x^{2}+6 x+8\)
- \(y=-x^{2}-8 x+16\)
- 回答
-
2。
- 向下
- \(x=-4\)
- \((-4,0)\)
- \(y: (0,16); x: (-4,0)\)
- when 的最\(-4\)小值\(x=0\)
使用截距、顶点和对称轴方程绘制每个二次函数的图形。
- \(f(x)=x^{2}+6 x+9\)
- \(f(x)=-2 x^{2}+8 x+4\)
- 回答
-
2。
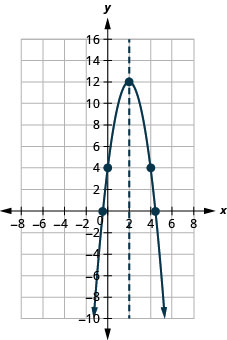
图 9.E.20
在以下练习中,使用转换绘制每个函数的图表。
- \(f(x)=(x+3)^{2}+2\)
- \(f(x)=x^{2}-4 x-1\)
- 回答
-
2。
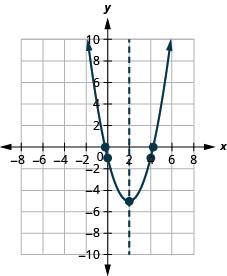
图 9.E.21
在以下练习中,用代数求解每个不等式,并用区间表示法写出任何解。
- \(x^{2}-6 x-8 \leq 0\)
- \(2 x^{2}+x-10>0\)
- 回答
-
2。 \(\left(-\infty,-\frac{5}{2}\right) \cup(2, \infty)\)
使用二次方程对情况进行建模,然后用任何方法求解。
- 找出乘积为的两个连续偶数\(360\)。
- 矩形对角线的长度比宽度多三倍。 矩形的长度是宽度的三倍。 找出对角线的长度。 (四舍五入到最接近的十分之一。)
- 回答
-
2。 水气球以\(86\)英尺/秒的速度向上发射。 使用公式计算\(h=-16 t^{2}+86 t\)气球达到最大高度需要多长时间,然后找到最大高度。 四舍五入到最接近的十分之一。


