9.2:使用平方根属性求解二次方程
- Page ID
- 204068
在本节结束时,您将能够:
- \(ax^{2}=k\)使用平方根属性求解形式的二次方程
- \(a(x–h)^{2}=k\)使用平方根属性求解形式的二次方程
在开始之前,请参加这个准备测验。
- 简化:\(\sqrt{128}\)。
如果您错过了此问题,请查看示例 8.13。 - 简化:\(\sqrt{\frac{32}{5}}\)。
如果您错过了此问题,请查看示例 8.50。 - 因子:\(9 x^{2}-12 x+4\)。
如果您错过了此问题,请查看示例 6.23。
二次方程是形式的方程\(a x^{2}+b x+c=0\),其中\(a≠0\)。 二次方程与线性方程的不同之处在于,二次方程包含一个二次项,变量提高到该形式的二次方\(ax^{2}\)。 我们使用与线性方程不同的方法来求解二次方程,因为仅仅相加、减去、乘和除项并不能隔离变量。
我们已经看到,一些二次方程可以通过分解来求解。 在本章中,我们将学习其他三种在无法分解二次方程的情况下使用的方法。
\(ax^{2}=k\)使用平方根属性求解形式的二次方程
我们已经通过分解求解了一些二次方程。 让我们回顾一下我们是如何使用分解来求解二次方程的\(x^{2}=9\)。
\(x^{2}=9\)
将方程式以标准形式表示。
\(x^{2}-9=0\)
将平方差分解为因子。
\((x-3)(x+3)=0\)
使用 “零产量” 属性。
\(x-3=0 \quad x-3=0\)
求解每个方程。
\(x=3 \quad x=-3\)
我们可以很容易地使用因子分解来找到相似方程的解,比如\(x^{2}=16\)和\(x^{2}=25\),因为\(16\)和\(25\)是完美的正方形。 在每种情况下,我们都会得到两个解决方案\(x=4, x=-4\),\(x=5, x=-5\)
但是当我们有这样的方程式时会发生什么\(x^{2}=7\)? 由于\(7\)不是完美的正方形,因此我们无法通过分解来求解方程。
之前我们了解到 s\(169\) ince 是的平方\(13\),我们也可以说\(13\)这是的平方根\(169\)。 另外\((-13)^{2}=169\),的平方根\(−13\)也是如此\(169\)。 因此,\(13\)和\(−13\)都是的平方根\(169\)。 因此,每个正数都有两个平方根——一个正数和一个负数。 我们之前用这种方式定义了数字的平方根:
如果\(n^{2}=m\),\(n\)则为的平方根\(m\)。
由于这些方程都是形式上的\(x^{2}=k\),因此平方根定义告诉我们,解是两个平方根\(k\)。 这就产生了平方根属性。
平方根属性
如果\(x^{2}=k\),那么
\(x=\sqrt{k} \quad\)或者\(\quad x=-\sqrt{k} \quad\)或\(\quad x=\pm \sqrt{k}\)
请注意,Square Root Property 给出了形式的方程的两个解\(x^{2}=k\),即主平方根\(k\)和相反的方程。 我们也可以将解决方案写成\(x=\pm \sqrt{k}\)。 我们将其理解为\(x\)等于正或负的平方根\(k\)。
现在我们将\(x^{2}=9\)再次求解方程,这次是使用平方根属性。
\(\begin{aligned} &x^{2} =9 \\ \text { Use the Square Root Property. } \quad& x=\pm \sqrt{9} \\& x =\pm 3 \end{aligned}\)
所以\(x=3\)或者\(x=-3\)
当常量不是完美正方形时会发生什么? 让我们使用平方根属性来求解方程\(x^{2}=7\)。
\(x^{2}=7\)
使用平方根属性。 \(x=\sqrt{7}, \quad x=-\sqrt{7}\)
我们无法简化\(\sqrt{7}\),所以我们把答案当作激进的答案。
解决:\(x^{2}-50=0\)。
解决方案:
| 步骤 1:分离二次项并将其系数设为一。 | 加\(50\)到两边就可以自己\(x^{2}\)动手。 | \(\begin{aligned} x^{2}-50 &=0 \\ x^{2} &=50 \end{aligned}\) |
| 步骤 2:使用平方根属性。 | 记得写下\(\pm\)符号。 | \(x=\pm \sqrt{50}\) |
| 第 3 步:简化激进。 | 重写以显示两个解决方案。 | \(\begin{array}{l}{x=\pm \sqrt{25} \cdot \sqrt{2}} \\ {x=\pm 5 \sqrt{2}} \\ {}x=5\sqrt{2}, \:x=-5\sqrt{2}\end{array}\) |
| 第 4 步:检查解决方案。 | 在\(x=5 \sqrt{2}\)和中替换\(x=-5 \sqrt{2}\) |
\(\begin{array}{r}{x^{2}-50=0} \\ {(\color{red}{5 \sqrt{2}}\color{black}{)}^{2}-50 \stackrel{?}{=} 0} \\ {25 \cdot 2-50 \stackrel{?}{=} 0} \\ {0=0}\end{array}\) \(\begin{array}{r}{x^{2}-50=0} \\ {(\color{red}{-5 \sqrt{2}}\color{black}{)}^{2}-50 \stackrel{?}{=} 0} \\ {25 \cdot 2-50 \stackrel{?}{=} 0} \\ {0=0}\end{array}\) |
解决:\(x^{2}-48=0\)。
- 回答
-
\(x=4 \sqrt{3}, x=-4 \sqrt{3}\)
解决:\(y^{2}-27=0\)。
- 回答
-
\(y=3 \sqrt{3}, y=-3 \sqrt{3}\)
此处列出了使用平方根属性求解二次方程所要采取的步骤。
使用平方根属性求解二次方程
- 分离二次项并将其系数设为一。
- 使用平方根属性。
- 简化激进。
- 检查解决方案。
要使用平方根属性,变量项的系数必须等于 1。 在下一个示例中,在使用平方根属性\(3\)之前,我们必须将方程的两边除以系数。
解决:\(3 z^{2}=108\)。
解决方案:
| \(3 z^{2}=108\) | |
| 二次项是孤立的。 除\(3\)以得出其系数\(1\)。 | \(\frac{3 z^{2}}{3}=\frac{108}{3}\) |
| 简化。 | \(z^{2}=36\) |
| 使用平方根属性。 | \(z=\pm \sqrt{36}\) |
| 简化激进。 | \(z=\pm 6\) |
| 重写以显示两个解决方案。 | \(z=6, \quad z=-6\) |
|
查看解决方案: 
|
解决:\(2x^{2}=98\)。
- 回答
-
\(x=7, x=-7\)
解决:\(5m^{2}=80\)。
- 回答
-
\(m=4, m=-4\)
平方根属性指出 “如果”\(x^{2}=k\),会发生什么\(k<0\)? 在下一个示例中,情况将如此。
解决:\(x^{2}+72=0\)。
解决方案:
| \(x^{2}+72=0\) | |
| 分离二次项。 | \(x^{2}=-72\) |
| 使用平方根属性。 | \(x=\pm \sqrt{-72}\) |
| 简化复数的使用。 | \(x=\pm \sqrt{72} i\) |
| 简化激进。 | \(x=\pm 6 \sqrt{2} i\) |
| 重写以显示两个解决方案 | \(x=6 \sqrt{2} i, x=-6 \sqrt{2} i\) |
|
查看解决方案: 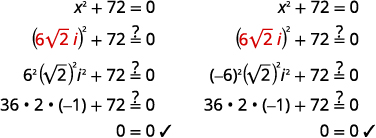
|
解决:\(c^{2}+12=0\)。
- 回答
-
\(c=2 \sqrt{3} i, \quad c=-2 \sqrt{3} i\)
解决:\(q^{2}+24=0\)。
- 回答
-
\(c=2 \sqrt{6} i, \quad c=-2 \sqrt{6} i\)
当方程中出现分数时,我们的方法也适用,我们像任何带有分数的方程一样求解。 在下一个示例中,我们首先分离二次项,然后使系数等于一。
解决:\(\frac{2}{3} u^{2}+5=17\)。
解决方案:
| \(\frac{2}{3} u^{2}+5=17\) | |
| 分离二次项。 | 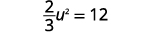 |
| 乘\(\frac{3}{2}\)以得出系数\(1\)。 | 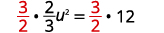 |
| 简化。 | 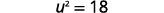 |
| 使用平方根属性。 | 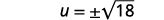 |
| 简化激进。 | 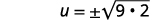 |
| 简化。 | 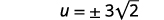 |
| 重写以显示两个解决方案。 |  |
|
查看: 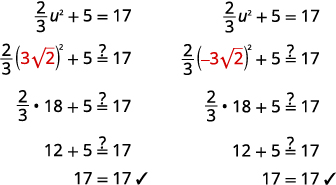
|
解决:\(\frac{1}{2} x^{2}+4=24\)。
- 回答
-
\(x=2 \sqrt{10}, x=-2 \sqrt{10}\)
解决:\(\frac{3}{4} y^{2}-3=18\)。
- 回答
-
\(y=2 \sqrt{7}, y=-2 \sqrt{7}\)
某些方程的解在自由基内部可能有分数。 当这种情况发生时,我们必须使分母合理化。
解决:\(2 x^{2}-8=41\)。
解决方案:
 |
|
| 分离二次项。 |  |
| 除\(2\)以得出系数\(1\)。 | 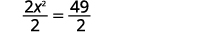 |
| 简化。 | 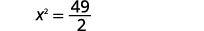 |
| 使用平方根属性。 | 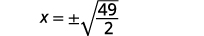 |
| 将基数重写为平方根的分数。 | 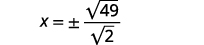 |
| 合理化分母。 | 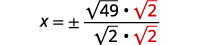 |
| 简化。 | 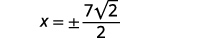 |
| 重写以显示两个解决方案。 | 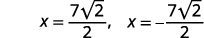 |
|
查看: 我们把支票留给你。 |
解决:\(5 r^{2}-2=34\)。
- 回答
-
\(r=\frac{6 \sqrt{5}}{5}, \quad r=-\frac{6 \sqrt{5}}{5}\)
解决:\(3 t^{2}+6=70\)。
- 回答
-
\(t=\frac{8 \sqrt{3}}{3}, \quad t=-\frac{8 \sqrt{3}}{3}\)
\(a(x-h)^{2}=k\)使用平方根属性求解形式的二次方程
我们也可以使用平方根属性来求解这种\(a(x-h)^{2}=k\)形式的方程。 请注意,原始形式的二\(x\)次项被替换\(ax^{2}=k\)为\((x-h)\)。
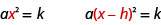
和以前一样,第一步是分离变量为平方的项。 在这种情况下,正在对二项式进行平方。 隔离二项式后,通过将两边除以系数\(a\),就可以使用平方根属性\((x-h)^{2}\)了。
解决:\(4(y-7)^{2}=48\)。
解决方案:
| \(4(y-7)^{2}=48\) | |
| 将两边除以系数\(4\)。 | \((y-7)^{2}=12\) |
| 在二项式上使用平方根属性。 | \(y-7=\pm \sqrt{12}\) |
| 简化激进。 | \(y-7=\pm 2 \sqrt{3}\) |
| 求解\(y\)。 | \(y=7 \pm 2 \sqrt{3}\) |
| 重写以显示两个解决方案。 | \(y=7+2 \sqrt{3}\) \(y=7-2 \sqrt{3}\) |
|
查看: 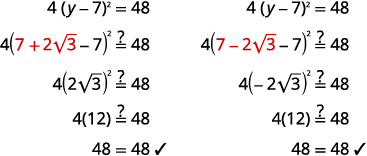
|
解决:\(3(a-3)^{2}=54\)。
- 回答
-
\(a=3+3 \sqrt{2}, \quad a=3-3 \sqrt{2}\)
解决:\(2(b+2)^{2}=80\)。
- 回答
-
\(b=-2+2 \sqrt{10}, \quad b=-2-2 \sqrt{10}\)
请记住,当我们取分数的平方根时,我们可以分别取分子和分母的平方根。
解决:\(\left(x-\frac{1}{3}\right)^{2}=\frac{5}{9}\)。
解决方案:
\(\left(x-\frac{1}{3}\right)^{2}=\frac{5}{9}\)
使用平方根属性。
\(x-\frac{1}{3}=\pm \sqrt{\frac{5}{9}}\)
将基数重写为平方根的分数。
\(x-\frac{1}{3}=\pm \frac{\sqrt{5}}{\sqrt{9}}\)
简化激进。
\(x-\frac{1}{3}=\pm \frac{\sqrt{5}}{3}\)
求解\(x\)。
\(x=\frac{1}{3} \pm \frac{\sqrt{5}}{3}\)
重写以显示两个解决方案。
\(x=\frac{1}{3}+\frac{\sqrt{5}}{3}, x=\frac{1}{3}-\frac{\sqrt{5}}{3}\)
查看:
我们把支票留给你。
解决:\(\left(x-\frac{1}{2}\right)^{2}=\frac{5}{4}\)。
- 回答
-
\(x=\frac{1}{2}+\frac{\sqrt{5}}{2}, x=\frac{1}{2}-\frac{\sqrt{5}}{2}\)
解决:\(\left(y+\frac{3}{4}\right)^{2}=\frac{7}{16}\)。
- 回答
-
\(y=-\frac{3}{4}+\frac{\sqrt{7}}{4}, y=-\frac{3}{4}-\frac{\sqrt{7}}{4}\)
我们将通过隔离二项式项来开始下一个示例的解。
解决:\(2(x-2)^{2}+3=57\)。
解决方案:
\(2(x-2)^{2}+3=57\)
\(3\)从两边减去以分离二项式项。
\(2(x-2)^{2}=54\)
将两边除以\(2\)。
\((x-2)^{2}=27\)
使用平方根属性。
\(x-2=\pm \sqrt{27}\)
简化激进。
\(x-2=\pm 3 \sqrt{3}\)
求解\(x\)。
\(x=2 \pm 3 \sqrt{3}\)
重写以显示两个解决方案。
\(x=2+3 \sqrt{3}, x=2-3 \sqrt{3}\)
查看:
我们把支票留给你。
解决:\(5(a-5)^{2}+4=104\)。
- 回答
-
\(a=5+2 \sqrt{5}, a=5-2 \sqrt{5}\)
解决:\(3(b+3)^{2}-8=88\)。
- 回答
-
\(b=-3+4 \sqrt{2}, \quad b=-3-4 \sqrt{2}\)
有时解是复数。
解决:\((2 x-3)^{2}=-12\)。
解决方案:
\((2 x-3)^{2}=-12\)
使用平方根属性。
\(2 x-3=\pm \sqrt{-12}\)
简化激进。
\(2 x-3=\pm 2 \sqrt{3} i\)
两\(3\)边都加上。
\(2 x=3 \pm 2 \sqrt{3} i\)
将两边除以\(2\)。
\(x=\frac{3 \pm 2 \sqrt{3 i}}{2}\)
以标准形式重写。
\(x=\frac{3}{2} \pm \frac{2 \sqrt{3} i}{2}\)
简化。
\(x=\frac{3}{2} \pm \sqrt{3} i\)
重写以显示两个解决方案。
\(x=\frac{3}{2}+\sqrt{3} i, x=\frac{3}{2}-\sqrt{3} i\)
查看:
我们把支票留给你。
解决:\((3 r+4)^{2}=-8\)。
- 回答
-
\(r=-\frac{4}{3}+\frac{2 \sqrt{2} i}{3}, r=-\frac{4}{3}-\frac{2 \sqrt{2} i}{3}\)
解决:\((2 t-8)^{2}=-10\)。
- 回答
-
\(t=4+\frac{\sqrt{10} i}{2}, t=4-\frac{\sqrt{10 i}}{2}\)
在接下来的两个例子中,方程的左边似乎不是这种形式\(a(x-h)^{2}\)。 但是它们是完美的正方三项式,所以我们会考虑把它们变成我们需要的形式。
解决:\(4 n^{2}+4 n+1=16\)。
解决方案:
我们注意到方程的左侧是一个完美的方形三项式。 我们将首先将其考虑在内。
| \(4 n^{2}+4 n+1=16\) | |
| 将完美的正方三项式分解出来。 | \((2 n+1)^{2}=16\) |
| 使用平方根属性。 | \(2 n+1=\pm \sqrt{16}\) |
| 简化激进。 | \(2 n+1=\pm 4\) |
| 求解\(n\)。 | \(2 n=-1 \pm 4\) |
| 将两边除以\(2\)。 | \(\begin{aligned} \frac{2 n}{2} &=\frac{-1 \pm 4}{2} \\ n &=\frac{-1 \pm 4}{2} \end{aligned}\) |
| 重写以显示两个解决方案。 | \(n=\frac{-1+4}{2}, n=\frac{-1-4}{2}\) |
| 简化每个方程。 | \(n=\frac{3}{2}, \quad n=-\frac{5}{2}\) |
|
查看: 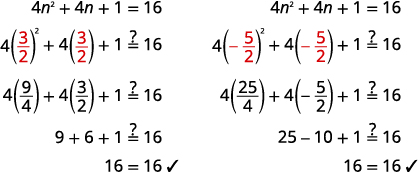
|
解决:\(9 m^{2}-12 m+4=25\)。
- 回答
-
\(m=\frac{7}{3}, \quad m=-1\)
解决:\(16 n^{2}+40 n+25=4\)。
- 回答
-
\(n=-\frac{3}{4}, \quad n=-\frac{7}{4}\)
访问此在线资源以获取更多指导和练习,使用平方根属性求解二次方程。
关键概念
- 平方根属性
- 如果\(x^{2}=k\)、则\(x=\sqrt{k}\)或\(x=-\sqrt{k}\)或\(x=\pm \sqrt{k}\)
- 分离二次项并将其系数设为一。
- 使用平方根属性。
- 简化激进。
- 检查解决方案。


