8.7: 求解激进方程
- Page ID
- 203983
在本节结束时,您将能够:
- 求解激进方程
- 用两个自由基求解激进方程
- 在应用中使用自由基
在开始之前,请参加这个准备测验。
- 简化:\((y−3)^{2}\)。
如果您错过了此问题,请查看示例 5.31。 - 解决:\(2x−5=0\)。
如果您错过了此问题,请查看示例 2.2。 - 解决\(n^{2}−6n+8=0\)。
如果您错过了此问题,请查看示例 6.45。
求解激进方程
在本节中,我们将求解在激进表达式的基数中具有变量的方程。 这种类型的方程称为激进方程。
定义\(\PageIndex{1}\)
其中变量位于激进表达式的基数中的方程称为激进方程。
像往常一样,在求解这些方程时,我们对方程的一侧所做的事情也必须对另一侧做。 一旦我们隔离了激进分子,我们的策略就是将方程的两边都提高到指数的次方。 这将消灭激进分子。
通过将两边提高到指数的幂来求解包含偶数指数的激进方程可能会引入代数解,而代数解不是原始激进方程的解。 再说一遍,我们称之为无关解,就像我们在求解有理方程时所做的那样。
在下一个例子中,我们将看到如何求解激进方程。 我们的策略是以\(n^{th}\)权力指数提高激进分子\(n\)为基础。 这将消灭激进分子。
对于\(a \geq 0,(\sqrt[n]{a})^{n}=a\)。
解决:\(\sqrt{5 n-4}-9=0\)。
解决方案:
| 步骤 1:分离方程一侧的自由基。 |
要隔离激进分子,\(9\)请在两边加入。 简化。 |
\(\begin{array}{c}{\sqrt{5 n-4}-9=0} \\ {\sqrt{5 n-4}-9\color{red}{+9}\color{black}{=}0\color{red}{+9}} \\ {\sqrt{5 n-4}=9}\end{array}\) |
| 步骤 2:将方程的两边提高到指数的乘方。 | 由于平方根的索引为\(2\),因此我们将两边进行平方。 | \((\sqrt{5 n-4})^{2}=(9)^{2}\) |
| 步骤 3:求解新方程。 | 记住,\((\sqrt{a})^{2}=a\)。 | \(\begin{aligned} 5 n-4 &=81 \\ 5 n &=85 \\ n &=17 \end{aligned}\) |
| 第 4 步:检查原始方程中的答案。 |
检查答案。 \(\begin{array}{r}{\sqrt{5 n-4}-9=0} \\ {\sqrt{5(\color{red}{17}\color{black}{)}-4}-9 \stackrel{?}{=} 0} \\ {\sqrt{85-4}-9 \stackrel{?}{=} 0} \\ {\sqrt{81}-9 \stackrel{?}{=} 0} \\ {9-9=0} \\ {0=0}\end{array}\) 解决办法是\(n=17\)。 |
解决:\(\sqrt{3 m+2}-5=0\)。
- 回答
-
\(m=\frac{23}{3}\)
解决:\(\sqrt{10 z+1}-2=0\)。
- 回答
-
\(z=\frac{3}{10}\)
用一个自由基求解一个激进方程
- 分离方程一侧的自由基。
- 将方程的两边提高到指数的幂次方。
- 求解新方程。
- 检查原始方程式中的答案。
当我们使用激进符号时,它表示主根或正根。 如果方程的基数为偶数索引等于负数,则该方程将没有解。
解决:\(\sqrt{9 k-2}+1=0\)。
解决方案:
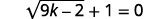 |
|
| 要隔离激进分子,\(1\)请将两边减去。 |  |
| 简化。 | 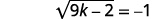 |
因为平方根等于负数,所以方程没有解。
解决:\(\sqrt{2 r-3}+5=0\)。
- 回答
-
没有解决办法
解决:\(\sqrt{7 s-3}+2=0\)。
- 回答
-
没有解决办法
如果具有平方根的方程的一边是二项式,则我们在求方时使用二项式方块的乘积图案。
定义\(\PageIndex{2}\)
二项式方块
\(\begin{array}{l}{(a+b)^{2}=a^{2}+2 a b+b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}\)
别忘了中间学期!
解决:\(\sqrt{p-1}+1=p\)。
解决方案:
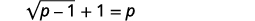 |
|
| 要隔离激进分子,请\(1\)从两边减去。 | 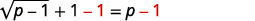 |
| 简化。 | 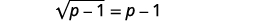 |
| 对方程的两边进行平方。 | 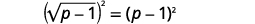 |
| 使用右侧的二项式正方形乘积图案进行简化,然后求解新方程。 | 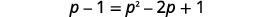 |
| 它是一个二次方程,所以在一边求零。 | 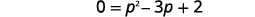 |
| 将右侧考虑在内。 | 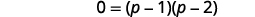 |
| 使用 “零积分” 属性。 | 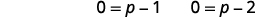 |
| 求解每个方程。 | 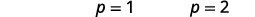 |
| 查看答案。 | |
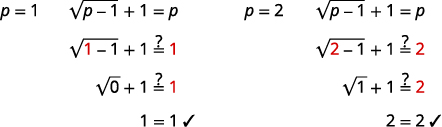 |
解决方案是\(p=1, p=2\)。
解决:\(\sqrt{x-2}+2=x\)。
- 回答
-
\(x=2, x=3\)
解决:\(\sqrt{y-5}+5=y\)。
- 回答
-
\(y=5, y=6\)
当激进的索引为时\(3\),我们将两边立方体以移除部首。
\((\sqrt[3]{a})^{3}=a\)
解决:\(\sqrt[3]{5 x+1}+8=4\)。
解决方案:
| \(\sqrt[3]{5 x+1}+8=4\) | |
| 要隔离激进分子,请\(8\)从两边减去。 | \(\sqrt[3]{5 x+1}=-4\) |
| 将方程的两边立方块。 | \((\sqrt[3]{5 x+1})^{3}=(-4)^{3}\) |
| 简化。 | \(5 x+1=-64\) |
| 求解方程。 | \(5 x=-65\) |
| \(x=-13\) | |
| 检查答案。 | |
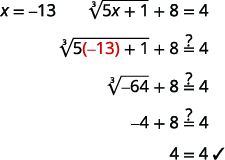 |
|
| 解决办法是\(x=-13\)。 |
解决:\( \sqrt[3]{4 x-3}+8=5\)
- 回答
-
\(x=-6\)
解决:\(\sqrt[3]{6 x-10}+1=-3\)
- 回答
-
\(x=-9\)
有时,方程会包含有理指数,而不是激进。 我们使用与求解激进时相同的方法来求解方程。 我们将方程的每一边提高到有理指数分母的幂次方。 因为\(\left(a^{m}\right)^{^{n}}=a^{m \cdot n}\),举个例子,
\(\left(x^{\frac{1}{2}}\right)^{2}=x,\left(x^{\frac{1}{3}}\right)^{3}=x\)
记住,\(x^{\frac{1}{2}}=\sqrt{x}\)和\(x^{\frac{1}{3}}=\sqrt[3]{x}\)。
解决:\((3 x-2)^{\frac{1}{4}}+3=5\)。
解决方案:
| \((3 x-2)^{\frac{1}{4}}+3=5\) | |
| 要用有理指数分离该项,请\(3\)从两边减去。 | \((3 x-2)^{\frac{1}{4}}=2\) |
| 将方程的每一边提高到第四次方。 | \(\left((3 x-2)^{\frac{1}{4}}\right)^{4}=(2)^{4}\) |
| 简化。 | \(3 x-2=16\) |
| 求解方程。 | \(3x=18\) |
| \(x=6\) | |
| 检查答案。 | |
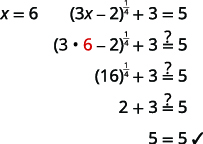 |
|
| 解决办法是\(x=6\)。 |
解决:\((9 x+9)^{\frac{1}{4}}-2=1\)
- 回答
-
\(x=8\)
解决:\((4 x-8)^{\frac{1}{4}}+5=7\)
- 回答
-
\(x=6\)
有时,激进方程的解会产生两个代数解,但其中一个可能是无关的解!
解决:\(\sqrt{r+4}-r+2=0\)。
解决方案:
| \(\sqrt{r+4}-r+2=0\) | |
| 隔离激进分子。 | \(\sqrt{r+4}=r-2\) |
| 对方程的两边进行平方。 | \((\sqrt{r+4})^{2}=(r-2)^{2}\) |
| 简化然后求解方程。 | \(r+4=r^{2}-4 r+4\) |
| 如果是二次方程,则在一侧取零。 | \(0=r^{2}-5 r\) |
| 将右侧考虑在内。 | \(0=r(r-5)\) |
| 使用 “零积分” 属性。 | \(0=r \quad 0=r-5\) |
| 求解方程。 | \(r=0 \quad r=5\) |
| 检查你的答案。 | |
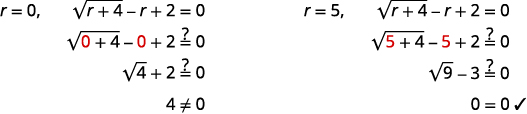 |
解决办法是\(r=5\)。 |
| \(r=0\)是一个极端的解决方案。 |
解决:\(\sqrt{m+9}-m+3=0\)
- 回答
-
\(m=7\)
解决:\(\sqrt{n+1}-n+1=0\)。
- 回答
-
\(n=3\)
当激进前面有一个系数时,我们也必须将其提高到指数的幂次方。
解决:\(3 \sqrt{3 x-5}-8=4\)。
解决方案:
| \(3 \sqrt{3 x-5}-8=4\) | |
| 分离激进术语。 | \(3 \sqrt{3 x-5}=12\) |
| 通过将两边除以来隔离激进分子\(3\)。 | \(\sqrt{3 x-5}=4\) |
| 对方程的两边进行平方。 | \((\sqrt{3 x-5})^{2}=(4)^{2}\) |
| 简化,然后求解新方程。 | \(3 x-5=16\) |
| \(3x=21\) | |
| 求解方程。 | \(x=7\) |
| 检查答案。 | |
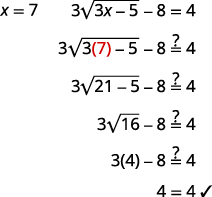 |
|
| 解决办法是\(x=7\)。 |
解决:\(2 \sqrt{4 a+4}-16=16\)。
- 回答
-
\(a=63\)
解决:\(3 \sqrt{2 b+3}-25=50\)
- 回答
-
\(b=311\)
用两个自由基求解激进方程
如果激进方程有两个自由基,我们首先隔离其中一个。 通常最简单的方法是先隔离更复杂的激进分子。
在下一个例子中,当一个激进分子被隔离时,第二个激进分子也被隔离。
解决:\(\sqrt[3]{4 x-3}=\sqrt[3]{3 x+2}\)。
解决方案:
激进的术语是孤立的。
\(\sqrt[3]{4 x-3}=\sqrt[3]{3 x+2}\)
由于索引为\(3\),因此方程的两边均为立方体。
\((\sqrt[3]{4 x-3})^{3}=(\sqrt[3]{3 x+2})^{3}\)
简化,然后求解新方程。
\(\begin{aligned} 4 x-3 &=3 x+2 \\ x-3 &=2 \\ x &=5 \end{aligned}\)
解决办法是\(x=5\)。
检查答案。
我们留给你出示那\(5\)张支票!
解决:\(\sqrt[3]{5 x-4}=\sqrt[3]{2 x+5}\)。
- 回答
-
\(x=3\)
解决:\(\sqrt[3]{7 x+1}=\sqrt[3]{2 x-5}\)。
- 回答
-
\(x=-\frac{6}{5}\)
有时候,在将方程的两边都提高为幂之后,激进内部还有一个变量。 发生这种情况时,我们重复程序的第 1 步和第 2 步。 我们将激进分离出来,然后将方程的两边再次提高到指数的幂次。
解决:\(\sqrt{m}+1=\sqrt{m+9}\)。
解决方案:
| 步骤 1:在方程的一侧分离出其中一个基项。 | 右翼的激进分子是孤立的。 | \(\sqrt{m}+1=\sqrt{m+9}\) |
| 步骤 2:将方程的两边提高到指数的乘方。 |
我们把两边都弄平。 简化——乘法时要非常小心! |
\((\sqrt{m}+1)^{2}=(\sqrt{m+9})^{2}\) |
|
第 3 步:还有其他激进分子吗? 如果是,请再次重复步骤 1 和步骤 2。 如果不是,则求解新方程。 |
方程式中还有一个激进分子。 因此,我们必须重复前面的步骤。 分离激进术语。 在这里,我们可以通过将双方除以来轻松地隔离激进分子\(2\)。 两边都是正方形。 |
\(\begin{aligned} m+2 \sqrt{m}+1 &=m+9 \\ 2 \sqrt{m} &=8 \\ \sqrt{m} &=4 \\(\sqrt{m})^{2} &=(4)^{2} \\ m &=16 \end{aligned}\) |
| 第 4 步:检查原始方程中的答案。 |
\(\begin{aligned}\sqrt{m}+1&=\sqrt{m+9} \\ \sqrt{\color{red}{16}}\color{black}{+}1& \stackrel{?}{=} \sqrt{\color{red}{16}\color{black}{+}9} \\ 4+1& \stackrel{?}{=} 5 \\ 5&=5\end{aligned}\) 解决办法是\(m=16\)。 |
解决:\(3-\sqrt{x}=\sqrt{x-3}\)。
- 回答
-
\(x=4\)
解决:\(\sqrt{x}+2=\sqrt{x+16}\)。
- 回答
-
\(x=9\)
我们在这里总结一下步骤。 我们已经调整了之前的步骤,在方程中包含了多个激进方程。此过程现在适用于任何激进方程。
求解激进方程
- 在方程的一侧分离出其中一个激进项。
- 将方程的两边提高到指数的幂次方。
- 还有其他激进分子吗?
如果是,请再次重复步骤 1 和步骤 2。
如果不是,则求解新方程。 - 检查原始方程式中的答案。
在下一个示例中对二项式求方时要小心。 记住\((a+b)^{2}=a^{2}+2 a b+b^{2}\)或中的模式\((a-b)^{2}=a^{2}-2 a b+b^{2}\)。
解决:\(\sqrt{q-2}+3=\sqrt{4 q+1}\)。
解决方案:
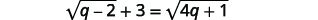 |
|
| 右翼的激进分子是孤立的。 两边都是正方形。 | 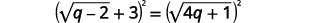 |
| 简化。 | 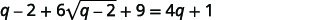 |
| 方程中还有一个激进,所以我们必须重复前面的步骤。 隔离激进分子。 | 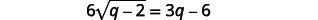 |
| 两边都是正方形。 将双方分开无济于事\(6\)。 记得把\(6\)和都对齐\(\sqrt{q-2}\)。 | 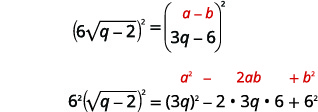 |
| 简化,然后求解新方程。 | 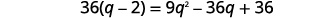 |
| 分发。 | 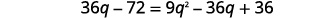 |
| 它是一个二次方程,所以在一边求零。 | 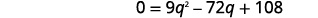 |
| 将右侧考虑在内。 | 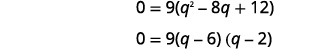 |
| 使用 “零积分” 属性。 | 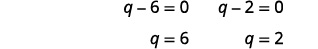 |
| 支票留给你了。 | 解决方案是\(q=6\)和\(q=2\)。 |
解决:\(\sqrt{x-1}+2=\sqrt{2 x+6}\)
- 回答
-
\(x=5\)
解决:\(\sqrt{x}+2=\sqrt{3 x+4}\)
- 回答
-
\(x=0 x=4\)
在应用程序中使用自由基
随着大学课程的进展,你会遇到包含许多学科激进分子的公式。 我们将稍微修改几何应用程序的问题解决策略,以便为我们提供一个使用任何学科公式求解应用程序的计划。
对带有公式的应用程序使用问题解决策略
- 阅读问题并确保所有文字和想法都被理解。 在适当的时候,画一个图形并用给定的信息贴上标签。
- 确定我们在寻找什么。
- 通过选择一个变量来表示我们要找的东西来@@ 命名它。
- 通过编写适合情况的公式或模型将其@@ 转换为方程。 在给定的信息中替换。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
自由基的一种应用与重力对坠落物体的影响有关。 该公式使我们能够确定坠落的物体需要多长时间才能撞到地面。
定义\(\PageIndex{2}\)
坠落物体
在地球上,如果物体从\(h\)英尺的高度掉落,则使用公式得出到达地面所需的时间(以秒为单位)
\(t=\frac{\sqrt{h}}{4}\)
例如,如果一个物体从\(64\)英尺的高度掉落,我们可以通过代\(h=64\)入公式来计算到达地面所需的时间。
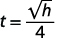 |
|
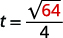 |
|
| 取的平方根\(64\)。 | 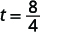 |
| 简化分数。 | 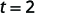 |
从\(64\)英尺高度掉落的物体需要\(2\)几秒钟才能到达地面。
玛丽莎从河上的一座桥\(400\)脚下掉下了太阳镜。 使用公式计算\(t=\frac{\sqrt{h}}{4}\)太阳镜到达河里花了多少秒钟。
解决方案:
| 第 1 步:阅读问题。 | |
| 第 2 步:确定我们在寻找什么。 | 太阳镜到达河里所花费的时间。 |
| 第 3 步:说出我们正在寻找的内容。 | 让 (t=\) 时间吧。 |
| 第 4 步:通过编写相应的公式将其转换为方程。 在给定的信息中替换。 | 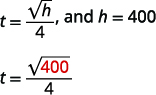 |
| 步骤 5:求解方程。 |  |
 |
|
| 第 6 步:检查问题中的答案并确保答案合理。 | 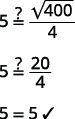 |
| \(5\)秒看起来像是合理的时间长度吗? | 是的。 |
| 步骤 7:回答方程式。 | 太阳镜需要\(5\)几秒钟才能到达河边。 |
一架直升机从\(1,296\)英尺高处投下了一个救援包。 使用公式计算\(t=\frac{\sqrt{h}}{4}\)包裹到达地面花了多少秒钟。
- 回答
-
\(9\)秒
洗窗器从人行道上方的平台\(196\)脚下掉了一把刮刀。 使用该公式计算\(t=\frac{\sqrt{h}}{4}\)刮刀到达人行道花了多少秒钟。
- 回答
-
\(3.5\)秒
调查车祸的警官测量人行道上防滑痕迹的长度。 然后,他们使用平方根来确定汽车在刹车前行驶的速度,以英里/小时为单位。
定义\(\PageIndex{3}\)
汽车的防滑痕迹和速度
如果防滑痕迹的长度为\(d\)英尺\(s\),则可以使用以下公式得出刹车前汽车的速度
\(s=\sqrt{24 d}\)
车祸发生后,一辆汽车的防滑痕迹测量\(190\)英尺。 在施加制动之前,使用该公式\(s=\sqrt{24d}\)找出汽车的速度。 将答案四舍五入到最接近的十分之一。
解决方案:
| 第 1 步:阅读问题。 | |
| 第 2 步:确定我们在寻找什么。 | 汽车的速度。 |
| 第 3 步:说出我们要找的内容。 | 让速度\(s=\)加快。 |
| 第 4 步:通过编写相应的公式将其转换为方程。 在给定的信息中替换。 | 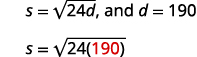 |
| 步骤 5:求解方程。 | 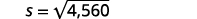 |
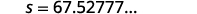 |
|
| 四舍\(1\)五入到小数位。 |  |
 |
|
| 刹车前汽车的速度为每小时\(67.5\)英里数。 |
事故调查员测量了汽车的防滑痕迹。 防滑痕迹的长度为\(76\)英尺。 在施加制动之前,使用该公式\(s=\sqrt{24d}\)找出汽车的速度。 将答案四舍五入到最接近的十分之一。
- 回答
-
\(42.7\)英尺
发生事故的车辆的防滑痕迹长达一\(122\)英尺。 在施加制动之前,使用该公式\(s=\sqrt{24d}\)找出车辆的速度。 将答案四舍五入到最接近的十分之一。
- 回答
-
\(54.1\)英尺
访问这些在线资源,获取求解激进方程的更多指导和练习。
- 求解涉及单个自由基的方程
- 用自由基和有理指数求解方程
- 求解激进方程
- 求解激进方程
- 激进方程应用
关键概念
- 二项式方块
\(\begin{array}{l}{(a+b)^{2}=a^{2}+2 a b+b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}\) - 求解激进方程
- 在方程的一侧分离出其中一个激进项。
- 将方程的两边提高到指数的幂次方。
- 还有其他激进分子吗?
如果是,请再次重复步骤 1 和步骤 2。
如果不是,则求解新方程。 - 检查原始方程式中的答案。
- 使用公式的应用程序的问题解决策略
- 阅读问题并确保所有文字和想法都被理解。 在适当的时候,画一个图形并用给定的信息贴上标签。
- 确定我们在寻找什么。
- 通过选择一个变量来表示我们要找的东西来命名它。
- 通过编写适合情况的公式或模型将其转换为方程。 在给定的信息中替换。
- 使用良好的代数技巧求解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子回答问题。
- 坠落物体
- 在地球上,如果物体从\(h\)英尺的高度掉落,则使用公式得出到达地面所需的时间(以秒为单位)\(t=\frac{\sqrt{h}}{4}\)。
- 汽车的防滑痕迹和速度
- 如果防滑痕迹的长度为\(d\)英尺\(s\),则可以使用公式得出刹车前汽车的速度\(s=\sqrt{24d}\)。
词汇表
- 激进方程
- 其中变量位于激进表达式的基数中的方程称为激进方程。


