7.2: 有理表达式的乘法和除法
- Page ID
- 204272
在本节结束时,您将能够:
- 确定未定义有理表达式的值
- 简化有理表达式
- 乘以有理表达式
- 除以有理表达式
- 有理函数的乘法和除法
在@@
我们之前回顾了分数的特性及其运算。 我们引入了有理数,它们只是分数,其中分子和分母是整数。 在本章中,我们将研究分子和分母是多项式的分数。 我们称这种表达方式为理性表达。
有理表达式是形式的\(\dfrac{p}{q}\), where \(p\) 表达式,\(q\) 是多项式和\(q\neq 0\).
以下是一些有理表达式的例子:
\[−\dfrac{24}{56} \qquad \dfrac{5x}{12y} \qquad \dfrac{4x+1}{x^2−9} \qquad \dfrac{4x^2+3x−1}{2x−8}\nonumber\]
请注意,上面列出的第一个有理表达式只是一个分数。\(−\dfrac{24}{56}\) 由于常量是零度的多项式,因此只要分母不为零,两个常量的比率就是有理表达式。
我们将使用与分数相同的有理表达式进行运算。 我们将对它们进行简化、加、减、乘、除并在应用程序中使用。
确定未定义有理表达式的值
如果分母为零,则有理表达式未定义。 有理表达式的分子可能为 0,但不是分母。
当我们处理数字分数时,很容易避免除以零,因为我们可以看到分母中的数字。 为了避免在有理表达式中除以零,我们决不能允许将使分母变为零的变量的值。
因此,在我们开始使用有理表达式进行任何运算之前,我们首先对其进行检查以找到将使分母为零的值。 这样,例如,当我们求解有理方程时,我们就会知道我们找到的代数解是否允许。
- 将分母设置为零。
- 求解方程。
确定每个有理表达式未定义的值:
a.\(\dfrac{8a^2b}{3c}\) b.\(\dfrac{4b−3}{2b+5}\) c\(\dfrac{x+4}{x^2+5x+6}\).
解决方案
当分母为零时,表达式将未定义。
一个。
\(\begin{array} {ll} &\dfrac{8a^2b}{3c} \\ \begin{array} {l} \text{Set the denominator equal to zero and solve} \\ \text{for the variable.} \end{array} &3c=0 \\ &c=0 \\ &\dfrac{8a^2b}{3c}\text{ is undefined for }c=0 \end{array} \)
b。
\(\begin{array} {ll} &\dfrac{4b-3}{2b+5} \\ \begin{array} {l} \text{Set the denominator equal to zero and solve} \\ \text{for the variable.} \end{array} &2b+5=0 \\ &2b=-5 \\ &b=-\dfrac{5}{2} \\ & \\ &\dfrac{4b-3}{2b+5} \text{ is undefined for }b=-\dfrac{5}{2} \end{array} \)
c。
\(\begin{array} {ll} &\dfrac{x+4}{x^2 + 5x + 6} \\ \begin{array} {l} \text{Set the denominator equal to zero and solve } \\ \text{for the variable.} \end{array} &x^2+5x+6=0 \\ &(x+2)(x+3)=0 \\ &x+2=0\text{ or }x+3=0 \\ &x=-2\text{ or }x=-3 \\ & \\ &\dfrac{x+4}{x^2+5x+6}\text{ is undefined for }x=-2\text{ or }x=-3 \end{array} \)
确定每个有理表达式未定义的值。
a.\(\dfrac{3y^2}{8x}\) b.\(\dfrac{8n−5}{3n+1}\) c.\(\dfrac{a+10}{a^2+4a+3}\)
- 回答
-
a.\(x=0\)
b.\(n=−\dfrac{1}{3}\)
c.\(a=−1,a=−3\)
确定每个有理表达式未定义的值。
a.\(\dfrac{4p}{5q}\) b.\(\dfrac{y−1}{3y+2}\) c.\(\dfrac{m−5}{m^2+m−6}\)
- 回答
-
a.\(q=0\)
b.\(y=−\dfrac{2}{3}\)
c.\(m=2,m=−3\)
简化有理表达式
如果分数的分子和分母中除了 1 之外没有其他公共因子,则认为该分数是简化的。 同样,简化的有理表达式的分子和分母中除了 1 之外没有其他共同因子。
如果有理表达式的分子和分母中没有共同的因子,则认为有理表达式是简化的。
例如,
\[ \begin{array} {l} \dfrac{x+2}{x+3} \text{ is simplified because there are no common factors of } x+2 \text{ and }x+3. \\ \dfrac{2x}{3x} \text{ is not simplified because x is a common factor of }2x\text{ and }3x. \\ \end{array} \nonumber\]
我们使用等效分数属性来简化数字分数。 我们在此重述一下,因为我们还将使用它来简化有理表达式。
如果\(a\)\(b\)、和\(c\)是数字,其中\(b\neq 0,c\neq 0,\)
\[\text {then } \dfrac{a}{b}=\dfrac{a·c}{b·c} \text{ and } \dfrac{a·c}{b·c}=\dfrac{a}{b}\nonumber\]
请注意,在等效分数属性中,明确禁止使用会使分母为零的值。 我们看得\(b\neq 0,c\neq 0\)很清楚。
为了简化有理表达式,我们首先以因子形式写出分子和分母。 然后我们使用等效分数属性移除常见因子。
在删除常见因素时要非常小心。 将因子乘以制成产品。 您可以从产品中移除因子。 您不能从总和中删除一个术语。

从\(\dfrac{x+5}{x}\)中删除 “\(x\)s” 就像取消分数中的 “\(2\)s” 一样\(\dfrac{2+5}{2}!\)
如何简化理性表达
简化:\(\dfrac{x^2+5x+6}{x^2+8x+12}\)
解决方案
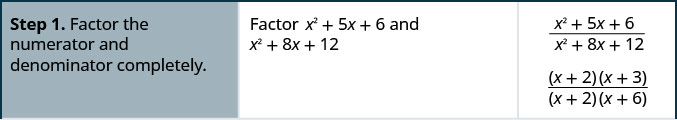

简化:\(\dfrac{x^2−x−2}{x^2−3x+2}\)。
- 回答
-
\(\dfrac{x+1}{x−1},x\neq 2,x\neq 1\)
简化:\(\dfrac{x^2−3x−10}{x^2+x−2}\)。
- 回答
-
\(\dfrac{x−5}{x−1},x\neq −2,x\neq 1\)
现在,我们总结了简化有理表达式时应遵循的步骤。
- 将分子和分母完全分解。
- 通过划分常见因素进行简化。
通常,我们将简化的理性表达以因子形式保留。 这样,就可以很容易地检查我们是否消除了所有常见因素。
在以下示例中,我们将使用我们学到的方法对分子和分母中的多项式进行分解。
每次我们写一个有理的表达式时,我们都应该声明不允许使用会使分母为零的值。 但是,为了让我们专注于手头的工作,我们将省略将其写在示例中。
简化:\(\dfrac{3a^2−12ab+12b^2}{6a^2−24b^2}\)。
解决方案
\(\begin{array} {ll} &\dfrac{3a^2−12ab+12b^2}{6a^2−24b^2} \\ & \\ & \\ \begin{array} {l} \text{Factor the numerator and denominator,} \\ \text{first factoring out the GCF.} \end{array} &\dfrac{3(a^2−4ab+4b^2)}{6(a^2−4b^2)} \\ & \\ &\dfrac{3(a−2b)(a−2b)}{6(a+2b)(a−2b)} \\ & \\ \text{Remove the common factors of }a−2b\text{ and }3. &\dfrac{\cancel{3}(a−2b)\cancel{(a−2b)}}{\cancel{3}·2(a+2b)\cancel{(a−2b)}} \\ &\dfrac{a−2b}{2(a+2b)} \end{array} \)
简化:\(\dfrac{2x^2−12xy+18y^2}{3x^2−27y^2}\)。
- 回答
-
\(\dfrac{2(x−3y)}{3(x+3y)}\)
简化:\(\dfrac{5x^2−30xy+25y^2}{2x^2−50y^2}\)。
- 回答
-
\(\dfrac{5(x−y)}{2(x+5y)}\)
现在我们将看到如何简化其分子和分母具有相反因子的有理表达式。 我们之前引入了相反的表示法:\(a\)是\(−a\) and 的对立面\(−a=−1·a\)。
比如说,数值分数\(\dfrac{7}{−7}\)简化为\(−1\)。 我们还认识到,分子和分母是相反的。
分子\(\dfrac{a}{−a}\)和分母相反的分数也简化为\(−1\)。
\[\begin{array} {ll} \text{Let’s look at the expression }b−a. &b−a \\ \text{Rewrite.} &−a+b \\ \text{Factor out }–1. &−1(a−b) \nonumber\end{array} \]
这告诉我们\(b−a\)情况恰恰相反\(a−b\)。
总的来说,我们可以写与 as 相反\(a−b\)的内容\(b−a\)。 因此,理性表达式\(\dfrac{a−b}{b−a}\)简化为\(−1\)。
恰恰相反\(b−a\)。\(a−b\)
\[\dfrac{a−b}{b−a}=−1 \quad a\neq b\nonumber\]
表达式及其相反的除法为\(−1\)。
我们将使用此属性来简化分子和分母中包含对立面的有理表达式。 注意不要把\(a+b\)和\(b+a\)当作对立面来对待。 此外,回想一下,顺序并不重要\(a+b=b+a\)。 所以如果\(a\neq −b\),那么\(\dfrac{a+b}{b+a}=1\)。
简化:\(\dfrac{x^2−4x−32}{64−x^2}\)
解决方案
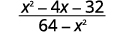 |
|
| 将分子和分母分数分数除外。 | 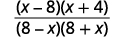 |
| 认识相反的因素。 | 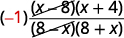 |
| 简化。 | 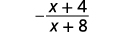 |
简化:\(\dfrac{x^2−4x−5}{25−x^2}\)
- 回答
-
\(−\dfrac{x+1}{x+5}\)
简化:\(\dfrac{x^2+x−2}{1−x^2}\)。
- 回答
-
\(−\dfrac{x+2}{x+1}\)
乘以有理表达式
为了乘以有理表达式,我们就像使用数值分数一样。 我们乘以分子,然后乘以分母。 然后,如果有任何常见因素,我们将其删除以简化结果。
如果\(p\)、\(q\)\(r\)、和\(s\)是多项式\(q\neq 0\),其中、\(s\neq 0\)、那么
\[\dfrac{p}{q}·\dfrac{r}{s}=\dfrac{pr}{qs}\nonumber\]
要乘以有理表达式,请将分子相乘并乘以分母。
请记住,在本章中,我们将假设所有使分母为零的数值都被排除在外。 我们不会为每个有理表达式写出限制,但请记住,分母永远不能为零。 因此,在下一个示例中\(x\neq 0\),\(x\neq 3\)、和\(x\neq 4.\)
简化:\(\dfrac{2x}{x^2−7x+12}·\dfrac{x^2−9}{6x^2}\)。
解决方案
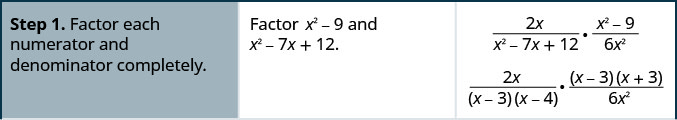


简化:\(\dfrac{5x}{x^2+5x+6}·\dfrac{x^2−4}{10x}\)。
- 回答
-
\(\dfrac{x−2}{2(x+3)}\)
简化:\(\dfrac{9x^2}{x^2+11x+30}·\dfrac{x^2−36}{3x^2}\)。
- 回答
-
\(\dfrac{3(x−6)}{x+5}\)
- 将每个分子和分母完全分解。
- 将分子和分母相乘。
- 通过划分常见因素进行简化。
乘以:\(\dfrac{3a^2−8a−3}{a^2−25}·\dfrac{a^2+10a+25}{3a^2−14a−5}\)。
解决方案
\(\begin{array} {ll} &\dfrac{3a^2−8a−3}{a^2−25}·\dfrac{a^2+10a+25}{3a^2−14a−5} \\ & \\ \begin{array} {ll} \text{Factor the numerators and denominators} \\ \text{and then multiply.} \end{array} &\dfrac{(3a+1)(a−3)(a+5)(a+5)}{(a−5)(a+5)(3a+1)(a−5)} \\ & \\ \begin{array} {l} \text{Simplify by dividing out} \\ \text{common factors.} \end{array} &\dfrac{\cancel{(3a+1)}(a−3)\cancel{(a+5)}(a+5)}{(a−5)\cancel{(a+5)}\cancel{(3a+1)}(a−5)} \\ & \\ \text{Simplify.} &\dfrac{(a−3)(a+5)}{(a−5)(a−5)} \\ & \\ \text{Rewrite }(a−5)(a−5)\text{ using an exponent.} &\dfrac{(a−3)(a+5)}{(a−5)^2} \end{array}\)
简化:\(\dfrac{2x^2+5x−12}{x^2−16}·\dfrac{x^2−8x+16}{2x^2−13x+15}\)。
- 回答
-
\(\dfrac{x−4}{x−5}\)
简化:\(\dfrac{4b^2+7b−2}{1−b^2}·\dfrac{b^2−2b+1}{4b^2+15b−4}\)。
- 回答
-
\(−\dfrac{(b+2)(b−1)}{(1+b)(b+4)}\)
划分有理表达式
就像我们对数值分数所做的那样,要除以有理表达式,我们将第一个分数乘以第二个分数的倒数。
如果\(p\)、\(q\)\(r\)、和\(s\)是多项式\(q\neq 0\),其中、\(r\neq 0\)、\(s\neq 0\)、那么
\[\dfrac{p}{q}÷\dfrac{r}{s}=\dfrac{p}{q}·\dfrac{s}{r}\nonumber\]
要除以有理表达式,请将第一个分数乘以第二个分数的倒数。
一旦我们将除法重写为第一个表达式乘以第二个表达式的倒数,然后我们将所有表达式分解并寻找共同因子。
除以:\(\dfrac{p^3+q^3}{2p^2+2pq+2q^2}÷\dfrac{p^2−q^2}{6}\)。
解决方案




简化:\(\dfrac{x^3−8}{3x^2−6x+12}÷\dfrac{x^2-4}{6}\)。
- 回答
-
\(\dfrac{2(x^2+2x+4)}{(x+2)(x^2−2x+4)}\)
简化:\(\dfrac{2z^2}{z^2−1}÷\dfrac{z^3−z^2+z}{z^3+1}\)。
- 回答
-
\(\dfrac{2z}{z−1}\)
- 将除法重写为第一个有理表达式的乘积和第二个有理表达式的倒数的乘积。
- 将分子和分母完全分解。
- 将分子和分母相乘。
- 通过划分常见因素进行简化。
回想一下 Use the Language of Algebra 中的复数分数是分数,分母或两者兼而有之。 另外,请记住,分数条表示除法。 复数分数是写两个分数除法的另一种方式。
除以:\(\dfrac{\dfrac{6x^2−7x+2}{4x−8}}{\dfrac{2x^2−7x+3}{x^2−5x+6}}\)。
解决方案
\(\begin{array} {ll} &\dfrac{\dfrac{6x^2−7x+2}{4x−8}}{\dfrac{2x^2−7x+3}{x^2−5x+6}} \\ & \\ \text{Rewrite with a division sign.} &\dfrac{6x^2−7x+2}{4x−8}÷\dfrac{2x^2−7x+3}{x^2−5x+6} \\ & \\ \begin{array} {l} \text{Rewrite as product of first times reciprocal} \\ \text{of second.} \end{array} &\dfrac{6x^2−7x+2}{4x−8}·\dfrac{x^2−5x+6}{2x^2−7x+3} \\ & \\ \begin{array} {l} \text{Factor the numerators and the} \\ \text{denominators, and then multiply.} \end{array} &\dfrac{(2x−1)(3x−2)(x−2)(x−3)}{4(x−2)(2x−1)(x−3)} \\ & \\ \text{Simplify by dividing out common factors.} &\dfrac{\cancel{(2x−1)}(3x−2)\cancel{(x−2)}\cancel{(x−3)}}{4\cancel{(x−2)}\cancel{(2x−1)}\cancel{(x−3)}} \\ \text{Simplify.} &\dfrac{3x−2}{4} \end{array}\)
简化:\(\dfrac{\dfrac{3x^2+7x+2}{4x+24}}{\dfrac{3x^2−14x−5}{x^2+x−30}}\)。
- 回答
-
\(\dfrac{x+2}{4}\)
简化:\(\dfrac{\dfrac{y^2−36}{2y^2+11y−6}}{\dfrac{2y^2−2y−60}{8y−4}}\)。
- 回答
-
\(\dfrac{2}{y+5}\)
如果我们有两个以上的有理表达式可供使用,我们仍然遵循相同的程序。 第一步是将任何除法重写为乘以倒数。 然后,我们进行分数并乘以。
执行指示的操作:\(\dfrac{3x−6}{4x−4}·\dfrac{x^2+2x−3}{x^2−3x−10}÷\dfrac{2x+12}{8x+16}\)。
解决方案
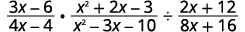 |
|
| 将除法重写为 乘以倒数。 |
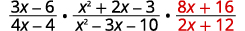 |
| 将分子和分母计算在内。 | 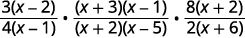 |
| 将分数相乘。 在移除常见因子时 ,将常数放在最前面会有所帮助。 |
|
| 通过划分常见因素进行简化。 | 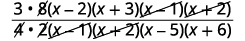 |
| 简化。 | 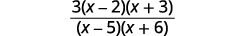 |
执行指示的操作:\(\dfrac{4m+4}{3m−15}·\dfrac{m^2−3m−10}{m^2−4m−32}÷\dfrac{12m−36}{6m−48}\)。
- 回答
-
\(\dfrac{2(m+1)(m+2)}{3(m+4)(m−3)}\)
执行指示的操作:\(\dfrac{2n^2+10n}{n−1}÷\dfrac{n^2+10n+24}{n^2+8n−9}·\dfrac{n+4}{8n^2+12n}\)。
- 回答
-
\(\dfrac{(n+5)(n+9)}{2(n+6)(2n+3)}\)
有理函数的乘法和除法
我们在本节开始时指出,有理表达式是形式的表达式\(\dfrac{p}{q}\),其中 p 和 q 是多项式,\(q\neq 0\). 同样,我们将有理函数定义为一种形式的函数,\(R(x)=\dfrac{p(x)}{q(x)}\)其中\(p(x)\)和\(q(x)\)是多项式函数,不是零。\(q(x)\)
有理函数是以下形式的函数
\[R(x)=\dfrac{p(x)}{q(x)}\nonumber\]
其中\(p(x)\)和\(q(x)\)是多项式函数\(q(x)\),不为零。
除了那些会导致除以零的值外,有理函数的域都是实数。 我们必须消除任何创造价值观的价值\(q(x)=0\)。
- 将分母设置为零。
- 求解方程。
- 域是所有实数,不包括步骤 2 中找到的值。
找到的域\(R(x)=\dfrac{2x^2−14x}{4x^2−16x−48}\)。
解决方案
除那些使分母为零的值外,该域将全部为实数。 我们将把分母设置为零,求解该方程,然后将这些值从域中排除。
\(\begin{array} {ll} \text{Set the denominator to zero.} &4x^2−16x−48=0 \\ \text{Factor, first factor out the GCF.} &4(x^2−4x−12)=0 \\ &4(x−6)(x+2)=0 \\ \text{Use the Zero Product Property.} &4\neq 0\quad x−6=0\quad x+2=0 \\ \text{Solve.} &\hspace{24mm}x=6\qquad x=−2 \\ &\text{The domain of }R(x)\text{ is all real numbers} \\ &\text{where }x\neq 6\text{ and }x\neq −2 \end{array}\)。
找到的域\(R(x)=\dfrac{2x^2−10x}{4x^2−16x−20}\)。
- 回答
-
的域\(R(x)\)是所有实数,其中 an\(x\neq 5\) d\(x\neq −1\)。
找到的域\(R(x)=\dfrac{4x^2−16x}{8x^2−16x−64}\)。
- 回答
-
的域\(R(x)\)是所有实数,其中 an\(x\neq 4\) d\(x\neq −2\)。
为了乘以有理函数,我们使用与乘有理表达式相同的方法将方程右侧生成的有理表达式相乘。
找出\(R(x)=f(x)·g(x)\)位置\(f(x)=\dfrac{2x−6}{x^2−8x+15}\)和\(g(x)=\dfrac{x^2−25}{2x+10}\).
解决方案
\(\begin{array} {ll} &R(x)=f(x)·g(x) \\ & \\ &R(x)=\dfrac{2x−6}{x^2−8x+15}·\dfrac{x^2−25}{2x+10} \\ & \\ \text{Factor each numerator and denominator.} &R(x)=\dfrac{2(x−3)}{(x−3)(x−5)}·\dfrac{(x−5)(x+5)}{2(x+5)} \\ & \\ \text{Multiply the numerators and denominators.} &R(x)=\dfrac{2(x−3)(x−5)(x+5)}{2(x−3)(x−5)(x+5)} \\ & \\ \text{Remove common factors.} &R(x)=\dfrac{\cancel{2}\cancel{(x−3)}\cancel{(x−5)}\cancel{(x+5)}}{\cancel{2}\cancel{(x−3)}\cancel{(x−5)}\cancel{(x+5)}} \\ & \\ \text{Simplify.} &R(x)=1 \end{array}\)
找出\(R(x)=f(x)·g(x)\)位置\(f(x)=\dfrac{3x−21}{x^2−9x+14}\)和\(g(x)=\dfrac{2x^2−8}{3x+6}\).
- 回答
-
\(R(x)=2\)
找出\(R(x)=f(x)·g(x)\)位置\(f(x)=\dfrac{x^2−x}{3x^2+27x−30}\)和\(g(x)=\dfrac{x^2−100}{x^2−10x}\).
- 回答
-
\(R(x)=\dfrac{1}{3}\)
为了除以有理函数,我们使用与划分有理表达式相同的方法对方程右侧生成的有理表达式进行分割。
找出\(R(x)=\dfrac{f(x)}{g(x)}\)位置\(f(x)=\dfrac{3x^2}{x^2−4x}\)和\(g(x)=\dfrac{9x^2−45x}{x^2−7x+10}\).
解决方案
\(\begin{array} {ll} &R(x)=\dfrac{f(x)}{g(x)} \\ \text{Substitute in the functions }f(x),\space g(x). &R(x)=\dfrac{\dfrac{3x^2}{x^2−4x}}{\dfrac{9x^2−45x}{x^2−7x+10}} \\ & \\ \begin{array} {l} \text{Rewrite the division as the product of} \\ f(x)\text{ and the reciprocal of }g(x). \end{array} &R(x)=\dfrac{3x^2}{x^2−4x}·\dfrac{x^2−7x+10}{9x^2−45x} \\ & \\ \begin{array} {l} \text{Factor the numerators and denominators} \\ \text{and then multiply.} \end{array} &R(x)=\dfrac{3·x·x·(x−5)(x−2)}{x(x−4)·3·3·x·(x−5)} \\ & \\ \text{Simplify by dividing out common factors.} &R(x)=\dfrac{\cancel{3}·\cancel{x}·\cancel{x}\cancel{(x−5)}(x−2)}{\cancel{x}(x−4)·\cancel{3}·3·\cancel{x}\cancel{(x−5)}} \\ & \\ &R(x)=\dfrac{x−2}{3(x−4)} \end{array}\)
找出\(R(x)=\dfrac{f(x)}{g(x)}\)位置\(f(x)=\dfrac{2x^2}{x^2−8x}\)和\(g(x)=\dfrac{8x^2+24x}{x^2+x−6}\).
- 回答
-
\(R(x)=\dfrac{x−2}{4(x−8)}\)
找出\(R(x)=\dfrac{f(x)}{g(x)}\)位置\(f(x)=\dfrac{15x^2}{3x^2+33x}\)和\(g(x)=\dfrac{5x−5}{x^2+9x−22}\).
- 回答
-
\(R(x)=\dfrac{x(x−2)}{x−1}\)
关键概念
- 确定未定义有理表达式的值。
- 将分母设置为零。
- 求解方程。
- 等效分数属性
如果\(a\)\(b\)、和\(c\)是数字,其中\(b\neq 0\)、\(c\neq 0\)、then
\(\quad\dfrac{a}{b}=\dfrac{a·c}{b·c}\) 和\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\) - 如何简化理性表达。
- 将分子和分母完全分解。
- 通过划分常见因素进行简化。
- 理性表达中的对立
面恰恰相反\(b−a\)。\(a−b\)
\(\quad\dfrac{a−b}{b−a}=−1 \qquad a\neq b\)
表达式及其相反的除法为\(−1\)。 - 有理表达式的乘法
如果\(p\)、\(q\)\(r\)、和\(s\)是多项式 where\(q\neq 0\)、\(s\neq 0\)、then
\(\quad\dfrac{p}{q}·\dfrac{r}{s}=\dfrac{pr}{qs}\) - 如何乘以有理表达式。
- 将每个分子和分母完全分解。
- 将分子和分母相乘。
- 通过划分常见因素进行简化。
- 有理表达式的除法
如果\(p\)\(q\)\(r\)、、和\(s\)是多项式\(q\neq 0\),其中\(r\neq 0\),\(s\neq 0\),那么
\(\quad\dfrac{p}{q}÷\dfrac{r}{s}=\dfrac{p}{q}·\dfrac{s}{r}\) - 如何划分有理表达式。
- 将除法重写为第一个有理表达式的乘积和第二个有理表达式的倒数的乘积。
- 将分子和分母完全分解。
- 将分子和分母相乘。
- 通过划分常见因素进行简化。
- 如何确定有理函数的域。
- 将分母设置为零。
- 求解方程。
- 域是所有实数,不包括步骤 2 中找到的值。
词汇表
- 理性表达
- 有理表达式是形式的表达式\(\dfrac{p}{q}\),其中\(p\)和\(q\)是多项式和\(q\neq 0\)。
- 简化的有理表达
- 简化的有理表达式除了\(1\)分子和分母之外没有其他共同因素。
- 有理函数
- 有理函数是一种形式的函数,\(R(x)=\dfrac{p(x)}{q(x)}\)其中\(p(x)\)和\(q(x)\)是多项式函数\(q(x)\),不是零。


