6.2:按分组划分的最大公因子和因子
- Page ID
- 203929
在本节结束时,您将能够:
- 找出两个或多个表达式的最大公因子
- 分解多项式中的最大公因子
- 按分组分列
找出两个或多个表达式的最大公因子
之前我们将因子乘以得出产品。 现在,我们将扭转这个过程;我们将从产品开始,然后将其分解为其因素。 将产品拆分为因子称为因子分解。
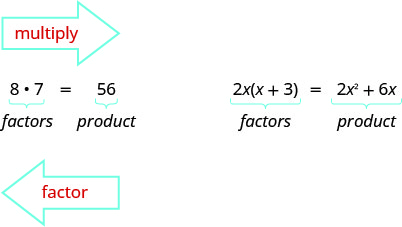
我们已经学会了如何对数字进行分解以找到两个或多个数字的最小公倍数(LCM)。 现在,我们将对表达式进行分解并找到两个或多个表达式的最大公因子。 我们使用的方法类似于我们用来查找 LCM 的方法。
两个或多个表达式的最大公因子 (GCF) 是作为所有表达式中因子的最大表达式。
我们总结了我们用来找到最大共同因素的步骤。
- 将每个系数分解为素数。 以扩展形式写入所有带有指数的变量。
- 列出所有因子-在一列中匹配常见因子。 在每列中,圈出常见因素。
- 记下所有表达式共有的共同因素。
- 将因子相乘。
下一个例子将向我们展示找到三个表达式的最大公因子的步骤。
找出最大的共同因素\(21x^3,\space 9x^2,\space 15x\).
- 回答
-
将每个系数分解为素数,然后以扩展形式写入带有指数的变量。 圈出每列中的常见因素。 记下常见的因素。 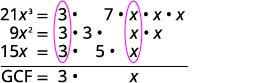
将因子相乘。 GCF\(=3x\) GCF 为\(21x^3\)\(9x^2\),\(15x\)是\(3x\)。
找出最大的共同因素:\(25m^4,\space 35m^3,\space 20m^2.\)
- 回答
-
\(5m^2\)
找到最大的共同因素:\(14x^3,\space 70x^2,\space 105x\).
- 回答
-
\(7x\)
从多项式中分解最大公因子
有时将数字表示为因子的乘积很有用,例如,12 as\(2·6\) or\(3·4\)。 在代数中,以因子形式表示多项式也很有用。 我们将从诸如此类的产品开始\(3x^2+15x\),最后是其因素\(3x(x+5)\)。 为此,我们 “反向” 应用分配财产。
我们在这里陈述分配财产,就像你在前面的章节中看到的那样,“相反”。
如果 a、b 和 c 是实数,那么
\[a(b+c)=ab+ac \quad \text{and} \quad ab+ac=a(b+c)\nonumber\]
左边的表格用于乘法。 右边的表单用于分数。
那么如何使用分布属性来分解多项式呢? 你只需找到所有项的 GCF,然后将多项式写成乘积即可!
因子:\(8m^3−12m^2n+20mn^2\)。
- 回答
-




因子:\(9xy^2+6x^2y^2+21y^3\)。
- 回答
-
\(3y^2(3x+2x^2+7y)\)
因子:\(3p^3−6p^2q+9pq^3\)。
- 回答
-
\(3p(p^2−2pq+3q^3)\)
- 找出多项式所有项的 GCF。
- 使用 GCF 将每个术语重写为产品。
- 使用 “反向” 分布属性对表达式进行分解。
- 通过乘以因子进行检查。
我们使用 “因子” 作为名词和动词:
\[\begin{array} {ll} \text{Noun:} &\hspace{50mm} 7 \text{ is a factor of }14 \\ \text{Verb:} &\hspace{50mm} \text{factor }3 \text{ from }3a+3\end{array}\nonumber\]
因子:\(5x^3−25x^2\)。
- 回答
-
找到\(5x^3\)和的 GCF\(25x^2\)。 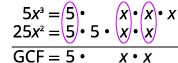
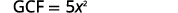
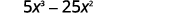
重写每个术语。 
将全球公积金考虑在内。 
查看:
\[5x^2(x−5) \nonumber\]\[5x^2·x−5x^2·5 \nonumber\]
\[5x^3−25x^2 \checkmark\nonumber\]
因子:\(2x^3+12x^2\)。
- 回答
-
\(2x^2(x+6)\)
因子:\(6y^3−15y^2\)。
- 回答
-
\(3y^2(2y−5)\)
因子:\(8x^3y−10x^2y^2+12xy^3\)。
- 回答
-
\(8x^3y,\space −10x^2y^2,\)和的 GCF\(12xy^3\)
是\(2xy\)。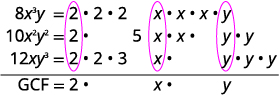

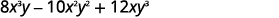
使用 GCF 重写每个术语\(2xy\)。 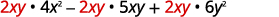
将全球公积金考虑在内。 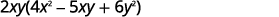
查看:
\[2xy(4x^2−5xy+6y^2)\nonumber\]\[2xy·4x^2−2xy·5xy+2xy·6y^2\nonumber\]
\[8x^3y−10x^2y^2+12xy^3\checkmark\nonumber\]
因子:\(15x^3y−3x^2y^2+6xy^3\)。
- 回答
-
\(3xy(5x^2−xy+2y^2)\)
因子:\(8a^3b+2a^2b^2−6ab^3\)。
- 回答
-
\(2ab(4a^2+ab−3b^2)\)
当前导系数为负时,我们将负值作为 GCF 的一部分除去。
因子:\(−4a^3+36a^2−8a\)。
- 回答
-
前导系数为负,因此 GCF 将为负。
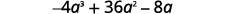
使用 GCF 重写每个术语\(−4a\)。 
将全球公积金考虑在内。 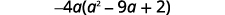
查看:
\[−4a(a^2−9a+2)\nonumber\]\[−4a·a^2−(−4a)·9a+(−4a)·2\nonumber\]
\[−4a^3+36a^2−8a\checkmark\nonumber\]
因子:\(−4b^3+16b^2−8b\)。
- 回答
-
\(−4b(b^2−4b+2)\)
因子:\(−7a^3+21a^2−14a\)。
- 回答
-
\(−7a(a^2−3a+2)\)
到目前为止,我们最大的共同因素是单项式。 在下一个示例中,最大的公因子是二项式。
因子:\(3y(y+7)−4(y+7)\)。
- 回答
-
GCF 是二项式\(y+7\)。
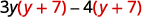
将全球公积金考虑在内,\((y+7)\)。 \((y+7)(3 y-4)\) 通过乘法自行检查。
因子:\(4m(m+3)−7(m+3)\)。
- 回答
-
\((m+3)(4m−7)\)
因子:\(8n(n−4)+5(n−4)\)。
- 回答
-
\((n−4)(8n+5)\)
按分组排序
有时候,多项式的所有项都没有共同因子。 当有四个项时,我们将多项式分成两部分,每部分有两个项。 然后在每个部分中查找 GCF。 如果多项式可以分解,你会发现两个部分都有一个共同的因子。 并非所有的多项式都可以分解。 就像有些数字是素数一样,有些多项式是素数。
按分组排序:\(xy+3y+2x+6\).
- 回答
-




按分组排序:\(xy+8y+3x+24\).
- 回答
-
\((x+8)(y+3)\)
按分组排序:\(ab+7b+8a+56\).
- 回答
-
\((a+7)(b+8)\)
- 对具有共同因素的术语进行分组。
- 排除每组中的共同因素。
- 从表达式中分解公共因子。
- 通过乘以因子进行检查。
按分组排序:ⓐ\(x^2+3x−2x−6\) ⓑ\(6x^2−3x−4x+2\)。
- 回答
-
ⓐ
\(\begin{array} {ll} \text{There is no GCF in all four terms.} &x^2+3x−2x−6 \\ \text{Separate into two parts.} &x^2+3x\quad −2x−6 \\ \begin{array} {l} \text{Factor the GCF from both parts. Be careful} \\ \text{with the signs when factoring the GCF from} \\ \text{the last two terms.} \end{array} &x(x+3)−2(x+3) \\ \text{Factor out the common factor.} &(x+3)(x−2) \\ \text{Check on your own by multiplying.} & \end{array}\)
ⓑ
\(\begin{array} {ll} \text{There is no GCF in all four terms.} &6x^2−3x−4x+2 \\ \text{Separate into two parts.} &6x^2−3x\quad −4x+2\\ \text{Factor the GCF from both parts.} &3x(2x−1)−2(2x−1) \\ \text{Factor out the common factor.} &(2x−1)(3x−2) \\ \text{Check on your own by multiplying.} & \end{array}\)
按分组排序:ⓐ\(x^2+2x−5x−10\) ⓑ\(20x^2−16x−15x+12\)。
- 回答
-
ⓐ\((x−5)(x+2)\)
ⓑ\((5x−4)(4x−3)\)
按分组排序:ⓐ\(y^2+4y−7y−28\) ⓑ\(42m^2−18m−35m+15\)。
- 回答
-
ⓐ\((y+4)(y−7)\)
ⓑ\((7m−3)(6m−5)\)
关键概念
- 如何找到两个表达式的最大公因子(GCF)。
- 将每个系数分解为素数。 以扩展形式写入所有带有指数的变量。
- 列出所有因子-在一列中匹配常见因子。 在每列中,圈出常见因素。
- 记下所有表达式共有的共同因素。
- 将因子相乘。
- 分布属性:如果\(a\)、\(b\)和\(c\)是实数,那么
\[a(b+c)=ab+ac\quad \text{and}\quad ab+ac=a(b+c)\nonumber\]
左边的表格用于乘法。 右边的表单用于分数。 - 如何分解多项式中的最大公因子。
- 找出多项式所有项的 GCF。
- 使用 GCF 将每个术语重写为产品。
- 使用 “反向” 分布属性对表达式进行分解。
- 通过乘以因子进行检查。
- 因子作为名词和动词:我们使用 “因子” 既是名词又是动词。
\[\begin{array} {ll} \text{Noun:} &\quad 7 \text{ is a factor of } 14\\ \text{Verb:} &\quad \text{factor }3 \text{ from }3a+3\end{array}\nonumber\]
- 如何按分组进行分解。
- 对具有共同因素的术语进行分组。
- 排除每组中的共同因素。
- 从表达式中分解公共因子。
- 通过乘以因子进行检查。
词汇表
- 保理
- 将产品拆分为因子称为因子分解。
- 最大的共同因素
- 两个或多个表达式的最大公因子 (GCF) 是作为所有表达式中因子的最大表达式。


