4.2: 求解具有两个变量的线性方程组
- Page ID
- 203900
在本节结束时,您将能够:
- 确定有序对是否是方程组的解
- 通过绘图求解线性方程组
- 通过替换求解方程组
- 通过消除求解方程组
- 选择最方便的方法来求解线性方程组
在开始之前,请参加这个准备测验。
确定有序对是否是方程组的解
在求解线性方程中,我们学习了如何用一个变量求解线性方程。 现在,我们将使用组合在一起的两个或多个线性方程,即所谓的线性方程组。
当两个或多个线性方程组合在一起时,它们形成线性方程组。
在本节中,我们将重点研究两个未知数中的两个线性方程组。 我们将在本章后面求解较大的方程组。
两个线性方程组的示例如下所示。 我们用大括号表示两个方程组合在一起形成方程组。
\[ \left\{ \begin{aligned} 2x+y & = 7 \\ x−2y & = 6 \end{aligned} \right. \nonumber \]
由两个变量(例如)组成的线性方程具有无限数量的解。\(2x+y=7\) 它的图形是一条线。 请记住,直线上的每个点都是方程的解,方程的每个解都是直线上的一个点。
为了求解一个由两个线性方程组成的系统,我们想找出作为两个方程解的变量的值。 换句话说,我们正在寻找使两个方程都成真的有序对\((x,y)\)。 这些被称为方程组的解。
方程组的解是使所有方程都成真的变量的值。 两个线性方程组的解由有序对表示\((x,y)\)。
为了确定有序对是否是两个方程组的解,我们将变量的值代入每个方程中。 如果有序对使两个方程都成立,则这是方程的解。
确定订购的配对是否是系统的解决方案\(\left \{ \begin{array} {l} x−y = −1 \\ 2x−y = −5 \end{array} \right. \)。
ⓐ\((−2,−1)\) ⓑ\((−4,−3)\)
- 回答
-
ⓐ
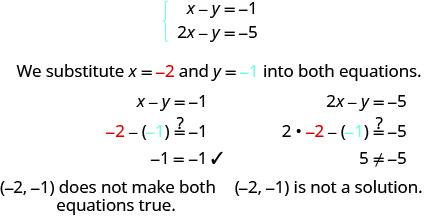
ⓑ
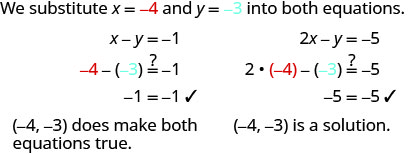
确定订购的配对是否是系统的解决方案\(\left \{ \begin{array} 3x+y = 0 \\ x+2y = −5 \end{array} \right. \)。
ⓐ\((1,−3)\) ⓑ\((0,0)\)
- 回答
-
ⓐ 是的 ⓑ 不
确定订购的配对是否是系统的解决方案\(\left \{ \begin{array} x−3y = −8 \\ −3x−y = 4 \end{array} \right. \)。
ⓐ\((2,−2)\) ⓑ\((−2,2)\)
- 回答
-
ⓐ 不 ⓑ 是的
通过绘图求解线性方程组
在本节中,我们将使用三种方法来求解线性方程组。 我们将使用的第一种方法是绘图。
线性方程的图形是一条直线。 直线上的每个点都是方程的解。 对于由两个方程组成的系统,我们将绘制两条直线。 然后我们可以看到作为每个方程解的所有点。 而且,通过找到这些线路的共同点,我们将找到系统的解决方案。
一个变量中的大多数线性方程都有一个解,但是我们看到一些称为矛盾的方程没有解,而对于其他称为恒等式的方程,所有数字都是解。
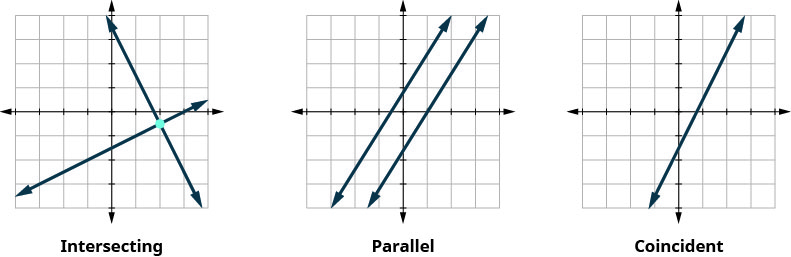
同样,当我们求解一个由两个线性方程组成的系统时,由同一平面中的两条线形表示的线性方程组时,有三种可能的情况,如图所示。
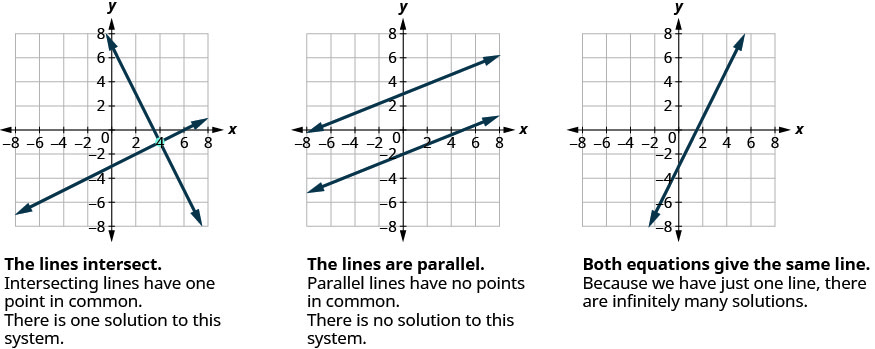
每次我们演示一种新方法时,我们都会在同一个线性方程组上使用它。 在本节的最后,你将决定哪种方法是解决这个系统的最便捷的方法。
通过绘制图表求解系统\( \left\{ \begin{array} {l} 2x+y = 7 \\ x−2y = 6 \end{array} \right. \)。
- 回答
-
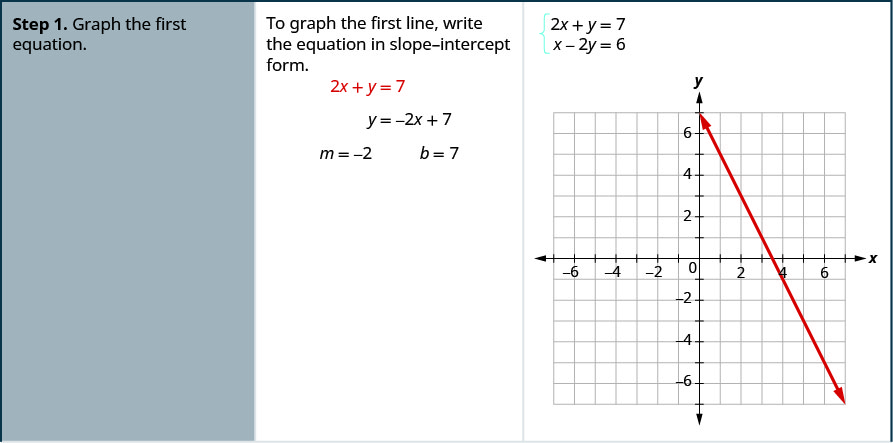
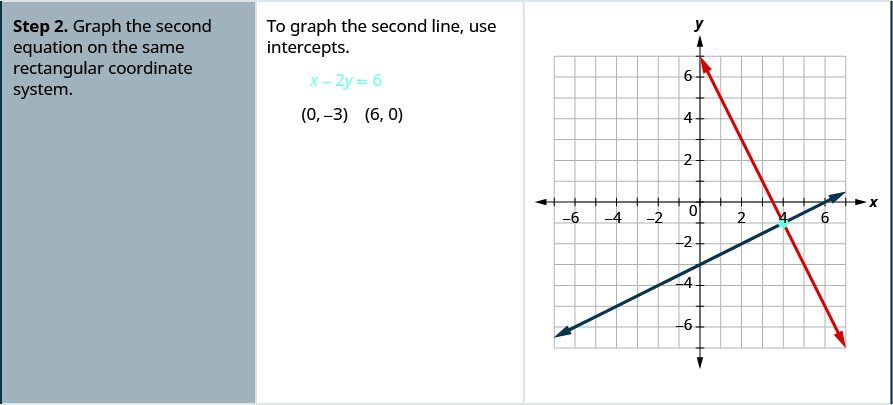


通过绘制图解系统:\( \left\{ \begin{array} {l} x−3y = −3 \\ x+y = 5 \end{array} \right. \).
- 回答
-
\((3,2)\)
通过绘制图表求解系统:\( \left\{ \begin{array} {l} −x+y = 1 \\ 3x+2y = 12 \end{array} \right.\)
- 回答
-
\((2,3)\)
此处显示了通过图表求解线性方程组的步骤。
- 绘制第一个方程的图形。
- 在同一个直角坐标系上绘制第二个方程的图形。
- 确定两条线是相交、平行还是同一条线。
- 确定系统的解决方案。
- 如果两条线相交,请确定交点。 这是系统的解决方案。
- 如果两条线是平行的,则系统没有解决方案。
- 如果两条线相同,则系统有无限数量的解。
- 检查两个方程中的解。
在下一个示例中,我们将首先将方程重写为斜率截距形式,因为这将使我们能够轻松地快速绘制线条图。
通过绘制图表求解系统:\(\left\{ \begin{array} {l} 3x+y = −1 \\ 2x+y = 0 \end{array}\right.\)
- 回答
-
我们将求解这两个方程,\(y\)这样我们就可以使用它们的斜率和\(y\)截距轻松绘制它们的图形。
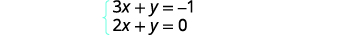
求解 y 的第一个方程。 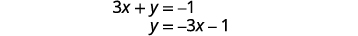
找出斜率和 y 截距。 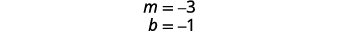
求解 y 的第二个方程。 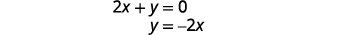
找出斜率和 y 截距。 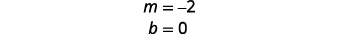
绘制线条图。 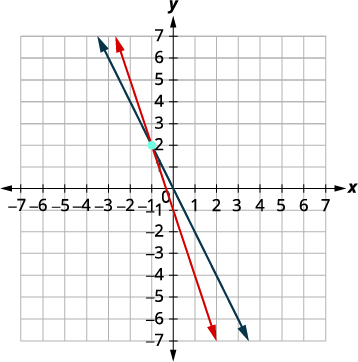
确定交叉点。 两条线相交于\((−1,2)\)。 检查两个方程中的解。
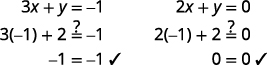
解决办法是\((−1,2)\)。
通过绘制图解系统:\(\left\{ \begin{array} {l} −x+y = 1 \\2x+y = 10 \end{array}\right. \).
- 回答
-
\((3,4)\)
通过绘制图解系统:\(\left\{ \begin{array} {l} 2x+y = 6 \\x+y = 1 \end{array}\right. \).
- 回答
-
\((5,−4)\)
到目前为止,在所有线性方程组中,直线相交,解为一个点。 在接下来的两个示例中,我们将看一个没有解的方程组和一个具有无限个解的方程组。
通过绘制图解系统:\(\left\{ \begin{array} {l} y = \tfrac{1}{2}x-3 \\ x-2y = 4 \end{array}\right. \).
- 回答
-
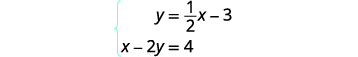
要绘制第一个方程,我们将使用其
斜率和 y 截距。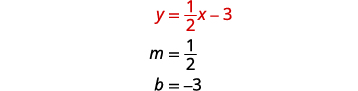
为了绘制第二个方程式,我们将使用
截距。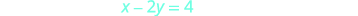
绘制线条图。 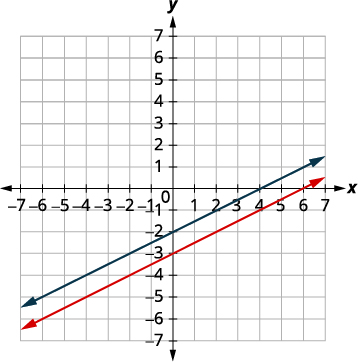
确定交叉点。 这些线是平行的。
由于两条线上都没有点,因此没有使两个方程都
成真的有
序对。 这个系统没有解决办法。
通过绘制图解系统:\(\left\{ \begin{array} {l} y = -\tfrac{1}{4}x+2 \\ x+4y = 4 \end{array}\right. \).
- 回答
-
没有解决办法
通过绘制图解系统:\(\left\{ \begin{array} {l} y = 3x-1 \\ 6x-2y = 6 \end{array}\right. \).
- 回答
-
没有解决办法
有时,系统中的方程表示同一条线。 由于直线上的每个点都使两个方程都成真,因此有无限多的有序对使两个方程都成真。 该系统有无限多的解决方案。
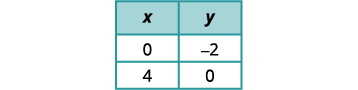
通过绘制图解系统:\(\left\{ \begin{array} {l} y = 2x-3 \\ -6x+3y = 9 \end{array}\right. \).
- 回答
-
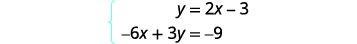
求出第一个方程的斜率和 y 截距。 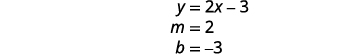
找出第二个方程的截距。 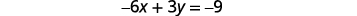
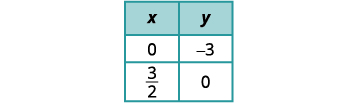
绘制线条图。 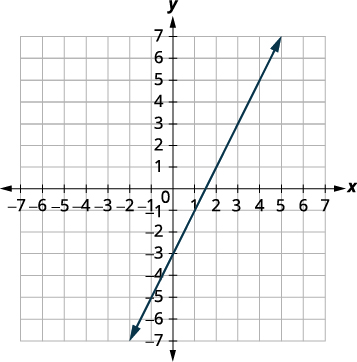
线条是一样的!
由于直线上的每个点都使两个
方程都成真,因此有无限多的有
序对使两个方程都成真。
这个系统有无限多的解决方案。如果你用斜率截距形式写第二个方程,你可能会意识到这些方程具有相同的斜率和相同的 y 截距。
通过绘制图解系统:\(\left\{ \begin{array} {l} y = -3x-6 \\ 6x+2y = -12 \end{array}\right. \).
- 回答
-
无限多的解决方案
通过绘制图解系统:\(\left\{ \begin{array} {l} y = \tfrac{1}{2}x-4 \\ 2x-4y = 16 \end{array}\right. \).
- 回答
-
无限多的解决方案
当我们在最后一个示例中绘制第二行时,我们将其绘制在第一行的正上方。 我们说这两条线是重合的。 重合线具有相同的斜率和相同的 y 截距。
重合线具有相同的斜率和相同的 y 截距。
示例和示例中的方程组各有两条相交线。 每个系统都有一个解决方案。
在示例中,方程给出了重合线,因此系统有无限多的解。
这三个示例中的系统至少有一个解决方案。 具有至少一个解的方程组称为一致方程组。
像示例这样的具有平行线的系统没有解决方案。 我们称之为这样的方程组不一致。 它没有解决办法。
一致的方程组是具有至少一个解的方程组。
不一致的方程组是没有解的方程组。
我们还通过称方程为独立方程或从属方程来对方程组中的方程进行分类。 如果两个方程是独立的,则每个方程都有自己的解集。 相交线和平行线是独立的。
如果两个方程是相关的,则一个方程的所有解也是另一个方程的解。 当我们绘制两个依赖方程时,我们会得到重合的线。
让我们通过查看三种类型的系统的图表来总结一下。 参见下文和表。
| 线条 | 相交 | 平行 | 重合 |
|---|---|---|---|
| 解决方案数量 | 1 点积分 | 没有解决办法 | 无限多 |
| 一致/不一致 | 一致 | 不一致 | 一致 |
| 受抚养人/独立 | 独立 | 独立 | 依赖的 |
在不绘制图表的情况下,确定解的数量,然后对方程组进行分类。
ⓐ\( \left\{ \begin{array} {l} y = 3x−1 \\ 6x−2y = 12 \end{array}\right. \) ⓑ\( \left\{ \begin{array} {l} 2x+y=−3 \\ x−5y=5 \end{array} \right. \)
- 回答
-
ⓐ 我们将比较这两条线的斜率和截距。
\(\begin{array} {lll} {} &{} &{ \left\{ \begin{array} {l} {y=3x-1} \\ {6x−2y=12} \end{array} \right. } \\ {} &{} &{y = 3x-1} \\ {\text{The first equation is already in slope-intercept form.}} &{} &{} \\ {\text{Write the second equation in slope-intercept form.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{6x-2y=12} \\ {} &{} &{-2y=-6x+12} \\ {} &{} &{\frac{-2y}{-2}=\frac{-6x+12}{-2}} \\ {} &{} &{y=3x-6} \\ {} &{y=3x-1} &{y=3x-6} \\ {} &{m=3} &{m=3} \\ {} &{b=-1} &{b=-6} \\ {\text{Find the slope and intercept of each line.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{\text{Since the slopes are the same andy-intercepts are}} &{} \\ {} &{\text{different, the lines are parallel.}} &{} \\ \end{array}\)
ⓑ 我们将比较这两条线的斜率和截距。
\(\begin{array} {lll} {} &{} &{} \\ {} &{ \left\{ \begin{array} {l} 2x+y=-3 \\ x-5y=5 \\ \end{array} \right. } &{} \\ {\text{Write both equations in slope–intercept form.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{2x+y=-3} &{x-5y=5} \\ {} &{y=-2x-3} &{-5y=-x+5} \\ {} &{} &{\frac{-5y}{-5}=\frac{-x+5}{-5}} \\ {} &{} &{y=\frac{1}{5}-1} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {\text{Find the slope and intercept of each line.}} &{} &{} \\ {} &{} &{} \\ {} &{y=-2x-3} &{y=\frac{1}{5}-1} \\ {} &{m=-2} &{m=\frac{1}{5}} \\ {} &{b=-3} &{b=-1} \\ {} &{} &{} \\ {} &{\text{Since the slopes are different, the lines intersect.}} &{} \\ \end{array}\)
图形相交的方程组有 1 个解,并且是一致且独立的。
在不绘制图表的情况下,确定解的数量,然后对方程组进行分类。
ⓐ\(\left\{ \begin{array} {l} y=−2x−4 \\ 4x+2y=9 \end{array} \right. \) ⓑ\(\left\{ \begin{array} {l} 3x+2y=2 \\ 2x+y=1 \end{array} \right. \)
- 回答
-
ⓐ 无解,不一致,独立 ⓑ 一个解决方案,一致,独立
在不绘制图表的情况下,确定解的数量,然后对方程组进行分类。
ⓐ\(\left\{ \begin{array} {l} y=\frac{1}{3}x−5 \\ x−3y=6 \end{array} \right. \) ⓑ\(\left\{ \begin{array} {l} x+4y=12 \\ −x+y=3 \end{array} \right. \)
- 回答
-
ⓐ 无解,不一致,独立 ⓑ 一个解决方案,一致,独立
通过绘图求解线性方程组是可视化可能产生的解类型的好方法。 但是,在许多情况下,通过绘图求解系统不方便或不精确。 如果图形延伸到小网格之外,x 和 y 都介于\(−10\)和 10 之间,则绘制线条可能很麻烦。 而且,如果系统的解不是整数,则可能很难从图表中精确读出它们的值。
通过替换求解方程组
现在,我们将使用替换法求解线性方程组。
我们将使用最初用于绘图的相同系统。
\[ \left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \nonumber \]
我们将首先求解 x 或 y 的其中一个方程。 我们可以选择任一方程并求解任一变量,但我们会尽量做出让工作变得容易的选择。
然后我们将该表达式替换为另一个方程。 结果是一个只有一个变量的方程——我们知道如何求解这些变量!
找到一个变量的值后,我们会将该值替换为一个原始方程并求解另一个变量。 最后,我们检查解并确保它使两个方程都成立。
通过替换求解系统:\( \left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \)
- 回答
-






通过替换求解系统:\( \left\{ \begin{array} {l} −2x+y=−11 \\ x+3y=9 \end{array} \right. \)
- 回答
-
\((6,1)\)
通过替换求解系统:\( \left\{ \begin{array} {l} 2x+y=−1 \\ 4x+3y=3 \end{array} \right. \)
- 回答
-
\((−3,5)\)
- 求解任一变量的其中一个方程。
- 将步骤 1 中的表达式替换为另一个方程。
- 求解由此产生的方程。
- 将步骤 3 中的解替换为任一原始方程以找到另一个变量。
- 将解写成有序对。
- 检查有序对是否是两个原始方程的解。
请务必小心下一个示例中的标志。
通过替换求解系统:\( \left\{ \begin{array} {l} 4x+2y=4 \\ 6x−y=8 \end{array} \right. \)
- 回答
-
我们需要为一个变量求解一个方程。 我们将求解 y 的第一个方程。
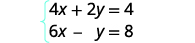
求解 y 的第一个方程。
在第二个方程中替换\(−2x+2\) y。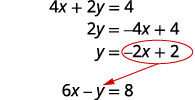
将 y 替换为\(−2x+2\)。 
求解 x 的方程。 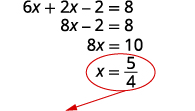
用替换\(x=54\)为\(4x+2y=4\)来找到 y。 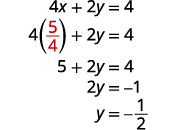
订购的对是\((54,−12)\)。 检查两个方程中的有序对。
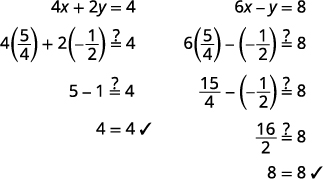
解决办法是\((54,−12)\)。
通过替换求解系统:\( \left\{ \begin{array} {l} x−4y=−4 \\ −3x+4y=0 \end{array} \right. \)
- 回答
-
\((2,32)\)
通过替换求解系统:\( \left\{ \begin{array} {l} 4x−y=0 \\ 2x−3y=5 \end{array} \right. \)
- 回答
-
\((−12,−2)\)
通过消除求解方程组
我们已经通过绘图和替换求解了线性方程组。 当变量系数很小且解具有整数值时,绘图效果很好。 当我们可以轻松地为其中一个变量求解一个方程并且生成的表达式中没有太多分数时,替换效果很好。
求解线性方程组的第三种方法称为消除法。 当我们通过替换求解一个系统时,我们从两个方程和两个变量开始,然后将其简化为一个带有一个变量的方程。 这也是我们要用淘汰法做的事情,但我们会有不同的方法来实现目标。
消除法基于 “相等” 的加法属性。 平等的加法属性说,当你将相同的量添加到方程的两边时,你仍然相等。 我们将扩展相等的加法属性,即当你向方程的两边添加相等的量时,结果是相等的。
对于任何表达式 a、b、c 和 d。
\[\begin{array} {ll} {\text{if}} &{a=b} \\ {\text{and}} &{c=d} \\ {\text{then}} &{a+c=b+d.} \\ \nonumber \end{array}\]
要通过消除求解方程组,我们从两个标准形式的方程开始。 然后我们决定哪个变量最容易消除。 我们如何决定? 我们希望一个变量的系数相对,这样我们就可以将方程加在一起并消除该变量。
注意当我们将这两个方程相加时它是如何工作的:
\[\left\{ \begin{array} {l} 3x+y=5 \\ \underline{2x−y=0} \end{array} \right. \nonumber\]
\[5x=5 \nonumber\]
y 相加为零,我们有一个方程和一个变量。
让我们再试一个:
\[ \left\{ \begin{array} x+4y=2 \\ 2x+5y=−2 \end{array} \right. \nonumber\]
这次我们看不到添加方程后可以立即消除的变量。
但是,如果我们将第一个方程乘以\(−2\),我们将得出 x 对立面的系数。 我们必须将方程两边的每个项乘以\(−2\)。
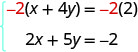
然后重写方程组。
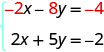
现在我们看到 x 项的系数是相反的,所以当我们将这两个方程相加时 x 将被消除。
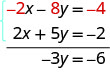
一旦我们得到一个只有一个变量的方程,我们就求解它。 然后我们将该值替换为原始方程之一,以求解剩余的变量。 而且,与往常一样,我们会检查答案以确保它是两个原始方程的解。
现在我们将看看如何使用消除来求解我们通过绘图和替换求解的相同方程组。
通过消除来解决系统:\(\left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \)
- 回答
-






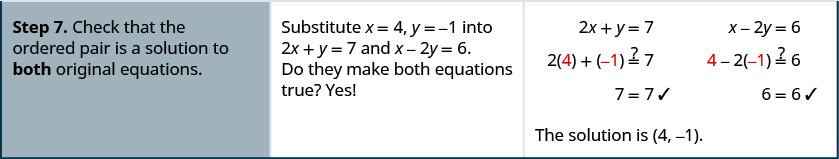
通过消除来解决系统:\(\left\{ \begin{array} {l} 3x+y=5 \\ 2x−3y=7 \end{array} \right.\)
- 回答
-
\((2,−1)\)
通过消除来解决系统:\(\left\{ \begin{array} {l} 4x+y=−5 \\ −2x−2y=−2 \end{array} \right.\)
- 回答
-
\((−2,3)\)
此处列出了这些步骤以便于参考。
- 用标准形式写下两个方程式。 如果有任何系数是分数,请将其清除。
- 使一个变量的系数成对立面。
- 决定要消除哪个变量。
- 将一个或两个方程相乘,使该变量的系数相反。
- 将步骤 2 得出的方程相加,以消除一个变量。
- 求解剩余变量。
- 将步骤 4 中的解替换为原始方程之一。 然后求解另一个变量。
- 将解写成有序对。
- 检查有序对是否是两个原始方程的解。
现在我们举一个例子,我们需要将两个方程乘以常量,以便使一个变量的系数对立。
通过消除来解决系统:\(\left\{ \begin{array} {l} 4x−3y=9 \\ 7x+2y=−6 \end{array} \right. \)
- 回答
-
在这个例子中,我们不能仅将一个方程乘以任何常量来获得相反的系数。 因此,我们将策略性地将两个方程乘以不同的常量得出对立面。
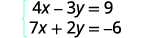
两个方程都是标准形式。
为了得到 y 的相反系数,我们将第一个方程
乘以 2,将
第二个方程乘以 3。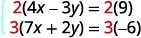
简化。 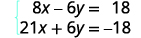
将两个方程相加以消除 y。 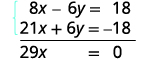
求解 x。 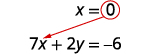
将 x=0x=0 替换为原始方程之一。 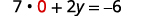
求解 y。 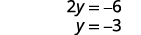
将解写成有序对。 订购的对是\((0,−3)\)。
检查有序对是否是
两个原始方程的解。
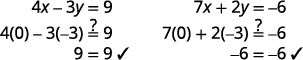
解决办法是\((0,−3)\)。
通过消除来解决系统:\(\left\{ \begin{array} {l} 3x−4y=−9 \\ 5x+3y=14\end{array} \right. \)
- 回答
-
\((1,3)\)
通过消除来求解每个系统:\(\left\{ \begin{array} {l} 7x+8y=4 \\ 3x−5y=27 \end{array} \right.\)
- 回答
-
\((4,−3)\)
当方程组包含分数时,我们将首先通过将每个方程乘以方程中所有分数的 LCD 来清除分数。
通过消除来解决系统:\(\left\{ \begin{array} {l} x+\tfrac{1}{2}y=6 \\ \tfrac{3}{2}x+\tfrac{2}{3}y=\tfrac{17}{2} \end{array} \right.\)
- 回答
-
在此示例中,两个方程都有分数。 我们的第一步是将每个方程乘以方程中所有分数的液晶显示器,以清除分数。
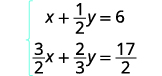
要清除分数,请将每个
方程乘以其 LCD。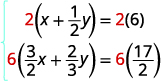
简化。 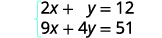
现在我们已经准备好消除
其中一个变量了。 请注意,两个方程都是
标准形式。我们可以通过将顶部方程乘以来消除 y\(−4\)。 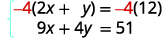
简化并添加。
替换\(x=3\)成原始方程之一。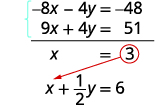
求解 y。 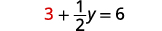
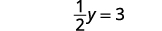
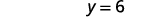
将解写成有序对。 订购的对是\((3,6)\)。 检查有序对是否是
两个原始方程的解。

解决方案是\((3,6)\)。
通过消除来求解每个系统:\(\left\{ \begin{array} {l} \tfrac{1}{3}x−\tfrac{1}{2}y=1 \\ \tfrac{3}{4}x−y=\tfrac{5}{2} \end{array} \right.\)
- 回答
-
\((6,2)\)
通过消除来求解每个系统:\(\left\{ \begin{array} {l} x+\tfrac{3}{5}y=−\tfrac{1}{5} \\ −\tfrac{1}{2}x−\tfrac{2}{3}y=\tfrac{5}{6} \end{array} \right.\)
- 回答
-
\((1,−2)\)
当我们通过图表求解方程组时,我们发现并非所有的线性方程组都有单个有序对作为解。 当两个方程实际上是同一条线时,有无限多的解。 我们称之为一致的系统。 当两个方程描述平行线时,没有解。 我们称之为不一致的系统。
使用替换或淘汰也是如此。 如果置换或消除末尾的方程是真实的陈述,那么我们有一个一致但依赖的系统,方程组有无限多的解。 如果置换或消除末尾的方程是错误的陈述,则我们的方程组不一致,方程组没有解。
通过消除来解决系统:\(\left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\tfrac{3}{4}x \end{array} \right. \)
- 回答
-
\(\begin{array} {ll} {} &{ \left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\frac{3}{4}x \end{array} \right.} \\ {} &{} \\ {\text{Write the second equation in standard form.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ \frac{3}{4}x+y=3 \end{array} \right. } \\ {} &{} \\ {\text{Clear the fractions by multiplying the } \\ \text{second equation by 4.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ 4(\frac{3}{4}x+y)=4(3) \end{array} \right. } \\ {} &{} \\ {\text{Simplify.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ 3x+4y=12 \end{array} \right. } \\ {} &{} \\ {\text{To eliminate a variable, we multiply the} \\ \text{second equation by−1. Simplify and add.}} &{\begin{array} {l} {\left\{ \begin{array} {l} 3x+4y=12 \\ \underline{-3x-4y=-12 } \end{array} \right.} \\ {\hspace{16mm} 0=0} \end{array}} \\ \end{array} \)
这是真实的陈述。 这些方程是一致的,但相互依存。 他们的图形将是同一条线。 该系统有无限多的解决方案。
在我们清除了第二个方程中的分数之后,你有没有注意到这两个方程是相同的? 这意味着我们有重合的线。
通过消除来解决系统:\(\left\{ \begin{array} {l} 5x−3y=15 \\ 5y=−5+\tfrac{5}{3}x \end{array} \right. \)
- 回答
-
无限多的解决方案
通过消除来解决系统:\(\left\{ \begin{array} {l} x+2y=6 \\ y=−\tfrac{1}{2}x+3\end{array} \right. \)
- 回答
-
无限多的解决方案
选择最方便的方法来求解线性方程组
当您在应用程序中求解线性方程组时,不会被告知要使用哪种方法。 你需要自己做这个决定。 因此,您需要选择最容易做到、最大限度地减少出错机会的方法。
\[ \textbf{Choose the Most Convenient Method to Solve a System of Linear Equations} \\ \begin{array} {lll} {\underline{\textbf{Graphing}}} &{\underline{\textbf{Substitution}}} &{\underline{\textbf{Elimination}}} \\ {\text{Use when you need a}} &{\text{Use when one equation is}} &{\text{Use when the equations a}} \\ {\text{picture of the situation.}} &{\text{already solved or can be}} &{\text{rein standard form.}} \\ {\text{}} &{\text{easily solved for one}} &{\text{}} \\ {\text{}} &{\text{variable.}} &{\text{}} \\ \end{array} \nonumber \]
对于每个线性方程组,决定通过替换还是消除来求解更方便。 解释你的答案。
ⓐ\(\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=−32 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} 5x+6y=12 \\ y=\tfrac{2}{3}x−1 \end{array} \right.\)
- 回答
-
ⓐ
\[\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=−32 \end{array} \right.\nonumber\]
由于两个方程都是标准形式,因此使用消除将最为方便。
ⓑ
\[\left\{ \begin{array} {l} 5x+6y=12 \\ y=\tfrac{2}{3}x−1 \end{array} \right.\nonumber \]
由于 y 已经求解了一个方程,因此使用替换将最为方便。
对于每个线性方程组,决定通过替换还是消除来求解更方便。 解释你的答案。
ⓐ\(\left\{ \begin{array} {l} 4x−5y=−32 \\ 3x+2y=−1 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} x=2y−1 \\ 3x−5y=−7 \end{array} \right.\)
- 回答
-
ⓐ 由于两个方程都是标准形式,因此使用消除将最为方便。ⓑ 由于一个方程已经求解了 x,因此使用替换最为方便。
对于每个线性方程组,决定通过替换还是消除来求解更方便。 解释你的答案。
ⓐ\(\left\{ \begin{array} {l} y=2x−1 \\ 3x−4y=−6 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} 6x−2y=12 \\ 3x+7y=−13 \end{array} \right.\)
- 回答
-
ⓐ 由于 y 已经求解了一个方程,因此使用替换将最为方便。ⓑ 由于两个方程都是标准形式,因此使用消除最为方便。
关键概念
- 如何通过绘图求解线性方程组。
- 绘制第一个方程的图形。
- 在同一个直角坐标系上绘制第二个方程的图形。
- 确定两条线是相交、平行还是同一条线。
- 确定系统的解决方案。
如果两条线相交,请确定交点。 这是系统的解决方案。
如果两条线是平行的,则系统没有解决方案。
如果两条线相同,则系统有无限数量的解。 - 检查两个方程中的解。
- 如何通过替换求解方程组。
- 求解任一变量的其中一个方程。
- 将步骤 1 中的表达式替换为另一个方程。
- 求解由此产生的方程。
- 将步骤 3 中的解替换为任一原始方程以找到另一个变量。
- 将解写成有序对。
- 检查有序对是否是两个原始方程的解。
- 如何通过消除求解方程组。
- 用标准形式写下两个方程式。 如果有任何系数是分数,请将其清除。
- 使一个变量的系数成对立面。
决定要消除哪个变量。
将一个或两个方程相乘,使该变量的系数相反。 - 将步骤 2 得出的方程相加,以消除一个变量。
- 求解剩余变量。
- 将步骤 4 中的解替换为原始方程之一。 然后求解另一个变量。
- 将解写成有序对。
- 检查有序对是否是两个原始方程的解。 \[ \textbf{Choose the Most Convenient Method to Solve a System of Linear Equations} \\ \begin{array} {lll} {\underline{\textbf{Graphing}}} &{\underline{\textbf{Substitution}}} &{\underline{\textbf{Elimination}}} \\ {\text{}} &{\text{Use when one equation is}} &{\text{}} \\ {\text{Use when you need a}} &{\text{already solved or can be}} &{\text{Use when the equations a}} \\ {\text{picture of the situation.}} &{\text{easily solved for one}} &{\text{rein standard form.}} \\ {\text{}} &{\text{variable.}} &{\text{}} \\ \end{array} \nonumber \]
词汇表
- 重合线
- 重合线具有相同的斜率和相同的 y 截距。
- 一致和不一致的系统
- 一致方程组是指具有至少一个解的方程组;不一致方程组是没有解的方程组。
- 方程组的解
- 方程组的解是使所有方程成真的变量的值;解由有序对 (x, y) 表示。 (x, y)。
- 线性方程组
- 当两个或多个线性方程组合在一起时,它们形成线性方程组。