3.2:用两个变量绘制线性方程
- Page ID
- 203869
在本节结束时,您将能够:
- 在矩形坐标系中绘制点
- 通过绘制点来绘制线性方程图
- 绘制垂直线和水平线
- 找到\(x\)-和\(y\)-截取
- 使用截图绘制一条线
在矩形坐标系上绘制点
就像地图使用网格系统来识别位置一样,代数中使用网格系统来显示矩形坐标系中两个变量之间的关系。 矩形坐标系也称为\(xy\)-plane 或 “坐标平面”。
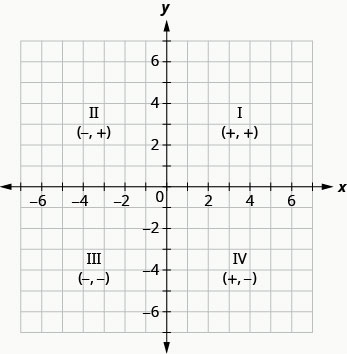
矩形坐标系由两条相交的数字线组成,一条是水平的,一条是垂直的。 水平数字线称为\(x\)-axis。 垂直数字线被称为\(y\)-axis。 这些轴将一个平面分成四个区域,称为象限。 象限由罗马数字标识,从右上角开始,逆时针移动。 见图\(\PageIndex{1}\)。
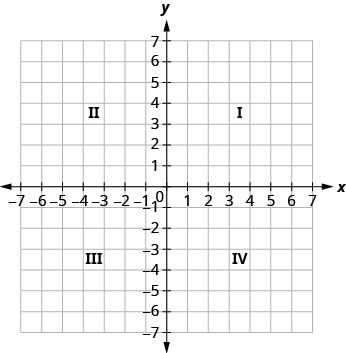
在矩形坐标系中,每个点都由一对有序表示。 有序对中的第一个数字是点\(x\)的坐标,第二个数字是点\(y\)的坐标。 短语 “有序配对” 表示顺序很重要。
有序对\((x,y)\)给出矩形坐标系中一个点的坐标。 第一个数字是\(x\)-坐标。 第二个数字是\(y\)-坐标。
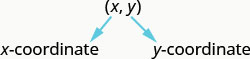
轴交叉点的有序对是什么? 此时两个坐标均为零,因此其有序对为\((0,0)\)。该点\((0,0)\)有一个特殊的名称。 它被称为起源。
该点\((0,0)\)被称为原点。 这是\(x\)-axis 和\(y\)-axis 相交的点。
我们使用坐标在\(xy\)-plane 上定位一个点。 让我们把这个点画\((1,3)\)成一个例子。 首先,在\(x\)-axis 上找到 1,然后轻描绘一条穿过的垂直线\(x=1\)。 然后,在\(y\)-axis\(3\) 上定位并绘制一条横线 No\(y=3.\) w,找到这两条线交汇的点,即带有坐标的点\((1,3)\)。 见图\(\PageIndex{2}\)。
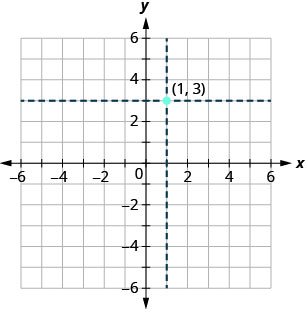
请注意,垂直线穿过\(x=1\)和水平线\(y=3\)不在图表中。 我们只是用它们来帮助我们找到重点\((1,3)\)。
当其中一个坐标为零时,该点位于其中一个轴上。 在图\(\PageIndex{3},\)中\((0,4)\),点在\(y\)-轴上,点\((−2,0)\)在\(x\)-轴上。
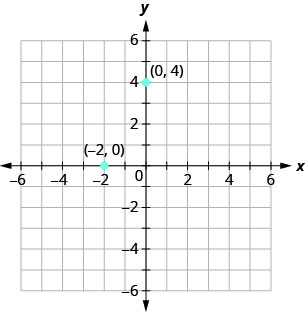
- \(y\)-坐标等于的点\(0\)位于\(x\)-axis 上,并且有坐标\((a,0)\)。
- \(x\)-坐标等于\(0\)的点位于\(y\)-axis 上,并且有坐标\((0,b)\)。
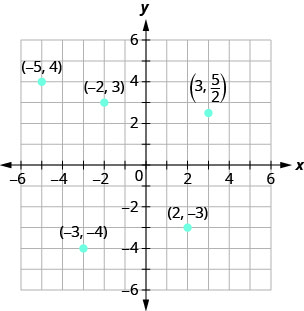
在矩形坐标系中绘制每个点并确定该点所在的象限:
a.\((−5,4\)) b.\((−3,−4)\) c.\((2,−3)\) d.\((0,−1)\) e\((3,\dfrac{5}{2})\).
解决方案
坐标对的第一个数字是\(x\)-坐标,第二个数字是\(y\)-坐标。 要绘制每个点,请绘制一条穿过\(x\)-坐标的垂直线和一条穿过\(y\)-坐标的水平线。 他们的交叉点才是重点。
- 因为\(x=−5\),该点在\(y\)-axis 的左边。 另外\(y=4\),因为该点在\(x\)-轴上方。 重点在\((−5,4)\)象限 II 中。
- 因为\(x=−3\),该点在\(y\)-axis 的左边。 另外\(y=−4\),因为该点在\(x\)-轴下方。 重点在\((−3,−4)\)象限 III 中。
- 因为\(x=2\),该点在\(y\)-轴的右边。 因为\(y=−3\),该点在\(x\)-轴下方。 重点在\((2,−3)\)象限 IV 中。
- 因为\(x=0\),坐标\((0,−1)\)为的点位于\(y\)-轴上。
- 因为\(x=3\),该点在\(y\)-轴的右边。 因为\(y=\dfrac{5}{2})\),该点在\(x\)-轴上方。 (写\(\dfrac{5}{2})\)成混合数字或十进制可能会有所帮助。) 重点在\((3,\dfrac{5}{2})\)象限 I 中
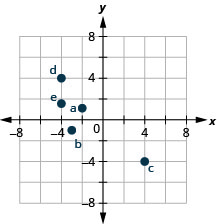
在矩形坐标系中绘制每个点并确定该点所在的象限:
a.\((−2,1)\) b.\((−3,−1)\) c.\((4,−4)\) d.\((−4,4)\) e.\((−4,\dfrac{3}{2})\)
- 回答
-
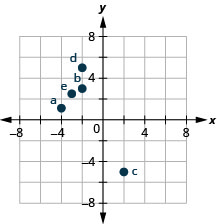
在矩形坐标系中绘制每个点并确定该点所在的象限:
a.\((−4,1)\) b.\((−2,3)\) c.\((2,−5)\) d.\((−2,5)\) e.\((−3,\dfrac{5}{2})\)
- 回答
-
\(x\)-坐标和\(y\)-坐标的符号会影响点的位置。 在上一个示例中绘制点图时,您可能已经注意到了一些模式。 我们可以用这种方式总结象限的符号模式:
| 象限 I | 象限二 | 象限三 | 象限四 |
| \((x,y)\) | \((x,y)\) | \((x,y)\) | \((x,y)\) |
| \((+,+)\) | \((−,+)\) | \((−,−)\) | \((+,−)\) |
到目前为止,你求解的所有方程都是只有一个变量的方程。 在几乎所有情况下,当你求解方程时,你只得到了一个解。 但是方程可以有多个变量。 具有两个变量的方程可以采用以下形式\(Ax+By=C\)。 这种形式的方程称为由两个变量组成的线性方程。
形式为的方程\(Ax+By=C\),其中\(A\)和\(B\)均不为零,称为由两个变量组成的线性方程。
以下是两个变量中的线性方程的示例,\(x\)和\(y\)。
\ (\ begin {align*} {\ color {brickRed} A} x + {\ color {RoyalBlue} B} y &= {\ color {forestgreen} C}\\\ [5pt]
x+ {\ color {royalBlue} 8}\ end {align*}\)
\({\color{BrickRed}A = 1}\),\({\color{RoyalBlue}B = 4}\),\({\color{forestgreen}C=8}\)
该方程也\(y=−3x+5\)是一个线性方程。 但它似乎不是这种形式\(Ax+By=C\)。 我们可以使用 Equality 的加法属性并将其重写为\(Ax+By=C\)表单。
\[ \begin{array} {lrll} {} &{y} &= &{-3x+5} \\ {\text{Add to both sides.} } &{y+3x} &= &{3x+5+3x} \\ {\text{Simplify.} } &{y+3x} &= &{5} \\ {\text{Use the Commutative Property to put it in} } &{} &{} &{} \\ {Ax+By=C\text{ form.} } &{3x+y} &= &{5} \end{array} \nonumber\]
通过重写\(y=−3x+5\)为\(3x+y=5\),我们可以很容易地看出它是两个变量的线性方程,因为它的形式是\(Ax+By=C\)。 当方程采用这种形式时\(Ax+By=C\),我们说它是线性方程的标准形式。
线性方程在书写时采用标准形式\(Ax+By=C\)。
大多数人更喜欢拥有\(A,\)\(B,\)和\(C\)成为整数,在以标准形式书写线性方程\(A \geq 0\)时,尽管这并不是绝对必要的。
线性方程有无限多的解。 对于每个替换的数字,都\(x\)有一个对应的\(y\)-value。 这对值是线性方程的解,由有序对表示\((x,y)\)。 当我们将\(x\)和的这些值替换\(y\)到方程中时,结果是真实的陈述,因为左侧的值等于右侧的值。
有序对\((x,y)\)是线性方程的解\(Ax+By=C\),前提是当有序对的\(x\)-和\(y\)-值被替换为方程时,方程为真陈述。
线性方程有无限多的解。 我们可以在直角坐标系中绘制这些解。 这些点将完美地排成一条直线。 我们将这些点用一条直线连接起来,得到方程图。 我们在直线的两端放置箭头,以表示该线向两个方向延伸。
图形是方程所有解的直观表示。 这是一句谚语的例子:“一张图片胜过千言万语。” 这条线显示了该方程的所有解。 直线上的每个点都是方程的解。 而且,这个方程的所有解都在这条线上。 这条线被称为方程图。 没上线的积分不是解决办法!
线性方程的图形\(Ax+By=C\)是一条直线。
- 直线上的每个点都是方程的解。
- 这个方程的每个解都是这条线上的一个点。
显示的\(y=2x−3\)图表。
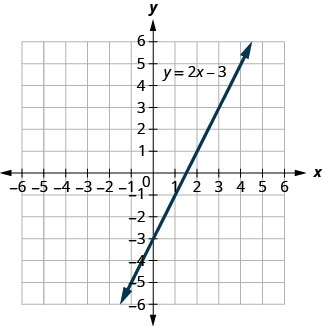
对于每对订购的配对,请决定:
- 有序对是方程的解吗?
- 点在直线上吗?
A:\((0,−3)\) B:\((3,3)\) C:\((2,−3)\) D:\((−1,−5)\)
解决方案:
将\(x\)-和\(y\)-值替换到方程中,以检查有序对是否是方程的解。
一个。
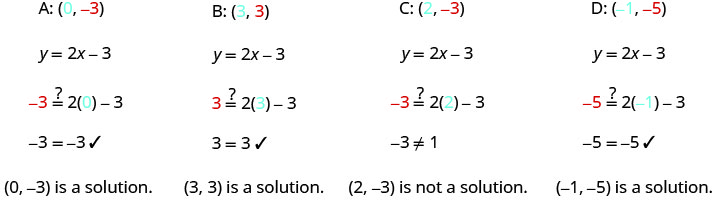
b. 绘制点\((0,−3)\)\((3,3)\)、\((2,−3)\)、和\((−1,−5)\)。
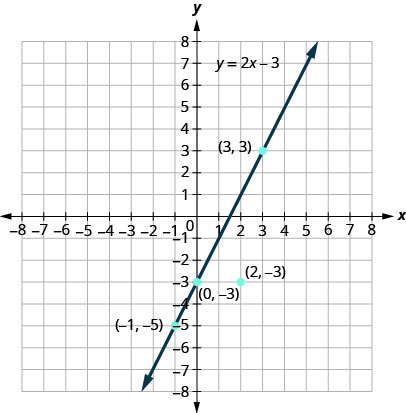
点\((0,3)\)\((3,−3)\)、\((−1,−5)\)和在线上\(y=2x−3\),点\((2,−3)\)不在线上。
作为解的\(y=2x−3\)点在线上,但不是解的点不在线上。
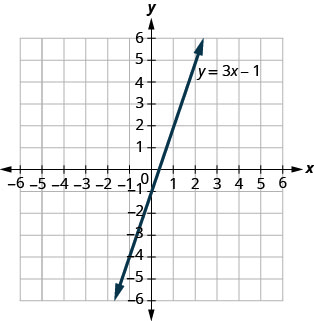
使用图表\(y=3x−1\)。 对于每对订购的配对,请决定:
a. 有序对是方程的解吗?
b. 点在直线上吗?
A\((0,−1)\) B\((2,5)\)
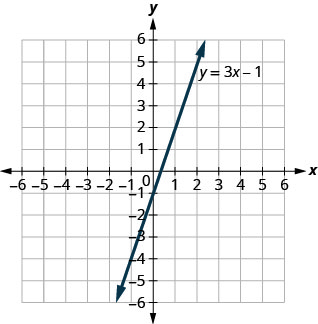
- 回答
-
a. 是的 b. 是的
使用图表\(y=3x−1\)。 对于每对订购的配对,请决定:
a. 有序对是方程的解吗?
b. 点在直线上吗?
A\((3,−1)\) B\((−1,−4)\)
- 回答
-
a. 不 b. 是的
通过绘制点来绘制线性方程图
有几种方法可用于绘制线性方程。 我们将使用的第一种方法称为绘制点图或点绘法。 我们找到三个坐标是方程解的点,然后在矩形坐标系中绘制它们。 通过将这些点连接成一条线,我们就有了线性方程的图形。
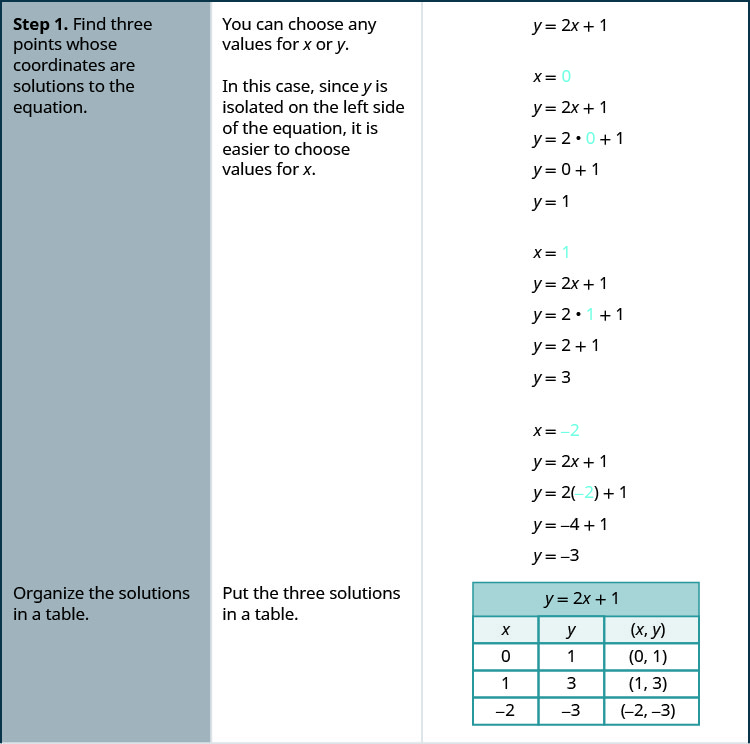
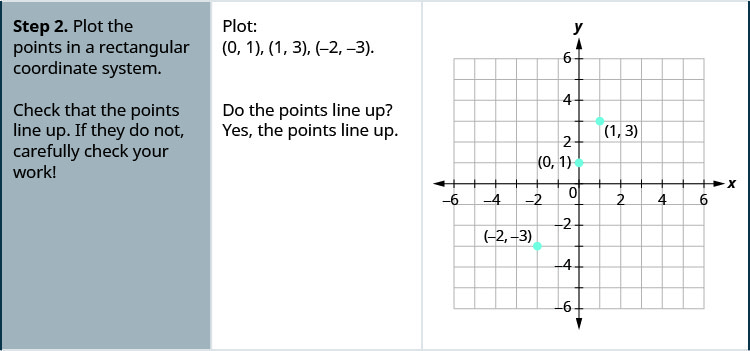
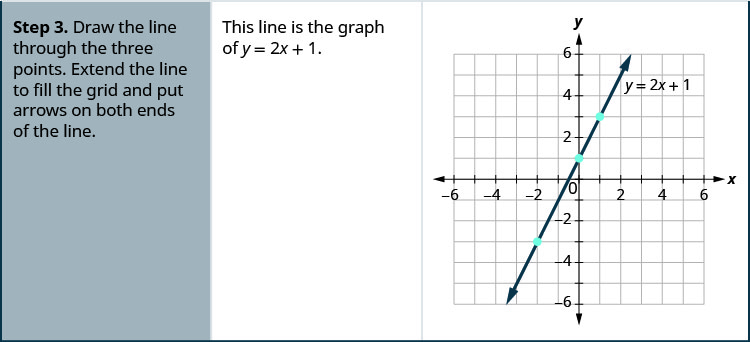
\(y=2x+1\)通过绘制点来绘制方程图。
解决方案:
通过绘制点来绘制方程图:\(y=2x−3\).
- 回答
-
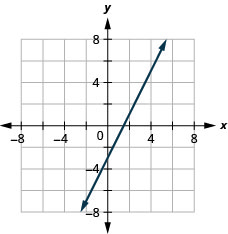
通过绘制点来绘制方程图:\(y=−2x+4\).
- 回答
-
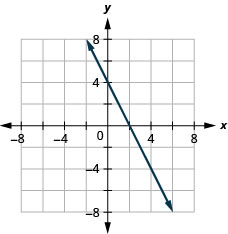
此处总结了通过绘制点绘制线性方程时要采取的步骤。
- 找出坐标为方程解的三个点。 将它们整理在桌子里。
- 在矩形坐标系中绘制点。 检查各点是否对齐。 如果没有,请仔细检查你的工作。
- 画一条穿过这三个点的直线。 延伸线条以填充网格,并在直线的两端放置箭头。
的确,确定一条线只需要两个点,但是使用三个点是个好习惯。 如果你只绘制两个点而其中一个点不正确,你仍然可以画一条线,但它不能代表方程的解。 这将是错误的路线。
如果您使用三个积分,而一个点不正确,则这些点将不会排成一列。 这告诉你出了点问题,你需要检查一下你的工作。 看看这些插图之间的区别。

当方程包含分数作为系数时,\(x,\)我们仍然可以用任何数字代替。\(x.\)但是,如果我们为 “好” 的值做出 “好” 的选择,算术会更容易。\(x.\)这样我们就可以避免分数答案,因为分数答案很难精确绘制。
绘制方程图:\(y=\frac{1}{2}x+3\).
解决方案:
找出作为方程解的三个点。 由于该方程的系数\(\dfrac{1}{2}\)为分数,因此\(x,\)我们将\(x\)谨慎选择的值。 我们将使用零作为一个选项,使用倍\(2\)数作为其他选项。 为什么二的倍数是值的好选择\(x\)? 通过选择乘法的倍数,\(\dfrac{1}{2}\)可以简化为整数\(2\)
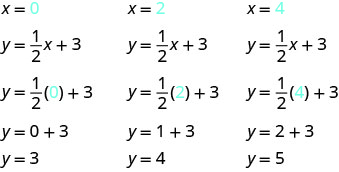
积分如表所示。
| \(y=\frac{1}{2}x+3\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| 0 | 3 | \((0,3)\) |
| 2 | 4 | \((2,4)\) |
| 4 | 5 | \((4,5)\) |
绘制点图,检查它们是否对齐,然后画出直线。
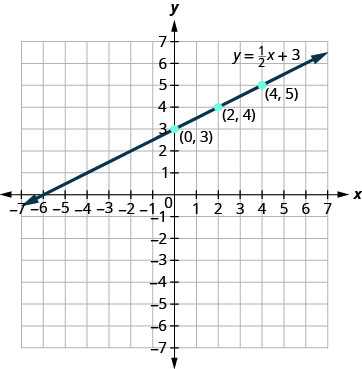
绘制方程图:\(y=\frac{1}{3}x−1\).
- 回答
-
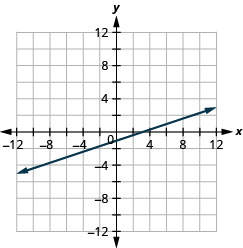
绘制方程图:\(y=\frac{1}{4}x+2\).
- 回答
-
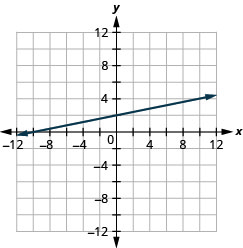
绘制垂直线和水平线
一些线性方程只有一个变量。 他们可能只有\(x\),没有,\(y,\)或者只是\(y\)没有。\(x.\)这改变了我们制作值表以绘制点数的方式。
让我们考虑一下这个方程式\(x=−3\)。 这个方程只有一个变量,\(x.\)方程表示\(x\)它总是等于\(−3\),所以它的值\(y.\)不依赖于不管值\(y,\)的值\(x\)是多少\(−3\)。
因此,要创建一个值表,请为所有\(x\)-\(−3\) values写入内容。 然后选择 Sinc\(y.\) e\(x\) 不依赖的任意值\(y,\)你可以选择任何你喜欢的数字。 但是为了拟合坐标图上的点,我们将使用 1、2 和 3 作为\(y\)坐标。 见表。
| \(x=−3\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| \(−3\) | 1 | \((−3,1)\) |
| \(−3\) | 2 | \((−3,2)\) |
| \((−3,)\) | 3 | \((−3,3)\) |
绘制表中的点并用直线将它们连接起来。 请注意,我们已经绘制了一条垂直线。
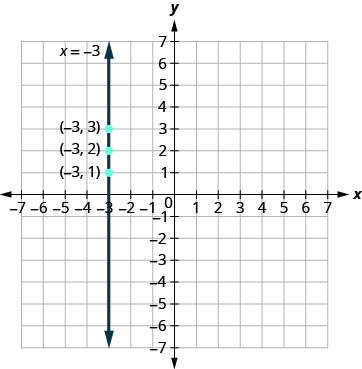
如果方程有\(y\)但没有\(x\)呢? 让我们绘制方程图\(y=4\)。 这次 y 值是一个常数,所以在这个方程中,表中的所有值都\(y\)不依赖\(4\)于 F\(x.\) ill in,然后选择任何值。\(x.\)我们将使用 0、2 和 4 作为\(x\)坐标。\(y\)
| \(y=4\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| 0 | 4 | \((0,4)\) |
| 2 | 4 | \((2,4)\) |
| 4 | 4 | \((4,4)\) |
在这张图中,我们绘制了一条穿过\(y\)-axis 的水平线\(4.\)
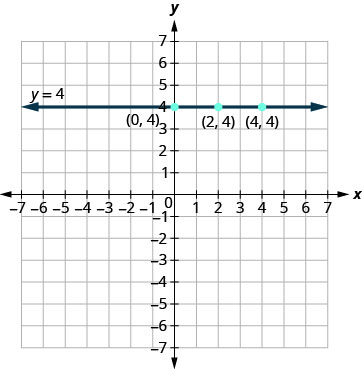
垂直线是这种形式的方程的图形\(x=a\)。
该直线穿过\(x\)-axis(位于处)\((a,0)\)。
水平线是这种形式的方程的图形\(y=b\)。
该直线穿过\(y\)-axis(位于处)\((0,b)\)。
图:a.\(x=2\) b\(y=−1\).
解决方案
a. 方程只有一个变量,\(x,\)并且\(x\)始终等于\(2.\)我们创建一个表,其中 always\(x\) 为 always\(2\) 然后输入任何值。图形是一条穿过\(x\)-axis 的垂直线\(y.\)\(2.\)
| \(x\) | \(y\) | \((x,y)\) |
|---|---|---|
| \ (x\)” data-valign= “middle” >2 | \ (y\)” data-valign= “middle” >1 | \ ((x, y)\)” data-valign= “middle” >\((2,1)\) |
| \ (x\)” data-valign= “middle” >2 | \ (y\)” data-valign= “middle” >2 | \ ((x, y)\)” data-valign= “middle” >\((2,2)\) |
| \ (x\)” data-valign= “middle” >2 | \ (y\)” data-valign= “middle” >3 | \ ((x, y)\)” data-valign= “middle” >\((2,3)\) |
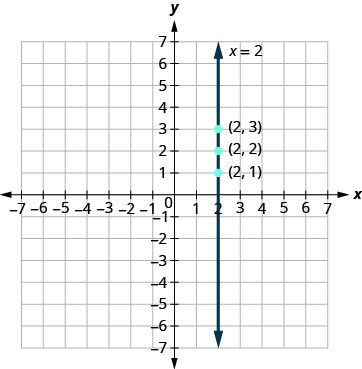
b. 同样,该方程\(y=−1\)只有一个变量,即\(y\)。 的值\(y\)是恒定的。 下表中的所有有序对都具有相同的\(y\)-cordence。 图形是一条穿过\(y\)-axis 的水平线\(−1.\)
| \(\mathbf{x}\) | \(\mathbf{ y}\) | \(\mathbf{(x,y)}\) |
|---|---|---|
| \ (\ mathbf {x}\)” data-valign= “middle” >0 | \ (\ mathbf {y}\)” data-valign= “middle” >\(−1\) | \ (\ mathbf {(x, y)}\)” data-valign= “middle” >\((0,−1)\) |
| \ (\ mathbf {x}\)” data-valign= “middle” >3 | \ (\ mathbf {y}\)” data-valign= “middle” >\(−1\) | \ (\ mathbf {(x, y)}\)” data-valign= “middle” >\((3,−1)\) |
| \ (\ mathbf {x}\)” data-valign= “middle” >\(−3\) | \ (\ mathbf {y}\)” data-valign= “middle” >\(−1\) | \ (\ mathbf {(x, y)}\)” data-valign= “middle” >\((−3,−1)\) |
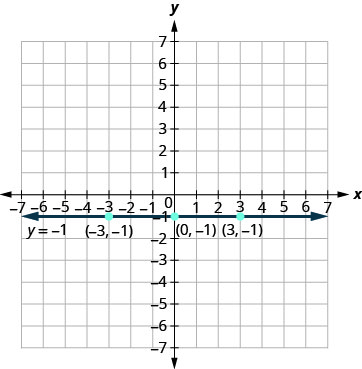
G raph 方程式:a.\(x=5\) b. \(y=−4\).
- 回答
-
一个。
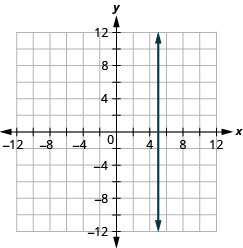
b。
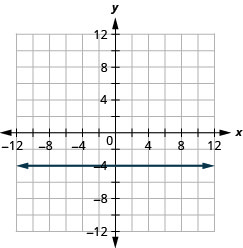
G raph 方程式:a.\(x=−2\) b. \(y=3\).
- 回答
-
一个。
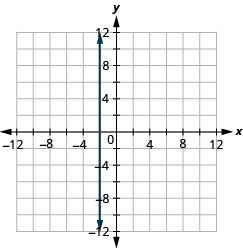
b。
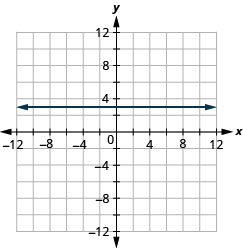
方程和方程有什么区\(y=4x\)别\(y=4\)?
方程既\(y=4x\)有\(x\)又有。\(y.\)的值\(y\)取决于的值,\(x,\)因此\(y\)-坐标会根据的值而变化。\(x.\)方程\(y=4\)只有一个变量。 的值\(y\)是常量,它不依赖于的值,\(x,\)所以\(y\)-坐标始终为\(4.\)
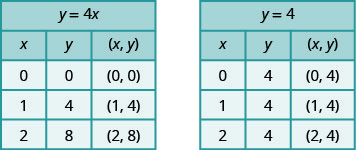
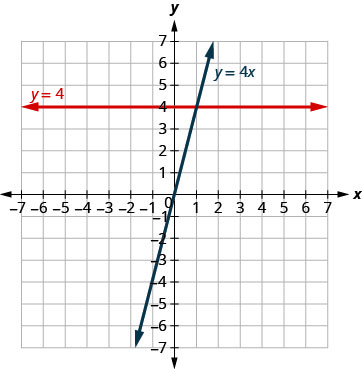
注意,在图表中,方程\(y=4x\)给出了一条倾斜的线,而\(y=4\)给出了一条水平线。
图表\(y=−3x\)和\(y=−3\)在同一个直角坐标系中。
解决方案:
我们注意到第一个方程有变量,\(x,\)而第二个方程没有。 我们为每个方程制作一个点表,然后绘制线条图。 显示了两张图表。
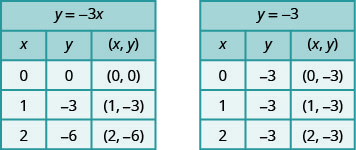
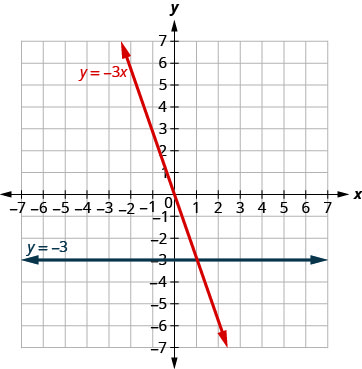
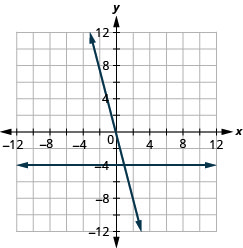
在同一个直角坐标系中绘制方程的图形:\(y=−4x\)和\(y=−4\)。
- 回答
-
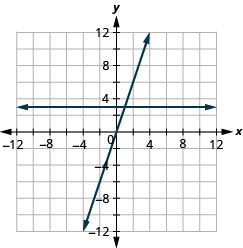
在同一个直角坐标系中绘制方程的图形:\(y=3\)和\(y=3x\)。
- 回答
-
查找\(x\)-和\(y\)-截取
每个线性方程都可以通过一条显示方程所有解的唯一线来表示。 我们已经看到,通过绘制点来绘制线条时,可以使用任意三种解决方案来绘制图形。 这意味着绘制线条的两个人可能会使用不同的三点集。
乍一看,它们的两条线可能看起来不一样,因为它们会标有不同的点。 但是,如果所有工作都正确完成,则线条应该完全相同。 识别它们确实是同一条线的一种方法是查看直线与-a\(x\) xis和-axis的\(y\)交叉位置。 这些点被称为直线的截点。
直线与\(x\)-axis 和-ax\(y\) is 交叉的点称为直线的截点。
让我们来看看线条的图表。
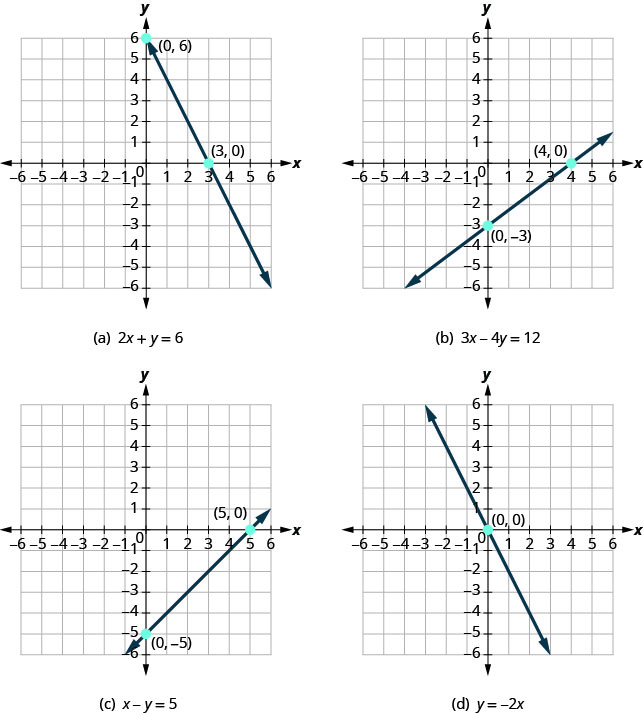
首先,注意每条线与\(x\)-axis交叉的位置。 参见表。
现在,让我们看一下这些直线与\(y\)-axis 交叉的点。
| 图 | 这条线在 以下位置穿过\(x\)-axis |
此积分已订购一对 |
这条线 在以下位置穿过 y 轴: |
此积分已订购一对 |
|---|---|---|---|---|
| 图 (a) | \ (x\)-axis 位于:” data-valign= “middle” >\(3\) | \((3,0)\) | \(6\) | \((0,6)\) |
| 图 (b) | \ (x\)-axis 位于:” data-valign= “middle” >\(4\) | \((4,0)\) | \(−3\) | \((0,−3)\) |
| 图 (c) | \ (x\)-axis 位于:” data-valign= “middle” >\(5\) | \((5,0)\) | \(−5\) | \((0,5)\) |
| 图 (d) | \ (x\)-axis 位于:” data-valign= “middle” >\(0\) | \((0,0)\) | \(0\) | \((0,0)\) |
| 一般人物 | \ (x\)-axis 位于:” data-valign= “middle” >\(a\) | \((a,0)\) | \(b\) | \((0,b)\) |
你看到图案了吗?
对于每条线,直线\(y\)与-a\(x\) xis 交叉点的-坐标为零。 直线与\(x\)-axis 交叉的点的形式为\((a,0)\),称为直线的\(x\) -intercept。 当为零时\(y\),会出现\(x\)-intercept。
在每条线中,直线与\(y\)-axis 交叉点的\(x\) - 坐标为零。 直线与\(y\)-axis 交叉的点的形式为\((0,b)\),称为直线的\(y\) -intercept。 当为零时\(x\),会出现\(y\)-intercept。
\(x\)-截距是直线与\(x\)-axis 交叉的点\((a,0)\)。
\(y\)-截距是直线与\(y\)-axis 交叉的点\((0,b)\)。

在显示的每张图上找到\(x\)-和\(y\)-截距。
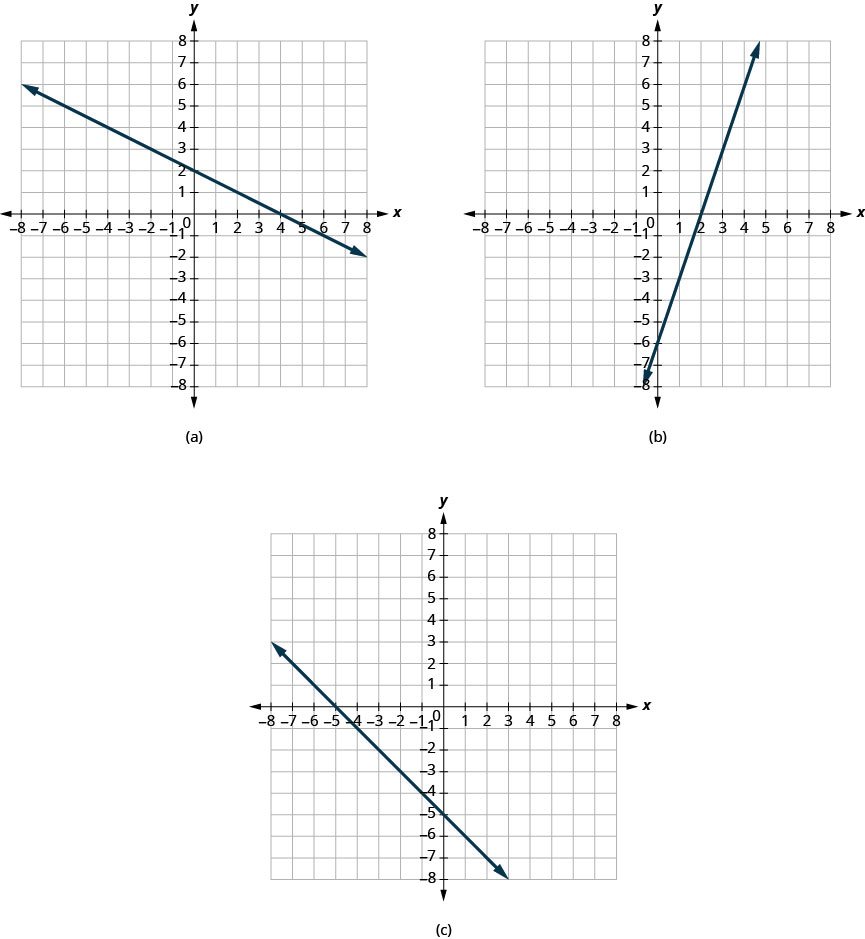
解决方案:
a. 图形在该点处穿过\(x\)-axis\((4,0)\)。 x- 截距为\((4,0)\)。
图形在该点处穿过\(y\)-axis\((0,2)\)。 \(y\)-截距为\((0,2)\)。
b. 图形在该点处穿过\(x\)-axis\((2,0)\)。 \(x\)-截距为\((2,0)\)。
图形在该点处穿过\(y\)-axis\((0,−6)\)。 \(y\)-截距为\((0,−6)\)。
c. 图形在该点处穿过\(x\)-axis\((−5,0)\)。 \(x\)-截距为\((−5,0)\)。
图形在该点处穿过\(y\)-axis\((0,−5)\)。 \(y\)-截距为\((0,−5)\)。
在图表上找到\(x\)-和\(y\)-截距。
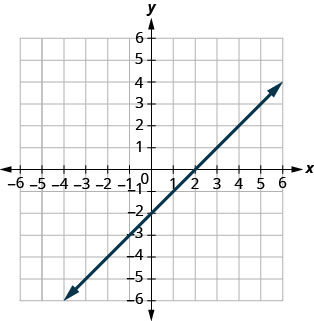
- 回答
-
\(x\)-截距:\((2,0)\),
\(y\)-截距:\((0,−2)\)
在图表上找到\(x\)-和\(y\)-截距。
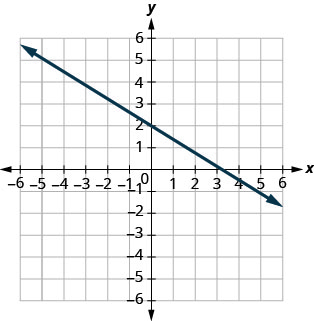
- 回答
-
\(x\)-截距:\((3,0)\),
\(y\)-截距:\((0,2)\)
认识到\(x\) -intercept 在\(y\)为零时发生,\(y\)-intercept 发生在\(x\)为零时,这为我们提供了一种从直线的方程中求出直线的截距的方法。 要找到\(x\)-intercept,让 t\(y=0\) and solve for\(x.\) o 找到\(y\)-intercept,让\(x=0\) and solve for\(y.\)
使用直线方程。 要查找:
- 直线的\(x\)截距,let\(y=0\) 和 solve for\(x\)。
- 直线的\(y\)截距,let\(x=0\) 和 solve for\(y\)。
找到截取的内容\(2x+y=8\)。
解决方案:
我们将让我们\(y=0\)找到\(x\)-截距,然后让我们\(x=0\)找到\(y\)-截距。 我们将填写一张表格,提醒我们我们需要找到什么。

| 要找到\(x\)-截距,让\(y=0\)。 | |
| \(2x+y=8\) | |
| 让\(y=0\)。 | \(2x+{\color{red}0}=8\) |
| 简化。 | \(2x=8\) |
| \(x=4\) | |
| \(x\)-截距为: | \((4,0)\) |
| 要找到\(y\)-截距,让\(x=0\)。 | |
| \(2x+y=8\) | |
| 让\(x=0\)。 | \(2 ( {\color{red}0}) + y = 8\) |
| 简化。 | \(0 + y = 8\) |
| \(y=8\) | |
| \(y\)-截距为: | \((0,8)\) |
截获量是分数\((4,0)\)\((0,8)\),如表所示。
| \(2x+y=8\) | |
| \(x\) | \(y\) |
| 4 | 0 |
| 0 | 8 |
找到截获物:\(3x+y=12\).
- 回答
-
\(x\)-截距:\((4,0)\),
\(y\)-截距:\((0,12)\)
找到截获物:\(x+4y=8\).
- 回答
-
\(x\)-截距:\((8,0)\),
\(y\)-截距:\((0,2)\)
使用截图画一条线
要通过绘制点来绘制线性方程图,您需要找到三个坐标为方程解的点。 你可以使用 x 和 y 截距作为你的三个分数中的两个。 找到拦截点,然后找到第三个点以确保准确性。 确保各点对齐,然后画出直线。 这种方法通常是绘制线条的最快方法。
\(–x+2y=6\)使用截图绘制图表。
解决方案:



使用截图绘制图表:\(x–2y=4\).
- 回答
-
使用截图绘制图表:\(–x+3y=6\).
- 回答
-
此处总结了使用截距绘制线性方程的步骤。
- 找到该行的\(x\)\(y\)-和-截距。
- 假设 y=0y=0 然后求解\(x\)。
- 让 x=0x=0 求解\(y\)。
- 找到方程的第三个解。
- 绘制这三个点并检查它们是否对齐。
- 画出这条线。
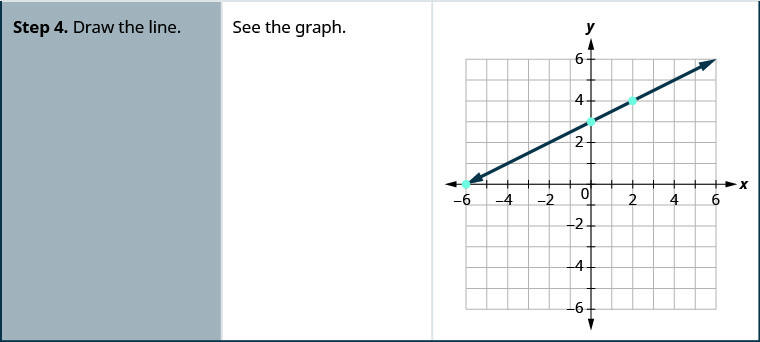
\(4x−3y=12\)使用截图绘制图表。
解决方案:
找到拦截点和第三个点。
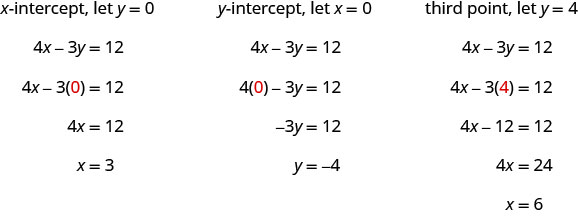
我们在表中列出了点并显示了图表。
| \(4x−3y=12\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| 3 | 0 | \((3,0)\) |
| 0 | \(−4\) | \((0,−4)\) |
| 6 | 4 | \((6,4)\) |
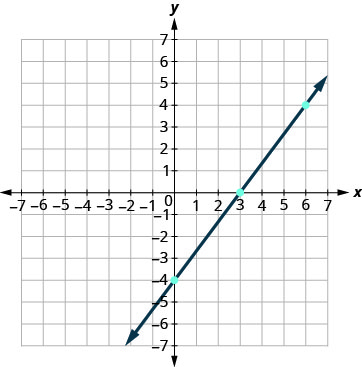
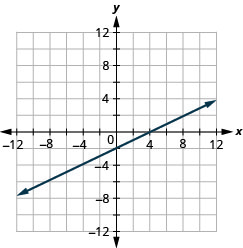
使用截图绘制图表:\(5x−2y=10\).
- 回答
-
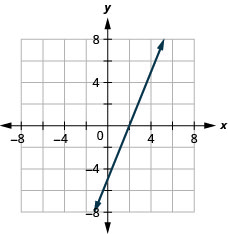
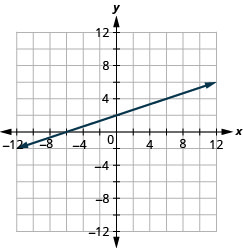
使用截图绘制图表:\(3x−4y=12\).
- 回答
-
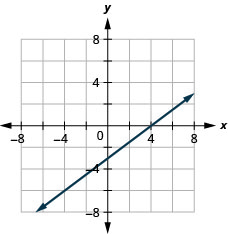
当直线穿过原点时,\(x\)-intercept 和\(y\)-intercept 是同一个点。
\(y=5x\)使用截图绘制图表。
解决方案:

这条线只有一个截距。 这就是重点\((0,0)\)。
为了确保准确性,我们需要绘制三个点。 由于\(x\)-和\(y\)-截距是同一个点,我们需要另外两个点来绘制直线。
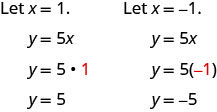
由此产生的三点汇总在表中。
| \(y=5x\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| 0 | 0 | \((0,0)\) |
| 1 | 5 | \((1,5)\) |
| \(−1\) | \(−5\) | \((−1,−5)\) |
绘制三个点,检查它们是否对齐,然后画出直线。
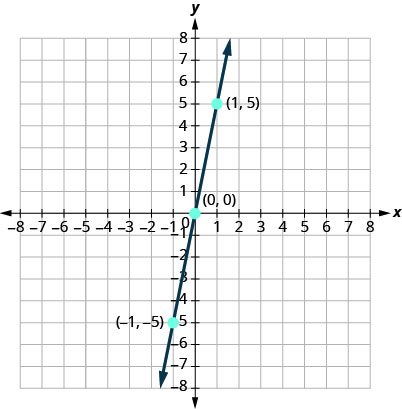
使用截图绘制图表:\(y=4x\).
- 回答
-
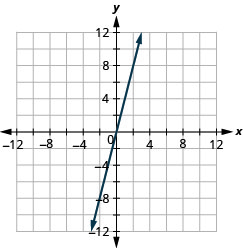
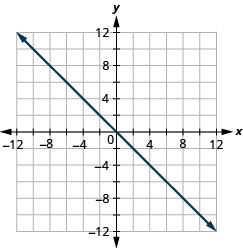
绘制拦截图:\(y=−x\).
- 回答
-
关键概念
- 坐标轴上的点
- \(y\)-坐标等于的点\(0\)位于\(x\)-axis 上,并且有坐标\((a,0)\)。
- \(x\)-坐标等于\(0\)的点位于\(y\)-axis 上,并且有坐标\((0,b)\)。
- 象限
象限 I 象限二 象限三 象限四 \((x,y)\) \((x,y)\) \((x,y)\) \((x,y)\) \((+,+)\) \((-,+)\) \((-,-)\) \((+,-)\) 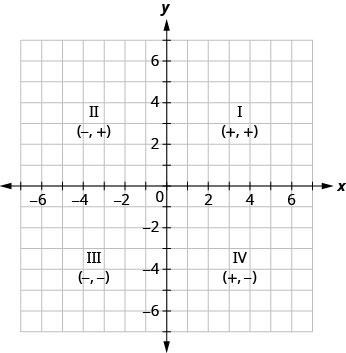
- 线性方程图:线性方程的图形\(Ax+By=C\)是一条直线。
直线上的每个点都是方程的解。
这个方程的每个解都是这条线上的一个点。 - 如何通过绘制点来绘制线性方程。
- 找出坐标为方程解的三个点。 将它们整理在桌子里。
- 在矩形坐标系中绘制点。 检查各点是否对齐。 如果没有,请仔细检查你的工作。
- 画一条穿过这三个点的直线。 延伸线条以填充网格,并在直线的两端放置箭头。
- \(x\)-截距和\(y\)-截距
- \(x\)-截距是直线与\(x\)-axis 交叉的点\((a,0)\)。
- \(y\)-截距是直线与\(y\)-axis 交叉的点\((0,b)\)。

- 从直线方程中找\(y\)出\(x\)-和-截距
- 使用直线方程。 找到:
直线的\(x\)-截距,le\(y=0\) t and\(y\) solve 求\(x.\)
解直线的截距,le\(x=0\) t and solve\(y.\)
- 使用直线方程。 找到:
- 如何使用截距绘制线性方程。
- 找到该行的\(x\)\(y\)-和-截距。
Let\(y=0\) and solve\(x.\)
for Let\(x=0\) 然后求解\(y.\) - 找到方程的第三个解。
- 绘制这三个点并检查它们是否对齐。
- 画出这条线。
- 找到该行的\(x\)\(y\)-和-截距。
词汇表
- 水平线
- 水平线是方程的图形,其形式\(y=b.\)为:直线穿过\(y\)-axis\((0,b).\)
- 直线的截取次数
- 直线与\(x\)-axis 和-ax\(y\) is 交叉的点称为直线的截点。
- 线性方程
- 形式\(Ax+By=C,\)为\(A\)且不\(B\)均为零的方程称为由两个变量组成的线性方程。
- 已订购一对
- 有序对\((x,y),\)给出矩形坐标系中一个点的坐标。 第一个数字是\(x\)-坐标。 第二个数字是\(y\)-坐标。
- 起源
- 该点\((0,0)\)被称为原点。 这是\(x\)-axis 和\(y\)-axis 相交的点。
- 两个变量中线性方程的解
- \(Ax+By=C,\)如果将有序对\((x,y)\)的\(x\)-和\(y\)-值替换到方程中时,方程为真陈述,则有序对就是线性方程的解。
- 线性方程的标准形式
- 线性方程在书写时采用标准形式\(Ax+By=C.\)
- 垂直线
- 垂直线是方程的图形,其形式\(x=a.\)为:直线穿过\(x\)-axis\((a,0).\)


