2.2:使用通用策略求解线性方程
- Page ID
- 204193
在本节结束时,您将能够:
- 使用交换和关联属性
- 使用恒等式、反向和零的属性
- 使用分布属性简化表达式
在开始之前,请参加这个准备测验。
- 简化:\(\frac{3}{2}(12x+20)\)。
- 简化:\(5−2(n+1)\)。
- 找到\(\frac{5}{6}\)和的液晶屏\(\frac{1}{4}\)。
使用一般策略求解线性方程
求解方程就像发现谜题的答案。 求解方程的目的是找到使其成为真实陈述的一个或多个变量的值。 使方程成真的变量的任何值都称为方程解。 这是拼图的答案!
方程的解是一个变量的值,当它被替换到方程中时,该变量的陈述是真实的。
为了确定一个数字是否是方程的解,我们用该值代替方程中的变量。 如果得到的方程是真实的陈述,则数字是方程的解。
- 用数字代替方程中的变量。
- 简化方程两边的表达式。
- 确定所得方程是否正确。
- 如果是真的,那么这个数字就是一个解。
- 如果不是,则该数字不是解决方案。
确定这些值是否为方程的解:\(5y+3=10y−4\).
- \(y=\frac{3}{5}\)
- \(y=\frac{7}{5}\)
由于方程的解是使方程成真的变量的值,因此首先用解的值代替变量。
一个。
| \(5 y+3=10 y-4\) | |
| 替代\(\color{rec}\frac{3}{5}\)\(y\) | \(5\left( \color{red} \frac{3}{5} \color{black}\right)+3 \stackrel{?}{=} 10\left( \color{red}\frac{3}{5} \color{black}\right)-4\) |
| 乘。 | \(3+3\stackrel{?}{=} 6-4\) |
| 简化。 | \(6 \neq 2\) |
因为\(y=\frac{3}{5}\)没有得出真正的方程,所以\(y=\frac{3}{5}\)不是方程的解\(5y+3=10y−4.\)
b。
| \(5 y+3=10 y-4\) | |
| 替代\(\color{red} \frac{7}{5}\)\(y\) | \(5\left(\color{red} \frac{7}{5} \color{black}\right)+3 \stackrel{?}{=} 10\left(\color{red}\frac{7}{5}\color{back}\right)-4\) |
| 乘。 | \(7+3 \stackrel{?}{=} 14-4\) |
| 简化。 | \(10=10 \checkmark\) |
由于\(y=\frac{7}{5}\)结果为真方程,\(y=\frac{7}{5}\)因此是方程的解\(5y+3=10y−4.\)
确定这些值是否为方程的解:\(9y+2=6y+3.\)
- \(y=\frac{4}{3}\)
- \(y=\frac{1}{3}\)
- 回答 a
-
不
- 答案 b
-
是的
确定这些值是否为方程的解:\(4x−2=2x+1\).
- \(x=\frac{3}{2}\)
- \(x=−\frac{1}{2}\)
- 回答 a
-
是的
- 答案 b
-
不
我们将学会求解许多类型的方程式。 在本节中,我们将重点介绍线性方程。
线性方程是一个变量中的方程,可以写出来,其中\(a\)和\(b\)是实数\(a≠0\),如下所示:
\[ax+b=0\]
要求解线性方程,最好有一个可用于求解任何线性方程的总体策略。 在下一个示例中,我们将给出求解任何线性方程的通用策略的步骤。 首先尽可能简化方程的每一面,可以更轻松地完成其余步骤。
解决:\(7(n−3)−8=−15\)
- 回答
-




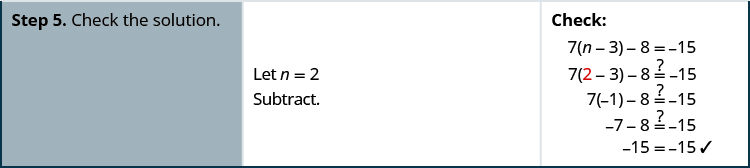
解决:\(2(m−4)+3=−1.\)
- 回答
-
\(m=2\)
解决:\(5(a−3)+5=−10.\)
- 回答
-
\(a=0\)
这些步骤在下面的求解线性方程的通用策略中进行了总结。
- 尽可能简化方程的每一面。
使用分布属性删除所有括号。
将相似的术语组合在一起。 - 收集方程一侧的所有变量项。
使用等式的加法或减法属性。
- 收集方程另一侧的所有常量项。
使用等式的加法或减法属性。
- 使变量项的系数等于 1。
使用等式的乘法或除法属性。
陈述方程的解。
- 检查解决方案。
将解替换为原始方程以确保结果是真实的陈述。
解决:\(\frac{2}{3}(3m−6)=5−m\)。
- 回答
-
\(\frac{2}{3}(3 m-6)=5-m\) 分发。 \(2 m-4=5-m\) \(m\)将两边相加,只得到左边的变量。 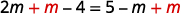
简化。 \(3 m-4=5\) \(4\)将两边相加,只获得右边的常量。 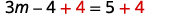
简化。 \(3 m=9\) 将两边除以三。 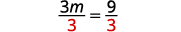
简化。 \(m=3\)
| 查看: | 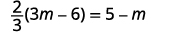 |
| 让\(m=3\)。 | 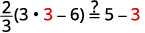 |
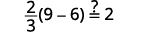 |
|
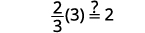 |
|
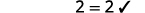 |
解决:\(\frac{1}{3}(6u+3)=7−u\)。
- 回答
-
\(u=2\)
解决:\(\frac{2}{3}(9x−12)=8+2x\)。
- 回答
-
\(x=4\)
我们可以通过将所有变量项放在等号的任一侧来求解方程。 通过在变量系数较大的一侧收集变量项,我们可以避免使用一些负数。 当我们在本章后面解决不平等问题时,这将是一个不错的策略。 它还可以帮助我们防止负面错误。
解决:\(4(x−1)−2=5(2x+3)+6\)。
- 回答
-
\(4(x-1)-2=5(2 x+3)+6\) 分发。 \(4 x-4-2=10 x+15+6\)
将相似的术语组合在一起。 \(4 x-6=10 x+21\) \(4x\)从两边减去以后只能得到右边的变量\(10>4\)。 \(4 x \color{red} -4 \color{black} x-6=10 x \color{red}-4 x \color{black}+21\) 简化。 \(-6=6 x+21\) \(21\)从两边减去得到左边的常量。 \(-6 \color{red} -21 \color{black} =6 x+21 \color{red}-21\)
简化。 \(-27=6 x\) 将两边除以\(6\)。 \(\frac{-27}{\color{red}6} \color{black}=\frac{6 x}{\color{red}6}\) 简化。 \(-\frac{9}{2}=x\) 查看: \(4(x-1)-2=5(2 x+3)+6\)\) 让\(x=−92\)。 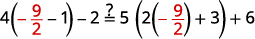
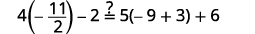
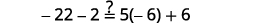
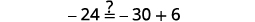
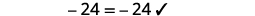
解决:\(6(p−3)−7=5(4p+3)−12.\)
- 回答
-
\(p=−2\)
解决:\(8(q+1)−5=3(2q−4)−1.\)
- 回答
-
\(q=−8\)
解决:\(10[3−8(2s−5)]=15(40−5s)\)。
- 回答
-
\(10[3-8(2 s-5)]=15(40-5 s)\) 首先从最里面的圆括号中进行简化。 \(10[3-16 s+40]=15(40-5 s)\) 在方括号中组合相似的术语。 \(10[43-16 s]=15(40-5 s)\) 分发。 \(430-160 s=600-75 s\) \(160s\)将两边相加,\(160s\)使两边都加上,使变量向右。 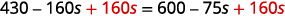
简化。 \(430=600+85 s\) \(600\)从两边减去将常量放在左边。 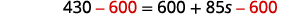
简化。 \(-170=85 s\) 将两边除以\(85\)。 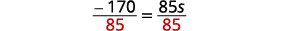
简化。 \(-2=s,\)所以\(s = -2\) 查看: \(10[3-8(2 s-5)]=15(40-5 s)\) 让\(s=−2\)。 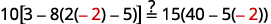
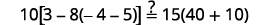
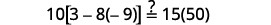
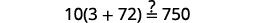
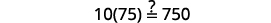
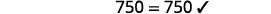
解决:\(6[4−2(7y−1)]=8(13−8y)\)。
- 回答
-
\(y=−\frac{17}{5}\)
解决:\(12[1−5(4z−1)]=3(24+11z).\)
- 回答
-
\(z=0\)
对方程进行分类
方程是否为真取决于变量的值。 当我们用\(7x+8=−13\)值替换变量 x 时,方程为真\(−3\),但当我们用任何其他值替换 x 时,方程不正确。 像这样的方程被称为条件方程。 到目前为止,我们求解的所有方程都是条件方程。
如果变量的一个或多个值为 true,而变量的所有其他值均为 false 的方程即为条件方程。
现在让我们考虑这个方程式\(7y+14=7(y+2)\)。 你知道左边和右边是等同的吗? 让我们看看当我们求解 y 时会发生什么。
解决:
| \(7 y+14=7(y+2)\) | |
| 分发。 | \(7 y+14=7 y+14\) |
| 减\(7y\)去每一边,使\(y’\) s变为一边。 | \(7 y \color{red}-7 y \color{black} +14=7 y \color{red} -7 y \color{black}+14\) |
| 简化 —\(y\) — 被淘汰了。 | \(14=14\) |
| 但\(14=14\)确实如此。 |
这意味着,对于任何值\(7y+14=7(y+2)\),该方程都是正确的\(y\)。 我们说方程的解是所有的实数。 对于变量的任何值都正确的方程称为恒等式。
对于变量的任何值都正确的方程称为恒等式。
标识解对所有实数都有效。
当我们求解方程时会发生什么\(−8z=−8z+9?\)
解决:
| \(-8 z=-8 z+9\) | |
| 两边\(8z\)相加,将常数单独留在右边。 | \(-8 z \color{red} +8 z \color{black}=-8 z \color{red}+8 z \color{black} +9\) |
| 简化 —\(z\) — 被淘汰了。 | \(0 \neq 9\) |
| 但是\(0≠9\)。 |
求解方程\(−8z=−8z+9\)导致了错误的陈述\(0=9\)。 对于任何值,该方程\(−8z=−8z+9\)都不成立\(z\)。 它没有解决办法。 没有解的方程或变量的所有值均为假的方程称为矛盾。
对于变量的所有值都为假的方程称为矛盾。
矛盾没有解决办法。
接下来的几个例子将要求我们将方程分为条件方程、恒等式或矛盾方程。
将方程归类为条件方程、恒等式或矛盾,然后陈述解:\(6(2n−1)+3=2n−8+5(2n+1)\)。
- 回答
-
\(6(2 n-1)+3=2 n-8+5(2 n+1)\) 分发。 \(12 n-6+3=2 n-8+10 n+5\) 将相似的术语组合在一起。 \(12 n-3=12 n-3\) \(12n\)从两边减去,得到\(n\) s 为一边。 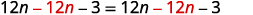
简化。 \(-3=-3\) 这是真实的陈述。 方程是一个恒等式。 解决方案都是实数。
将方程归类为条件方程、恒等方程或矛盾方程,然后陈述解:\(4+9(3x−7)=−42x−13+23(3x−2).\)
- 回答
-
身份;所有实数
将方程归类为条件方程、恒等方程或矛盾方程,然后陈述解:\(8(1−3x)+15(2x+7)=2(x+50)+4(x+3)+1.\)
- 回答
-
身份;所有实数
将方程归类为条件方程、恒等式或矛盾,然后陈述解:\(8+3(a−4)=0\)。
- 回答
-
\(8+3(a-4)=0\) 分发。 \(8+3 a-12=0\) 将相似的术语组合在一起。 \(3 a-4=0\) \(4\)添加到两边。 \(3 a-4 \color{red}+4 \color{black}=0 \color{red}+4\) 简化。 \(3 a=4\) 除以。 \(\frac{3 a}{\color{red}3} \color{black}=\frac{4}{\color{red}3}\) 简化。 \(a=\frac{4}{3}\) 等式在以下情况下是正确的\(a=\frac{4}{3}\)。 这是一个条件方程。 解决方案是\(a=\frac{4}{3}\)。
将方程归类为条件方程、恒等式或矛盾,然后陈述解:\(11(q+3)−5=19\)。
- 回答
-
条件方程;\(q=−\frac{9}{11}\)
将方程归类为条件方程、恒等式或矛盾,然后陈述解:\(6+14(k−8)=95\)。
- 回答
-
条件方程;\(k=\frac{201}{14}\)
将方程归类为条件方程、恒等式或矛盾,然后陈述解:\(5m+3(9+3m)=2(7m−11)\)。
- 回答
-
\(5 m+3(9+3 m)=2(7 m-11)\) 分发。 \(5 m+27+9 m=14 m-22\) 将相似的术语组合在一起。 \(14 m+27=14 m-22\) \(14m\)从两边减去。 \(14 m+27 \color{red}-14 m \color{black}=14 m-22 \color{red}-14 m\) 简化。 \(27 \neq-22\) 但是\(27≠−22\)。 这个方程式是矛盾的。 它没有解决办法。
将方程归类为条件方程、恒等式或矛盾,然后陈述解:\(12c+5(5+3c)=3(9c−4)\)。
- 回答
-
矛盾;没有解决办法
将方程归类为条件方程、恒等式或矛盾,然后陈述解:\(4(7d+18)=13(3d−2)−11d\)。
- 回答
-
矛盾;没有解决办法
我们在表中总结了对方程进行分类的方法。
| 方程的类型 | 当你解决这个问题时会发生什么? | 解决方案 |
|---|---|---|
| 条件方程 | 变量的一个或多个值为 true,所有其他值为 false | 一个或多个值 |
| 身份 | 变量的任何值均为 true | 所有实数 |
| 矛盾 | 变量的所有值均为 False | 没有解决办法 |
使用分数或十进制系数求解方程
我们可以使用通用策略来解决下一个例子。 这种方法可以正常工作,但是许多学生在看到所有这些分数时并不感到非常自信。 因此,我们将展示一种用分数求解方程的另一种方法。 这种替代方法消除了分数。
我们将应用相等的乘法属性,将方程的两边乘以方程中所有分数的最小公分母 (LCD)。 此运算的结果将是一个新方程,等同于第一个方程,但没有分数。 这个过程称为清除分数方程。
为了清除小数方程,我们以分数形式考虑所有小数,然后找到这些分母的 LCD。
解决:\(\frac{1}{12}x+\frac{5}{6}=\frac{3}{4}\)。
- 回答
-



解决:\(\frac{1}{4}x+\frac{1}{2}=\frac{5}{8}\)。
- 回答
-
\(x=\frac{1}{2}\)
解决:\(\frac{1}{8}x+\frac{1}{2}=\frac{1}{4}\)。
- 回答
-
\(x=−2\)
请注意,在前面的示例中,一旦我们清除了分数方程,该方程就像我们在本章前面求解的方程一样。 我们将问题改为已经知道如何解决的问题。 然后,我们使用了求解线性方程的通用策略。
- 找出方程中所有分数和小数(以分数形式)中的最小公分母 (LCD)。
- 将方程的两边乘以该液晶屏。 这会清除分数和小数。
- 使用求解线性方程的通用策略进行求解。
解决:\(5=\frac{1}{2}y+\frac{2}{3}y−\frac{3}{4}y\)。
- 回答
-
我们想通过将方程的两边乘以方程中所有分数的液晶显示屏来清除分数。
找到方程中所有分数的 LCD。 \(5=\frac{1}{2} y+\frac{2}{3} y-\frac{3}{4} y\) 液晶屏是\(12\)。 将方程的两边乘以\(12\)。 \(\color{red}12 \color{black}(5)=\color{red}12 \color{black} \cdot\left(\frac{1}{2} y+\frac{2}{3} y-\frac{3}{4} y\right)\) 分发。 \(12(5)=12 \cdot \frac{1}{2} y+12 \cdot \frac{2}{3} y-12 \cdot \frac{3}{4} y\) 简化-注意,不要再有分数了。 \(60=6 y+8 y-9 y\) 将相似的术语组合在一起。 \(60=5 y\) 除以五。 \(\frac{60}{\color{red}5} \color{black}=\frac{5 y}{\color{red}5}\) 简化。 \(12=y\) 查看: \(5=\frac{1}{2} y+\frac{2}{3} y-\frac{3}{4} y\) 让\(y=12\)。 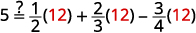
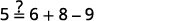

解决:\(7=\frac{1}{2}x+\frac{3}{4}x−\frac{2}{3}x\)。
- 回答
-
\(x=12\)
解决:\(−1=\frac{1}{2}u+\frac{1}{4}u−\frac{2}{3}u\)。
- 回答
-
\(u=−12\)
在下一个示例中,我们将在清除分数之前进行分布。
解决:\(\frac{1}{2}(y−5)=\frac{1}{4}(y−1)\)。
- 回答
-
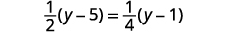
分发。 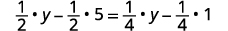
简化。 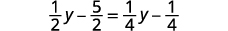
乘以液晶屏,四。 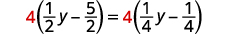
分发。 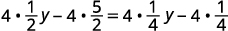
简化。 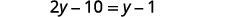
收集左边的变量。 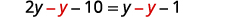
简化。 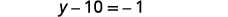
收集右边的常量。 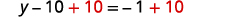
简化。 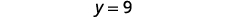
求解这个方程的另一种方法是清除分数而不先分布。 如果正确地将因子相乘,则此方法会更容易。 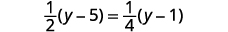
乘以液晶屏,\(4\)。 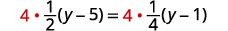
将分数乘以四倍。 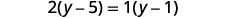
分发。 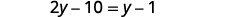
收集左边的变量。 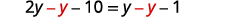.jpg)
简化。 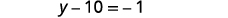
收集右边的常量。 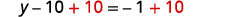
简化。 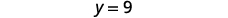
查看: 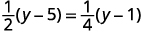
让\(y=9\)。 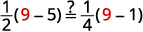
自己完成支票。
解决:\(\frac{1}{5}(n+3)=\frac{1}{4}(n+2)\)。
- 回答
-
\(n=2\)
解决:\(\frac{1}{2}(m−3)=\frac{1}{4}(m−7)\)。
- 回答
-
\(m=−1\)
将方程的两边乘以分数的 LCD 时,确保将每个项乘以 LCD,即使它不包含分数。
解决:\(\frac{4q+3}{2}+6=\frac{3q+5}{4}\)
- 回答
-
\(\frac{4 q+3}{2}+6=\frac{3 q+5}{4}\) 将两边乘以液晶屏,\(4\)。 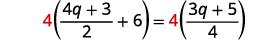
分发。 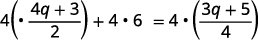
简化。 \(2(4 q+3)+24=3 q+5\) \(8 q+6+24=3 q+5\) \(8 q+30=3 q+5\) 收集左边的变量。 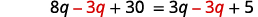
简化。 \(5 q+30=5\) 收集右边的常量。 
简化。 \(5 q=-25\) 将两边除以五。 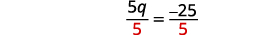
简化。 \(q=-5\) 查看: \(\frac{4 q+3}{2}+6=\frac{3 q+5}{4}\) 让\(q=−5.\) 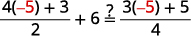
自己完成支票。
解决:\(\frac{3r+5}{6}+1=\frac{4r+3}{3}\)。
- 回答
-
\(r=3\)
解决:\(\frac{2s+3}{2}+1=\frac{3s+2}{4}\)。
- 回答
-
\(s=−8\)
有些方程中有小数。 当我们解决处理金钱或百分比的问题时,可能会出现这种方程式。 但是小数也可以表示为分数。 例如,\(0.7=\frac{7}{10}\)和\(0.29=\frac{29}{100}\)。 因此,对于带小数的方程,我们可以使用与清除分数相同的方法——将方程的两边乘以最小公分母。
下一个例子使用了一个典型的方程式,我们将在后面的货币应用程序中看到这个方程式。 请注意,我们将通过乘以分数形式的 LCD 来清除所有小数。
解决:\(0.25x+0.05(x+3)=2.85\)。
- 回答
-
看看小数,想想等效的分数:
\[0.25=\frac{25}{100}, \; \; \; \;\;\;\;\; 0.05=\frac{5}{100}, \;\;\;\;\;\;\;\; 2.85=2\frac{85}{100}.\]
注意,液晶屏是\(100\)。 通过乘以液晶显示器,我们将清除方程中的小数。
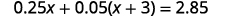
先分发。 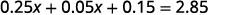
将相似的术语组合在一起。 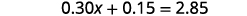
要清除小数,请乘以\(100\)。 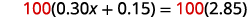
分发。 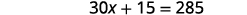
\(15\)从两边减去。 
简化。 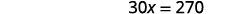
除以\(30\)。 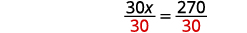
简化。 
代\(x=9\)入原始方程式,自己检查一下。
解决:\(0.25n+0.05(n+5)=2.95.\)
- 回答
-
\(n=9\)
解决:\(0.10d+0.05(d−5)=2.15.\)
- 回答
-
\(d=16\)
关键概念
- 如何确定一个数字是否是方程的解
- 用数字代替方程中的变量。
- 简化方程两边的表达式。
- 确定所得方程是否正确。
如果是真的,那么这个数字就是一个解。
如果不是,则该数字不是解决方案。
- 如何使用通用策略求解线性方程
- 尽可能简化方程的每一面。
使用分布属性删除所有括号。
将相似的术语组合在一起。
- 收集方程一侧的所有变量项。
使用等式的加法或减法属性。
- 收集方程另一侧的所有常量项。
使用等式的加法或减法属性。
- 使变量项的系数等于 1。
使用等式的乘法或除法属性。
陈述方程的解。
- 检查解决方案。
将解替换为原始方程以确保结果是真实的陈述。
- 尽可能简化方程的每一面。
- 如何用分数或十进制系数求解方程
- 找出方程中所有分数和小数(以分数形式)中的最小公分母 (LCD)。
- 将方程的两边乘以该液晶屏。 这会清除分数和小数。
- 使用求解线性方程的通用策略进行求解。
词汇表
- 条件方程
- 如果变量的一个或多个值为 true,而变量的所有其他值均为 false 的方程即为条件方程。
- 矛盾
- 对于变量的所有值都为假的方程称为矛盾。 矛盾没有解决办法。
- 身份
- 对于变量的任何值都正确的方程称为身份。 一个恒等的解是全实数。
- 线性方程
- 线性方程是一个可以写入的变量中的方程,其中 a 和 b 是实数\(a≠0\),as\(ax+b=0\)。
- 方程的解
- 方程的解是一个变量的值,当它被替换到方程中时,该变量的陈述是真实的。


