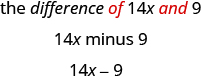1.2: 使用代数语言
- Page ID
- 203943
在本节结束时,您将能够:
- 查找因子、素数分解和最小公倍数
- 使用变量和代数符号
- 使用运算顺序简化表达式
- 计算表达式
- 识别并合并相似的术语
- 将英语短语翻译成代数表达式
本章旨在简要回顾中级代数课程所需的概念。 对本章所涵盖主题的更详尽的介绍可以在基本代数章节 “基础” 中找到。
查找因子、素数分解和最小公倍数
数字 2、4、6、8、10、12 被称为 2 的倍数。 2 的倍数可以写成计数数字和 2 的乘积。
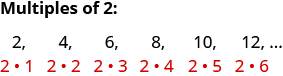
同样,3 的倍数将是计数数字和 3 的乘积。

通过继续这个过程,我们可以找到任何数字的倍数。
| 计数数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 的倍数 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| 3 的倍数 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| 4 的倍数 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| 5 的倍数 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| 6 的倍数 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| 7 的倍数 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| 8 的倍数 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| 9 的倍数 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
\(n\)如果数字是计数数字的乘积,则数字是的倍数\(n\)。
说15是3的倍数的另一种方法是说15可以被3 整除。 这意味着当我们将 3 除以 15 时,我们得到一个计数数字。 实际上,\(15÷3\)是\(5\),也\(15\)是\(5⋅3\)。
如果一个数字\(m\)是的倍数\(n\),\(m\)则可被整除\(n\)。
如果我们要寻找数字 2 到 9 的倍数中的模式,我们会发现以下可除性测试:
一个数字可以整除为:
- 如果最后一位数字为 0、2、4、6 或 8,则为 2。
- 如果数字之和可被 3 整除,则为 3。
- 如果最后一位数字为 5 或 0,则为 5。
- 如果它可以被 2 和 3 整除,则为 6。
- 如果以 0 结尾,则为 10。
5,625 可以被整除吗
- 2?
- 3?
- 5 还是 10?
- 6?
- 回答
-
一个。
\(\text{Is 5,625 divisible by 2?}\)
\( \begin{array}{ll} \text{Does it end in 0, 2, 4, 6 or 8?} & {\text{No.} \\ \text{5,625 is not divisible by 2.}} \end{array}\) - b。
\(\text{5,625 divisible by 3?}\)
\(\begin{array}{ll} {\text{What is the sum of the digits?} \\ \text{Is the sum divisible by 3?}} & {5+6+2+5=18 \\ \text{Yes.} \\ \text{5,625 is divisible by 3.}}\end{array}\) - c。
\(\text{Is 5,625 divisible by 5 or 10?}\)
\(\begin{array}{ll} \text{What is the last digit? It is 5.} & \text{5,625 is divisible by 5 but not by 10.} \end{array}\)d。\(\text{Is 5,625 divisible by 6?}\)
\(\begin{array}{ll}\text{Is it divisible by both 2 and 3?} & {\text{No, 5,625 is not divisible by 2, so 5,625 is} \\ \text{not divisible by 6.}} \end{array}\)
4,962 可以被 a. 2 整除吗? b. 3? c. 5? d. 6? e. 10?
- 回答
-
a. 是的 b. 是的 c. 不 d. 是的 e. 不
3,765 可以被 a. 2 整除吗? b. 3? c. 5? d. 6? e. 10?
- 回答
-
a.no b. 是的 c. 是的 d.no e.
在数学中,通常有几种方法可以谈论相同的想法。 到目前为止,我们已经看到,如果\(m\)是的倍\(n\)数,我们可以说\(m\)它是可以整除的\(n\)。 例如,由于 72 是 8 的倍数,我们说 72 可被 8 整除。 由于 72 是 9 的倍数,我们说 72 可以被 9 整除。 我们可以用另一种方式来表达。
因为\(8·9=72\),我们说8和9是72的因子。 当我们写作时\(72=8·9\),我们说我们已经考虑了72因子。
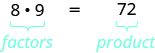
其他考虑方法\(72\)是\(1·72, \; 2·36, \; 3·24, \; 4·18,\)和\(6⋅12\)。 数字 72 有很多因素:\(1,\,2,\,3,\,4,\,6,\,8,\,9,\,12,\,18,\,24,\,36,\)和\(72\)。
如果\(a\)和\(b\)在计算数字\(a·b=m\),那么\(a\)和\(b\)是因子\(m\)。
有些数字,例如72,有许多因子。 其他数字只有两个因子。 素数是大于 1 的计数数,其唯一因子为 1 及其本身。
质数是大于 1 的计数数,其唯一因子为 1 和数字本身。
复合数是非素数的计数数。 复合数除了 1 和数字本身之外的因子。
表中列出了从 2 到 20 的计数数字及其因子。 请务必同意每种标签的 “主要” 或 “复合” 标签!
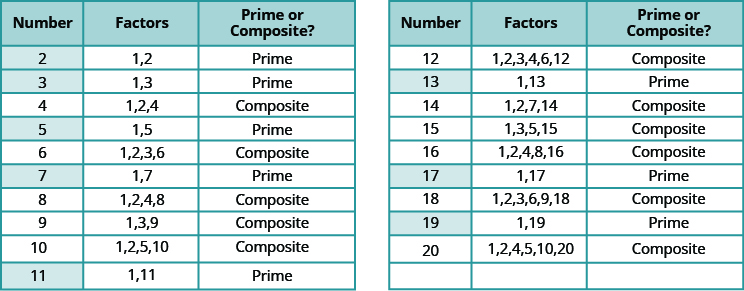
小于 20 的素数为 2、3、5、7、11、13、17 和 19。 请注意,唯一的偶数素数是 2。
复合数可以写成素数的唯一乘积。 这称为数字的素数分解。 在本课程的许多主题中,找到复合数的素数分解将很有用。
数字的素数分解是等于该数字的质数的乘积。
要找到复合数的素数分解,请找到该数字的任意两个因子并使用它们来创建两个分支。 如果一个因子是素数,则该分支是完整的。 圈出那个素数。 否则很容易忘记素数。
如果该因子不是素数,请找到该数的两个因子并继续该过程。 一旦所有分支的末尾都有圈出素数,分解就完成了。 复合数现在可以写成素数的乘积。
因子 48。
- 回答
-


.jpg)
我们说\(2⋅2⋅2⋅2⋅3\)的是 48 的素数因式分解。 我们通常按升序写入素数。 一定要乘以因子来验证你的答案。 \(2⋅2⋅2⋅2⋅3\)是 48 的素数分解。 我们通常按升序写入素数。 一定要乘以因子来验证你的答案。
如果我们首先以不同的方式分解 48,例如 as\(6·8\),则结果仍然是一样的。 完成素数分解并亲自验证。
找到的素数因式分解\(80\)。
- 回答
-
\(2⋅2⋅2⋅2⋅5\)
找到的素数因式分解\(60\)。
- 回答
-
\(2⋅2⋅3⋅5\)
- 找出乘积为给定数字的两个因子,然后使用这些数字创建两个分支。
- 如果一个因子是素数,则该分支是完整的。 环绕素数,就像树上的一片树叶一样。
- 如果一个因子不是素数,则将其写成两个因子的乘积并继续该过程。
- 将复合数写成所有圈出素数的乘积。
我们研究素数的原因之一是使用这些技术来找出两个数中最不常见的倍数。 当我们加上和减去具有不同分母的分数时,这将很有用。
两个数字的最小公倍数 (LCM) 是两个数字的倍数的最小数字。
为了找出两个数字中的最小公倍数,我们将使用素因子法。 让我们使用它们的素数来找出 12 和 18 的 LCM。
使用素数法找出 12 和 18 的最小公倍数 (LCM)。
- 回答
-

.jpg)


请注意,LCM 中包含 12 的素因子\((2·2·3)\)和 18\((2⋅3⋅3)\) 的素因子\((2·2·3·3)\)。 因此,36 是 12 和 18 中最不常见的倍数。
通过匹配常见素数,每个公共素数只能使用一次。 这样你就可以确定36是最不常见的倍数。
使用素数法求出 9 和 12 的 LCM。
- 回答
-
36
使用素数法求出 18 和 24 的 LCM。
- 回答
-
72
- 将每个数字写成素数的乘积。
- 列出每个数字的素数。 尽可能垂直匹配素数。
- 把柱子放下。
- 将因子相乘。
使用变量和代数符号
在代数中,我们使用字母表中的字母来表示其值可能会改变的数字。 我们称之为变量,变量常用的字母是\(x,\,y,\,a,\,b,\)和\(c.\)
变量是一个字母,它代表一个数值,该数字的值可能会改变。
值始终保持不变的数字称为常量。
常量是一个数值,其值始终保持不变。
要用代数书写,我们需要一些运算符号以及数字和变量。 我们将使用几种类型的符号。 有四种基本的算术运算:加法、减法、乘法和除法。 我们将在下面列出用于表示这些操作的符号。
| 操作 | 符号 | 说: | 结果是... |
|---|---|---|---|
| 加法 | \(a+b\) | \(a\)再加上\(b\) | \(a\)和的总和\(b\) |
| 减法 | \(a−b\) | \(a\)减去\(b\) | \(a\)和的区别\(b\) |
| 乘法 | \(a⋅b,\,ab,\,(a)(b),\,(a)b,\,a(b)\) | \(a\)倍\(b\) | \(a\)和的乘积\(b\) |
| 部门 | \(a÷b,\,\space a/b,\,\space\frac{a}{b},\,\space b \overline{\smash{)}a}\) | \(a\)除以\(b\) | and\(b\);\(a\) 的商 \(a\)称为分红,\(b\)被称为除数 |
当两个数量具有相同值时,我们说它们相等,并用等号将它们连接起来。
\(a=b\)读取 “等\(a\)于”\(b\)。
符号 “\(=\)” 被称为等号。
在数字行上,数字从左向右移动时会变大。 数字行可以用来解释符号 “\(<\)” 和 “\(>\)”。

表达式\(a<b\)或\(a>b\)可以从左到右或从右到左阅读,但在英语中,我们通常从左到右阅读。 一般来说,
\[a<b \text{ is equivalent to }b>a. \text{For example, } 7<11 \text{ is equivalent to }11>7.\]
\[a>b \text{ is equivalent to }b<a. \text{For example, } 17>4 \text{ is equivalent to }4<17.\]
| 不等式符号 | 单词 |
|---|---|
| \(a\neq b\) | \(a\)不等于\(b\)。 |
| \(a<b\) | \(a\)小于\(b\)。 |
| \(a\leq b\) | \(a\)小于或等于\(b\)。 |
| \(a>b\) | \(a\)大于\(b\)。 |
| \(a\geq b\) | \(a\)大于或等于\(b\)。 |
对代数中的符号进行分组与英语中的逗号、冒号和其他标点符号非常相似。 它们有助于识别表达式,该表达式可以由数字、变量或使用运算符号的数字和变量组合组成。 我们现在将介绍三种类型的分组符号。
\[\begin{array}{lc} \text{Parentheses} & \mathrm{()} \\ \text{Brackets} & \mathrm{[]} \\ \text{Braces} & \mathrm{ \{ \} } \end{array}\]
以下是一些包含分组符号的表达式示例。 在本节后面,我们将简化这样的表达式。
\[8(14−8) \qquad 21−3[2+4(9−8)] \qquad 24÷ \{13−2[1(6−5)+4]\}\]
在英语中,短语和句子有什么区别? 一个短语表示一个本身并不完整的单一想法,但一个句子代表一个完整的陈述。 句子有主语和动词。 在代数中,我们有表达式和方程。
表达式是数字、变量或使用运算符号的数字和变量的组合。
\[\begin{array}{lll} \textbf{Expression} & \textbf{Words} & \textbf{English Phrase} \\ \mathrm{3+5} & \text{3 plus 5} & \text{the sum of three and five} \\ \mathrm{n−1} & n\text{ minus one} & \text{the difference of } n \text{ and one} \\ \mathrm{6·7} & \text{6 times 7} & \text{the product of six and seven} \\ \frac{x}{y} & x \text{ divided by }y & \text{the quotient of }x \text{ and }y \end{array} \]
请注意,英语短语不构成完整的句子,因为该短语没有动词。
方程是由等号连接的两个表达式。 当你读取方程中符号所代表的单词时,你就有了完整的英语句子。 等号表示动词。
方程是两个由等号连接的表达式。
\[\begin{array}{ll} \textbf{Equation} & \textbf{English Sentence} \\ 3+5=8 & \text{The sum of three and five is equal to eight.} \\ n−1=14 & n \text{ minus one equals fourteen.} \\ 6·7=42 & \text{The product of six and seven is equal to forty-two.} \\ x=53 & x \text{ is equal to fifty-three.} \\ y+9=2y−3 & y \text{ plus nine is equal to two } y \text{ minus three.} \end{array}\]
假设我们需要将 2 乘以九倍。 我们可以把它写成\(2·2·2·2·2·2·2·2·2\)。 这很乏味,可能很难追踪所有这些 2 秒,所以我们使用指数。 我们\(2·2·2\)按原样写\(\mathrm{2^3}\)\(2·2·2·2·2·2·2·2·2\)作\(2^9\)。 在诸如这样的表达式中\(2^3\),2 被称为基数,3 被称为指数。 指数告诉我们需要多少次才能将基数相乘。

我们说\(2^3\)的是指数表示法,\(2·2·2\)是扩展表示法。
\(a^n\)表示该数字的乘以\(n\)因子\(a\)。
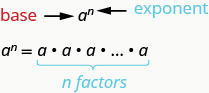
表达式\(a^n\)被解读\(a\)为权\(n^{th}\)力。
当我们阅读\(a^n\) “\(n^{th}\)力量” 时,我们通常会读\(“a\)到:
\[\begin{array}{cc} a^2 & “a \text{ squared}” \\ a^3 & “a \text{ cubed}” \end{array}\]
我们稍后再看看原因,\(a^2\)并\(a^3\)有特殊的名字。
该@@ 表显示了我们如何读取一些带有指数的表达式。
| 表情 | 用言语表达 | |
|---|---|---|
| 7 2 | 7 到第二个幂或 | 7 平方 |
| 5 3 | 5 到第三次幂或 | 5 立方体 |
| 9 4 | 9 到第四次方 | |
| 12 5 | 12 到第五次力量 |
使用运算顺序简化表达式
简化表达式意味着尽一切可能进行数学运算。 例如,为了简化起见,\(\mathrm{4·2+1}\)我们首先乘\(\mathrm{4⋅2}\)以得到 8,然后将 1 相加得到 9。 养成的一个好习惯是沿着页面向下移动,将过程的每个步骤写在上一个步骤的下方。 刚才描述的例子看起来像这样:
\[ 4⋅2+1 \\ 8+1 \\ 9\]
通过在简化表达式时不使用等号,可以避免将表达式与方程混淆。
要简化表达式,请在表达式中执行所有操作。
我们已经介绍了代数中使用的大多数符号和符号,但现在我们需要澄清运算顺序。 否则,表达式可能具有不同的含义,并且可能产生不同的值。
例如,以表达式为例\(4+3⋅7\)。 有些学生通过将该结果加起来\(4+3\)然后乘以 7 来简化得到 49 的过程。 其他人得到 25,\(3·7\)先乘以 4 再相加。
相同的表达式应该给出相同的结果。 因此,数学家制定了一些称为运算顺序的指导方针。
- 圆括号和其他分组符号
- 简化括号或其他分组符号内的所有表达式,首先处理最内侧的括号。
- 指数
- 使用指数简化所有表达式。
- 乘法和除法
- 按从左到右的顺序执行所有乘法和除法。 这些操作具有同等的优先级。
- 加法和减法
- 按从左到右的顺序执行所有加法和减法。 这些操作具有同等的优先级。
学生经常问:“我怎么能记住这个订单?” 这里有一种方法可以帮助你记住:取每个关键词的第一个字母,然后用愚蠢的短语 “请原谅我亲爱的莎莉姨妈” 代替。
\[\begin{array}{ll} \text{Parentheses} & \text{Please} \\ \text{Exponents} & \text{Excuse} \\ \text{Multiplication Division} & \text{My Dear} \\ \text{Addition Subtraction} & \text{Aunt Sally} \end{array}\]
将 “M y D ear” 结合在一起真是太好了,因为这提醒我们,我的乘法和 d d ivision 具有同等的优先级。 我们不总是在除法之前进行乘法,也不总是在乘法之前进行除法。 我们按从左到右的顺序排列。
同样,“A unt S ally” 结合在一起,因此提醒我们,加法和减法也有同等的优先级,我们按从左到右的顺序进行。
简化:\(18÷6+4(5−2)\)。
- 回答
-
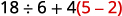
圆括号? 是的,先减去。 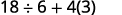
指数? 不。 乘法还是除法? 是的。 先除以是因为我们从左到右乘以和除法。 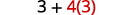
还有其他乘法或除法吗? 是的。 乘以。 
还有其他除法乘法吗? 不。 有加法或减法吗? 是的。 添加。 
简化:\(30÷5+10(3−2).\)
- 回答
-
16
简化:\(70÷10+4(6−2).\)
- 回答
-
23
当有多个分组符号时,我们首先简化最内侧的括号,然后向外移动。
简化:\(5+2^3+3[6−3(4−2)].\)
- 回答
-
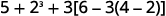
有没有圆括号(或其他分组符号)? 是的。 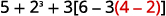
将注意力集中在方括号内的圆括号上。 减去。 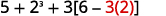
继续在方括号内乘以。 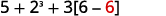
继续在方括号内减去。 
方括号内的表达式无需进一步简化。 有指数吗? 是的。 简化指数。 
有乘法或除法吗? 是的。 乘以。 
减法有加法吗? 是的。 添加。 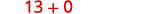
添加。 
简化:\(9+5^3−[4(9+3)].\)
- 回答
-
86
简化:\(7^2−2[4(5+1)].\)
- 回答
-
1
计算表达式
在最后几个示例中,我们使用运算顺序简化了表达式。 现在,我们将再次按照运算顺序计算一些表达式。 计算表达式意味着在变量被给定数字替换时找到表达式的值。
计算表达式意味着在变量被给定数字替换时找到表达式的值。
要计算表达式,请用该数字代替表达式中的变量,然后简化表达式。
评估时间\(x=4\):a.\(x^2\) b.\(3^x\) c\(2x^2+3x+8\).
- 回答
-
一个。
b。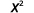
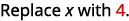

使用指数的定义。 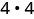
简化。 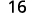
c。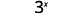
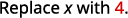

使用指数的定义。 
简化。 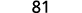
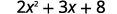
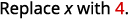
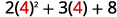
遵循操作顺序。 .jpg)
评估时间\(x=3\),a.\(x^2\) b.\(4^x\) c\(3x^2+4x+1\).
- 回答
-
a. 9
b. 64
c. 40
评估时间\(x=6\),a.\(x^3\) b.\(2^x\) c\(6x^2−4x−7\).
- 回答
-
a. 216
b. 64
c. 185
识别并合并相似的术语
代数表达式由术语组成。 项是一个常数,或者是一个常量与一个或多个变量的乘积。
项是一个常量或一个常量与一个或多个变量的乘积。
术语的示例是\(7,\,y,\,5x^2,\,9a,\)和\(b^5\)。
与变量相乘的常数称为系数。
项的系数是将项中的变量相乘的常数。
将系数视为变量前面的数字。 该项的系数\(3x\)为 3。 当我们写的时候\(x\),系数为 1,因为\(x=1⋅x\)。
有些术语具有共同的特征。 当两个项是常量或具有相同的变量和指数时,我们说它们就像项一样。
看看以下 6 个术语。 哪些似乎有共同的特征?
\[5x \quad 7 \quad n^2 \quad 4 \quad 3x \quad 9n^2\]
我们说,
\(7\)就像术语一样。\(4\)
\(5x\)就像术语一样。\(3x\)
\(n^2\)就像术语一样。\(9n^2\)
要么是常量,要么将相同变量提高到相同幂的项被称为类似项。
如果表达式中有相似的术语,则可以通过组合相似的术语来简化表达式。 我们添加系数并保持相同的变量。
\[\begin{array}{lc} \text{Simplify.} & 4x+7x+x \\ \text{Add the coefficients.} & 12x \end{array}\]
简化:\(2x^2+3x+7+x^2+4x+5\)。
- 回答
-



简化:\(3x^2+7x+9+7x^2+9x+8\)。
- 回答
-
\(10x^2+16x+17\)
简化:\(4y^2+5y+2+8y^2+4y+5.\)
- 回答
-
\(12y^2+9y+7\)
- 识别相似的术语。
- 重新排列表达式,就像术语组合在一起一样。
- 将系数相加或减去,并为每组相似项保留相同的变量。
将英语短语翻译成代数表达式
我们列出了代数中使用的许多运算符号。 现在,我们将使用它们将英语短语翻译成代数表达式。 我们所讨论的符号和变量将帮助我们做到这一点。 表中总结了它们。
| 操作 | 短语 | 表情 |
|---|---|---|
| 加法 | \(a\)再加上\(b\)
\(a\)和@@ 的总和\(b\) \(a\)增加了\(b\) \(b\)超过\(a\) \(a\)和@@ 的总和\(b\) \(b\)已添加到\(a\) |
\(a+b\) |
| 减法 | \(a\)减去\(b\)
\(a\)和的区别\(b\) \(a\)减少了\(b\) \(b\)小于\(a\) \(b\)从中减去\(a\) |
\(a−b\) |
| 乘法 | \(a\)倍\(b\)
\(a\)和@@ 的乘积\(b\) 两次\(a\) |
\(a·b,\,ab,\,a(b),\,(a)(b)\)
\(2a\) |
| 部门 | \(a\)除以\(b\)
\(a\)和的商\(b\) \(a\)和的比率\(b\) \(b\)分为\(a\) |
\(a÷b,\,a/b,\,\frac{a}{b},\,b \overline{\smash{)}a}\) |
使用四个操作仔细查看这些短语:

每个短语都告诉我们对两个数字进行运算。 查找 and 的单词并找到数字。
每个短语都告诉我们对两个数字进行运算。 查找 and 的单词并找到数字。
将每个英语短语翻译成代数表达式:
a.\(14x\) 和的区别\(9\)
b.\(8y^2\) 和的商\(3\)c. 比十二多\(y\)
d. 少于七个\(49x^2\)
将英语短语翻译成代数表达式:
a.\(14x^2\) 和的区别\(13\)
b.\(12x\) 和的商\(2\)
c. 超\(13\)过\(z\)
d.\(18\) 小于\(8x\)
- 回答
-
a.\(14x^2−13\) b。\(12x÷2\)
c.\(z+13\) d。\(8x−18\)
将英语短语翻译成代数表达式:
a.\(17y^2\) 和的总和\(19\)
b.\(7\) 和的产物\(y\)
c. 比十一个多\(x\)
d. 少于十四个\(11a\)
- 回答
-
a.\(17y^2+19\) b。\(7y\)
c.\(x+11\) d。\(11a−14\)
我们会仔细研究这些词语,以帮助我们区分乘总和和和和和与乘积。
将英语短语翻译成代数表达式:
a. 和之\(x\)和的八倍\(y\)
b. 八次之\(x\)和和\(y\)
- 回答
-
有两个运算词 —— 时间告诉我们乘以,总和告诉我们相加。
a. 因为我们要\(8\)乘以总和,所以我们需要在和、两边加上圆括\(y\)号\((x+y)\)。\(x\) 这迫使我们首先确定总和。 (记住操作顺序。)
\[\text{eight times the sum of }x \text{ and }y \\ 8(x+y)\]
b. 总而言之,我们要查看 and 和 and 的单词,看看添加了什么。 这里我们取八倍的总\(x\)和\(y\)。
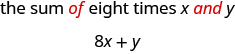
将英语短语翻译成代数表达式:
a. 和之\(p\)和的四倍\(q\)
b. 四次之\(p\)和和\(q\)
- 回答
-
a.\(4(p+q)\) b。\(4p+q\)
将英语短语翻译成代数表达式:
a. 两次之差\(x\)和\(8\)
b.\(x\) 和之差的两倍\(8\)
- 回答
-
a.\(2x−8\) b。\(2(x−8)\)
在本课程的后面部分,我们将运用我们的代数技能来求解应用程序。 第一步将是将英语短语翻译成代数表达式。 我们将在接下来的两个示例中看到如何执行此操作。
矩形的长度比宽度小 14。 让我们来\(w\)表示矩形的宽度。 为矩形的长度写一个表达式。
- 回答
-
\[\begin{array}{lc} \text{Write a phrase about the length of the rectangle.} & \text{14 less than the width} \\ \text{Substitute }w \text{ for “the width.”} & w \\ \text{Rewrite less than as subtracted from.} & \text{14 subtracted from } w \\ \text{Translate the phrase into algebra.} & w−14 \end{array}\]
矩形的长度比宽度小 7。 让我们来\(w\)表示矩形的宽度。 为矩形的长度写一个表达式。
- 回答
-
\(w−7\)
矩形的宽度\(6\)小于长度。 让我们来\(l\)表示矩形的长度。 为矩形的宽度写一个表达式。
- 回答
-
\(l−6\)
下一个示例中的表达式将用于我们很快就会看到的典型硬币混合问题。
June 的钱包里有硬币和四分之一。 硬币的数量是七分钱,少于季度数的四倍。 让我们来\(q\)表示季度数。 为硬币数写一个表达式。
- 回答
-
\[\begin{array}{lc} \text{Write a phrase about the number of dimes.} & \text{7 less than 4 times }q \\ \text{Translate 4 times }q. & \text{7 less than 4}q \\ \text{Translate the phrase into algebra.} & 4q−7 \end{array}\]
杰弗里口袋里有一角钱和四分之一。 硬币的数量比季度数少四倍的八分钱。 让我们来\(q\)表示季度数。 为硬币数写一个表达式。
- 回答
-
\(4q−8\)
Lauren 的钱包里有硬币和镍。 硬币的数量是镍数量的三倍多七倍。 让我们来\(n\)表示镍的数量。 为硬币数写一个表达式。
- 回答
-
\(7n+3\)
关键概念
- 可@@ 分性测试
如果最后一位数字为 0、
2、4、6 或 8,则数字可被:2 整除。
如果数字之和可被 3 整除,则为 3。
如果最后一位数字为 5 或 0,则为 5。
如果它可以被 2 和 3 整除,则为 6。
如果以 0 结尾,则为 10。 - 如何找到复合数的素数分解。
- 找出乘积为给定数字的两个因子,然后使用这些数字创建两个分支。
- 如果一个因子是素数,则该分支是完整的。 环绕素数,就像树上的花蕾一样。
- 如果一个因子不是素数,则将其写成两个因子的乘积并继续该过程。
- 将复合数写成所有圈出素数的乘积。
- 如何使用素数法找到最小公倍数。
- 将每个数字写成素数的乘积。
- 列出每个数字的素数。 尽可能垂直匹配素数。
- 把柱子放下。
- 将因子相乘。
- 等式
\(a=b\)符号读作 “等\(a\)于”\(b\)。 符号 “=” 被称为等号。 
- 不等式符号
不等式符号 单词 \(a≠b\) \(a\)不等于\(b\)。 \(a<b\) \(a\)小于\(b\)。 \(a≤b\) \(a\)小于或等于\(b\)。 \(a>b\) \(a\)大于\(b\)。 \(a≥b\) \(a\)大于或等于\(b\)。 - 分组符号\(\begin{array}{lc} \text{Parentheses} & \mathrm{()} \\ \text{Brackets} & \mathrm{[]} \\ \text{Braces} & \mathrm{ \{ \} } \end{array}\)
- 指数\(a^n\)表示法本身乘以\(a\)乘以,\(n\)乘以。 表达式 an 被读取\(a\)为次\(n^{th}\)方。
- 简化表达式
要简化表达式,请在表达式中执行所有操作。 - 如何使用操作顺序。
- 圆括号和其他分组符号
- 简化括号或其他分组符号内的所有表达式,首先处理最内侧的括号。
- 指数
- 使用指数简化所有表达式。
- 乘法和除法
- 按从左到右的顺序执行所有乘法和除法。 这些操作具有同等的优先级。
- 加法和减法
- 按从左到右的顺序执行所有加法和减法。 这些操作具有同等的优先级。
- 圆括号和其他分组符号
- 如何合并相似的术语。
- 识别相似的术语。
- 重新排列表达式,就像术语组合在一起一样。
- 将系数相加或减去,并为每组相似项保留相同的变量。
操作 短语 表情 加法 \(a\)加\(b\)
上\(a\)和的总和\(b\)
\(a\)\(b\)
\(b\)增加大于\(a\)
和相\(b\)
\(b\)加的总\(a\)和\(a\)\(a+b\) 减法 \(a\)减去\(b\)
之差\(a\),\(b\)
\(a\)减\(b\)
\(b\)小于\(a\)
\(b\)从中减去\(a\)\(a−b\) 乘法 \(a\)乘\(b\)
以的乘积\(a\)和\(b\)
两次\(a\)\(a·b,\,ab,\,a(b),\,(a)(b)\)
\(2a\)
部门 \(a\)除以 \(b\)
\(a\)和的商 \(b\)
\(a\)和的比率 \(b\)
\(b\)分为\(a\)\(a÷b,\,a/b,\,\frac{a}{b},\,b \overline{\smash{)}a}\)
词汇表
- 系数
- 项的系数是将项中的变量相乘的常数。
- 复合数字
- 复合数是非素数的计数数。 除了 1 和数字本身外,它还有其他因子。
- 不变
- 常量是一个其值始终保持不变的数字。
- 可被数字整除
- 如果一个数字\(m\)是的倍数 \(n\),\(m\)则可被整除\(n\)。
- 方程
- 方程是两个由等号连接的表达式。
- 计算表达式
- 计算表达式意味着在变量被给定数字替换时找到表达式的值。
- 表情
- 表达式是数字、变量或使用运算符号的数字和变量的组合。
- 因素
- 如果\(a·b=m\)、那么\(a\)和\(b\)是因子\(m\)。
- 最小公倍数
- 两个数字的最小公倍数 (LCM) 是两个数字的倍数的最小数字。
- 像术语一样
- 要么是常量,要么将相同变量提高到相同幂的项被称为类似项。
- 数字的倍数
- \(n\)如果数字是计数数字的乘积,则数字是的倍数\(n\)。
- 操作顺序
- 运算顺序是简化表达式的既定指导方针。
- 素数分解
- 数字的素数分解是等于该数字的质数的乘积。
- 素数
- 质数是大于 1 的计数数,其唯一因子为 1 和数字本身。
- 简化表达式
- 简化表达式意味着尽一切可能进行数学运算。
- 术语
- 项是一个常数,或者是一个常量与一个或多个变量的乘积。
- 变量
- 变量是一个字母,它代表一个数值,该数字的值可能会改变。