10.4: الاضمحلال الإشعاعي

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• وصف تحلل مادة مشعة من حيث ثابت الاضمحلال ونصف العمر
• استخدم قانون التحلل الإشعاعي لتقدير عمر المادة
• اشرح العمليات الطبيعية التي تسمح بتأريخ الأنسجة الحية باستخدام ¹⁴ C

في عام 1896، اكتشف أنطوان بيكريل أن الصخور الغنية باليورانيوم تنبعث منها أشعة غير مرئية يمكنها تعتيم لوحة فوتوغرافية في حاوية مغلقة. يقدم العلماء ثلاث حجج حول الأصل النووي لهذه الأشعة. أولاً، لا تختلف تأثيرات الإشعاع باختلاف الحالة الكيميائية؛ أي ما إذا كانت المادة المنبعثة في شكل عنصر أو مركب. ثانيًا، لا يختلف الإشعاع مع التغيرات في درجة الحرارة أو الضغط - كلا العاملين يمكن أن يؤثرا بدرجة كافية على الإلكترونات في الذرة. ثالثًا، لا تتوافق الطاقة الكبيرة جدًا للأشعة غير المرئية (حتى مئات المركبات الكهربائية) مع انتقالات الإلكترون الذري (فقط عدد قليل من eV). اليوم، يتم تفسير هذا الإشعاع من خلال تحويل الكتلة إلى طاقة في أعماق نواة الذرة. يُطلق على الانبعاث التلقائي للإشعاع من النوى اسم النشاط الإشعاعي النووي (الشكل$\PageIndex{1}$).

الشكل$\PageIndex{1}$: رمز الإشعاع المؤين الدولي معروف عالميًا كرمز تحذير للإشعاع النووي.

قانون الاضمحلال الإشعاعي

عندما تتحول نواة فردية إلى أخرى مع انبعاث الإشعاع، يُقال إن النواة تتحلل. يحدث التحلل الإشعاعي لجميع النوى مع$Z > 82$، وكذلك لبعض النظائر غير المستقرة مع$Z < 83$. يتناسب معدل الانحلال مع عدد النوى الأصلية (غير المتحللة) N في المادة. يتم كتابة عدد النوى المفقودة بسبب التحلل،$-dN$ في الفاصل الزمني dt

$$-\dfrac{dN}{dt} = \lambda N \label{eq2}$$

حيث$\lambda$ يسمى ثابت الاضمحلال. (تشير علامة الطرح إلى انخفاض عدد النوى الأصلية بمرور الوقت.) وبعبارة أخرى، كلما زاد عدد النوى المتاحة للتحلل، زاد عدد النوى التي تتحلل (بالوقت dt). يمكن إعادة كتابة المعادلة\ ref {eq2} كـ

$$\dfrac{dN}{N} = -\lambda dt. \nonumber$$

نحصل على دمج طرفي المعادلة، وتحديد$N_0$ عدد النوى الموجودة$t = 0$

$$\int_{N_0}^N \dfrac{dN'}{N} = - \int_0^t \lambda dt'. \nonumber$$

هذا يعطينا

$$\ln\dfrac{N}{N_0} = -\lambda t. \label{eq4}$$

بأخذ الجانبين الأيسر والأيمن من المعادلة\ ref {eq4} كقوة$e$، لدينا قانون التحلل الإشعاعي.

قانون الاضمحلال الإشعاعي

إجمالي$N$ عدد النوى المشعة المتبقية بعد الوقت$t$ هو

$$N = N_0e^{-\lambda t} \label{decay law}$$

$\lambda$أين ثابت الاضمحلال للنواة المعينة.

ينخفض العدد الإجمالي للنواة بسرعة كبيرة في البداية، ثم ببطء أكثر (الشكل$\PageIndex{2}$).

الشكل$\PageIndex{2}$: يوضح مخطط قانون الاضمحلال الإشعاعي أن عدد النوى المتبقية في عينة الاضمحلال ينخفض بشكل كبير خلال اللحظات الأولى من الاضمحلال.

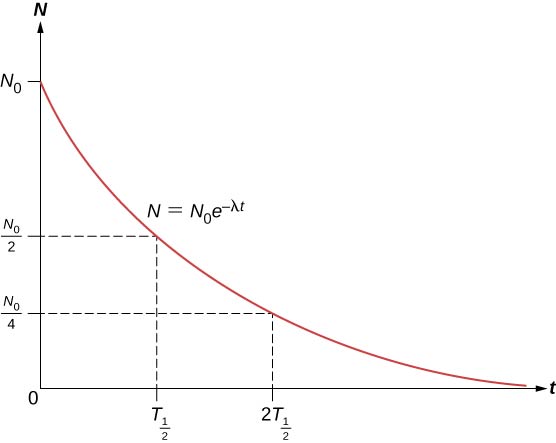
يُعرّف نصف$(T_{1/2})$ عمر المادة المشعة بأنه الوقت الذي يتحلل فيه نصف النوى الأصلية (أو الوقت الذي يبقى فيه نصف النوى الأصلية). تظهر فترات نصف عمر النظائر غير المستقرة في مخطط النويدات. وبالتالي فإن عدد النوى المشعة المتبقية بعد عدد صحيح (n) من فترات نصف العمر هو

$$N = \dfrac{N_0}{2^n} \label{eq5}$$

إذا كان ثابت$(\lambda)$ الاضمحلال كبيرًا، يكون عمر النصف صغيرًا والعكس صحيح. لتحديد العلاقة بين هذه الكميات، لاحظ أنه متى$t = T_{1/2}$، إذن$N = N_0/2$.

وبالتالي، يمكن إعادة كتابة المعادلة\ ref {eq5} كـ

$$\dfrac{N_0}{2} = N_0e^{-\lambda T_{1/2}}. \nonumber$$

ينتج عن تقسيم كلا الجانبين$N_0$ وأخذ اللوغاريتم الطبيعي

$$\ln \dfrac{1}{2} = \ln \, e^{-\lambda T_{1/2}} \nonumber$$

مما يقلل إلى

$$\lambda = \dfrac{0.693}{T_{1/2}}. \nonumber$$

وبالتالي، إذا عرفنا عمر النصف T _1/2 لمادة مشعة، فيمكننا أن نجد ثابت تحللها. يُعرَّف $\overline{T}$عمر المادة المشعة بأنه متوسط مقدار الوقت الذي توجد فيه النواة قبل التحلل. إن عمر المادة هو مجرد مقلوب ثابت الاضمحلال، المكتوب على النحو التالي

$$\overline{T} = \dfrac{1}{\lambda}. \nonumber$$

يتم تعريف النشاط A على أنه حجم معدل الانحلال، أو

$$A = -\dfrac{dN}{dt} = \lambda N = \lambda N_0 e^{-\lambda t}. \nonumber$$

يكون التغيير المتناهي الصغر dN في الفاصل الزمني dt سالبًا لأن عدد الجسيمات الأصلية (غير المتحللة) يتناقص، وبالتالي فإن النشاط (A) إيجابي. تعريف النشاط الأولي$A_0 = \lambda N_0$ كما يلي:

$$A = A_0 e^{-\lambda t}. \label{eq8}$$

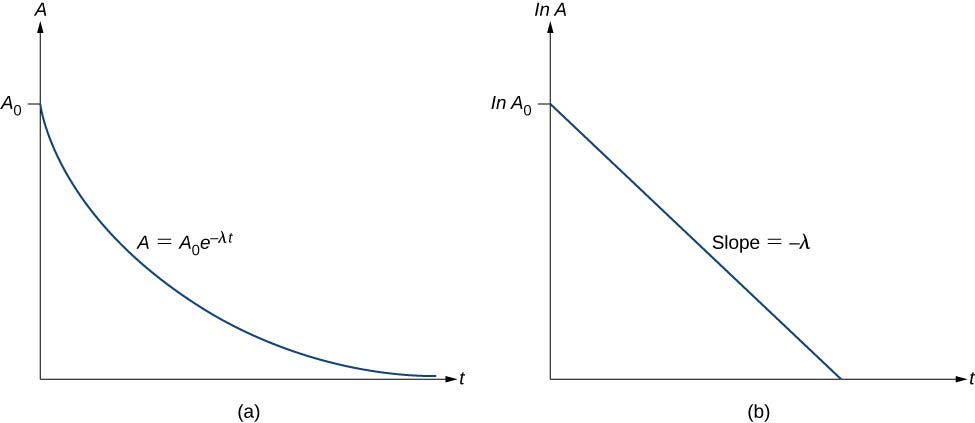
وبالتالي، يتناقص النشاط A للمادة المشعة بشكل كبير مع مرور الوقت (الشكل$\PageIndex{3}$).

الشكل$\PageIndex{3}$: (أ) مخطط للنشاط كدالة للوقت (ب) إذا قمنا بقياس النشاط في أوقات مختلفة، فيمكننا رسم\ ln A مقابل t، والحصول على خط مستقيم.

مثال$\PageIndex{1}$: Decay Constant and Activity of Strontium-90

يبلغ نصف عمر السترونتيوم 90 28.8 y$\ce{_{38}^{90}Sr}$، أوجد (أ) ثابت تحلله و (ب) النشاط الأولي البالغ 1.00 g من المادة.

إستراتيجية

يمكننا العثور على ثابت الاضمحلال مباشرة من المعادلة\ ref {eq8}. لتحديد النشاط، نحتاج أولاً إلى إيجاد عدد النوى الموجودة.

الحل

أ- وجد أن ثابت الاضمحلال هو

$$\lambda = \dfrac{0.693}{T_{1/2}} = \left(\dfrac{0.693}{T_{1/2}}\right)\left(\dfrac{1 \, yr}{3.16 \times 10^7 \, s}\right) = 7.61 \times 10^{-10} \, s^{-1}. \nonumber$$

ب- الكتلة الذرية$_{38}^{90}Sr$ تساوي 89.91 غرامًا، وباستخدام عدد$N_A = 6.022 \times 10^{23}$ ذرات/مول من Avogadro، نجد العدد الأولي للنواة في 1.00 g من المادة:

$$N_0 = \dfrac{1.00 \, g}{89.91 \, g} (N_A) = 6.70 \times 10^{21} \, nuclei. \nonumber$$

من هذا نجد أن النشاط$A_0$ عند$t = 0$ 1.00 g من السترونتيوم 90 هو

$$A_0 = \lambda N_0 = (7.61 \times 10^{-10} s^{-1})(6.70 \times 10^{21} \, nuclei) = 5.10 \times 10^{12} \, decays/s. \nonumber$$

بالتعبير عن$\lambda$ عمر النصف للمادة، نحصل على

$$A = A_0 e^{-(0.693/T_{1/2})T_{1/2}} = A_0 e^{-0.693} = A_0/2. \label{eq11}$$

لذلك، ينخفض النشاط إلى النصف بعد نصف عمر واحد. يمكننا تحديد ثابت الاضمحلال$\lambda$ من خلال قياس النشاط كدالة للوقت. بأخذ اللوغاريتم الطبيعي للجانبين الأيسر والأيمن من المعادلة\ ref {eq11}، نحصل على

$$\ln \, A = - \lambda t + \ln \, A_0. \nonumber$$

تتبع هذه المعادلة الشكل الخطي$y = mx + b$. إذا قمنا برسم\ ln A مقابل t، فإننا نتوقع خطًا مستقيمًا بمنحدر$-\lambda$ ونقطة تقاطع y$\ln \, A_0$ (الشكل$\PageIndex{3b}$). يتم التعبير عن النشاط A بوحدات البيكريل (Bq)، حيث توجد وحدة واحدة$1 \, Bq = 1 \, decay \, per \, second$. يمكن أيضًا التعبير عن هذه الكمية بالتحلل في الدقيقة أو الاضمحلال سنويًا. تعتبر وحدة الكوري (Ci) واحدة من أكثر وحدات النشاط شيوعًا، وتُعرف بأنها نشاط 1 g من$^{226}Ra$. العلاقة بين Bq و Ci هي

$$1 \, Ci = 3.70 \times 10^{10}Bq. \nonumber$$

مثال$\PageIndex{2}$: What is$^{14}C$ Activity in Living Tissue?

الكربون تقريبًا$20\%$ من جسم الإنسان من حيث الكتلة. احسب النشاط الناتج$^{14}C$ في 1.00 kg من الكربون الموجود في كائن حي. عبّر عن النشاط بوحدات Bq و Ci.

إستراتيجية

$^{14}C$يُحدَّد النشاط باستخدام المعادلة$A_0 = \lambda N_0$، حيث هو ثابت الاضمحلال$N_0$ وهو عدد الأنوية المشعة. يتم تحديد عدد$^{14}C$ النوى في عينة وزنها 1.00 كجم في خطوتين. أولاً، نحدد عدد$^{12}C$ النوى باستخدام مفهوم المول. ثانيًا، نضرب هذه القيمة في$1.3 \times 10^{-12}$ (الوفرة المعروفة$^{14}C$ في عينة الكربون من كائن حي) لتحديد عدد$^{14}C$ النوى في الكائن الحي. يتم تحديد ثابت الاضمحلال من عمر النصف المعروف لـ$^{14}C$ (متاح من [رابط]).

الحل

تبلغ كتلة مول واحد من الكربون 12.0 g، نظرًا لأنه نقي تقريبًا$^{12}C$. وبالتالي، فإن عدد نوى الكربون في الكيلوغرام هو

$$N(^{12}C) = \dfrac{6.02 \times 10^{23} mol^{-1}}{12.0 \, g/mol} \times (1000 \, g) = 5.02 \times 10^{25}. \nonumber$$

وبالتالي فإن عدد$^{14}C$ النوى في 1 كجم من الكربون هو

$$N(^{14}C) = (5.02 \times 10^{25})(1.3 \times 10^{_12}) = 6.52 \times 10^{13}. \nonumber$$

الآن يمكننا العثور على النشاط$A$ باستخدام Equation\ ref {eq11}. يمنحنا إدخال القيم المعروفة

$$A = \dfrac{0.693 (6.52 \times 10^{13})}{5730 \, y} = 7.89 \times 10^9 \, y^{-1} \nonumber$$

أو$7.89 \times 10^9$ تتحلل في السنة. لتحويل هذا إلى الوحدة Bq، نقوم ببساطة بتحويل السنوات إلى ثوانٍ. وهكذا،

$$A = (7.89 \times 10^9 \, y^{-1}) \dfrac{1.00 \, y}{3.16 \times 10^7 \, s} = 250 \, Bq, \nonumber$$

أو 250 اضمحلال في الثانية. للتعبير عن A في curies، نستخدم تعريف كوري،

$$A = \dfrac{250 \, Bq}{3.7 \times 10^{10} \, Bq/Ci} = 6.76 \times 10^{-9} Ci. \nonumber$$

وهكذا،

$$A = 6.76 \, nCi. \nonumber$$

الأهمية

ما يقرب$20\%$ من جسم الإنسان من حيث الوزن هو الكربون. تحدث مئات$^{14}C$ الاضمحلال في جسم الإنسان كل ثانية. يشكل الكربون 14 والمواد المشعة الأخرى التي تحدث بشكل طبيعي في الجسم التعرض الخلفي للشخص للإشعاع النووي. كما سنرى لاحقًا في هذا الفصل، فإن مستوى النشاط هذا أقل بكثير من الجرعات القصوى الموصى بها.

المواعدة المشعة

التأريخ الإشعاعي هو تقنية تستخدم النشاط الإشعاعي الطبيعي لتحديد عمر المادة, مثل صخرة أو قطعة أثرية قديمة. تتمثل الطريقة الأساسية في تقدير العدد الأصلي للنواة في المادة والعدد الحالي للنواة في المادة (بعد الاضمحلال), ثم استخدم القيمة المعروفة لثابت الاضمحلال$\lambda$ والمعادلة\ ref {قانون الاضمحلال} لحساب الوقت الإجمالي للانحلال,$t$.

طريقة مهمة للتأريخ الإشعاعي هي التأريخ بالكربون 14. يتم إنتاج نوى الكربون 14 عندما يصطدم الإشعاع الشمسي عالي الطاقة$^{14}N$ بالنواة في الغلاف الجوي العلوي ويتحلل لاحقًا بعمر نصف يبلغ 5730 عامًا. يحتوي الكربون المشع على نفس كيمياء الكربون المستقر، لذلك فهو يتحد مع الغلاف البيئي ويصبح في النهاية جزءًا من كل كائن حي. يحتوي الكربون 14 على وفرة قدرها 1.3 جزء لكل تريليون من الكربون العادي. لذلك، إذا كنت تعرف عدد نوى الكربون في جسم ما، فإنك تضرب هذا الرقم في$1.3 \times 10^{-12}$ إيجاد عدد$^{14}C$ النوى في ذلك الكائن. عندما يموت كائن حي، يتوقف تبادل الكربون مع البيئة، ولا$^{14}C$ يتم تجديده أثناء تحلله.

من$^{14}C$ خلال مقارنة وفرة القطع الأثرية، مثل أغلفة المومياء، بالوفرة الطبيعية في الأنسجة الحية، يمكن تحديد عمر المومياء (أو الوقت منذ وفاة الشخص). يمكن استخدام التأريخ بالكربون 14 للأنسجة البيولوجية التي يصل عمرها إلى 50,000 عام، ولكنه بشكل عام أكثر دقة للعينات الأصغر سنًا، نظرًا لأن وفرة$^{14}C$ النوى فيها أكبر. لا تحتوي المواد البيولوجية القديمة جدًا$^{14}C$ على الإطلاق. يمكن التحقق من صحة التأريخ بالكربون بوسائل أخرى, مثل المعرفة التاريخية أو عن طريق عد حلقات الأشجار.

كهف الدفن القديم

في كهف الدفن القديم، يكتشف فريقك من علماء الآثار أثاثًا خشبيًا قديمًا. فقط$80\%$ من$^{14}C$ البقايا الأصلية في الخشب. كم عمر الأثاث؟

إستراتيجية

بيان المشكلة يعني ذلك$N/N_0 = 0.80$. لذلك، نعيد ترتيب المعادلة\ ref {decay law} للعثور على المنتج،$\lambda t$. نحن نعلم أن عمر النصف$^{14}C$ هو 5730 y، لذلك نعرف أيضًا ثابت الاضمحلال، وبالتالي وقت الانحلال الكلي$t$.

الحل

نعيد ترتيب المعادلة\ المرجع {قانون الاضمحلال}$N/N_0$ لإعطاء

$$\dfrac{N}{N_0} = e^{-\lambda t}. \nonumber$$

وهكذا

$$0.80 = e^{-\lambda t}. \nonumber$$

ينتج عن أخذ اللوغاريتم الطبيعي لكلا الجانبين

$$\ln \, 0.80 = - \lambda t,\nonumber$$

بحيث

$$-0.223 = -\lambda t. \nonumber$$

$t$تمنحنا إعادة ترتيب المعادلة للعزل

$$t = \dfrac{0.223}{\left(\dfrac{0.693}{5730 \, y}\right)} = 1844 \, y. \nonumber$$

الأهمية

يبلغ عمر الأثاث 2000 عام تقريبًا - وهو اكتشاف مثير للإعجاب. تدور حالة عدم اليقين النموذجية بشأن التأريخ بالكربون 14$5\%$، لذا فإن عمر الأثاث يتراوح بين 1750 و 1950 عامًا. يجب تأكيد هذا النطاق الزمني بأدلة أخرى، مثل السجلات التاريخية.

التمارين$\PageIndex{3}$

تحتوي النويدات المشعة على معدل تحلل مرتفع. ماذا يعني هذا بالنسبة لنصف عمرها ونشاطها؟

إجابة

يرتبط نصف العمر ارتباطًا عكسيًا بمعدل الانحلال، لذا فإن عمر النصف قصير. يعتمد النشاط على كل من عدد الجسيمات المتحللة ومعدل التحلل، لذلك يمكن أن يكون النشاط كبيرًا أو صغيرًا.

قم بزيارة لعبة المواعدة المشعة للتعرف على أنواع التأريخ الإشعاعي وجرب يدك في تحديد تاريخ بعض الأشياء القديمة.