10.3: طاقة الربط النووي

Last updated
Save as PDF

Page ID: 196744

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

احسب العيب الكتلي وطاقة الربط لمجموعة واسعة من النوى
استخدم رسمًا بيانيًا لطاقة الربط لكل نواة (BEN) مقابل رسم بياني لرقم الكتلة (A) لتقييم الاستقرار النسبي للنواة
قارن طاقة ربط النيوكليون في النواة بالطاقة المؤينة للإلكترون في الذرة

القوى التي تربط النيوكليونات معًا في نواة ذرية أكبر بكثير من تلك التي تربط الإلكترون بالذرة من خلال الجذب الكهروستاتيكي. ويتجلى ذلك من خلال الأحجام النسبية للنواة الذرية والذرة (\(10^{-15}\)و\(10^{-10}\) m، على التوالي). وبالتالي فإن الطاقة المطلوبة لاستخراج النيوكليون من النواة أكبر بكثير من تلك المطلوبة لإزالة (أو تأين) إلكترون في الذرة. بشكل عام، تتضمن جميع التغييرات النووية كميات كبيرة من الطاقة لكل جسيم يخضع للتفاعل. هذا له العديد من التطبيقات العملية.

عيب الكتلة

وفقًا لتجارب الجسيمات النووية،\((m_{nuc})\) تكون الكتلة الإجمالية للنواة أقل من مجموع كتل النيوكليونات المكونة لها (البروتونات والنيوترونات). يتم تحديد فرق الكتلة، أو العيب الشامل، من خلال

\[\Delta m = Zm_p + (A - Z)m_n - m_{nuc} \label{mass defect} \]

أين\(Zm_p\) الكتلة الكلية للبروتونات،\((A - Z)m_n\) هي الكتلة الكلية للنيوترونات،\(m_{nuc}\) وهي كتلة النواة. وفقًا لنظرية النسبية الخاصة لأينشتاين، فإن الكتلة هي مقياس للطاقة الكلية للنظام (\(E = mc^2\)). وبالتالي، فإن الطاقة الإجمالية للنواة أقل من مجموع طاقات النيوكليونات المكونة لها. لذلك فإن تكوين نواة من نظام من البروتونات والنيوترونات المعزولة هو تفاعل طارد للحرارة - مما يعني أنه يطلق الطاقة. الطاقة المنبعثة أو المشعة في هذه العملية هي\((\Delta m)c^2\).

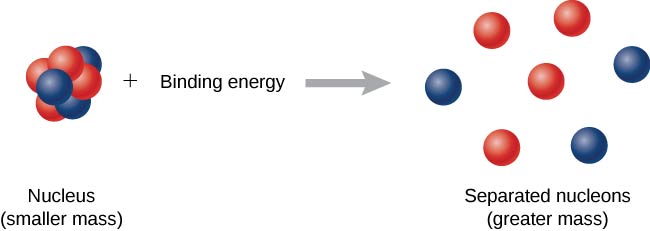
يوضِّح الشكل تفاعلًا. يُظهر LHS نواة بالإضافة إلى طاقة ربط. هذه النواة عبارة عن مجموعة من البروتونات والنيوترونات المكتظة بشكل وثيق ويتم تصنيفها على أنها كتلة أصغر. توجد على RHS نواة ذات بروتونات ونيوترونات معبأة بشكل فضفاض، تسمى نيوكليونات منفصلة، ذات كتلة أكبر. — الشكل\(\PageIndex{1}\): طاقة الربط هي الطاقة المطلوبة لكسر النواة إلى البروتونات والنيوترونات المكونة لها. نظام النيوكليونات المنفصلة له كتلة أكبر من نظام النيوكليونات المرتبطة.

تخيل الآن أن هذه العملية تحدث في الاتجاه المعاكس. بدلاً من تكوين نواة، يتم وضع الطاقة في النظام لتفكيك النواة (الشكل\(\PageIndex{1}\)). تسمى كمية الطاقة المطلوبة طاقة الربط الكلية (BE)،\(E_b\).

تعريف: طاقة الربط

طاقة الربط تساوي كمية الطاقة المنبعثة في تكوين النواة، وبالتالي تُعطى بواسطة

\[E_b = (\Delta m)c^2. \label{BE} \]

تشير النتائج التجريبية إلى أن طاقة الربط للنواة ذات العدد\(A > 8\) الكتلي تتناسب تقريبًا مع إجمالي عدد النيوكليونات في النواة، A. على سبيل المثال\((^{24}Mg)\)، تكون طاقة الربط لنواة المغنيسيوم أكبر مرتين تقريبًا من نواة الكربون\((^{12}C)\).

مثال\(\PageIndex{1}\): Mass Defect and Binding Energy of the Deuteron

احسب العيب الكتلي وطاقة الربط للديوترون. كتلة الديوتيرون هي\(m_D = 3.34359 \times 10^{-27}kg\) أو\(1875.61 \, MeV/c^2\).

الحل

من أجل الديوترون\(Z=1\) و\(A=2\). من المعادلة\ ref {العيب الشامل}، العيب الكتلي للديوترون هو

\[\begin{align*} \Delta m &= m_p + m_n - m_D \\[4pt] &= 938.28 \, MeV/c^2 + 939.57 \, MeV/c^2 - 1875.61 \, MeV/c^2 \\[4pt] &= 2.24 \, MeV/c^2. \end{align*} \nonumber \]

عندئذ تكون طاقة الربط للديوتيرون

\[\begin{align*} E_b &= (\Delta m)c^2 \\[4pt] &= (2.24 \, MeV/c^2)(c^2) \\[4pt] &= 2.24 \, MeV. \end{align*} \nonumber \]

هناك حاجة إلى أكثر من مليوني فولت إلكترون لتقسيم الديوترون إلى بروتون ونيوترون. تشير هذه القيمة الكبيرة جدًا إلى القوة الكبيرة للقوة النووية. وبالمقارنة، فإن أكبر كمية من الطاقة المطلوبة لتحرير إلكترون مرتبط بذرة هيدروجين بقوة كولوم الجذابة (قوة كهرومغناطيسية) تبلغ حوالي 10 eV.

رسم بياني لطاقة الربط لكل نواة

في الفيزياء النووية، واحدة من أهم الكميات التجريبية هي طاقة الربط لكل نواة (BEN)، والتي يتم تحديدها من خلال

\[BEN = \dfrac{E_b}{A} \label{BEN} \]

هذه الكمية هي متوسط الطاقة المطلوبة لإزالة نواة فردية من نواة - مماثلة لطاقة التأين للإلكترون في الذرة. إذا كان BEN كبيرًا نسبيًا، تكون النواة مستقرة نسبيًا. يتم تقدير قيم BEN من تجارب التشتت النووي.

يوجد في الشكل رسم بياني لطاقة الربط لكل نواة مقابل العدد الذري A\(\PageIndex{2}\). يعتبر العديد من علماء الفيزياء هذا الرسم البياني أحد أهم الرسوم البيانية في الفيزياء. ملاحظتان في الترتيب. أولاً، تتراوح قيم BEN النموذجية من 6 إلى 10 MeV، بمتوسط قيمة يبلغ حوالي 8 MeV. بعبارة أخرى، يتطلب الأمر عدة ملايين من فولت الإلكترون لاستخراج نواة من نواة نموذجية، مقارنة بـ 13.6 eV فقط لتأين إلكترون في الحالة الأرضية للهيدروجين. هذا هو السبب في أن القوة النووية يشار إليها باسم القوة النووية «القوية».

ثانيًا، يرتفع الرسم البياني عند المستوى المنخفض A، ويبلغ ذروته بالقرب من الحديد\((Fe, \, A = 56)\)، ثم يتناقص عند ارتفاع\(A\). تشير قيمة الذروة إلى أن نواة الحديد هي النواة الأكثر استقرارًا في الطبيعة (ولهذا السبب أيضًا ينتهي الاندماج النووي في نوى النجوم بـ Fe). يرجع سبب ارتفاع الرسم البياني وانخفاضه إلى القوى المتنافسة في النواة. عند انخفاض القيم\(A\)، تهيمن القوى النووية الجذابة بين النيوكليونات على القوى الكهروستاتيكية الطاردة بين البروتونات. ولكن عند القيم العالية\(A\)، تبدأ القوى الكهروستاتيكية الطاردة بين القوى في الهيمنة، وتميل هذه القوى إلى تفتيت النواة بدلاً من تماسكها معًا.

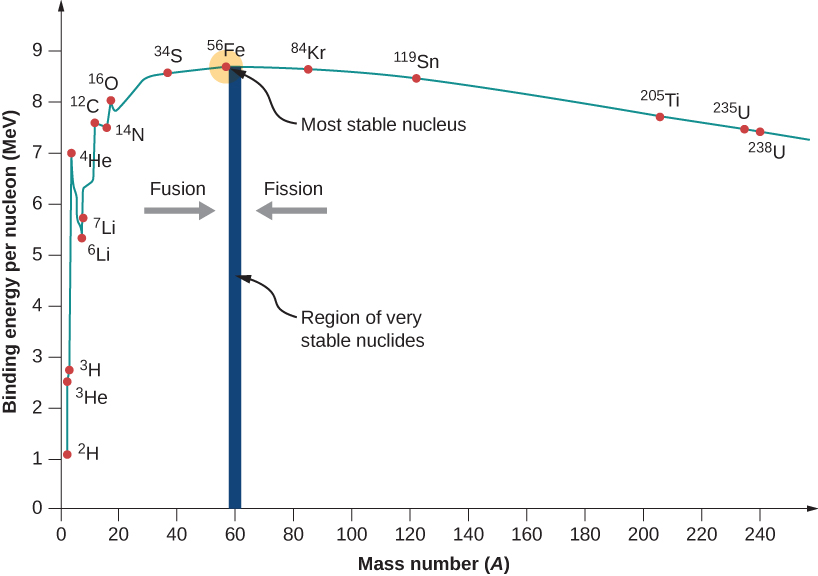
رسم بياني لطاقة الربط لكل نواة، MeV، مقابل رقم الكتلة A. يبدأ الرسم البياني بالقرب من النقطة 2,1 ويصل إلى ذروته بالقرب من العنصر 56 Fe، الذي تبلغ قيمة MeV ما بين 8 و 9. بعد ذلك، يتناقص الرسم البياني إلى قيمة MeV تبلغ تقريبًا 7. 56 Fe تسمى النواة الأكثر استقرارًا. يُطلق على الشريط الرأسي عند A = 60 منطقة من النويدات المستقرة جدًا. يحتوي كلا جانبي هذا الشريط على سهم يشير إليه. يُطلق على اليسار اسم الاندماج والآخر الأيمن يسمى الانشطار. — الشكل\(\PageIndex{2}\): في هذا الرسم البياني لطاقة الربط لكل نواة للنواة المستقرة، يكون BEN هو الأكبر بالنسبة للنواة ذات الكتلة القريبة\(^{56}Fe\). لذلك، فإن اندماج النوى بأعداد كتلة أقل بكثير من Fe، وانشطار النوى بأعداد كتلة أكبر من Fe، هي عمليات طاردة للحرارة.

كما سنرى، يشير الرسم البياني Ben-vers-A إلى أن النوى المقسمة أو المجمعة تطلق كمية هائلة من الطاقة. هذا هو الأساس لمجموعة واسعة من الظواهر، من إنتاج الكهرباء في محطة الطاقة النووية إلى ضوء الشمس.

مثال\(\PageIndex{2}\): Tightly Bound Alpha Nuclides

احسب طاقة الربط لكل نواة من\(^4He \, (\alpha \, particle)\).

إستراتيجية

أوجد طاقة الربط الكلية (BE) باستخدام المعادلة\(BE = (\Delta m)c^2\)،\(\Delta m\) أين العيب الكتلي. يتم تقسيم طاقة الربط لكل نواة (BEN) على\(A\) (المعادلة\ ref {BEN}).

الحل

من أجل\(^4He\)، لدينا\(Z = N = 2\). إجمالي طاقة الربط (المعادلة\ ref {BE}) هو

\[BE = {[2m_p + 2m_n] - m(^4He)}c^2. \nonumber \]

هذه الجماهير هي\(m(^4He) = 4.002602 \, u\)،\(m_p = 1.007825 \, u\)، و\(m_n = 1.008665 \, u\). وهكذا لدينا

\[BE = (0.030378 \, u)c^2. \nonumber \]

مع ملاحظة\(1 \, u = 931.5 \, MeV/c^2\) ذلك، نجد

\[\begin{align*} BE &= (0.030378)(931.5 \, MeV/c^2)c^2 \\[4pt] &= 28.3 \, MeV. \end{align*} \nonumber \]

نظرًا لأن\(A = 4\) إجمالي طاقة الربط لكل نواة (المعادلة\ ref {BEN}) هو

\[BEN = 7.07 \, MeV/nucleon. \nonumber \]

الأهمية

لاحظ أن طاقة الارتباط لكل نواة أكبر\(^4He\) بكثير من نظائر الهيدروجين (\(\approx 3 \, MeV/nucleon\)). لذلك، لا تستطيع نوى الهيليوم تكسير نظائر الهيدروجين دون وضع الطاقة في النظام.

التمارين\(\PageIndex{2}\)

إذا كانت طاقة الربط لكل نواة كبيرة، فهل هذا يجعل من الصعب أو الأسهل نزع نواة من النواة؟

إجابة: أصعب