10.2: خصائص النواة

Last updated
Save as PDF

Page ID: 196721

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

وصف تكوين وحجم النواة الذرية
استخدم رمزًا نوويًا للتعبير عن تكوين نواة ذرية
اشرح لماذا يكون عدد النيوترونات أكبر من البروتونات في النوى الثقيلة
احسب الكتلة الذرية لعنصر بمعلومية نظائره

تتكون النواة الذرية من البروتونات والنيوترونات (الشكل\(\PageIndex{1}\)). تحتوي البروتونات والنيوترونات على نفس الكتلة تقريبًا، لكن البروتونات تحمل وحدة واحدة من الشحنة الموجبة (+e) ولا تحمل النيوترونات أي شحنة. يتم تجميع هذه الجسيمات معًا في مساحة صغيرة جدًا في مركز الذرة. وفقًا لتجارب التشتت، تكون النواة كروية أو بيضاوية الشكل، ويبلغ حجمها حوالي 1/100000 من حجم ذرة الهيدروجين. إذا كانت الذرة بحجم ملعب بيسبول دوري رئيسي، فستكون النواة بحجم كرة البيسبول تقريبًا. تسمى البروتونات والنيوترونات داخل النواة النيوكليونات.

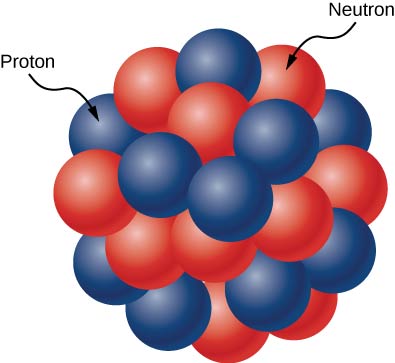
يوضِّح الشكل مجموعة من الكرات الحمراء والزرقاء متجمّعة معًا بشكل وثيق. تُسمى الكرات الحمراء بالنيوترونات والكرات الزرقاء بالبروتونات. — الشكل\(\PageIndex{1}\): تتكون النواة الذرية من البروتونات والنيوترونات. تظهر البروتونات باللون الأزرق، والنيوترونات باللون الأحمر.

تعداد النيوكليونات

يتم تحديد عدد البروتونات في النواة من خلال العدد الذري,\(Z\). عدد النيوترونات في النواة هو رقم النيوترون,\(N\). إجمالي عدد النيوكليونات هو العدد الشامل،\(A\). ترتبط هذه الأرقام بـ

\[A = Z + N. \nonumber \]

يتم تمثيل النواة بشكل رمزي من خلال

\[_Z^AX, \nonumber \]

حيث\(X\) يمثل العنصر الكيميائي،\(A\) هو العدد الكتلي،\(Z\) وهو العدد الذري. على سبيل المثال،\(_6^{12}C\) يمثل نواة الكربون بستة بروتونات وستة نيوترونات (أو 12 نيوكليون).

يظهر الرسم البياني لعدد N من النيوترونات مقابل\(Z\) عدد البروتونات لمجموعة من النوى المستقرة (النويدات s) في الشكل\(\PageIndex{2}\). بالنسبة لقيمة معينة\(Z\)، تكون القيم المتعددة لـ\(N\) (النقاط الزرقاء) ممكنة. بالنسبة للقيم الصغيرة لـ\(Z\)، فإن عدد النيوترونات يساوي عدد البروتونات\((N = P)\) وتقع البيانات على الخط الأحمر. بالنسبة للقيم الكبيرة لـ\(Z\)، يكون عدد النيوترونات أكبر من عدد البروتونات\((N > P)\) وتقع نقاط البيانات فوق الخط الأحمر. يكون عدد النيوترونات بشكل عام أكبر من عدد البروتونات الخاصة بـ\(Z > 15\).

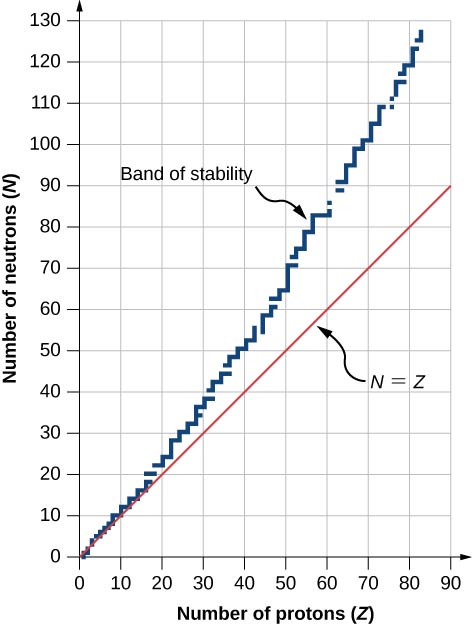
رسم بياني يوضح عدد النيوترونات، N مقابل عدد البروتونات، Z. الخط المستقيم على الرسم البياني يسمى N يساوي Z. ويسمى الخط المسنن الآخر نطاق الثبات. يحتوي هذا على خطوات تدريجية. يبدأ من الأصل. عند Z = 80، قيمة N هي 120. — الشكل\(\PageIndex{2}\): يرسم هذا الرسم البياني عدد النيوترونات N مقابل عدد البروتونات Z للنواة الذرية المستقرة. تحتوي النوى الأكبر على نيوترونات أكثر من البروتونات.

يوجد في الشكل مخطط يستند إلى هذا الرسم البياني يوفر معلومات أكثر تفصيلاً عن كل نواة\(\PageIndex{3}\). هذا المخطط يسمى مخطط النويدات. تمثل كل خلية أو بلاطة نواة منفصلة. يتم ترتيب النوى بترتيب تصاعدي Z (على طول الاتجاه الأفقي) وتصاعدي N (على طول الاتجاه الرأسي).

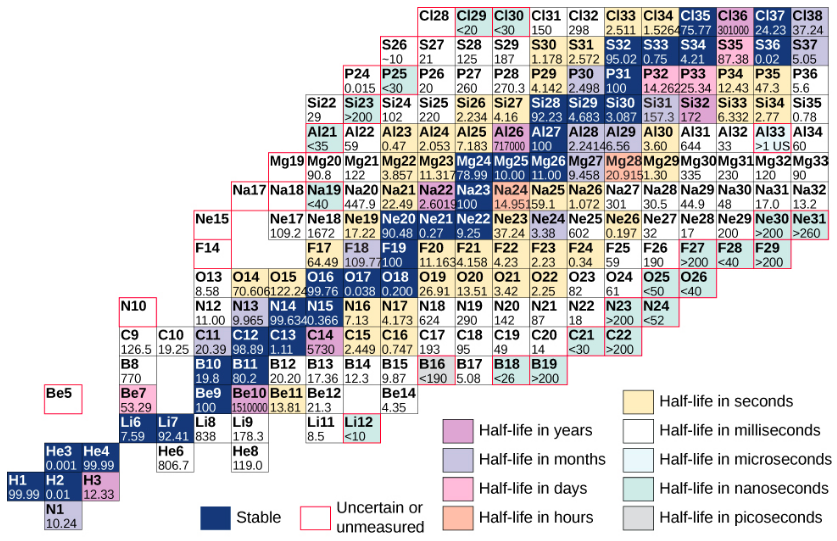يوضِّح الشكل مخططًا للنويدات، بحيث تصاعدُ Z على طول الاتجاه الأفقي وتتصاعد N على طول الاتجاه الرأسي. يتم ترميز الخلايا الموجودة على طول القطر في وسط المخطط بالألوان للإشارة إلى أنها مستقرة. — الشكل\(\PageIndex{3}\): مخطط جزئي للنويدات. بالنسبة للنواة المستقرة (الخلفيات الزرقاء الداكنة)، تمثل قيم الخلايا النسبة المئوية للنواة الموجودة على الأرض بنفس العدد الذري (نسبة الوفرة). بالنسبة للنواة غير المستقرة، يمثل الرقم نصف العمر.

تسمى الذرات التي تحتوي على نوى بنفس عدد البروتونات (Z) وأعداد مختلفة من النيوترونات (N) بالنظائر. على سبيل المثال، يحتوي الهيدروجين على ثلاثة نظائر: الهيدروجين العادي (بروتون واحد، بدون نيوترونات)، الديوتيريوم (بروتون واحد ونيوترون واحد)، والتريتيوم (بروتون واحد واثنين من النيوترونات). تشترك نظائر ذرة معينة في نفس الخصائص الكيميائية، حيث يتم تحديد هذه الخصائص من خلال التفاعلات بين الإلكترونات الخارجية للذرة، وليس النيوكليونات. على سبيل المثال، تبدو المياه التي تحتوي على الديوتيريوم بدلاً من الهيدروجين («الماء الثقيل») وطعمها مثل الماء العادي. يعرض الجدول التالي قائمة بالنظائر الشائعة.

الجدول\(\PageIndex{1}\): النظائر الشائعة
العنصر	الرمز	رقم الكتلة	الكتلة (وحدات الكتلة الذرية)	نسبة الوفرة*	نصف الحياة**
هيدروجين	ح	1	1.0078	99.99	ثابت
	\(^2H\)أو د	2	2.0141	0.01	ثابت
	\(^3H\)	3	3.0160	-	12.32 ص
كربون	\(^{12}C\)	12	12.0000	98.91	ثابت
	\(^{13}C\)	13	13.0034	1.1	ثابت
	\(^{14}C\)	14	14.0032	-	5730 جم
نيتروجين	\(^{14}N\)	14	14.0031	00.6	ثابت
	\(^{15}N\)	15	15.001	0.4	ثابت
	\(^{16}N\)	16	16.0061	-	7.13 ثانية
أكسجين	\(^{16}O\)	16	15.0040	99.76	ثابت
	\(^{17}O\)	17	16.991	0.04	ثابت
	\(^{18}O\)	18	17.992	0.20	ثابت
	\(^{19}O\)	19	19.0035	-	26.46 ثانية
* لا يوجد إدخال إذا كان أقل من 0.001 (مبلغ التتبع). **مستقر في حالة عمر النصف > 10 ثوانٍ.

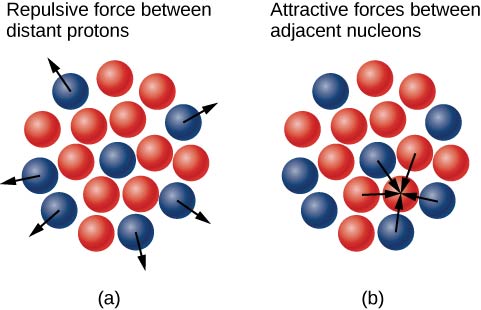
لماذا يفوق عدد النيوترونات عدد البروتونات في النوى الثقيلة (الشكل\(\PageIndex{3}\))؟ تتطلب الإجابة على هذا السؤال فهم القوى داخل النواة باستخدام قوتين أساسيتين كلعبة:

القوة الكهروستاتيكية بعيدة المدى (Coulomb) التي تجعل البروتونات المشحونة إيجابًا تتنافر مع بعضها البعض؛ و
القوة النووية القوية قصيرة المدى التي تجعل كل النيوكليونات في النواة تجذب بعضها البعض.

ربما سمعت أيضًا عن قوة نووية «ضعيفة». هذه القوة مسؤولة عن بعض التحلل النووي، ولكن كما يوحي الاسم، فإنها لا تلعب دورًا في تثبيت النواة مقابل تنافر كولوم القوي الذي تتعرض له. نناقش القوة النووية القوية بمزيد من التفصيل في الفصل التالي عندما نغطي فيزياء الجسيمات. يحدث الاستقرار النووي عندما تعوض القوى الجذابة بين النيوكليونات عن القوى الكهروستاتيكية الطاردة بعيدة المدى بين جميع البروتونات في النواة. بالنسبة للنواة الثقيلة، تعد النيوترونات\((Z > 15)\) الزائدة ضرورية لمنع التفاعلات الكهروستاتيكية من كسر النواة، كما هو موضح في الشكل\(\PageIndex{4}\).

يوضح الشكل أ مجموعة من الدوائر الصغيرة الحمراء والزرقاء. يوجد بروتون أزرق في الوسط محاط بالنيوترونات الحمراء. يوجد المزيد من البروتونات في المحيط، والتي لها سهام تشير إلى الخارج. يوضح الشكل (ب) نفس المجموعة. تُظهر الأسهم كلاً من البروتونات والنيوترونات التي تنجذب نحو نيوترون مجاور. — الشكل\(\PageIndex{4}\): (أ) القوة الكهروستاتيكية مثيرة للاشمئزاز ولها مدى طويل. تمثل الأسهم القوى الخارجية على البروتونات (باللون الأزرق) على السطح النووي بواسطة بروتون (باللون الأزرق أيضًا) في المركز. (ب) تعمل القوة النووية القوية بين النيوكليونات المتجاورة. تمثل الأسهم القوى الجذابة التي يمارسها النيوترون (باللون الأحمر) على أقرب جيرانه.

بسبب وجود نظائر مستقرة، يجب أن نتوخى الحذر بشكل خاص عند اقتباس كتلة العنصر. على سبيل المثال، يحتوي النحاس (Cu) على نظيرين مستقرين:

\[_{29}^{63} Cu ( 62.929595 \, g/mol) \, with \, an \, abundance \, of \, 69.09\% \nonumber \]

\[_{29}^{65} Cu ( 64.927786 \, g/mol) \, with \, an \, abundance \, of \, 30.91\% \nonumber \]

بالنظر إلى هذين «الإصدارين» من Cu، ما كتلة هذا العنصر؟ تُعرَّف الكتلة الذرية للعنصر بأنها المتوسط المرجح لكتل نظائره. وبالتالي، فإن الكتلة الذرية لـ Cu هي

\[m_{Cu} = (62.929595)(0.6909) + (64.927786)(0.3091) = 63.55 \, g/mol. \nonumber \]

غالبًا ما يتم التعبير عن كتلة النواة الفردية بوحدة الكتلة الذرية s (u)، حيث\(u = 1.66054 \times 10^{-27} kg\). (تُعرَّف وحدة الكتلة الذرية بأنها 1/12 كتلة\(^{12}C\) النواة.) في وحدات الكتلة الذرية، تبلغ كتلة نواة الهيليوم (A = 4) حوالي 4 u، وتسمى نواة الهيليوم أيضًا جسيم ألفا (α).

الحجم النووي

إن أبسط نموذج للنواة هو كرة كثيفة من النيوكليونات. وبالتالي فإن\(V\) حجم النواة يتناسب مع عدد النيوكليونات\(A\)، معبرًا عنها بـ

\[V = \dfrac{4}{3} \pi r^3 = kA, \nonumber \]

\(r\)أين نصف قطر النواة\(k\) وهو ثابت بوحدات الحجم. حل المشكلة\(r\)، لدينا

\[r = r_0 A^{1/3} \label{radius} \]

\(r_0\)أين الثابت. بالنسبة للهيدروجين\((A = 1)\)،\(r_0\) يتوافق مع نصف قطر بروتون واحد. تدعم تجارب التشتت هذه العلاقة العامة لمجموعة واسعة من النوى، وتشير إلى أن النيوترونات لها نفس نصف قطر البروتونات تقريبًا. تبلغ القيمة المقاسة تجريبيًا لـ\(r_0\) 1.2 مقياس femtometer تقريبًا (تذكر ذلك\(1 \, fm = 10^{-15}m\)).

مثال\(\PageIndex{1}\): The Iron Nucleus

أوجد نصف القطر (r) والكثافة\((\rho)\) التقريبية لنواة Fe-56. افترض أن كتلة نواة Fe-56 تبلغ حوالي 56 u.

إستراتيجية

العثور على نصف القطر\(^{56}Fe\) هو تطبيق مباشر لـ\(r = r_0A^{1/3}\)، المُعطى\(A = 56\).
لإيجاد الكثافة التقريبية لهذه النواة، افترض أن النواة كروية. احسب حجمه باستخدام نصف القطر الموجود في الجزء (أ)، ثم أوجد الكثافة منه\(\rho = m/V\).

الحل

يُعطى نصف قطر النواة بالمعادلة\ ref {adius}. استبدال القيم\(r_0\) بعوائد A\[\begin{align} r &= (1.2 \, fm)(56)^{1/3} \nonumber \\[4pt] &= (1.2 \, fm)(3.83) \nonumber \\[4pt] &= 4.6 \, fm.\nonumber \end{align} \nonumber \]
تُعرّف الكثافة بأنها\(\rho = m/V\)، أي كرة نصف قطرها r تعني\[\rho = \dfrac{m}{V} = \dfrac{m}{(4/3)\pi r^3}. \nonumber \] استبدال القيم المعروفة\[\begin{align} \rho &= \dfrac{56 \, u}{(1.33)(3.14)(4.6 \, fm)^3} \nonumber \\[4pt] &= 0.138 \, u/fm^3. \nonumber \end{align} \nonumber \] بالتحويل إلى وحدات من\(kg/m^3\)، نجد\[\begin{align} \rho &= (0.138 \, u/fm^3)(1.66 \times 10^{-27} kg/u)\left(\frac{1 \, fm}{10^{-15}m}\right) \nonumber \\[4pt] &= 2.3 \times 10^{17} \, kg/m^3. \nonumber \end{align} \nonumber \]

الأهمية

وجد أن نصف قطر نواة Fe-56 يبلغ حوالي 5 سم، لذلك يبلغ قطرها حوالي 10 سم، أو\(10^{-14} m\). في المناقشات السابقة لتجارب التشتت التي أجراها روثرفورد، تم تقدير قطر نواة الضوء.\(10^{-15}m\) لذلك، تكون النتيجة المعروضة للنواة متوسطة الحجم معقولة.
قد تبدو الكثافة الموجودة هنا مذهلة. ومع ذلك، فإنه يتفق مع التعليقات السابقة حول النواة التي تحتوي على كل كتلة الذرة تقريبًا في منطقة صغيرة من الفضاء. المتر المكعب من المادة النووية له نفس كتلة مكعب الماء 61 كم على كل جانب.

التمارين الرياضية\(\PageIndex{1}\)

النواة X أكبر بمرتين من النواة Y. ما نسبة كتلتها الذرية؟

إجابة: ثمانية