10.5: التفاعلات النووية
- Page ID
- 196715
في نهاية هذا القسم، ستكون قادرًا على:
- وصف ومقارنة ثلاثة أنواع من الإشعاع النووي
- استخدم الرموز النووية لوصف التغييرات التي تحدث أثناء التفاعلات النووية
- وصف العمليات المتضمنة في سلسلة اضمحلال العناصر الثقيلة
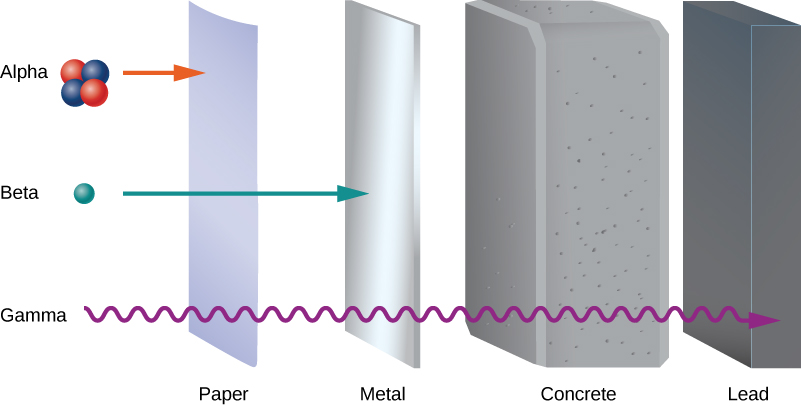
كشفت التجارب المبكرة عن ثلاثة أنواع من «الأشعة» النووية أو الإشعاع: ألفا\((\alpha)\) rays\((\beta)\) rays وبيتا وغاما\((\gamma)\) rays. تختلف هذه الأنواع الثلاثة من الإشعاع من خلال قدرتها على اختراق المادة. بالكاد تستطيع أشعة ألفا المرور عبر ورقة رقيقة. يمكن لإشعاع بيتا اختراق الألومنيوم إلى عمق حوالي 3 مم، ويمكن أن تخترق أشعة جاما الرصاص إلى عمق 2 سم أو أكثر (الشكل\(\PageIndex{1}\)).
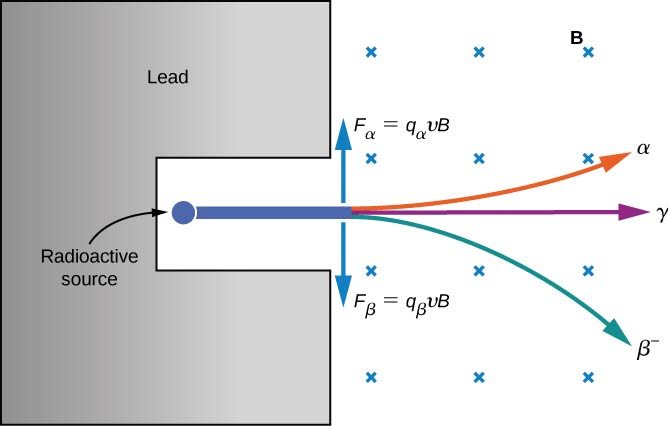
يتم فحص الخواص الكهربائية لهذه الأنواع الثلاثة من الإشعاع من خلال تمريرها عبر مجال مغناطيسي منتظم، كما هو موضح في الشكل\(\PageIndex{2}\). وفقًا لمعادلة القوة المغناطيسية لشحنة متحركة في مجال مغناطيسي
\[\vec{F} = q\vec{v} \times \vec{B} \nonumber \]
حيث تنحرف الجسيمات المشحونة إيجابًا لأعلى، وتنحرف الجسيمات سالبة الشحنة إلى الأسفل، وتمر الجسيمات بدون شحنة عبر المجال المغناطيسي دون أن تتأثر. في النهاية، تم التعرف على\(\alpha\) الأشعة باستخدام نوى الهيليوم\((^4He)\)،\(\beta\) والأشعة ذات الإلكترونات والبوزيترونات (الإلكترونات الموجبة الشحنة أو مضادات الإلكترونات)،\(\gamma\) والأشعة ذات الفوتونات عالية الطاقة. نناقش أشعة ألفا وبيتا وغاما بالتفصيل في بقية هذا القسم.
ألفا ديكاي
تصدر النوى الثقيلة غير المستقرة\(\alpha\) إشعاعًا. في تحلل\(\alpha\) الجسيمات (أو اضمحلال ألفا)، تفقد النواة بروتونين ونيوترونين، وبالتالي ينخفض العدد الذري بمقدار اثنين، بينما يتناقص عدد كتلتها بمقدار أربعة. قبل الاضمحلال، كانت النواة تسمى النواة الأم. يشار إلى النواة أو النواة المنتجة في الاضمحلال بالنواة الابنة أو نواة الابنة. نحن نمثل\(\alpha\) الاضمحلال بشكل رمزي من خلال
\[\ce{_Z^AX \rightarrow _{Z-2}^{A-4}X + _2^4He} \label{alpha} \]
أين\(_Z^AX\) النواة الأم،\(_{Z-2}^{A-4}X\) هي النواة البنت،\(_2^4He\) وهي\(\alpha\) الجسيم. في\(\alpha\) حالة الاضمحلال، تتحلل نواة العدد الذري Z إلى نواة العدد\(Z - 2\) الذري والكتلة الذرية\(A - 4\). ومن المثير للاهتمام أن حلم الكيميائيين القدماء بتحويل معادن أخرى إلى ذهب ممكن علميًا من خلال عملية تحلل ألفا. فشلت جهود الكيميائيين لأنهم اعتمدوا على التفاعلات الكيميائية بدلاً من التفاعلات النووية.
شاهد جزيئات ألفا وهي تهرب من نواة البولونيوم، مما يتسبب في تحلل ألفا الإشعاعي. شاهد كيف ترتبط أوقات الاضمحلال العشوائي بنصف العمر. لتجربة محاكاة تحلل ألفا، قم بزيارة جسيمات ألفا
مثال على تحلل ألفا هو اليورانيوم 238:
\[\ce{_{92}^{238}U \rightarrow _{90}^{234}X + _2^4He} \nonumber \]
انخفض العدد الذري من 92 إلى 90. العنصر الكيميائي الذي يحتوي عليه\(Z = 90\) هو الثوريوم. ومن ثم، فقد تحلل اليورانيوم 238 إلى الثوريوم 234 بانبعاث\(\alpha\) جسيم، مكتوب
\[\ce{_{92}^{238}U \rightarrow _{90}^{234}Th + _2^4He} \nonumber \]
\(_{90}^{234}Th\)ويتحلل بعد ذلك\(\beta\) بالانبعاثات بعمر نصف يبلغ 24 يوماً. تأخذ الطاقة المنبعثة في تحلل ألفا هذا شكل الطاقات الحركية لنوى الثوريوم والهيليوم، على الرغم من أن الطاقة الحركية للثوريوم أصغر من الهيليوم بسبب كتلته الثقيلة وسرعته الأصغر.
\(^{230}Pu\)يمكن إيجاد الطاقة المنبعثة في\(\alpha\) الاضمحلال باستخدام المعادلة\(E = (\Delta m)c^2\). يجب أن نجد\(\Delta m\) أولاً الفرق في الكتلة بين النواة الأم ومنتجات الاضمحلال.
الحل
معادلة الاضمحلال هي
\[\ce{^{230}Pu \rightarrow ^{235}U + ^4He}. \nonumber \]
وبالتالي، فإن الكتل ذات الصلة هي تلك\(\alpha\) الخاصة بالجسيم أو\(^4He\) جميعها معروفة.\(^{230}Pu\)\(^{235}U\) كانت الكتلة الأولية\(m(^{230}Pu) = 230.052157 \, u\). الكتلة النهائية هي المجموع
\[\ce{m(^{235}U) + m(^4He) = 235.043924 \, u + 4.002602 \, u} \nonumber \]
وهكذا،
\[ \ce{\Delta m = m(^{230}Pu) - [m(^{235}U) + m(^4He)]} \nonumber \]
\[= 239.052157 \, u - 239.046526 \, u \nonumber \]
\[= 0.0005631 \, u. \nonumber \]
الآن يمكننا العثور على E عن طريق\(\Delta m\) الدخول في المعادلة:
\[E = (\Delta m) c^2 = (0.005631 \, u)c^2. \nonumber \]
نحن نعلم\(1 \, u = 931.5 \, MeV/c^2\)، لذلك لدينا
\[\begin{align} E & = (0.005631)(931.5 \, MeV/c^2)(c^2) \nonumber \\[4pt] &= 5.25 \, MeV. \nonumber \end{align} \nonumber \]
الأهمية
الطاقة المنبعثة من هذا\(\alpha\) الاضمحلال تقع في نطاق MeV، وهي أكبر بعدة مرات من طاقات التفاعل الكيميائي. تصبح معظم هذه الطاقة طاقة حركية\(\alpha\) للجسيم (أو\(^4He\) النواة)، الذي يتحرك بعيدًا بسرعة عالية. الطاقة التي يحملها ارتداد\(^{235}U\) النواة أصغر بكثير بسبب كتلتها الكبيرة نسبيًا. يمكن ترك\(^{235}U\) النواة في حالة مثيرة لإصدار فوتونات (\(\gamma\)أشعة) لاحقًا. 239 وحدة حرارية بريطانية ← 235 يو + 4 هو.
بيتا ديكاي
في معظم\(\beta\) حالات تحلل الجسيمات (أو تحلل بيتا)، ينبعث إما إلكترون (\(\beta^-\)) أو بوزيترون (\(\beta^+\)) من نواة. للبوزيترون نفس كتلة الإلكترون، لكن شحنته هي\(+e\). لهذا السبب، يُطلق على البوزيترون أحيانًا اسم مضاد الإلكترون. كيف يحدث\(\beta\) التسوس؟ التفسير المحتمل هو أن الإلكترون (البوزيترون) يقتصر على النواة قبل الاضمحلال ويهرب بطريقة أو بأخرى. للحصول على تقدير تقريبي لطاقة الهروب، ضع في اعتبارك نموذجًا مبسطًا لإلكترون محاصر في صندوق (أو في مصطلحات ميكانيكا الكم، بئر مربع أحادي البعد) بعرض نواة نموذجية (\(10^{-14}\)). وفقًا لمبدأ عدم اليقين لهايزنبرغ في ميكانيكا الكم، فإن عدم اليقين في زخم الإلكترون هو:
\[\begin{align} \Delta p &\ge \dfrac{h}{\Delta x} \nonumber \\[4pt] &= \dfrac{6.6 \times 10^{-34} m^2 \cdot kg/s}{10^{-14}m} \nonumber \\[4pt] &= 6.6 \times 10^{-20} kg \cdot m/s. \end{align} \nonumber \]
إذا أخذنا قيمة الزخم هذه (التقدير الناقص) على أنها «القيمة الحقيقية»، فإن الطاقة الحركية للإلكترون عند الهروب تكون تقريبًا
\[\begin{align} \dfrac{(\Delta p)^2}{2m_e} &= \dfrac{6.6 \times 10^{-20} m^2 \cdot kg/s)^2}{2(9.1 \times 10^{-31}kg)} \nonumber \\[4pt] &= 2.0 \times 10^{-9} J \nonumber \\[4pt] &= 12,400 \, MeV. \end{align} \nonumber \]
من الناحية التجريبية، وجد أن الإلكترونات المنبعثة في\(\beta^-\) الاضمحلال تحتوي على طاقات حركية في حدود عدد قليل من MeV. لذلك نستنتج أن الإلكترون يتم إنتاجه بطريقة ما في الاضمحلال بدلاً من الهروب من النواة. يتم وصف إنتاج الجسيمات (الإبادة) من خلال النظريات التي تجمع بين ميكانيكا الكم والنسبية، وهو موضوع دورة أكثر تقدمًا في الفيزياء.
يتضمن تحلل بيتا النووي تحويل نواة إلى أخرى. على سبيل المثال، يمكن للنيوترون أن يتحلل إلى بروتون عن طريق انبعاث إلكترون (\(\beta^-\)) وجسيم عديم الكتلة تقريبًا يسمى مضاد النيوترينو (\(\overline{\nu}\)):
\[\ce{_0^1n \rightarrow _1^1p + _1^0e + \overline{\nu}. } \nonumber \]
\(_{-1}^0e\)يتم استخدام الترميز لتعيين الإلكترون. ورقمها الكتلي هو 0 لأنها ليست نواة، ورقمها الذري يعني أنها تحتوي على شحنة مقدارها\(-e\).\(-1\) يتم تمثيل البروتون\(_1^1p\) لأن عدد كتله ورقمه الذري هما 1. عندما يحدث هذا داخل نواة ذرية، لدينا المعادلة التالية لتحلل بيتا:
\[\ce{_z^AX \rightarrow _{Z+1} ^AX + _1^0e + \overline{\nu}.} \label{beta} \]
تحدث هذه العملية بسبب القوة النووية الضعيفة.
شاهد تحلل بيتا يحدث لمجموعة من النوى أو لنواة فردية.
على سبيل المثال،\(_{90}^{234}Th\) يكون النظير غير مستقر ويتحلل\(\beta^-\) بالانبعاث بعمر نصف يبلغ 24 يومًا. يمكن تمثيل تسوسها على النحو التالي:
\[\ce{_{90}^{234}Th \rightarrow _{91}^{234}X + _1^0e^+ + \overline{\nu}.} \nonumber \]
نظرًا لأن العنصر الكيميائي ذو الرقم الذري 91 هو البروتكتينيوم (Pa)، يمكننا كتابة\(\beta^-\) تحلل الثوريوم على النحو التالي
\[\ce{_{90}^{234}Th \rightarrow _{91}^{234}Pa + _1^0e^+ + \overline{\nu}.} \nonumber \]
العملية العكسية ممكنة أيضًا: يمكن أن يتحلل البروتون إلى نيوترون عن طريق انبعاث بوزيترون (\(e^+\)وجسيم عديم الكتلة تقريبًا يسمى النيوترين o (\(v\)). تمت كتابة رد الفعل هذا كـ
\[\ce{_1^1p \rightarrow _0^1n + _{+1}^0e + \nu.} \nonumber \]
\(_1^0e\)وينبعث البوزيترون مع النيوترينو\(\nu\)، ويبقى النيوترون في النواة. (مثل\(\beta^-\) الاضمحلال، لا يسبق البوزيترون الاضمحلال ولكن يتم إنتاجه في الاضمحلال.) بالنسبة للبروتون المعزول، تكون هذه العملية مستحيلة لأن النيوترون أثقل من البروتون. ومع ذلك، فإن هذه العملية ممكنة داخل النواة لأن البروتون يمكنه استقبال الطاقة من النيوكليونات الأخرى للانتقال. كمثال,\(_{13}^{26}Al\) يتحلل نظير الألومنيوم\(\beta^+\) بالانبعاث بعمر نصف يبلغ\(7.40 \times 10^5 y\). تمت كتابة الاضمحلال على النحو التالي
\[\ce{_{13}^{26}Al \rightarrow _{12}^{26}X + _1^0e + \nu.} \nonumber \]
الرقم الذري 12 يتوافق مع المغنيسيوم. وبالتالي،
\[\ce{_{13}^{26}Al \rightarrow _{12}^{26}Mg + _1^0 e + \nu.} \nonumber \]
كتفاعل نووي، يمكن كتابة انبعاث البوزيترون على النحو التالي:
\[\ce{_Z^AX \rightarrow _{Z-1} ^AX + _1^{0} e + \nu.} \nonumber \]
لم يتم اكتشاف النيوترينو في التجارب المبكرة على\(β\) الاضمحلال. ومع ذلك، يبدو أن قوانين الطاقة والزخم تتطلب مثل هذا الجسيم. في وقت لاحق، تم اكتشاف النيوترينوات من خلال تفاعلاتها مع النوى.
تخضع\(_{83}^{211}Bi\) النواة لكليهما\(\alpha\)\(\beta^-\) وتتحلل. لكل حالة، ما هي نواة الابنة؟
إستراتيجية
يمكننا استخدام العمليات الموضحة بواسطة المعادلة\ ref {alpha} والمعادلة\ ref {beta}، بالإضافة إلى الجدول الدوري، لتحديد العناصر الناتجة.
الحل
العدد الذري والعدد الكتلي\(\alpha\) للجسيم هما 2 و 4 على التوالي. وهكذا، عندما تصدر نواة البزموت 211\(\alpha\) جسيمًا، يكون العدد الذري للنواة البنت 81 وعدد كتلتها 207. العنصر الذي يبلغ رقمه الذري 81 هو الثاليوم، لذلك يتم إعطاء الاضمحلال بواسطة
\[\ce{_{83}^{211}Bi \rightarrow _{81}^{207} Ti + _2^4He.} \nonumber \]
في\(\beta^-\) حالة الاضمحلال، يزداد العدد الذري بمقدار 1، بينما يظل العدد الكتلي كما هو. العنصر الذي يبلغ رقمه الذري 84 هو البولونيوم، لذلك يتم إعطاء الاضمحلال بواسطة
\[\ce{_{83}^{211}Bi \rightarrow _{84}^{211}Po + _{-1}^0e + \overline{\nu}.} \nonumber \]
في حالة تحلل بيتا الإشعاعي، هل يزيد أو ينقص عدد الكتلة الذرية A؟
الحل
لا أحد منهما؛ يبقى على حاله.
جاما ديكاي
يمكن للنواة في حالة الإثارة أن تتحلل إلى حالة منخفضة المستوى عن طريق انبعاث فوتون «أشعة جاما»، ويعرف هذا باسم تحلل جاما. هذا يماثل إزالة الإثارة للإلكترون الذري. يتم تمثيل تحلل جاما بشكل رمزي من خلال
\[\ce{_{Z}^{A}X}^{*} \ce{\rightarrow _{Z}^{A}X + \gamma} \label{gamma} \]
حيث تشير العلامة النجمية (*) على النواة إلى حالة الإثارة. في\(\gamma\) حالة الاضمحلال، لا يتغير الرقم الذري ولا عدد الكتلة، لذلك لا يتغير نوع النواة.
سلسلة الاضمحلال الإشعاعي
النواة\(Z > 82\) غير مستقرة وتتحلل بشكل طبيعي. العديد من هذه النوى لها عمر قصير جدًا، لذا فهي غير موجودة في الطبيعة. تشمل الاستثناءات البارزة\(_{90}^{232}Th\) (أو Th-232) مع عمر نصف يبلغ\(1.39 \times 10^{10}\) سنوات، و\(_{92}^{238}U\) (أو U-238) بعمر نصف يبلغ\(7.04 \times 10^8\) سنوات. عندما تتحلل نواة ثقيلة إلى نواة أخف، يمكن أن تصبح نواة الابنة الأخف هي النواة الأم للتحلل التالي، وما إلى ذلك. يمكن أن تنتج هذه العملية سلسلة طويلة من التحلل النووي تسمى سلسلة الاضمحلال. تنتهي السلسلة بنواة مستقرة.
لتوضيح مفهوم سلسلة الاضمحلال، ضع في اعتبارك اضمحلال سلسلة Th-232 (الشكل\(\PageIndex{3}\)). تم رسم الرقم النيوتروني، N، على المحور y الرأسي، والرقم الذري، Z، مرسوم على المحور x الأفقي، لذلك تم العثور على Th-232 عند الإحداثيات\((N, Z) = (142.90)\). يتحلل Th-232\(\alpha\) بالانبعاث بعمر نصف\(1.39 \times 10^{10}\) سنوات. يقلل اضمحلال ألفا العدد الذري بمقدار 2 والعدد الكتلي بمقدار 4، لذلك لدينا
\[\ce{_{90}^{232}Th \rightarrow _{88}^{228}Ra + _2^4He.} \nonumber \]
رقم النيوترون للراديوم-228 هو 140، لذلك يوجد في الرسم التخطيطي عند الإحداثيات\((N,Z) = (140, \, 90)\). الراديوم 228 غير مستقر أيضًا ويتحلل\(\alpha\) بالانبعاث بعمر نصف يبلغ 5.76 عامًا إلى Actinum-228. يزداد العدد الذري بمقدار 1، ويظل رقم الكتلة كما هو، وينخفض عدد النيوترون بمقدار 1. لاحظ أنه في الرسم البياني، يظهر\(α\) الانبعاث كخط منحدر لأسفل إلى اليسار، مع انخفاض كل من N و Z بمقدار 2. من ناحية أخرى، يظهر انبعاث بيتا كخط منحدر لأسفل إلى اليمين مع انخفاض N بمقدار 1 وزيادة Z بمقدار 1. بعد عدة اضمحلال إضافي لألفا وبيتا، تنتهي السلسلة بالنواة المستقرة Pb-208.
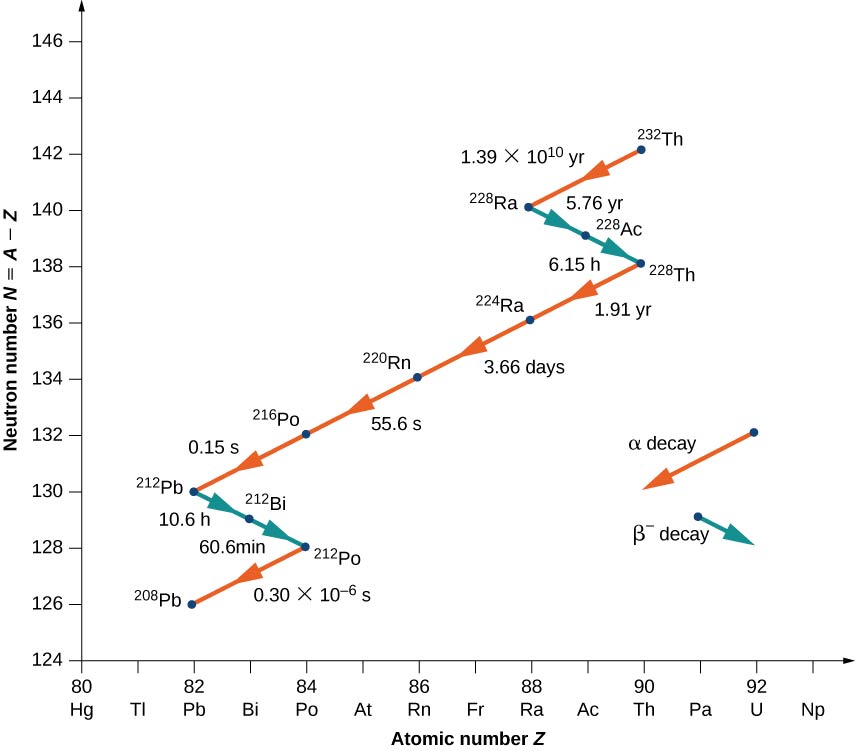
يعتمد التردد النسبي لأنواع مختلفة من التحلل الإشعاعي (ألفا وبيتا وغاما) على العديد من العوامل، بما في ذلك قوة القوى المعنية وعدد الطرق التي يمكن أن يحدث بها تفاعل معين دون انتهاك الحفاظ على الطاقة والزخم. يعتمد عدد المرات التي يحدث فيها التحلل الإشعاعي غالبًا على توازن حساس للقوى القوية والكهرومغناطيسية.
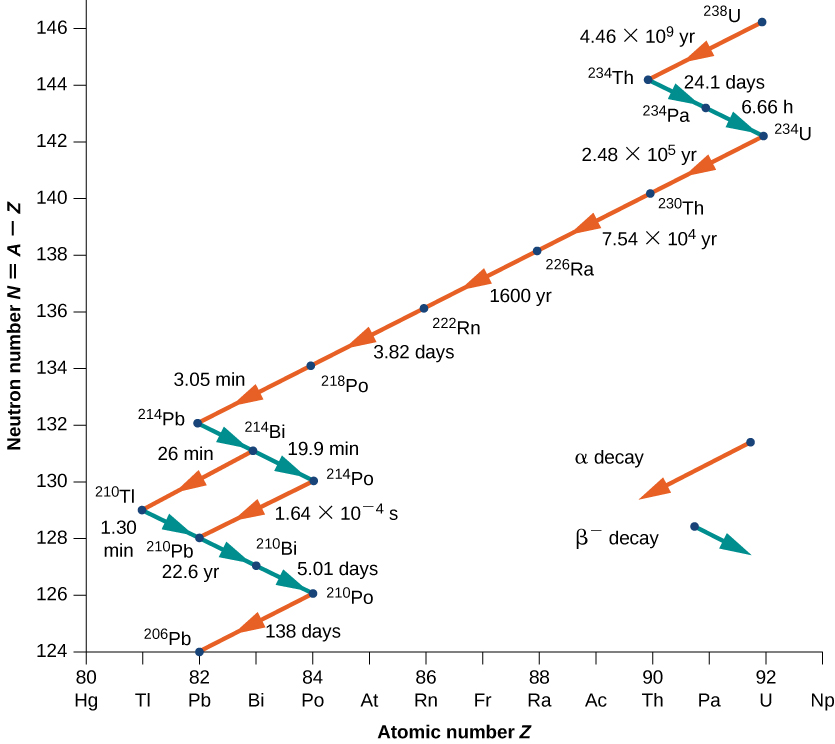
كمثال آخر، ضع في اعتبارك سلسلة اضمحلال U-238 الموضحة في الشكل\(\PageIndex{4}\). بعد العديد من حالات تحلل ألفا وبيتا، تنتهي السلسلة بالنواة المستقرة Pb-206.
يظهر في الشكل مثال على الاضمحلال الذي لم تعد نواته الأم موجودة بشكل طبيعي\(\PageIndex{5}\). يبدأ بالنبتونيوم 237 وينتهي في النواة المستقرة Bismuth-209. يُطلق على النبتونيوم عنصر ترانسوراني لأنه يقع خارج اليورانيوم في الجدول الدوري. يحتوي اليورانيوم على أعلى عدد ذري\((Z + 92)\) من أي عنصر موجود في الطبيعة. \(Z > 92\)لا يمكن إنتاج العناصر إلا في المختبر. من المحتمل أنها كانت موجودة أيضًا في الطبيعة في وقت تكوين الأرض، ولكن بسبب عمرها القصير نسبيًا، فقد تدهورت تمامًا. لا يوجد شيء يختلف جوهريًا بين العناصر التي تحدث بشكل طبيعي والعناصر الاصطناعية.
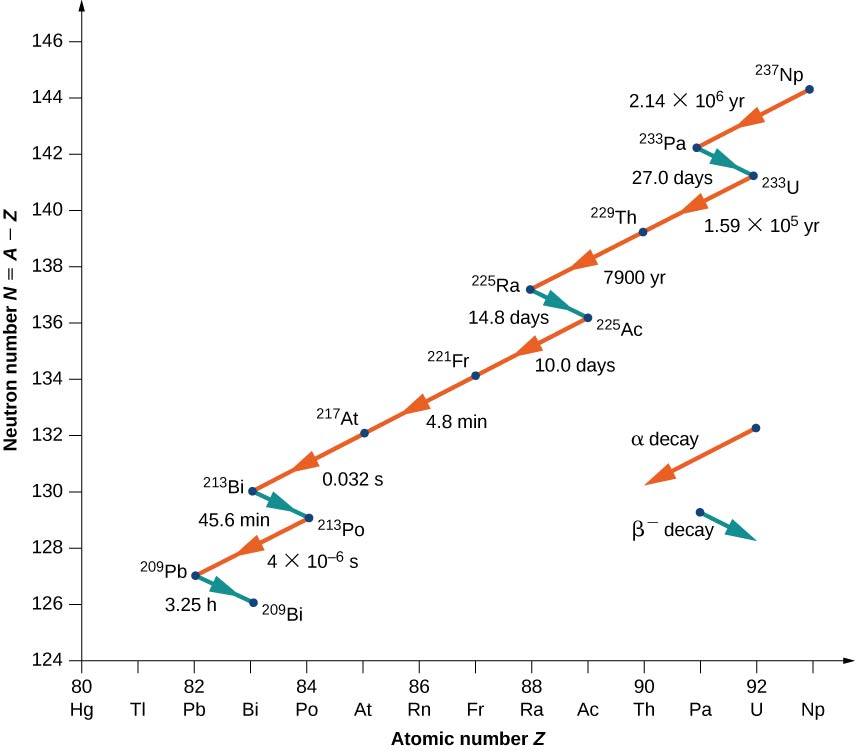
لاحظ أنه بالنسبة لـ Bi (21)، قد يستمر الاضمحلال إما من خلال تحلل ألفا أو بيتا.
النشاط الإشعاعي في الأرض
وفقًا للجيولوجيين، إذا لم يكن هناك مصدر للحرارة، كان يجب أن تبرد الأرض إلى درجة حرارتها الحالية في مدة لا تزيد عن مليار سنة. ومع ذلك، يبلغ عمر الأرض أكثر من 4 مليارات سنة. لماذا تبرد الأرض ببطء شديد؟ الجواب هو النشاط الإشعاعي النووي، أي الجسيمات عالية الطاقة المنتجة في التحلل الإشعاعي تسخن الأرض من الداخل (الشكل\(\PageIndex{6}\)).
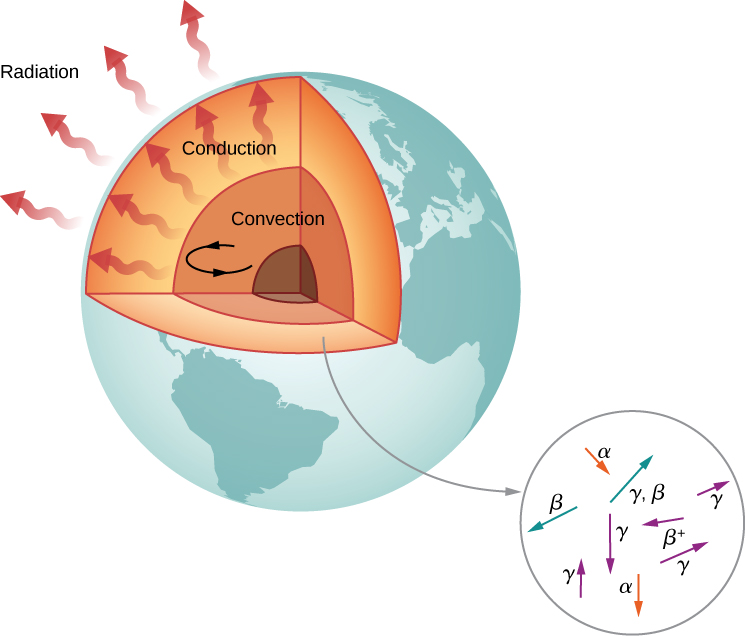
النوى المرشحة لنموذج التسخين هذا هي\(^{238}U\)\(^{40}K\) و التي تمتلك فترات نصف عمر مماثلة لعمر الأرض أو أطول منه. الطاقة الناتجة عن هذا التحلل (في الثانية لكل متر مكعب) صغيرة، لكن الطاقة لا يمكن أن تتسرب بسهولة، لذا فإن قلب الأرض حار جدًا. يتم نقل الطاقة الحرارية في قلب الأرض إلى سطح الأرض وبعيدًا عنها من خلال عمليات الحمل الحراري والتوصيل والإشعاع.


