9.9: الموصلية الفائقة
- Page ID
- 196487
في نهاية هذا القسم، ستكون قادرًا على:
- وصف السمات الرئيسية للموصل الفائق
- وصف نظرية BCS للموصلية الفائقة
- حدد المجال المغناطيسي الحرج لـ T = 0 K من بيانات المجال المغناطيسي
- احسب الحد الأقصى من القوة الدافعة الكهربية أو التيار حتى يظل السلك فائق التوصيل
يمكن اعتبار المقاومة الكهربائية كمقياس لقوة الاحتكاك في تدفق التيار الكهربائي. وبالتالي، تعد المقاومة الكهربائية مصدرًا أساسيًا لتبديد الطاقة في الأنظمة الكهربائية مثل المغناطيسات الكهربائية والمحركات الكهربائية وخطوط النقل. يشيع استخدام الأسلاك النحاسية في الأسلاك الكهربائية لأنها تحتوي على واحدة من أقل المقاومات الكهربائية في درجة حرارة الغرفة بين الموصلات الشائعة. (في الواقع، تتمتع الفضة بمقاومة أقل من النحاس، لكن التكلفة العالية والتوافر المحدود للفضة يفوق مدخراتها في الطاقة مقارنة بالنحاس.)
على الرغم من أن مناقشتنا للموصلية تبدو وكأنها تعني أن جميع المواد يجب أن تتمتع بمقاومة كهربائية، إلا أننا نعلم أن الأمر ليس كذلك. عندما تنخفض درجة الحرارة إلى ما دون القيمة الحرجة للعديد من المواد، تنخفض مقاومتها الكهربائية إلى الصفر، وتصبح المواد موصلات فائقة.
شاهد هذا المقتطف من فيديو نوفا، بعنوان «جعل الأشياء أكثر برودة»، كمقدمة لموضوع الموصلية الفائقة وتطبيقاتها العديدة.
خصائص الموصلات الفائقة
بالإضافة إلى المقاومة الكهربائية الصفرية، تتمتع الموصلات الفائقة أيضًا بمغناطيسية مثالية. بمعنى آخر، في وجود مجال مغناطيسي مطبق، يكون المجال المغناطيسي الصافي داخل الموصل الفائق دائمًا صفرًا (الشكل\(\PageIndex{1}\)). لذلك، يتم طرد أي خطوط مجال مغناطيسي تمر عبر عينة فائقة التوصيل عندما تكون في حالتها الطبيعية بمجرد أن تصبح العينة فائقة التوصيل. هذه هي مظاهر تأثير Meissner، التي تعلمتها في الفصل الخاص بالتيار والمقاومة.
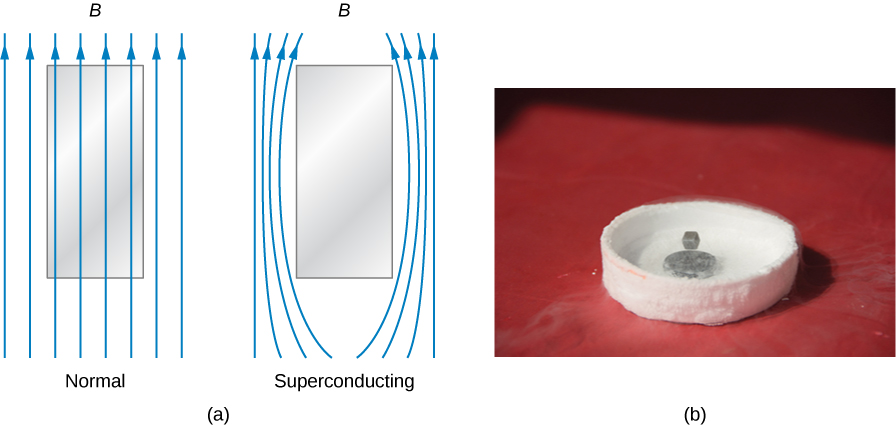
ومن المثير للاهتمام أن تأثير Meissner ليس نتيجة للمقاومة الصفرية. لمعرفة السبب، لنفترض أن العينة الموضوعة في مجال مغناطيسي تمر بمرحلة انتقالية تنخفض فيها مقاومتها إلى الصفر. وفقًا لقانون أوم، ترتبط كثافة التيار، j، في العينة بالحقل الكهربائي الداخلي الصافي، E، والمقاومة\(\rho\) بـ\(j = E/\rho\) If\(\rho\) هي صفر، ويجب أن تكون E أيضًا صفرًا حتى تظل j محدودة. الآن يرتبط E والتدفق المغناطيسي\(\Phi_m\) عبر العينة بقانون فاراداي كـ
\[\oint E\,dI = - \dfrac{d\Phi_m}{dt} \nonumber \]
إذا كان E صفرًا،\(d\Phi_m/dt\) فهو صفر أيضًا، أي أن التدفق المغناطيسي عبر العينة لا يمكن أن يتغير. لذلك يجب عدم طرد خطوط المجال المغناطيسي داخل العينة عند حدوث الانتقال. وبالتالي، لا يعني ذلك أن المادة التي تصل مقاومتها إلى الصفر يجب أن تظهر تأثير Meissner. بدلاً من ذلك، فإن تأثير Meissner هو خاصية خاصة للموصلات الفائقة.
خاصية أخرى مهمة للمادة فائقة التوصيل هي درجة حرارتها الحرجة\(T_c\)، وهي درجة الحرارة التي تقل عنها المادة فائقة التوصيل. يتراوح النطاق المعروف لدرجات الحرارة الحرجة من جزء من 1 K إلى ما يزيد قليلاً عن 100 K. تُعرف الموصلات الفائقة ذات درجات الحرارة الحرجة بالقرب من هذا الحد الأعلى باسم الموصلات الفائقة «ذات درجة الحرارة العالية». من الناحية العملية،\(T_c \gg 77 \, K\) تعتبر الموصلات الفائقة مهمة جدًا بالنسبة لها. في الوقت الحاضر، لا تزال التطبيقات التي تنطوي على الموصلات الفائقة تتطلب غالبًا غمر المواد فائقة التوصيل في الهيليوم السائل (4.2 K) من أجل إبقائها تحت درجة حرارتها الحرجة. يجب تجديد حمامات الهيليوم السائل باستمرار بسبب التبخر، ويمكن أن تفوق تكاليف التبريد بسهولة الوفورات في استخدام موصل فائق. ومع ذلك، فإن 77 K هي درجة حرارة النيتروجين السائل، وهو أكثر وفرة وأقل تكلفة بكثير من الهيليوم السائل. سيكون الأمر أكثر فعالية من حيث التكلفة إذا تمكنا بسهولة من تصنيع واستخدام مكونات الموصلات الفائقة ذات درجة الحرارة العالية والتي تحتاج فقط إلى الاحتفاظ بها في حمامات النيتروجين السائل للحفاظ على الموصلية الفائقة.
يتم حاليًا استخدام المواد فائقة التوصيل ذات درجة الحرارة العالية في تطبيقات مختلفة. ومن الأمثلة على ذلك إنتاج المجالات المغناطيسية في بعض مسرعات الجسيمات. الهدف النهائي هو اكتشاف المواد فائقة التوصيل في درجة حرارة الغرفة. وبدون أي متطلبات تبريد، يمكن أن يكون الجزء الأكبر من المكونات الإلكترونية وخطوط النقل فائقة التوصيل، مما يؤدي إلى زيادات كبيرة وغير مسبوقة في الكفاءة والأداء.
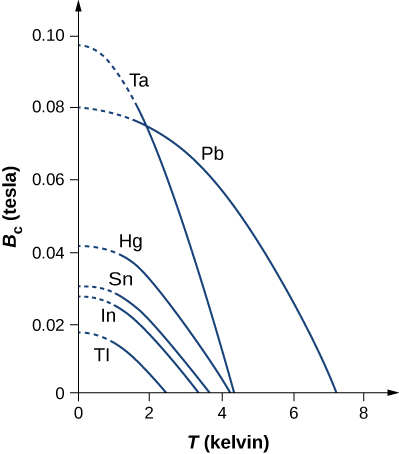
خاصية أخرى مهمة للمادة فائقة التوصيل هي المجال المغناطيسي الحرج\(B_c(T)\)، وهو الحد الأقصى للمجال المغناطيسي المطبق عند درجة حرارة T التي تسمح للمادة بالبقاء فائقة التوصيل. سيؤدي الحقل التطبيقي الأكبر من المجال الحرج إلى تدمير الموصلية الفائقة. يكون المجال الحرج صفرًا عند درجة الحرارة الحرجة ويزداد مع انخفاض درجة الحرارة. يوضح الشكل مخططات المجال الحرج مقابل درجة الحرارة للعديد من المواد فائقة التوصيل\(\PageIndex{2}\). يمكن وصف الاعتماد على درجة الحرارة في المجال الحرج تقريبًا من خلال
\[B_c(T) = B_c(0) \left[1 - \left(\frac{T}{T_c}\right)^2\right] \nonumber \]
\(B_0\)أين المجال الحرج عند درجة حرارة الصفر المطلقة. \(\PageIndex{1}\)يسرد الجدول درجات الحرارة والمجالات الحرجة لفئتين من الموصلات الفائقة: الموصل الفائق من النوع الأول والموصل الفائق من النوع الثاني. بشكل عام، تعتبر الموصلات الفائقة من النوع الأول عناصر، مثل الألومنيوم والزئبق. وهي مغناطيسية تمامًا أسفل الحقل الحرج B C (T)، وتدخل الحالة العادية غير فائقة التوصيل بمجرد تجاوز هذا الحقل. المجالات الحرجة للموصلات الفائقة من النوع الأول منخفضة جدًا بشكل عام (أقل بكثير من تسلا واحد). لهذا السبب، لا يمكن استخدامها في التطبيقات التي تتطلب إنتاج مجالات مغناطيسية عالية، والتي من شأنها تدمير حالة التوصيل الفائق.
| مادة | درجة الحرارة الحرجة (K) | المجال المغناطيسي الحرج (T) |
|---|---|---|
| النوع الأول | ||
| جميع | 1.2 | 0.011 |
| غا | 1.1 | 0.0051 |
| \(Hg(\alpha)\) | 4.2 | 0.041 |
| في | 3.4 | 0.029 |
| ملاحظة: | 9.3 | 0.20 |
| الرصاص | 7.2 | 0.080 |
| سن | 3.7 | 0.031 |
| ال | 1.4 | 0.00016 |
| ZN | 0.87 | 0.0053 |
| النوع الثاني | ||
| \(Nb_3Al\) | 18 | 32 |
| \(Nb_3Ge\) | 23 | 38 |
| \(Nb_3Sn\) | 18 | 25 |
| \(NbTi\) | 9.3 | 15 |
| \(YBa_2Cu_3O_7\) | 92 | >100 |
الموصلات الفائقة من النوع الثاني هي عمومًا مركبات أو سبائك تتضمن معادن انتقالية أو عناصر سلسلة أكتينيد. تقريبًا جميع الموصلات الفائقة ذات درجات الحرارة الحرجة المرتفعة نسبيًا هي من النوع الثاني. لديهم مجالان حاسمان، يتمثلان بـ\(B_{c1}(T)\) و\(B_{c2}(T)\). عندما يكون الحقل أدناه\(B_{c1}(T)\)، تكون الموصلات الفائقة من النوع الثاني ثنائية المغناطيسية تمامًا، ولا يمكن أن يحدث أي اختراق لتدفق مغناطيسي في المادة. في حالة تجاوز الحقل\(B_{c2}(T)\)، يتم دفعهم إلى حالتهم الطبيعية. عندما يكون المجال أكبر من\(B_{c1}(T)\) ولكن أقل من\(B_{c2}(T)\)، يُقال أن الموصلات الفائقة من النوع الثاني في حالة مختلطة. على الرغم من وجود بعض الاختراق للتدفق المغناطيسي في الحالة المختلطة، فإن مقاومة المادة تكون صفرًا. داخل الموصل الفائق، توجد مناطق تشبه الشعيرات لها خصائص كهربائية ومغناطيسية عادية تتخللها مناطق فائقة التوصيل ذات مغنطيسية مثالية. يتم تمثيل هذه الحالة في الشكل\(\PageIndex{3}\). يتم طرد المجال المغناطيسي من المناطق فائقة التوصيل ولكنه موجود في المناطق العادية. بشكل عام،\(B_{c2}(T)\) تكون كبيرة جدًا مقارنة بالمجالات الحرجة للموصلات الفائقة من النوع الأول، لذا فإن الأسلاك المصنوعة من مادة فائقة التوصيل من النوع الثاني مناسبة لفافات المغناطيس عالي المجال.
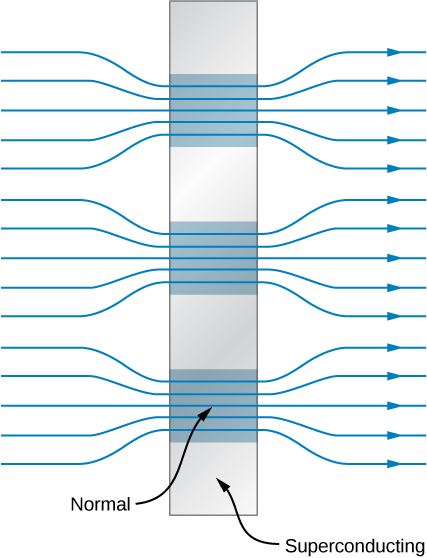
في إحدى التجارب، يُغمر سلك النيوبيوم (Nb) نصف قطره 0.25 مم في الهيليوم السائل\(T = 4.2 \, K)\) ويُطلب منه حمل تيارًا بقدرة 300 أمبير. هل يظل السلك فائق التوصيل؟
إستراتيجية
يمكن تحديد المجال المغناطيسي المطبق من نصف قطر السلك والتيار. يمكن تحديد المجال المغناطيسي الحرج من [الرابط] وخصائص الموصل الفائق ودرجة الحرارة. إذا كان المجال المغناطيسي المطبق أكبر من المجال الحرج، فسيتم تدمير الموصلية الفائقة في سلك Nb.
الحل
في\(T = 4.2 \, K\)، الحقل الحرج لـ Nb هو، من الجدول\(\PageIndex{1}\):
\[B_c(4.2 \, K) = B_c(0)\left[1 - \left(\frac{4.2 \, K}{9.3 \, K}\right)^2\right] = (0.20 \, T)(0.80) = 0.16 \, T. \nonumber \]
في فصل سابق، تعلمنا أن المجال المغناطيسي داخل سلك يحمل تيارًا نصف قطره\(a\) يُعطى بواسطة
\[B = \frac{\mu_0I}{2\pi a}, \nonumber \]
حيث r هي المسافة من المحور المركزي للسلك. وبالتالي، فإن الحقل الموجود على سطح السلك هو\(\frac{\mu_0I}{2\pi a}\). بالنسبة لسلك النيوبيوم، هذا الحقل هو
\[B = \frac{(4\pi \times 10^{-7} T m/A)(300 \, A)}{2\pi(2.5 \times 10^{-4}m)} = 0.24 \, T. \nonumber \]
نظرًا لأن هذا يتجاوز الحد الحرج البالغ 0.16 T، لا يظل السلك فائق التوصيل.
الدلالة
تتطلب الموصلية الفائقة درجات حرارة منخفضة ومجالات مغناطيسية منخفضة. يتم استيفاء هذه الشروط المتزامنة بسهولة أقل بالنسبة لـ Nb مقارنة بالعديد من المعادن الأخرى. على سبيل المثال، يتم توصيل الألمنيوم الفائق في درجات حرارة أقل بـ 7 مرات والمجالات المغناطيسية 18 مرة أقل.
ما الشروط اللازمة للموصلية الفائقة؟
- إجابة
-
درجة حرارة منخفضة ومجال مغناطيسي منخفض
نظرية الموصلات الفائقة
تم تطوير نظرية ناجحة للموصلية الفائقة في الخمسينيات من قبل جون باردين وليون كوبر وجي روبرت شريفر، وحصلوا على جائزة نوبل في عام 1972. تُعرف هذه النظرية باسم نظرية BCS. نظرية BCS معقدة، لذلك نلخصها نوعيًا أدناه.
في الموصل العادي، ترجع الخواص الكهربائية للمادة إلى الإلكترونات الأكثر نشاطًا بالقرب من طاقة فيرمي. في عام 1956، أظهر كوبر أنه إذا كان هناك أي تفاعل جذاب بين إلكترونين على مستوى فيرمي، فيمكن للإلكترونات أن تشكل حالة ملزمة تكون فيها طاقتها الإجمالية أقل من 2EF2EF. يُعرف اثنان من هذه الإلكترونات باسم زوج كوبر.
من الصعب تخيل إلكترونين يجذبان بعضهما البعض، لأن لهما شحنة متشابهة ويجب أن يصدوا. ومع ذلك، يحدث التفاعل المقترح فقط في سياق الشبكة الذرية. يظهر تصوير عامل الجذب في الشكل\(\PageIndex{4}\). يقوم الإلكترون 1 بإزاحة النوى الذرية المشحونة إيجابًا نحو نفسها قليلاً أثناء انتقالها للماضي بسبب جاذبية كولوم. «يرى» الإلكترون 2 منطقة ذات كثافة أعلى من الشحنة الموجبة بالنسبة للبيئة المحيطة، وبالتالي ينجذب إلى هذه المنطقة، وبالتالي بشكل غير مباشر، إلى الإلكترون 1. نظرًا لمبدأ الاستبعاد، يجب أن يكون للإلكترونين في زوج Cooper دوران معاكسًا.
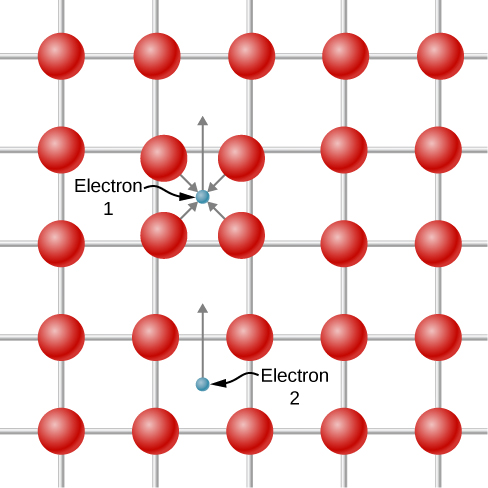
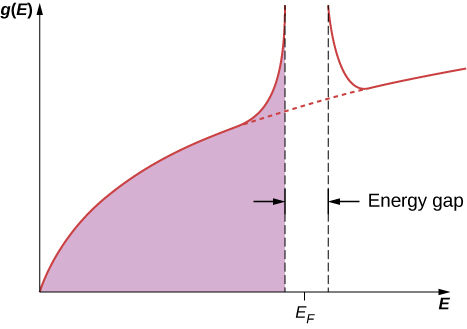
تعمل نظرية BCS على توسيع أفكار كوبر، التي تتعلق بزوج واحد من الإلكترونات، لتشمل غاز الإلكترون الحر بأكمله. عندما يحدث الانتقال إلى حالة التوصيل الفائق، تتزاوج جميع الإلكترونات لتشكل أزواج كوبر. على المقياس الذري، تكون المسافة بين الإلكترونات التي تشكل زوج Cooper كبيرة جدًا. عادةً ما تكون بين هذه الإلكترونات عبارة عن إلكترونات\(10^6\) أخرى، وتتزاوج كل منها أيضًا مع إلكترون بعيد. وبالتالي، هناك تداخل كبير بين وظائف الموجة لأزواج كوبر الفردية، مما يؤدي إلى ارتباط قوي بين حركات الأزواج. يتحركون جميعًا معًا «في خطوة»، مثل أعضاء الفرقة المسيرة. في الانتقال فائق التوصيل، تتغير كثافة الحالات بشكل جذري بالقرب من مستوى فيرمي. كما هو موضح في الشكل\(\PageIndex{5}\)، تظهر فجوة الطاقة\(E_F\) لأن مجموعة أزواج كوبر تحتوي على طاقة أرضية أقل من غاز فيرمي للإلكترونات غير المتفاعلة. يميز ظهور هذه الفجوة حالة التوصيل الفائق. إذا تم تدمير هذه الحالة، فستختفي الفجوة، وتعود كثافة الحالات إلى كثافة غاز الإلكترون الحر.
The BCS theory is able to predict many of the properties observed in superconductors. Examples include the Meissner effect, the critical temperature, the critical field, and, perhaps most importantly, the resistivity becoming zero at a critical temperature. We can think about this last phenomenon qualitatively as follows. In a normal conductor, resistivity results from the interaction of the conduction electrons with the lattice. In this interaction, the energy exchanged is on the order of \(k_BT\), the thermal energy. In a superconductor, electric current is carried by the Cooper pairs. The only way for a lattice to scatter a Cooper pair is to break it up. The destruction of one pair then destroys the collective motion of all the pairs. This destruction requires energy on the order of \(10^{-3}eV\), which is the size of the energy gap. Below the critical temperature, there is not enough thermal energy available for this process, so the Cooper pairs travel unimpeded throughout the superconductor.
Finally, it is interesting to note that no evidence of superconductivity has been found in the best normal conductors, such as copper and silver. This is not unexpected, given the BCS theory. The basis for the formation of the superconducting state is an interaction between the electrons and the lattice. In the best conductors, the electron-lattice interaction is weakest, as evident from their minimal resistivity. We might expect then that in these materials, the interaction is so weak that Cooper pairs cannot be formed, and superconductivity is therefore precluded.


