Skip to main content
Global

8.4: إلكترون سبين

  1. Last updated
  2. Save as PDF
  • Page ID
    196730

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • عبِّر عن حالة الإلكترون في ذرة الهيدروجين بدلالة خمسة أعداد كمية
    • استخدم الأرقام الكمومية لحساب حجم واتجاه الدوران والحظة المغناطيسية للإلكترون.
    • شرح البنية الدقيقة وفائقة الدقة لطيف الهيدروجين من حيث التفاعلات المغناطيسية داخل ذرة الهيدروجين

    في هذا القسم، ننظر في تأثيرات دوران الإلكترون. يقدم Spin رقمين كموميين إضافيين لنموذجنا لذرة الهيدروجين. تم اكتشاف كلاهما من خلال النظر في البنية الدقيقة للأطياف الذرية. يعد الدوران سمة أساسية لجميع الجسيمات، وليس الإلكترونات فقط، وهو مشابه للدوران الداخلي للأجسام الممتدة حول محاورها الخاصة، مثل الدوران اليومي للأرض.

    يتم قياس الدوران بنفس طريقة الزخم الزاوي المداري. لقد وجد أن حجم الزخم\(S\) الزاوي الداخلي للإلكترون يُعطى بواسطة

    \[S = \sqrt{s(s + 1)}\hbar, \nonumber \]

    حيث\(s\) يتم تعريفه على أنه الرقم الكمي للدوران. هذا مشابه للتحديد الكمي لـ\(L\)، إلا أن القيمة الوحيدة المسموح بها\(s\) للإلكترون هي\(s = 1/2\). يُقال إن الإلكترون هو «جسيم نصف الدوران». \(m_s\)يرتبط الرقم الكمي للإسقاط الدوراني بمكونات z للدوران، والتي يتم التعبير عنها بواسطة

    \[S_z = m_s\hbar. \label{eq2} \]

    بشكل عام، الأرقام الكمية المسموح بها هي

    \[m_s = -s, -s + 1, . . ., 0, . . ., +s - 1, s. \nonumber \]

    بالنسبة للحالة الخاصة للإلكترون (\(s = 1/2\))،

    \[m_s = -\frac{1}{2} \text{ or } \frac{1}{2}. \nonumber \]

    يتم تحديد اتجاهات الدوران الداخلي، تمامًا كما هو الحال بالنسبة للزخم الزاوي المداري. تسمى\(m_s = -1/2\) الحالة بحالة «الدوران» وتحتوي على مكون z أو الدوران\(s_z = -1/2\)، وتسمى\(m_s = +1/2\) الحالة الحالة «spin-up» وتحتوي على مكون z -spin،\(s_z = +1/2\). تظهر هذه الحالات في الشكل\(\PageIndex{1}\).

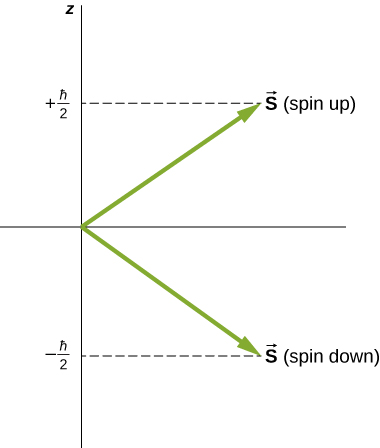
    تم توضيح حالتي الدوران المحتملتين للإلكترون كمتجهات متساوية الطول، واحدة تشير لأعلى ولليمين، وتمثل المتجه S تدور لأعلى، والأخرى تشير لأسفل ولليمين، وتمثل الدوران لأسفل. يكون المتجهان في نفس الزاوية الأفقية. يحتوي Spin up على مكون z زائد h bar على اثنين، ويحتوي spin down على مكون z أو ناقص b bar فوق 2.
    الشكل\(\PageIndex{1}\): الحالتان المحتملتان لدوران الإلكترون.

    \(\mu_e\)يمكن أيضًا التعبير عن عزم ثنائي القطب المغناطيسي الداخلي للإلكترون من حيث العدد الكمي للدوران. قياسًا على الزخم الزاوي المداري، فإن حجم العزم المغناطيسي للإلكترون هو

    \[\mu_s = \left(\frac{e}{2m_e}\right)S. \nonumber \]

    وفقًا لنظرية النسبية الخاصة، تكون هذه القيمة منخفضة بعامل 2. وهكذا، في شكل متجه، تكون اللحظة المغناطيسية للدوران

    \[\vec{\mu} = \left(\frac{e}{m_e}\right)\vec{S}. \nonumber \]

    المكون z في اللحظة المغناطيسية هو (من المعادلة\ ref {eq2})

    \[\begin{align} \mu_z &= - \left(\frac{e}{m_e}\right) S_z \\[5pt] &= - \left(\frac{e}{m_e}\right) m_s \hbar. \end{align} \nonumber \]

    يحتوي الرقم الكمي للإسقاط الدوراني على قيمتين فقط (\(m_s = \pm1/2\))، لذا فإن المكون z- في اللحظة المغناطيسية يحتوي أيضًا على قيمتين فقط:

    \[\mu_z = \pm \left(\frac{e}{2m_e}\right) = \pm \mu_B\hbar, \nonumber \]

    أين\(\mu_B\) يوجد بوهر ماغنيتون. الإلكترون مغناطيسي، لذلك نتوقع أن يتفاعل الإلكترون مع المجالات المغناطيسية الأخرى. ننظر في حالتين خاصتين: تفاعل الإلكترون الحر مع مجال مغناطيسي خارجي (غير موحد)، والإلكترون في ذرة الهيدروجين مع المجال المغناطيسي الناتج عن الزخم الزاوي المداري للإلكترون.

    إلكترون في مجال خارجي

    توفر تجربة Stern-Gerlach دليلًا تجريبيًا على أن الإلكترونات لها زخم زاوي دوراني. تمرر التجربة تيارًا من ذرات الفضة (Ag) عبر مجال مغناطيسي خارجي غير منتظم. تحتوي ذرة Ag على زخم زاوي مداري قدره صفر وتحتوي على إلكترون واحد غير مزدوج في الغلاف الخارجي. لذلك، فإن الزخم الزاوي الكلي لذرة Ag يرجع بالكامل إلى دوران الإلكترون الخارجي (\(s = 1/2\)). بسبب دوران الإلكترون، تعمل ذرات Ag كمغناطيسات صغيرة أثناء مرورها عبر المجال المغناطيسي. هذه «المغناطيسات» لها اتجاهان ممكنان، يتوافقان مع حالات الدوران لأعلى ولأسفل للإلكترون. يقوم المجال المغناطيسي بتحويل الذرات الدورانية في اتجاه واحد والذرات الدوارة في اتجاه آخر. ينتج عن هذا نطاقين متميزين على الشاشة (الشكل\(\PageIndex{2}\)).

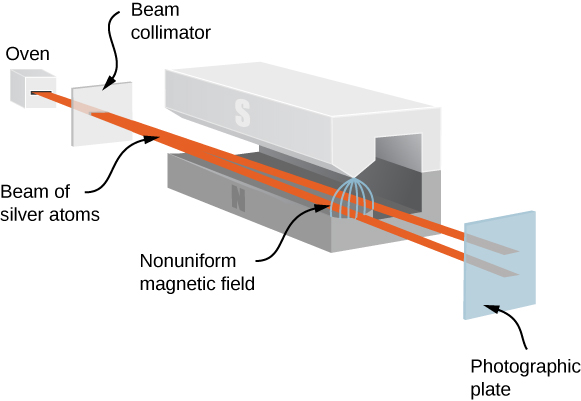
    يوضح الشكل توضيحًا لتجربة ستيرن جيرلاخ. يخرج شعاع من ذرات الفضة من الفرن ويتم موازنته أثناء مروره عبر شق. يدخل الشعاع الموازي مغناطيسًا. يؤدي المجال المغناطيسي غير المنتظم، أثناء مروره بين قطبي المغناطيس، إلى انقسام الشعاع إلى قسمين. يتحرك جزء واحد في اتجاه القطب الشمالي، والآخر في اتجاه القطب الجنوبي. يخرج الشعاعان من المغناطيس ويصطدمان بلوحة فوتوغرافية في مكانين مختلفين.
    الشكل\(\PageIndex{2}\): في تجربة Stern-Gerlach، يحوّل مجال مغناطيسي خارجي غير منتظم شعاعًا من الإلكترونات في اتجاهين مختلفين. ترجع هذه النتيجة إلى تحديد كمية الزخم الزاوي الدوراني.

    وفقًا للتنبؤات الكلاسيكية، يمكن للزخم الزاوي (وبالتالي اللحظة المغناطيسية) لذرة Ag أن يشير في أي اتجاه، لذلك يتوقع المرء، بدلاً من ذلك، تلطخًا مستمرًا على الشاشة. يوفر النطاقان الناجحان من تجربة Stern-Gerlach دعمًا مذهلاً لأفكار ميكانيكا الكم.

    قم بزيارة PhET Explorations: تجربة Stern-Gerlach لمعرفة المزيد عن تجربة Stern-Gerlach.

    مثال\(\PageIndex{1}\): Electron Spin and Radiation in An external Magnetic field

    يتم وضع ذرة الهيدروجين في الحالة الأرضية في مجال مغناطيسي خارجي موحد (\(B = 1.5 \, T\)). حدد تردد الإشعاع الناتج في الانتقال بين حالتي الدوران والانحدار للإلكترون.

    إستراتيجية

    الرقم الكمي للإسقاط الدوراني هو\(m_s = \pm 1/2\)، إذن المكون z- في اللحظة المغناطيسية هو

    \[\mu_z = \pm \left(\frac{e}{2m_e} \right) = \pm \mu_B \hbar. \nonumber \]

    الطاقة الكامنة المرتبطة بالتفاعل بين اللحظة المغناطيسية الإلكترونية والمجال المغناطيسي الخارجي هي

    \[\begin{align*} U &= - \mu_z B \\[5pt] &= \mp \mu_BB. \end{align*} \nonumber \]

    يتناسب تردد الضوء المنبعث مع فرق الطاقة (\(\Delta E\)) بين هاتين الحالتين.

    الحل

    فرق الطاقة بين هذه الحالات هو\(\Delta E = 2\mu_BB\)، وبالتالي فإن تردد الإشعاع الناتج هو

    \[\begin{align*} f = \dfrac{\Delta E}{h} &= \frac{2\mu_BB}{h} \\[5pt] &= \frac{2\left(5.79 \times \frac{10^{-5} eV}{T}\right)(1.5 \, T)}{4.136 \times 10^{-15} eV \cdot s} \\[5pt] &= 4.2 \times 10^{10} \, \frac{cycles}{s}. \end{align*} \nonumber \]

    الدلالة

    تتزاوج اللحظة المغناطيسية الإلكترونية مع المجال المغناطيسي الخارجي. تختلف طاقة هذا النظام سواء كان الإلكترون محاذيًا للبروتون أم لا. يتناسب تردد الإشعاع الناتج عن الانتقال بين هذه الحالات مع فرق الطاقة. إذا ضاعفنا قوة المجال المغناطيسي، مع إبقاء جميع الأشياء الأخرى ثابتة، يتضاعف تردد الإشعاع ويخفض طوله الموجي إلى النصف.

    التمارين\(\PageIndex{1}\)

    إذا أسفرت تجربة Stern-Gerlach عن أربعة نطاقات متميزة بدلاً من نطاقين، فما الذي يمكن استنتاجه بشأن العدد الكمي للدوران للجسيم المشحون؟

    إجابة

    \(s = 3/2 <\)

    اقتران الدوران والمدار (الهيكل الدقيق)

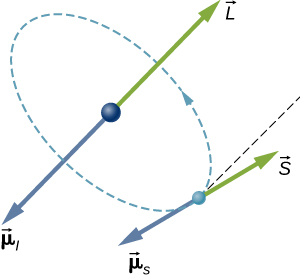
    في ذرة الهيدروجين، يمكن أن تتفاعل اللحظة المغناطيسية للإلكترون مع المجال المغناطيسي الناتج عن الزخم الزاوي المداري للإلكترون، وهي ظاهرة تسمى اقتران الدوران والمدار. يتم عرض متجه الزخم الزاوي المداري (\(\vec{\mu}\)) والعزم المغناطيسي المداري (\(\vec{S}\)) والزخم الزاوي الدوراني (\(\vec{\mu}_s\)) والزخم الزاوي للدوران () معًا في الشكل\(\PageIndex{3}\).\(\vec{L}\)

    مثلما يمكن تقسيم مستويات الطاقة لذرة الهيدروجين بواسطة مجال مغناطيسي خارجي، كذلك يتم تقسيم مستويات الطاقة لذرة الهيدروجين بواسطة المجالات المغناطيسية الداخلية للذرة. إذا كانت اللحظة المغناطيسية للإلكترون والحظة المغناطيسية المدارية للإلكترون مضادة للتوازي، فإن الطاقة الكامنة من التفاعل المغناطيسي تكون عالية نسبيًا، ولكن عندما تكون هذه اللحظات متوازية، تكون الطاقة الكامنة صغيرة نسبيًا. يؤدي الانتقال من كل من هاتين الحالتين إلى مستوى طاقة أقل إلى انبعاث فوتون بتردد مختلف قليلاً. أي أن اقتران المدار الدوراني «يقسم» الخط الطيفي المتوقع من إلكترون بدون دوران. يتم تفسير البنية الدقيقة للطيف الهيدروجيني من خلال اقتران الدوران والمدار.

    يُوضَّح مدار الإلكترون في الذرة على هيئة كرة صغيرة في مدار دائري حول كرة أكبر في مركز الدائرة. يتم تحديد اتجاه السفر باليد اليمنى (حسب عقارب الساعة عند النظر إليها.) في النواة، يشير المتجه L إلى الأعلى (مرة أخرى، كما هو موضح من الأعلى) ويشير المتجه mu sub l إلى الأسفل. عند الإلكترون، يشير متجه S إلى زاوية غير محددة بالنسبة لاتجاه L، ويشير متجه mu subs s في الاتجاه المعاكس لـ S.
    الشكل\(\PageIndex{3}\): اقتران الدوران في المدار هو تفاعل اللحظة المغناطيسية الدوارة للإلكترون\(\vec{mu}_s\) مع لحظته المغناطيسية المدارية\(\vec{\mu}_l\).

    اقتران الدوران النووي للإلكترون (هيكل فائق الدقة)

    تمامًا مثل الإلكترون، يدور البروتون بمقدار 1/2 وله لحظة مغناطيسية. (وفقًا للنظرية النووية، ترجع هذه اللحظة إلى الحركة المدارية للكواركات داخل البروتون.) يتم تفسير البنية فائقة الدقة لطيف الهيدروجين من خلال التفاعل بين اللحظة المغناطيسية للبروتون والحظة المغناطيسية للإلكترون، وهو تفاعل يعرف باسم اقتران الدوران. تختلف طاقة نظام البروتون الإلكتروني اعتمادًا على ما إذا كانت اللحظات محاذاة أم لا. تؤدي التحولات بين هذه الحالات (التحولات الدورانية) إلى انبعاث فوتون بطول موجة\(\lambda = 21\) سم (في نطاق الراديو). الخط البالغ 21 سم في التحليل الطيفي الذري هو «بصمة» لغاز الهيدروجين. يستغل علماء الفلك هذا الخط الطيفي لرسم خريطة للأذرع الحلزونية للمجرات، والتي تتكون في الغالب من الهيدروجين (الشكل\(\PageIndex{4}\)).

    ثلاث صور تلسكوبية لمجرة دولاب الدوران. في الشكل أ، تظهر الصورة بالضوء المرئي. تظهر المجرة كمجموعة من النجوم، كثيفة جدًا في الوسط وذات أذرع متصاعدة. الشكل (ب) هو صورة إشعاعية بطول 21 سم. تكون الطبيعة الحلزونية أكثر وضوحًا في هذه الصورة، والانتفاخ المركزي غائب. يغطي الشكل c كلاً من الصور المرئية والصور التي يبلغ طولها 21 سم.
    الشكل\(\PageIndex{4}\): يتم استخدام التفاعل المغناطيسي بين الإلكترون والبروتون في ذرة الهيدروجين لرسم خريطة للأذرع الحلزونية لمجرة دولاب (NGC 5457). (أ) المجرة التي تُرى في الضوء المرئي؛ (ب) المجرة التي تُرى في إشعاع هيدروجيني طوله 21 سم؛ (ج) الصورة المركبة لـ (أ) و (ب). لاحظ كيف يخترق انبعاث الهيدروجين الغبار في المجرة لإظهار الأذرع الحلزونية بوضوح شديد، بينما تظهر نواة المجرة بشكل أفضل في الضوء المرئي (الفضل أ: تعديل العمل من قبل وكالة الفضاء الأوروبية ووكالة ناسا؛ الفضل ب: تعديل عمل فابيان والتر).

    تتطلب المواصفات الكاملة لحالة الإلكترون في ذرة الهيدروجين خمسة أرقام كمية: n، l، m، s، و\(m_s\). يتم تلخيص الأسماء والرموز والقيم المسموح بها لهذه الأرقام الكمومية في الجدول\(\PageIndex{4}\).

    جدول\(\PageIndex{4}\): ملخص الأعداد الكمومية للإلكترون في ذرة الهيدروجين
    اسم الرمز القيم المسموح بها
    الرقم الكمي الرئيسي ن 1، 2، 3،...
    الزخم الزاوي ل 0، 1، 2،... ن — 1
    إسقاط الزخم الزاوي م \(0, \pm 1, \pm 2, . . . \pm l\)
    سبين ثانية 1/2 (إلكترونات)
    إسقاط الدوران \(m_s\) \(- 1/2, \, +1/2\)

    لاحظ أن الأرقام الكمومية الجوهرية المقدمة في هذا القسم (\(s\)و\(m_s\)) صالحة للعديد من الجسيمات، وليس فقط الإلكترونات. على سبيل المثال، الكواركات داخل النواة الذرية هي أيضًا جزيئات نصف دوارة. كما سنرى لاحقًا، تساعد الأرقام الكمومية في تصنيف الجسيمات دون الذرية والدخول في نماذج علمية تحاول شرح كيفية عمل الكون.