Skip to main content
Global

8.5: مبدأ الاستبعاد والجدول الدوري

  1. Last updated
  2. Save as PDF
  • Page ID
    196724

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • شرح أهمية مبدأ استبعاد باولي لفهم التركيب الذري والترابط الجزيئي
    • اشرح بنية الجدول الدوري بدلالة الطاقة الكلية والزخم الزاوي المداري ودوران الإلكترونات الفردية في الذرة
    • وصف التكوين الإلكتروني للذرات في الجدول الدوري

    حتى الآن، درسنا الهيدروجين فقط، أبسط عنصر كيميائي. لقد وجدنا أن الإلكترون في ذرة الهيدروجين يمكن تحديده بالكامل بخمسة أرقام كمية:

    • \(n\):رقم الكم الرئيسي
    • \(l\): العدد الكمي للزخم الزاوي
    • \(m\): الرقم الكمي لإسقاط الزخم الزاوي
    • \(s\): رقم الكم المغزلي
    • \(m_s\): الرقم الكمي للإسقاط الدوراني

    لتكوين الحالة الأرضية لذرة محايدة متعددة الإلكترون، تخيل البدء بنواة الشحنة Ze (أي نواة العدد الذري Z) ثم إضافة الإلكترونات Z واحدة تلو الأخرى. افترض أن كل إلكترون يتحرك في مجال كهربائي متماثل كرويًا تنتجه النواة وجميع إلكترونات الذرة الأخرى. هذا الافتراض صحيح لأن الإلكترونات يتم توزيعها عشوائيًا حول النواة وتنتج مجالًا كهربائيًا متوسطًا (وإمكانًا) متماثلًا كرويًا. لا يتبع الجهد الكهربائي U (r) لكل إلكترون\(-1/r\) الشكل البسيط بسبب التفاعلات بين الإلكترونات، ولكن اتضح أنه لا يزال بإمكاننا تسمية كل حالة إلكترون فردية بالأرقام الكمومية، (\(n,l,m,s,m_s\)). (الرقم الكمي للدوران\(s\) هو نفسه لجميع الإلكترونات، لذلك لن يتم استخدامه في هذا القسم.)

    يتم شرح البنية والخصائص الكيميائية للذرات جزئيًا من خلال مبدأ استبعاد باولي: لا يمكن أن يكون لإلكترونين في الذرة نفس القيم لجميع الأرقام الكمومية الأربعة (\(n,l,m,m_s\)). يرتبط هذا المبدأ بخاصيتين للإلكترونات: جميع الإلكترونات متطابقة («عندما ترى إلكترونًا واحدًا، تكون قد رأيتهم جميعًا») ولها دوران نصف متكامل (\(s = 1/2\)). يتم إعطاء مجموعات عينات من الأرقام الكمومية للإلكترونات في الذرة في الجدول\(\PageIndex{1}\). وفقًا لمبدأ استبعاد باولي، لا يوجد صفان من الجدول لهما نفس مجموعة الأرقام الكمومية بالضبط.

    الجدول\(\PageIndex{1}\): الحالات الإلكترونية للذرات بسبب مبدأ استبعاد باولي، لا يوجد إلكترونان في الذرة لهما نفس المجموعة المكونة من أربعة أرقام كمية.
    \(n\) \(l\) \(m\) \(m_s\) رمز subshell عدد الإلكترونات: القشرة الفرعية عدد الإلكترونات: القشرة
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m_s\)» النمط = «المحاذاة الرأسية: الوسطى؛" >½ 1 ثانية 2 2
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m_s\)» النمط = «محاذاة رأسية: متوسطة؛" >—½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m_s\)» النمط = «المحاذاة الرأسية: الوسطى؛" >½ 2 ثانية 2 8
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m_s\)» النمط = «محاذاة رأسية: متوسطة؛" >—½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >—1 \ (m_s\)» النمط = «المحاذاة الرأسية: الوسطى؛" >½ 2 ص 6
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >—1 \ (m_s\)» النمط = «محاذاة رأسية: متوسطة؛" >—½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m_s\)» النمط = «المحاذاة الرأسية: الوسطى؛" >½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m_s\)» النمط = «محاذاة رأسية: متوسطة؛" >—½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m\)» النمط = «المحاذاة الرأسية: متوسطة؛" >1 \ (m_s\)» النمط = «المحاذاة الرأسية: الوسطى؛" >½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m\)» النمط = «المحاذاة الرأسية: متوسطة؛" >1 \ (m_s\)» النمط = «محاذاة رأسية: متوسطة؛" >—½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m_s\)» النمط = «المحاذاة الرأسية: الوسطى؛" >½ 3 ثانية 2 18
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m_s\)» النمط = «محاذاة رأسية: متوسطة؛" >—½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >—1 \ (m_s\)» النمط = «المحاذاة الرأسية: الوسطى؛" >½ 3 ص 6
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >—1 \ (m_s\)» النمط = «محاذاة رأسية: متوسطة؛" >—½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m_s\)» النمط = «المحاذاة الرأسية: الوسطى؛" >½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m_s\)» النمط = «محاذاة رأسية: متوسطة؛" >—½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m_s\)» النمط = «المحاذاة الرأسية: الوسطى؛" >½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m_s\)» النمط = «محاذاة رأسية: متوسطة؛" >—½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >—2 \ (m_s\)» النمط = «المحاذاة الرأسية: الوسطى؛" >½ 3 د 10
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >—2 \ (m_s\)» النمط = «محاذاة رأسية: متوسطة؛" >—½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >—1 \ (m_s\)» النمط = «المحاذاة الرأسية: الوسطى؛" >½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >—1 \ (m_s\)» النمط = «محاذاة رأسية: متوسطة؛" >—½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m_s\)» النمط = «المحاذاة الرأسية: الوسطى؛" >½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >0 \ (m_s\)» النمط = «محاذاة رأسية: متوسطة؛" >—½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m_s\)» النمط = «المحاذاة الرأسية: الوسطى؛" >½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >1 \ (m_s\)» النمط = «محاذاة رأسية: متوسطة؛" >—½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (m_s\)» النمط = «المحاذاة الرأسية: الوسطى؛" >½
    \ (n\)» النمط = «محاذاة رأسية: متوسطة؛" >3 \ (l\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (m\)» النمط = «محاذاة رأسية: متوسطة؛" >2 \ (m_s\)» النمط = «محاذاة رأسية: متوسطة؛" >—½

    يُقال إن الإلكترونات التي لها نفس العدد الكمي الرئيسي n موجودة في نفس الغلاف، ويقال أن تلك التي لها نفس قيمة l تحتل نفس الغلاف الفرعي. يُشار إلى الإلكترون في\(n = 1\) حالة ذرة الهيدروجين بـ 1 ثانية، حيث يشير الرقم الأول إلى الغلاف (\(n = 1\)) ويشير الحرف إلى الغلاف الفرعي (\(s,p,d,f,...\)يتوافق مع\(l = 0,1,2,3,...\)). يُشار إلى إلكترونين في\(n = 1\) الحالة على\(1s^2\) أنهما، حيث يشير الخط العلوي إلى عدد الإلكترونات. يُشار إلى الإلكترون في\(n = 2\) الحالة\(l = 1\) بـ 2 p. تتم كتابة تركيبة إلكترونين في\(n = 2\)\(l = 0\) الحالة n، وثلاثة إلكترونات في\(l = 1\) الحالة AND كـ\(2s^22p^3\)، وهكذا.\(n = 2\) هذا التمثيل لحالة الإلكترون يسمى التكوين الإلكتروني للذرة. ترد التكوينات الإلكترونية للعديد من الذرات في الجدول\(\PageIndex{2}\). تسمى الإلكترونات الموجودة في الغلاف الخارجي للذرة بإلكترونات التكافؤ. يتم تفسير الترابط الكيميائي بين الذرات في الجزيء من خلال نقل وتقاسم إلكترونات التكافؤ.

    الجدول\(\PageIndex{2}\): التكوينات الإلكترونية للإلكترونات في الذرة. يشير الرمز (↑) إلى إلكترون غير مزدوج في الغلاف الخارجي، بينما يشير الرمز (↑ ↓) إلى زوج من الإلكترونات الدوارة والهابطة في الغلاف الخارجي.
    العنصر تكوين الإلكترون محاذاة الدوران
    ح \(1s^1\) (↑)
    هو \(1s^2\) (↑ ↓)
    لي \(1s^22s^1\) (↑)
    كن \(1s^22s^2\) (↑ ↓)
    ب \(1s^22s^22p^1\) (↑ ↓) (↑)
    ج \(1s^22s^22p^2\) (↑ ↓) (↑) (↑)
    ن \(1s^22s^22p^3\) (↑ ↓) (↑) (↑) (↑)
    O \(1s^22s^22p^4\) (↑ ↓) (↑ ↓) (↑) (↑)
    و \(1s^22s^22p^5\) (↑ ↓) (↑ ↓) (↑ ↓) (↑)
    جديد \(1s^22s^22p^6\) (↑ ↓) (↑ ↓) (↑ ↓) (↑ ↓)
    نا \(1s^22s^22p^63s^1\) (↑)
    ملغ \(1s^22s^22p^63s^2\) (↑ ↓)
    جميع \(1s^22s^22p^63s^13p^1\) (↑ ↓) (↑)

    يعتمد الحد الأقصى لعدد الإلكترونات في الغلاف الفرعي على قيمة الرقم الكمي للزخم الزاوي، l. بالنسبة لقيمة معينة l، توجد حالات زخم زاوي\(2l + 1\) مداري. ومع ذلك، يمكن ملء كل حالة من هذه الحالات بإلكترونين (الدوران لأعلى ولأسفل، ↑ ↓). وبالتالي، فإن الحد الأقصى لعدد الإلكترونات في الغلاف الفرعي هو

    \[N = 2(2l + 1) = 4l + 2. \nonumber \]

    في الغلاف الفرعي 2 s (\(l = 0\))، يكون الحد الأقصى لعدد الإلكترونات هو 2. في الغلاف الفرعي 2 p (\(l = 1\))، يكون الحد الأقصى لعدد الإلكترونات هو 6. لذلك، يكون الحد الأقصى الإجمالي لعدد الإلكترونات في\(n = 2\) الغلاف (بما في ذلك كل من الأصداف الفرعية\(l = 0\) و 1)\(2 + 6\) هو 8. بشكل عام، الحد الأقصى لعدد الإلكترونات في الغلاف n هو\(2n^2\).

    مثال\(\PageIndex{1}\): Subshells and Totals for \(n = 3\)

    كم عدد الأصداف الفرعية الموجودة في\(n = 3\) القشرة؟ حدد كل غلاف فرعي واحسب الحد الأقصى لعدد الإلكترونات التي ستملأ كل منها. أظهر أن الحد الأقصى لعدد الإلكترونات التي تملأ الذرة هو\(2n^2\).

    إستراتيجية

    يتم تحديد الأصداف الفرعية بقيمة l؛ وبالتالي، نحدد أولاً قيم l المسموح بها، ثم نطبق معادلة «الحد الأقصى لعدد الإلكترونات التي يمكن أن تكون في a\(subshell = 2(2l + 1\))» للعثور على عدد الإلكترونات في كل قشرة فرعية.

    الحل

    لأننا\(n = 3\) نعلم أن l يمكن أن يكون 0 أو 1 أو 2؛ وبالتالي، هناك ثلاث قذائف فرعية محتملة. في الترميز القياسي، يتم تسميتها بالقشور الفرعية 3 s و 3 p و 3 d. لقد رأينا بالفعل أن إلكترونين يمكن أن يكونا في حالة s، وستة في حالة p، ولكن دعونا نستخدم معادلة «الحد الأقصى لعدد الإلكترونات التي يمكن أن تكون في

    subshell\(= 2(2l + 1)\)» لحساب الحد الأقصى للرقم في كل منها:

    \(3s\)لديه\(l = 0\)؛ وبالتالي،\(2(2l + 1) = 2(0 + 1) = 2\)

    \(3p\)لديه\(l = 1\)؛ وبالتالي،\(2(2l + 1) = 2(2 + 1) = 6\)

    \(3d\)لديه\(l = 2\)؛ وبالتالي،\(2(2l + 1) = 2(4 + 1) = 10\)

    \(Total = 18\)

    (في\(n = 3\) القشرة).

    تعطي المعادلة «الحد الأقصى لعدد الإلكترونات التي يمكن أن تكون في الغلاف =\(2n^2\)» الحد الأقصى لعدد الإلكترونات في\(n = 3\) الغلاف

    الحد الأقصى لعدد الإلكترونات\(= 2n^2 = 2(3)^2 = 2(9) = 18\).

    الدلالة

    وبالتالي فإن العدد الإجمالي للإلكترونات في الأصداف الفرعية الثلاثة المحتملة هو نفس الصيغة\(2n^2\). في الترميز القياسي (الطيفي)، يُشار إلى\(n = 3\) الغلاف المملوء كـ\(3s^23p^63d^{10}\). لا تملأ الأصداف بطريقة بسيطة. قبل ملء\(n = 3\) الغلاف بالكامل، على سبيل المثال، نبدأ في العثور على الإلكترونات في\(n = 4\) الغلاف.

    يمكن فهم بنية الجدول الدوري (الشكل\(\PageIndex{1}\)) من حيث الأصداف والأصداف الفرعية، وفي النهاية، الطاقة الكلية والزخم الزاوي المداري ودوران الإلكترونات في الذرة. تُترك المناقشة التفصيلية للجدول الدوري لدورة الكيمياء - نرسم فقط ميزاته الأساسية هنا. في هذه المناقشة، نفترض أن الذرات محايدة كهربائيًا؛ أي أنها تحتوي على نفس عدد الإلكترونات والبروتونات. (تذكر أن العدد الإجمالي للبروتونات في نواة الذرة يسمى العدد الذري، Z.)

    أولاً، يتم ترتيب الجدول الدوري في أعمدة وصفوف. تتم قراءة الجدول من اليسار إلى اليمين ومن أعلى إلى أسفل بترتيب زيادة العدد الذري\(Z\). تشترك الذرات التي تنتمي إلى نفس العمود أو المجموعة الكيميائية في العديد من الخصائص الكيميائية نفسها. على سبيل المثال، ترتبط ذرات Li و Na (في العمود الأول) بالذرات الأخرى بطريقة مماثلة. يتوافق الصف الأول من الجدول مع غلاف 1 s (\(l = 0\)) للذرة.

    ضع في اعتبارك الإجراء الافتراضي لإضافة الإلكترونات، واحدة تلو الأخرى، إلى الذرة. بالنسبة للهيدروجين (H) (أعلى اليسار)، يتم ملء غلاف 1 ثانية بإلكترون يدور لأعلى أو لأسفل (↑ أو ↓). يتم مشاركة هذا الإلكترون الوحيد بسهولة مع الذرات الأخرى، لذا فإن الهيدروجين نشط كيميائيًا. بالنسبة للهيليوم (He) (الجزء العلوي الأيمن)، يتم ملء غلاف 1 s بكل من الإلكترون الذي يدور لأعلى ويدور لأسفل (↑ ↓). هذا «يملأ» غلاف 1 s، لذلك تميل ذرة الهيليوم إلى عدم مشاركة الإلكترونات مع الذرات الأخرى. يُقال إن ذرة الهيليوم غير نشطة كيميائيًا أو خاملة أو نبيلة؛ وبالمثل، يُقال إن غاز الهيليوم هو غاز خامل أو غاز نبيل.

    قم ببناء ذرة عن طريق إضافة وطرح البروتونات والنيوترونات والإلكترونات. كيف يتغير العنصر والشحنة والكتلة؟ قم بزيارة PhET Explorations: قم ببناء ذرة لاستكشاف إجابات هذه الأسئلة.

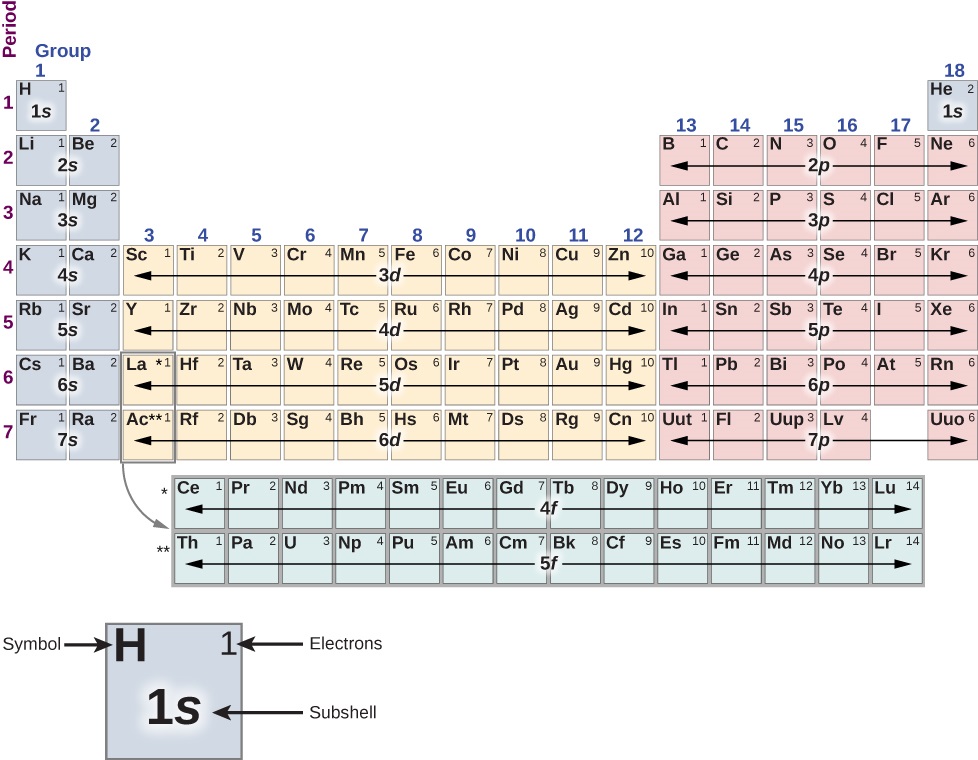
    يظهر الجدول الدوري للعناصر، الذي يُظهر بنية الأصداف والأصداف الفرعية. تم ترقيم الأعمدة الثمانية عشر باسم «المجموعة» ويتم ترقيم الصفوف السبعة وتسميتها «الفترة». المجموعتان 1 و 2 مظللة باللون الأرجواني. المجموعات من 3 إلى 12 مظللة باللون الأصفر. المجموعات من 13 إلى 18 مظللة باللون الأحمر، باستثناء الفترة 1، المجموعة 18، وهي باللون الأرجواني. تم تحديد مربعات الفترة 6 و 7 والمجموعة 3 ويشير السهم منها إلى قسم إضافي من صفين و 14 عمودًا مظللًا باللون الأخضر. يحتوي مربع الفترة 6 group 3 على علامة النجمة، والتي تظهر أيضًا على يسار الصف الأول من القسم الإضافي. يحتوي مربع المجموعة 3 للفترة 7 على علامتين نجمتين تظهران أيضًا على يسار الصف الثاني من القسم الإضافي. أسفل الجدول على اليسار توجد صورة مكبرة للمربع العلوي الأيسر على الطاولة. يوجد الحرف «H» في الزاوية العلوية اليسرى ويسمى «الرمز». الرقم 1 موجود في الزاوية العلوية اليمنى ويحمل اسم «الإلكترونات». يُطلق على الإدخال «1 s» في وسطه اسم «subshell». الصندوق مظلل باللون الأرجواني. كل عنصر له رمزه والإلكترونات المشار إليها في المربع. يشار إلى الأصداف الفرعية كمجموعة للأقسام المتجاورة من الصف. بدءًا من أعلى يسار الجدول، تظهر الفترة 1، المجموعة 1، باللون الأرجواني وتحتوي على الرمز H، والإلكترونات 1، والقشرة الفرعية 1 ثانية، بينما يوجد مربع العناصر الآخر الوحيد في الفترة 1 في العمود الأخير، المجموعة 18، وهو مظلل باللون الأرجواني ويحتوي على «H e، 1، 1 s». الفترة 2، المجموعة 1 تحتوي على «L i، 1" المجموعة 2 تحتوي على «B e، 2". تحتوي كل من مجموعتي الفترة 2 1 و 2 على هيكل فرعي 2 ثانية. يتم تخطي المجموعات من 3 إلى 12. تحتوي المجموعة 13 على «B، 1". تحتوي المجموعة 14 على «C، 2". تحتوي المجموعة 15 على «N، 3". تحتوي المجموعة 16 على «O، 4". تحتوي المجموعة 17 على «F، 5". تحتوي المجموعة 18 على «N e، 6". تحتوي المجموعة الثانية من 13 إلى 18 على الجزء الفرعي 2 ص، الفترة 3، المجموعة 1 تحتوي على «N a.1». تحتوي المجموعة 2 على «M g، 2". يحتوي هذان العنصران على عنوان فرعي 3 ثوانٍ، ويتم تخطي المجموعات من 3 إلى 12 مرة أخرى في الفترة 3 وتحتوي المجموعة 13 على «A l، 1». تحتوي المجموعة 14 على «S I، 2". تحتوي المجموعة 15 على «P، 3". تحتوي المجموعة 16 على «S، 4". تحتوي المجموعة 17 على «C l، 5". تحتوي المجموعة 18 على «A r، 6". تحتوي هذه الستة على غلاف فرعي 3 ص. الفترة 4، المجموعة 1 تحتوي على «K، 1.» تحتوي المجموعة 2 على «C a، 2". يحتوي هذان الشخصان على القسم الفرعي 4 s. المجموعة 3 تحتوي على «S، 1.» تحتوي المجموعة 4 على «T i، 2". تحتوي المجموعة 5 على «V، 3". تحتوي المجموعة 6 على «C r، 4". تحتوي المجموعة 7 على «M n، 5". تحتوي المجموعة 8 على «F e، 6". تحتوي المجموعة 9 على «C o، 7". تحتوي المجموعة 10 على «N i، 8". تحتوي المجموعة 11 على «C u، 9". تحتوي المجموعة 12 على «Z n، 10". تحتوي هذه الـ 10 على عنوان فرعي 3 د. تحتوي المجموعة 13 على «G a، 1". تحتوي المجموعة 14 على «G e، 2". تحتوي المجموعة 15 على «A s، 3.» تحتوي المجموعة 16 على «S e، 4". تحتوي المجموعة 17 على «B r، 5". تحتوي المجموعة 18 على «K r، 6". هذه الستة لها غلاف فرعي 4 ص. الفترة 5، المجموعة 1 تحتوي على «R b، 1.» تحتوي المجموعة 2 على «S r، 2". تحتوي هاتان الوثيقتان على عنوان فرعي 5 s. تحتوي المجموعة 3 على «Y، 1". تحتوي المجموعة 4 على «Z r، 2". تحتوي المجموعة 5 على «N b، 3". تحتوي المجموعة 6 على «M o، 4". تحتوي المجموعة 7 على «T c، 5 «R u، 6". تحتوي المجموعة 9 على «R h، 7". تحتوي المجموعة 10 على «P d، 8". تحتوي المجموعة 11 على «A g، 9". تحتوي المجموعة 12 على «C d، 10". تحتوي هذه العشرة على القسم الفرعي 4 د. المجموعة 13 تحتوي على «I n، 1". تحتوي المجموعة 14 على «S n، 2". تحتوي المجموعة 15 على «S b، 3". تحتوي المجموعة 16 على «T e، 4". تحتوي المجموعة 17 على «أنا، 5.» تحتوي المجموعة 18 على «X e، 6". هذه الستة لها غلاف فرعي 5 ص. الفترة 6، المجموعة 1 تحتوي على «C s، 1.» تحتوي المجموعة 2 على «B a، 2". يحتوي هذان العنصران على القسم الفرعي 6 s. تحتوي المجموعة 3 على «L a، 1"، ولها علامة نجمية إضافية. تحتوي المجموعة 4 على «H f، 2". تحتوي المجموعة 5 على «T a، 3". تحتوي المجموعة 6 على «W، 4". تحتوي المجموعة 7 على «R e، 5". تحتوي المجموعة 8 على «O s، 6". تحتوي المجموعة 9 على «I r، 7". تحتوي المجموعة 10 على «P t، 8". تحتوي المجموعة 11 على «A u، 9". تحتوي المجموعة 12 على «H g، 10". تحتوي هذه 10 على عنوان فرعي 5 د. تحتوي المجموعة 13 على «T l، 1.» تحتوي المجموعة 14 على «P b، 2". تحتوي المجموعة 15 على «B i، 3". تحتوي المجموعة 16 على «P o، 4". تحتوي المجموعة 17 على «A t، 5". تحتوي المجموعة 18 على «R n، 6". هذه الستة لها غلاف فرعي 6 ص. الفترة 7، المجموعة 1 تحتوي على «F r، 1.» تحتوي المجموعة 2 على «R a، 2". يحتوي هذان العنصران على القسم الفرعي 7 s. تحتوي المجموعة 3 على «A c، 1" ولها علامة نجمية مزدوجة إضافية. تحتوي المجموعة 4 على «R f، 2". تحتوي المجموعة 5 على «D b، 3". تحتوي المجموعة 6 على «S g، 4". تحتوي المجموعة 7 على «B h، 5". تحتوي المجموعة 8 على «H s، 6". تحتوي المجموعة 9 على «M t، 7". تحتوي المجموعة 10 على «D s، 8". تحتوي المجموعة 11 على «R g، 9". تحتوي المجموعة 12 على «C n، 10". تحتوي هذه 10 على عنوان فرعي 6 د. تحتوي المجموعة 13 على «U u t, 1.» تحتوي المجموعة 14 على «F l، 2". تحتوي المجموعة 15 على «U up, 3". تحتوي المجموعة 16 على «L v، 4". المجموعة 17 مفقودة. تحتوي المجموعة 18 على «U up o, 6". تحتوي هذه الخمسة على هيكل فرعي 7 ص. يربط السهم الفترة 6 و 7، المجموعة 3 بقسم إضافي به صفين، كل منهما يحتوي على 14 عمودًا. لا يتم ترقيم الأعمدة. يُصنف الصف الأول بعلامة النجمة وجميع العناصر فيه تحتوي على الغلاف الفرعي 4 f، وتحتوي المربعات الموجودة في هذا الصف، بالترتيب: C e، 1، P r، 2، N d، 3، P m، 4، S m، 5، E u، 6، G d، 7، T b، 8، D y، 9، H o، 10، E r، 11، T m، 12، Y b، 13، إل جو، 14. يُصنف الصف الثاني بعلامة نجمية مزدوجة وتحتوي جميع العناصر الموجودة فيه على الغلاف الفرعي 5 f، وتحتوي المربعات الموجودة في هذا الصف، بالترتيب: T h 1، P a، 2، U، 3، N p، 4، P u، 5، A m، 6، C m، 7، B k، 8، C f، 9، E s، 10، F m، 11، M d، 12، N o، 13، L أو 14.
    الشكل\(\PageIndex{1}\): الجدول الدوري للعناصر، يوضح بنية الأصداف والأصداف الفرعية.

    يتوافق الصف الثاني مع الأصداف الفرعية 2 ثانية و 2 p. بالنسبة إلى الليثيوم (Li) (الجزء العلوي الأيسر)، يتم ملء غلاف 1 ثانية بإلكترون يدور لأعلى ولأسفل (↑ ↓) ويتم ملء غلاف 2 ثانية إما بإلكترون دوار أو لأسفل (↑ أو ↓). وبالتالي فإن تكوينه الإلكتروني هو\(1s^22s^1\) أو [He] 2 s، حيث يشير [He] إلى نواة الهيليوم. مثل الهيدروجين، يتم مشاركة الإلكترون الوحيد الموجود في الغلاف الخارجي بسهولة مع الذرات الأخرى. بالنسبة للبيريليوم (Be)، يتم ملء غلاف 2 s بإلكترون يدور لأعلى ولأسفل (↑ ↓)، وله تكوين الإلكترون [He]\(2s^2\).

    بعد ذلك، ننظر إلى الجانب الأيمن من الجدول. بالنسبة للبورون (B)، يتم ملء قذائف 1 ثانية و 2 ثانية وتحتوي قشرة 2 p (\(l = 1\)) إما على إلكترون يدور لأعلى أو لأسفل (↑ أو ↓). من الكربون (C) إلى النيون (N)، نقوم بعد ذلك بملء الغلاف المكون من 2 p. الحد الأقصى لعدد الإلكترونات في قذائف 2 p هو\(4l + 2 = 4(2) + 2 = 6\). بالنسبة للنيون (Ne)، يتم ملء غلاف 1 ثانية بإلكترون يدور لأعلى ولأسفل (↑ ↓)، ويتم ملء الغلاف المكون من 2 p بستة إلكترونات (↑ ↓). هذا «يملأ» الأصداف الفرعية 1 s و 2 s و 2 p، لذلك مثل الهيليوم، تميل ذرة النيون إلى عدم مشاركة الإلكترونات مع الذرات الأخرى.

    تتكرر عملية تعبئة الإلكترون في الصف الثالث. ومع ذلك، بدءًا من الصف الرابع، يتم كسر النمط. يتم إعطاء الترتيب الفعلي لترتيب تعبئة الإلكترون بواسطة

    1 ثانية، 2 ثانية، 2 ص، 3 ثوان، 3 ص، 4 ثانية، 3 د، 4 ص، 5 ثانية، 4 د، 5 ص، 6 ثانية، 4 فهرنهايت، 5 د، 6 ص، 7 ثانية،...

    لاحظ أن الأصداف الفرعية 3 d و 4 d و 4 f و 5 d (بالخط العريض) مملوءة خارج الترتيب؛ يحدث هذا بسبب التفاعلات بين الإلكترونات في الذرة، والتي أهملناها حتى الآن. المعادن الانتقالية هي عناصر في الفجوة بين العمودين الأولين والأعمدة الستة الأخيرة التي تحتوي على الإلكترونات التي تملأ الغلاف الفرعي d (\(l = 1\)). كما هو متوقع، يتم ترتيب هذه الذرات في\(4l + 2 = 4(2) + 2 = 10\) أعمدة. يمكن فهم بنية الجدول الدوري من حيث تحديد كمية الطاقة الكلية (n) والزخم الزاوي المداري (l) والدوران (s). يتوافق العمودان الأولان مع الهيكل الفرعي s (\(l = 0\))، وتتوافق الأعمدة الستة التالية مع الهيكل الفرعي p (\(l = 1\))، وتتوافق الفجوة بين هذه الأعمدة مع الهيكل الفرعي d (\(l = 2\)).

    يقدم الجدول الدوري أيضًا معلومات عن الترابط الجزيئي. لرؤية ذلك، ضع في اعتبارك الذرات الموجودة في العمود الموجود في أقصى اليسار (ما يسمى بالفلزات القلوية بما في ذلك: Li و Na و K). تحتوي هذه الذرات على إلكترون واحد في الغلاف الفرعي للثنائي، والذي يمكن التبرع به بسهولة للذرات الأخرى. في المقابل، تكون الذرات الموجودة في العمود الثاني إلى اليمين (الهالوجينات: على سبيل المثال، Cl و F و Br) بخيلة نسبيًا في مشاركة الإلكترونات. تفضل هذه الذرات كثيرًا قبول الإلكترون، لأنها مجرد إلكترون واحد خجول من غلاف مملوء («كونها نبيلة»).

    لذلك، إذا تم وضع ذرة Na بالقرب من ذرة Cl، فإن ذرة Na تتبرع بحرية بإلكترون 2 s الخاص بها وتقبله ذرة Cl بشغف. في هذه العملية، تصبح ذرة Na (في الأصل شحنة محايدة) مشحونة بشكل إيجابي وتصبح Cl (في الأصل شحنة محايدة) مشحونة سلبًا. تسمى الذرات المشحونة بالأيونات. في هذه الحالة، تكون الأيونات هي\(Na^+\)\(Cl^-\) الرمال، حيث يشير الخط العلوي إلى شحنة الأيون. يشكل الجذب الكهربائي (Coulomb) بين هذه الذرات جزيء NaCl (الملح). الرابطة الكيميائية بين أيونيين تسمى الرابطة الأيونية. هناك العديد من أنواع الروابط الكيميائية. على سبيل المثال، في جزيء الأكسجين، يتم تقاسم\(O_2\) الإلكترونات بالتساوي بين الذرات. يعتبر الترابط بين ذرات الأكسجين مثالاً على الرابطة التساهمية.