6.4: تأثير كومبتون

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• وصف تجربة كومبتون
• شرح تحول الطول الموجي لكومبتون
• وصف كيف تؤكد تجارب الأشعة السينية الطبيعة الجسيمية للإشعاع

كانت اثنتان من أفكار أينشتاين المؤثرة التي تم تقديمها في عام 1905 هي نظرية النسبية الخاصة ومفهوم الكم الخفيف، والذي نسميه الآن الفوتون. بعد عام 1905، ذهب أينشتاين إلى أبعد من ذلك ليقترح أن الموجات الكهرومغناطيسية التي تنتشر بحرية تتكون من فوتونات هي جزيئات ضوء بنفس معنى أن الإلكترونات أو الجسيمات الضخمة الأخرى هي جزيئات المادة. يمكن رؤية شعاع الضوء أحادي اللون بطول موجة$\lambda$ (أو ما يعادله من التردد$f$) إما كموجة كلاسيكية أو كمجموعة من الفوتونات التي تنتقل في فراغ بسرعة واحدة$c$ (سرعة الضوء) وكلها تحمل نفس الطاقة$E_f = hf$. أثبتت هذه الفكرة فائدتها في شرح تفاعلات الضوء مع جزيئات المادة.

قوة دفع الفوتون

على عكس جسيم المادة الذي يتميز بكتلة الراحة$m_0$، يكون الفوتون بلا كتلة. في الفراغ، على عكس جسيم المادة الذي قد يغير سرعته ولكن لا يمكنه الوصول إلى سرعة الضوء، ينتقل الفوتون بسرعة واحدة فقط، وهي بالضبط سرعة الضوء. من وجهة نظر الميكانيكا الكلاسيكية النيوتونية، تشير هاتان الخاصيتان إلى أن الفوتون لا ينبغي أن يكون موجودًا على الإطلاق. على سبيل المثال، كيف يمكننا إيجاد الزخم الخطي أو الطاقة الحركية لجسم كتلته صفر؟ تختفي هذه المفارقة الظاهرة إذا وصفنا الفوتون بأنه جسيم نسبي. وفقًا لنظرية النسبية الخاصة، فإن أي جسيم في الطبيعة يخضع لمعادلة الطاقة النسبية

$$E^2 = p^2c^2 + m_0^2c^4. \label{6.17}$$

يمكن أيضًا تطبيق هذه العلاقة على الفوتون. في المعادلة\ ref {6.17}،$E$ هي الطاقة الكلية للجسيم،$p$ وزخمه الخطي،$m_0$ وكتلة السكون. بالنسبة للفوتون، نضع$m_0 = 0$ ببساطة المعادلة\ ref {6.17}، التي تؤدي إلى التعبير$p_f$ عن زخم الفوتون

$$p_f = \dfrac{E_f}{c}. \label{6.18}$$

طاقة الفوتون هنا$E_f$ هي نفس طاقة مقدار التردد الضوئي$f$، الذي قدمناه لشرح التأثير الكهروضوئي:

$$E_f = hf = \dfrac{hc}{\lambda}. \label{6.19}$$

تنطبق علاقة الموجة التي تربط التردد$f$$λ$ بالطول الموجي والسرعة$c$ أيضًا على الفوتونات:

$$\lambda f = c \label{6.20}$$

لذلك، يمكن تمييز الفوتون بشكل متساوٍ إما بطاقته وطوله الموجي، أو تردده وزخمه. يمكن دمج المعادلات\ ref {6.19} و\ ref {6.20} في العلاقة الصريحة بين زخم الفوتون وطوله الموجي:

$$p_f = \dfrac{h}{\lambda}. \label{6.21}$$

لاحظ أن هذه المعادلة تعطينا فقط مقدار زخم الفوتون ولا تحتوي على معلومات حول الاتجاه الذي يتحرك فيه الفوتون. لتضمين الاتجاه، من المعتاد كتابة زخم الفوتون كمتجه:

$$\vec{p}_f = \hbar \vec{l}. \label{6.22}$$

في المعادلة\ ref {6.22}،$\hbar = h/2\pi$ هو ثابت بلانك المخفض (يُنطق «h-bar»)، وهو مجرد ثابت بلانك مقسومًا على العامل$2\pi$. $\vec{l}$يُطلق على المتجه اسم «ناقل الموجة» أو ناقل الانتشار (الاتجاه الذي يتحرك فيه الفوتون). يُظهر متجه الانتشار اتجاه متجه الزخم الخطي للفوتون. حجم متجه الموجة هو

$$k = |\vec{k}| = 2\pi /\lambda \nonumber$$

ويسمى رقم الموجة. لاحظ أن هذه المعادلة لا تقدم أي فيزياء جديدة. يمكننا التحقق من أن حجم المتجه في المعادلة\ ref {6.22} هو نفسه الذي قدمته المعادلة\ ref {6.18}.

تأثير كومبتون

تأثير كومبتون هو المصطلح المستخدم لنتيجة غير عادية يتم ملاحظتها عند تناثر الأشعة السينية على بعض المواد. وفقًا للنظرية الكلاسيكية، عندما تنتشر موجة كهرومغناطيسية من الذرات، من المتوقع أن يكون الطول الموجي للإشعاع المتناثر هو نفس الطول الموجي للإشعاع الساقط. على عكس هذا التنبؤ بالفيزياء الكلاسيكية، تظهر الملاحظات أنه عندما تنتشر الأشعة السينية عن بعض المواد، مثل الجرافيت، فإن الأشعة السينية المتناثرة لها أطوال موجية مختلفة عن الطول الموجي للأشعة السينية الساقطة. تمت دراسة هذه الظاهرة التي لا يمكن تفسيرها بشكل كلاسيكي بشكل تجريبي من قبل آرثر إتش كومبتون ومعاونيه، وقدم كومبتون تفسيرها في عام 1923.

لشرح التحول في الأطوال الموجية المقاسة في التجربة، استخدم كومبتون فكرة أينشتاين عن الضوء كجسيم. يحتل تأثير كومبتون مكانًا مهمًا جدًا في تاريخ الفيزياء لأنه يظهر أن الإشعاع الكهرومغناطيسي لا يمكن تفسيره على أنه ظاهرة موجية بحتة. أعطى تفسير تأثير كومبتون حجة مقنعة لمجتمع الفيزياء بأن الموجات الكهرومغناطيسية يمكن أن تتصرف بالفعل مثل تيار من الفوتونات، مما وضع مفهوم الفوتون على أرض صلبة.

الشكل$\PageIndex{1}$: إعداد تجريبي لدراسة تشتت كومبتون.

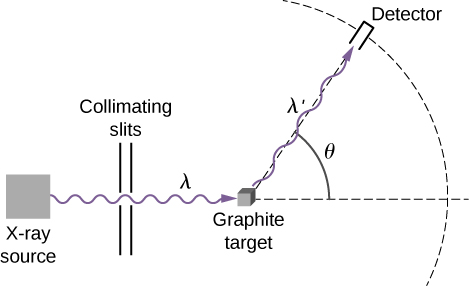
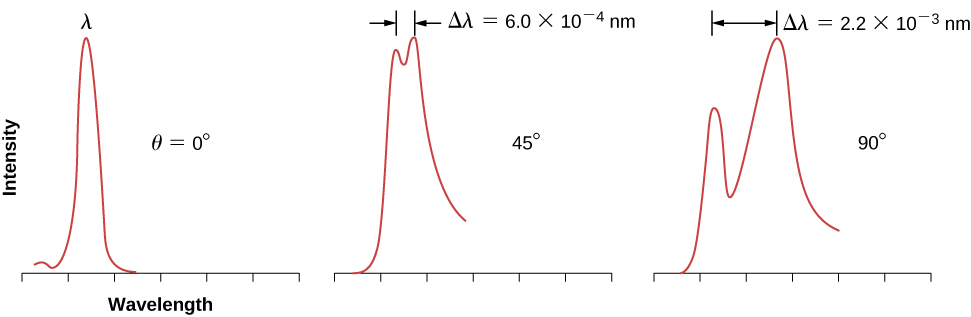
تظهر مخططات الإعداد التجريبي لـ Compton في الشكل$\PageIndex{1}$. إن فكرة التجربة واضحة: فالأشعة السينية أحادية اللون ذات الطول الموجي$λ$ تقع على عينة من الجرافيت («الهدف»)، حيث تتفاعل مع الذرات داخل العينة؛ تظهر لاحقًا في صورة أشعة سينية مبعثرة بطول موجة$λ'$. يمكن للكاشف الموجود خلف الهدف أن يقيس شدة الإشعاع المنتشر في أي اتجاه$θ$ فيما يتعلق باتجاه شعاع الأشعة السينية الساقط. زاوية التشتت هذه هي الزاوية بين اتجاه الشعاع المتناثر واتجاه الشعاع الساقط.$θ$ في هذه التجربة، نعرف شدة الشعاع الوارد ($λ$الساقط) وطوله الموجي؛ وبالنسبة لزاوية تشتت معينة$θ$، نقيس شدة وطول موجة$λ'$ الشعاع الصادر (المبعثر). تظهر النتائج النموذجية لهذه القياسات في الشكل$\PageIndex{2}$، حيث يكون$x$ المحور -هو الطول الموجي للأشعة السينية المتناثرة$y$ والمحور -هو شدة الأشعة السينية المتناثرة، المقاسة لزوايا التشتت المختلفة (المشار إليها في الرسوم البيانية). بالنسبة لجميع زوايا التشتت (باستثناء$θ=0°$)، نقيس قمتي شدة. تقع إحدى القمم عند الطول الموجي$λ$، وهو الطول الموجي للحزمة الساقطة. تقع الذروة الأخرى عند بعض الأطوال الموجية الأخرى,$λ'$. يتم فصل القمتين عن طريق ذلك$Δλ$، مما يعتمد على زاوية$θ$ تشتت الشعاع الصادر (في اتجاه المراقبة). $Δλ$يُطلق على الانفصال اسم تحول كومبتون.

الشكل$\PageIndex{2}$. يتم رسم البيانات التجريبية في هذا الشكل بوحدات عشوائية بحيث يعكس ارتفاع الملف الشخصي شدة الشعاع المتناثر فوق ضوضاء الخلفية.

كومبتون شيفت

وفقًا لما أورده كومبتون، فإن تفسير تحول كومبتون هو أنه في المادة المستهدفة، تكون إلكترونات الجرافيت والتكافؤ مرتبطة بشكل فضفاض في الذرات وتتصرف مثل الإلكترونات الحرة. افترض كومبتون أن إشعاع الأشعة السينية الساقط هو تيار من الفوتونات. يصطدم الفوتون الوارد في هذا التيار بإلكترون التكافؤ في هدف الجرافيت. في سياق هذا التصادم، ينقل الفوتون الوارد جزءًا من طاقته وزخمه إلى الإلكترون المستهدف ويترك المشهد في صورة فوتون متناثر. يشرح هذا النموذج من الناحية النوعية لماذا يكون للإشعاع المتناثر طول موجة أطول من الإشعاع الساقط. ببساطة، يظهر الفوتون الذي فقد بعضًا من طاقته كفوتون بتردد أقل، أو مكافئ، بطول موجة أطول. لإظهار أن نموذجه كان صحيحًا، استخدمه كومبتون لاشتقاق التعبير عن تحول كومبتون. افترض في استنتاجه أن كلا من الفوتون والإلكترون جسيمات نسبية وأن التصادم يخضع لمبدأين منطقيين:

1. الحفاظ على الزخم الخطي و
2. الحفاظ على الطاقة النسبية الكلية.

في الاشتقاق التالي لتحول كومبتون،$E_f$$\vec{p}_f$ ودلّل على الطاقة والزخم، على التوالي، للفوتون الساقط بالتردد$f$. يصطدم الفوتون بإلكترون نسبي في حالة سكون، مما يعني أنه قبل الاصطدام مباشرة، تكون طاقة الإلكترون بالكامل طاقة كتلة الراحة$m_0c^2$. بعد التصادم مباشرة، يتمتع الإلكترون بالطاقة$E$ والزخم$\vec{p}$، وكلاهما يفي بالمعادلة\ ref {6.19}. بعد التصادم مباشرة، يتمتع الفوتون الصادر بالطاقة$\vec{\tilde{E}}_f$$\vec{\tilde{p}}_f$ والزخم والتردد$f'$. يكون اتجاه الفوتون الساقط أفقيًا من اليسار إلى اليمين، ويكون اتجاه الفوتون الصادر في الزاوية$θ$، كما هو موضح في الشكل$\PageIndex{1}$. زاوية التشتت$θ$ هي الزاوية بين متجهات الزخم$\vec{\tilde{p}}_f$،$\vec{p}_f$ ويمكننا كتابة المنتج القياسي الخاص بها:

$$\vec{p} \cdot \vec{\tilde{p}}_f = p_f\vec{p}_f \cos \, \theta. \label{6.23}$$

بعد حجة كومبتون، نفترض أن الفوتون والإلكترون المتصادمان يشكلان نظامًا معزولًا. هذا الافتراض صالح للإلكترونات ذات الارتباط الضعيف والتي، بشكل تقريبي جيد، يمكن معالجتها كجسيمات حرة. معادلتنا الأولى هي الحفاظ على الطاقة لنظام الفوتون-الإلكترون:

$$E_f + m_0c^2 = \tilde{E}_f + E. \label{6.24}$$

الجانب الأيسر من هذه المعادلة هو طاقة النظام في اللحظة التي تسبق التصادم مباشرة، والجانب الأيمن من المعادلة هو طاقة النظام في اللحظة التي تلي التصادم مباشرة. المعادلة الثانية هي الحفاظ على الزخم الخطي لنظام الفوتون والإلكترون حيث يكون الإلكترون في حالة سكون في اللحظة التي تسبق التصادم مباشرة:

$$\vec{p}_f = \vec{\tilde{p}}_f + \vec{p}. \label{6.25}$$

الجانب الأيسر من هذه المعادلة هو زخم النظام قبل التصادم مباشرة، والجانب الأيمن من المعادلة هو زخم النظام بعد التصادم مباشرة. توجد فيزياء تشتت كومبتون بأكملها في هذه المعادلات الثلاث السابقة - الجزء المتبقي هو الجبر. في هذه المرحلة، يمكننا الانتقال إلى الصيغة الختامية لتحول كومبتون، ولكن من المفيد تسليط الضوء على الخطوات الجبرية الرئيسية التي تؤدي إلى صيغة كومبتون، والتي نقدمها هنا على النحو التالي.

نبدأ بإعادة ترتيب المصطلحات في المعادلة\ ref {6.24} وترقيمها:

$$[(E_f - \tilde{E}_f) + m_0c^2]^2 = E^2. \nonumber$$

في الخطوة التالية، نستبدل المعادلة\ ref {6.19} بكلا الجانبين ونبسطهما ونقسمهما$c^2$ للحصول عليها$E^2$

$$(E_f / c - \tilde{E}_f / c)^2 + 2m_0c (E_f / c - \tilde{E}_f / c) = p^2. \nonumber$$

الآن يمكننا استخدام Equation\ ref {6.21} للتعبير عن هذا الشكل من معادلة الطاقة بدلالة اللحظات. النتيجة هي

$$(p_f - \tilde{p}_f)^2 + 2m_0 c(p_f - \tilde{p}_f) = p^2. \label{6.26}$$

للحذف$p^2$، ننتقل إلى معادلة الزخم\ ref {6.25}، ونعيد ترتيب شروطها، ونرتبها للحصول عليها

$$\begin{align*} (\vec{p}_f - \vec{\tilde{p}}_f)^2 &= p^2 \\[4pt] &= p_f^2 + \tilde{p}_f^2 - 2p_f \tilde{p}_f \, \cos \, \theta. \end{align*} \nonumber$$

يتم إعطاء حاصل ضرب متجهات الزخم بواسطة المعادلة\ ref {6.23}. عندما نستبدل هذه النتيجة$p^2$ في المعادلة\ ref {6.26}، نحصل على معادلة الطاقة التي تحتوي على زاوية التشتت:

$$(p_f - \tilde{p}_f)^2 + 2m_0c(p_f - \tilde{p}_f) = p_f^2 + \tilde{p}_f^2 - 2p_f \tilde{p}_f \, \cos \, \theta. \nonumber$$

مع مزيد من الجبر، يمكن تبسيط هذه النتيجة إلى

$$\dfrac{1}{\tilde{p}_f} - \dfrac{1}{p_f} = \dfrac{1}{m_0c}(1 - \cos \, \theta). \label{6.27}$$

الآن تذكر المعادلة\ ref {6.21} واكتب:$1/\tilde{p}_f = \lambda' /h$ و$1/p_f = \lambda /h$. عندما يتم استبدال هذه العلاقات في المعادلة\ ref {6.27}، نحصل على علاقة تحول كومبتون:

$$\lambda' - \lambda = \dfrac{h}{m_0c}(1 - \cos \, \theta). \label{6.28}$$

$h/m_0c$ويسمى هذا العامل الطول الموجي لكومبتون للإلكترون:

$$\lambda_c = \dfrac{h}{m_0c} = 0.00243 \, nm = 2.43 \, pm. \label{6.29}$$

بالإشارة إلى التحول$\Delta \lambda = \lambda' - \lambda$، يمكن إعادة كتابة النتيجة الختامية كـ

$$\Delta \lambda = \lambda_c (1 - \cos \, \theta). \label{6.30}$$

تصف هذه الصيغة الخاصة بتحول كومبتون بشكل رائع النتائج التجريبية الموضحة في الشكل$\PageIndex{2}$. تتوافق بيانات التشتت المقاسة للموليبدينوم والجرافيت والكالسيت والعديد من المواد المستهدفة الأخرى مع هذه النتيجة النظرية. ترجع الذروة غير المتغيرة الموضحة في الشكل$\PageIndex{1}$ إلى تصادم الفوتون مع الإلكترونات الداخلية المرتبطة بإحكام في المادة المستهدفة. في الواقع، تصطدم الفوتونات التي تصطدم بالإلكترونات الداخلية للذرات المستهدفة بالذرة بأكملها. في هذه الحالة القصوى، يجب تغيير كتلة الراحة في المعادلة\ ref {6.29} إلى الكتلة الباقية للذرة. هذا النوع من التحول أصغر بأربع مرات من حيث الحجم من التحول الناتج عن التصادمات مع الإلكترونات وهو صغير جدًا بحيث يمكن إهماله.

يعد تشتت كومبتون مثالاً على التشتت غير المرن، حيث يكون للإشعاع المتناثر طول موجة أطول من الطول الموجي للإشعاع الساقط. في الاستخدام الحالي، يُستخدم مصطلح «تشتت كومبتون» للتشتت غير المرن للفوتونات بواسطة الجسيمات الحرة المشحونة. في حالة تشتت كومبتون، توفر معالجة الفوتونات كجسيمات ذات لحظات يمكن نقلها إلى جسيمات مشحونة الخلفية النظرية لشرح تحولات الطول الموجي المقاسة في التجارب؛ هذا هو الدليل على أن الإشعاع يتكون من فوتونات.

مثال$\PageIndex{1}$: Compton Scattering

تعتبر حادثة الأشعة السينية التي تبلغ مدتها 71 دقيقة حادثًا على هدف الكالسيت. أوجد الطول الموجي للأشعة السينية المتناثرة بزاوية 30°30°. ما هو أكبر تحول يمكن توقعه في هذه التجربة؟

إستراتيجية

لإيجاد الطول الموجي للأشعة السينية المتناثرة، يجب أولاً إيجاد تحول كومبتون لزاوية التشتت المعطاة$\theta = 30°$. نحن نستخدم المعادلة\ ref {6.30}. ثم نضيف هذا التحول إلى الطول الموجي الساقط للحصول على الطول الموجي المتناثر. يحدث أكبر تحول في كومبتون$\theta$ عند الزاوية عندما تكون$1 - \cos \, \theta$ له القيمة الأكبر، وهي الزاوية$\theta = 180°$.

الحل

التحول في$\theta = 30°$ هو

$$\begin{align*} \Delta \lambda &= \lambda_c (1 - \cos \, 30°) \\[4pt] &= 0.134 \lambda_c \\[4pt] &= (0.134)(2.43) \, pm \\[4pt] &= 0.32 \end{align*} \nonumber$$

هذا يعطي الطول الموجي المتناثر:

$$\begin{align*} \lambda' &= \lambda + \Delta \lambda \\[4pt] &= (71 + 0.325) \, pm \\[4pt] &= 71.325 \,pm. \end{align*} \nonumber$$

التحول الأكبر هو

$$\begin{align*} (\Delta \lambda )_{max} &= \lambda_c(1 − \cos \, 180°) \\[4pt] &= 2(2.43 \, pm) \\[4pt] &= 4.86 \, pm. \end{align*} \nonumber$$

الدلالة

تم اكتشاف أكبر تحول في الطول الموجي للإشعاع المرتد؛ ومع ذلك، فإن معظم الفوتونات من الشعاع الساقط تمر عبر الهدف ويتم تشتيت جزء صغير فقط من الفوتونات (عادةً، أقل من 5٪). لذلك، تتطلب هذه القياسات أجهزة كشف شديدة الحساسية.

التمارين$\PageIndex{1}$

تعتبر حادثة الأشعة السينية التي تبلغ مدتها 71 دقيقة حادثًا على هدف الكالسيت. أوجد الطول الموجي للأشعة السينية المتناثرة بزاوية ٦٠ درجة. ما أصغر نوبة يمكن توقعها في هذه التجربة؟

إجابة

$(\Delta \lambda)_{min} = 0 \, m$بزاوية 0 درجة؛$71.0 \, pm + 0.5 \lambda_c = 72.215 \, pm$