6.3: التأثير الكهروضوئي
- Page ID
- 196618
في نهاية هذا القسم، ستتمكن من:
- وصف الخصائص الفيزيائية للتأثير الكهروضوئي
- اشرح لماذا لا يمكن تفسير التأثير الكهروضوئي بالفيزياء الكلاسيكية
- وصف كيف تفسر فكرة أينشتاين عن جسيم الإشعاع التأثير الكهروضوئي
عندما يتعرض سطح معدني لموجة كهرومغناطيسية أحادية اللون ذات طول موجي قصير بما فيه الكفاية (أو ما يعادل ذلك، فوق تردد الحد الأدنى)، يتم امتصاص الإشعاع الساقط وينبعث السطح المكشوف إلكترونات. تُعرف هذه الظاهرة بالتأثير الكهروضوئي. تسمى الإلكترونات المنبعثة في هذه العملية بالإلكترونات الضوئية.
يظهر الإعداد التجريبي لدراسة التأثير الكهروضوئي بشكل تخطيطي في الشكل\(\PageIndex{1}\). تعمل المادة المستهدفة كالأنود، الذي يصبح باعثًا للإلكترونات الضوئية عندما يتم إضاءته بإشعاع أحادي اللون. نحن نسمي هذا القطب الكهربائي. يتم جمع الإلكترونات الضوئية عند الكاثود، والذي يتم الاحتفاظ به عند جهد أقل فيما يتعلق بالأنود. يمكن زيادة الفرق المحتمل بين الأقطاب الكهربائية أو تقليله، أو يمكن عكس قطبيته. يتم وضع الأقطاب الكهربائية في أنبوب زجاجي تم إخلاؤه حتى لا تفقد الإلكترونات الضوئية طاقتها الحركية عند الاصطدام بجزيئات الهواء في الفراغ بين الأقطاب الكهربائية.
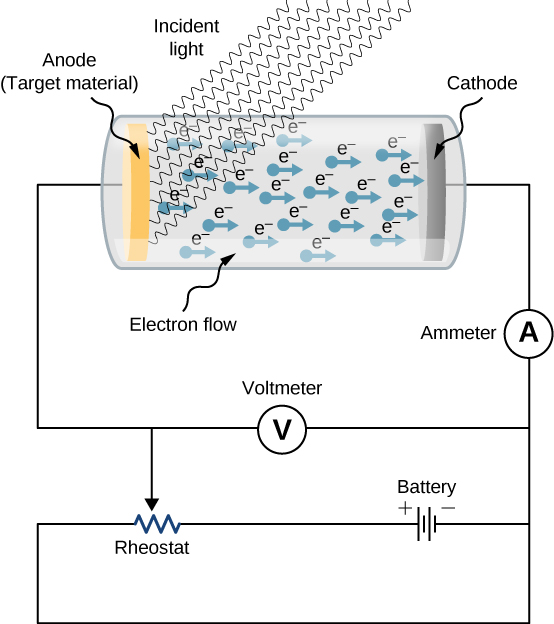
عندما لا تتعرض المادة المستهدفة للإشعاع، لا يتم تسجيل أي تيار في هذه الدائرة لأن الدائرة مكسورة (لاحظ وجود فجوة بين الأقطاب الكهربائية). ولكن عندما تكون المادة المستهدفة متصلة بالطرف السالب للبطارية وتتعرض للإشعاع، يتم تسجيل تيار في هذه الدائرة؛ ويسمى هذا التيار بالتيار الضوئي. لنفترض أننا الآن نعكس فرق الجهد بين الأقطاب الكهربائية بحيث تتصل المادة المستهدفة الآن بالطرف الموجب للبطارية، ثم نزيد الجهد ببطء. يتلاشى التيار الضوئي تدريجيًا ويتوقف في النهاية عن التدفق تمامًا عند بعض قيمة هذا الجهد المعكوس. يُطلق على الفرق المحتمل الذي يتوقف عنده التيار الضوئي عن التدفق إمكانات التوقف.
خصائص التأثير الكهروضوئي
يتميز التأثير الكهروضوئي بثلاث خصائص مهمة لا يمكن تفسيرها بالفيزياء الكلاسيكية: (1) عدم وجود فترة تأخير، (2) استقلالية الطاقة الحركية للإلكترونات الضوئية عن شدة الإشعاع الساقط، و (3) وجود تردد القطع. دعونا نفحص كل من هذه الخصائص.
غياب وقت التأخير
عندما يضرب الإشعاع المادة المستهدفة في القطب، تنبعث الإلكترونات على الفور تقريبًا، حتى عند شدة منخفضة جدًا للإشعاع الساقط. يتناقض غياب التأخير هذا مع فهمنا القائم على الفيزياء الكلاسيكية. تتنبأ الفيزياء الكلاسيكية بأنه بالنسبة للإشعاع منخفض الطاقة، سيستغرق الأمر وقتًا طويلاً قبل أن تتمكن الإلكترونات المشععة من اكتساب طاقة كافية لمغادرة سطح القطب؛ ومع ذلك، لا يتم ملاحظة مثل هذا التراكم للطاقة.
شدة الإشعاع الساقط والطاقة الحركية للإلكترونات الضوئية
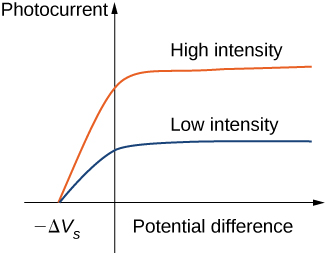
تظهر المنحنيات التجريبية النموذجية في الشكل\(\PageIndex{2}\)، حيث يتم رسم التيار الضوئي مقابل فرق الجهد المطبق بين الأقطاب الكهربائية. بالنسبة للاختلاف الإيجابي المحتمل، ينمو التيار بشكل مطرد حتى يصل إلى مرحلة الاستقرار. إن زيادة الزيادة المحتملة بعد هذه النقطة لا تؤدي إلى زيادة التيار الضوئي على الإطلاق. تنتج الكثافة العالية للإشعاع قيمة أعلى للتيار الضوئي. بالنسبة للاختلاف السلبي المحتمل، مع زيادة القيمة المطلقة لفرق الجهد، تنخفض قيمة التيار الضوئي وتصبح صفرًا عند إمكانية التوقف. بالنسبة لأي شدة للإشعاع الساقط، سواء كانت الكثافة عالية أو منخفضة، تظل قيمة إمكانية التوقف دائمًا عند قيمة واحدة.
لفهم سبب كون هذه النتيجة غير عادية من وجهة نظر الفيزياء الكلاسيكية، علينا أولاً تحليل طاقة الإلكترونات الضوئية. الإلكترون الضوئي الذي يخرج من السطح لديه طاقة حركية\(K\). لقد اكتسبت هذه الطاقة من الموجة الكهرومغناطيسية الساقطة. في الفراغ بين الأقطاب الكهربائية، يتحرك الإلكترون الضوئي في الجهد الكهربائي وتتغير طاقته بالكمية\(q \Delta V\)، وأين\(\Delta V\) فرق الجهد و\(q = -e\). نظرًا لعدم وجود قوى سوى القوة الكهربائية، من خلال تطبيق نظرية العمل والطاقة، نحصل على توازن\(\Delta K - e\Delta V = 0\) الطاقة للإلكترون الضوئي،\(\Delta K\) أين التغيير في الطاقة الحركية للإلكترون الضوئي. عندما\(-\Delta V_s\) يتم تطبيق إمكانات التوقف، يفقد الإلكترون الضوئي طاقته الحركية الأولية\(K_i\) ويستريح. وهكذا، يصبح توازن الطاقة الخاص بها\((0 - K_i) - e(-\Delta V_s) = 0\)، هكذا\(K_i = e\Delta V_s\). في ظل وجود إمكانات التوقف، فإن أكبر طاقة حركية يمكن\(K_{max}\) أن يمتلكها الإلكترون الضوئي هي طاقته الحركية الأولية، التي توجد على سطح الإلكترود الضوئي. لذلك، يمكن قياس أكبر طاقة حركية للإلكترونات الضوئية مباشرة عن طريق قياس إمكانات التوقف:
\[K_{max} = e\Delta V_s. \label{PEexpt} \]
في هذه المرحلة يمكننا أن نرى أين تتعارض النظرية الكلاسيكية مع النتائج التجريبية. في النظرية الكلاسيكية، تمتص الإلكترون الضوئي الطاقة الكهرومغناطيسية بطريقة مستمرة؛ وهذا يعني أنه عندما يكون الإشعاع الساقط ذا كثافة عالية، فمن المتوقع أن تكون الطاقة الحركية في المعادلة\ ref {PeExpt} عالية. وبالمثل، عندما تكون كثافة الإشعاع منخفضة، من المتوقع أن تكون الطاقة الحركية منخفضة. لكن التجربة تظهر أن الطاقة الحركية القصوى للإلكترونات الضوئية مستقلة عن شدة الضوء.
وجود تردد القطع
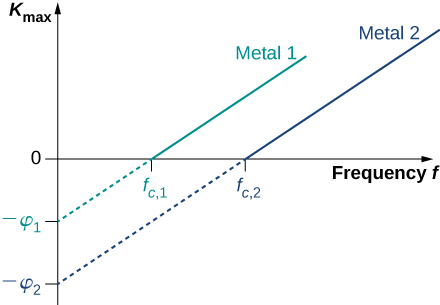
بالنسبة لأي سطح معدني، يوجد حد أدنى لتردد الإشعاع الساقط الذي لا يحدث تحته تيار ضوئي. قيمة تردد القطع هذا للتأثير الكهروضوئي هي خاصية فيزيائية للمعدن: المواد المختلفة لها قيم مختلفة لتردد القطع. تظهر البيانات التجريبية اتجاهًا خطيًا نموذجيًا (الشكل\(\PageIndex{3}\)). تنمو الطاقة الحركية للإلكترونات الضوئية على السطح خطيًا مع زيادة وتيرة الإشعاع الساقط. تعطي القياسات لجميع الأسطح المعدنية مخططات خطية بمنحدر واحد. لا تتوافق أي من هذه الظواهر المرصودة مع الفهم الكلاسيكي للطبيعة. وفقًا للوصف الكلاسيكي، يجب ألا تعتمد الطاقة الحركية للإلكترونات الضوئية على تردد الإشعاع الساقط على الإطلاق، ويجب ألا يكون هناك تردد مقطوع. بدلاً من ذلك، في الصورة الكلاسيكية، تستقبل الإلكترونات الطاقة من الموجة الكهرومغناطيسية الساقطة بطريقة مستمرة، وتعتمد كمية الطاقة التي تتلقاها فقط على شدة الضوء الساقط ولا شيء آخر. لذلك في الفهم الكلاسيكي، طالما كان الضوء ساطعًا، فمن المتوقع أن يستمر التأثير الكهروضوئي.
وظيفة العمل
تم شرح التأثير الكهروضوئي في عام 1905 من قبل أ. أينشتاين. استنتج أينشتاين أنه إذا كانت فرضية بلانك حول كميات الطاقة صحيحة لوصف تبادل الطاقة بين الإشعاع الكهرومغناطيسي وجدران التجويف، فيجب أن تعمل أيضًا على وصف امتصاص الطاقة من الإشعاع الكهرومغناطيسي عن طريق سطح القطب الضوئي. افترض أن الموجة الكهرومغناطيسية تحمل طاقتها في حزم منفصلة. تتجاوز فرضية أينشتاين فرضية بلانك لأنها تنص على أن الضوء نفسه يتكون من كميات الطاقة. بمعنى آخر، تنص على أن الموجات الكهرومغناطيسية يتم قياسها كميًا.
في نهج أينشتاين، يتكون شعاع من الضوء أحادي اللون\(f\) من التردد من فوتونات. الفوتون هو جسيم من الضوء. يتحرك كل فوتون بسرعة الضوء ويحمل كمية الطاقة\(E_f\). تعتمد طاقة الفوتون فقط على تردده\(f\). بشكل صريح، طاقة الفوتون هي
\[E_f = hf \label{planck} \]
\(h\)أين ثابت بلانك. في التأثير الكهروضوئي، تصل الفوتونات إلى السطح المعدني ويعطي كل فوتون كل طاقته لإلكترون واحد فقط على سطح المعدن. هذا النقل للطاقة من الفوتون إلى الإلكترون هو من نوع «الكل أو لا شيء»، ولا توجد عمليات نقل كسرية يفقد فيها الفوتون جزءًا فقط من طاقته ويبقى على قيد الحياة. إن جوهر الظاهرة الكمومية هو إما أن ينقل الفوتون طاقته بالكامل ويتوقف عن الوجود أو لا يوجد نقل على الإطلاق. هذا على النقيض من الصورة الكلاسيكية، حيث يُسمح بنقل الطاقة الجزئية. بناءً على هذا الفهم الكمي، فإن توازن الطاقة للإلكترون على السطح الذي يتلقى الطاقة\(E_f\) من الفوتون هو
\[E_f = K_{max} + \phi \nonumber \]
\(K_max\)أين الطاقة الحركية، المعطاة بواسطة المعادلة\ ref {PeExpt}، التي يمتلكها الإلكترون في اللحظة التي ينفصل فيها عن السطح. في معادلة توازن الطاقة هذه،\(\phi\) هي الطاقة اللازمة لفصل الإلكترون الضوئي عن السطح. هذه الطاقة\(\phi\) تسمى وظيفة عمل المعدن. كل معدن له وظيفة العمل المميزة، كما هو موضح في الجدول\(\PageIndex{1}\). للحصول على الطاقة الحركية للإلكترونات الضوئية على السطح، نقوم ببساطة بعكس معادلة توازن الطاقة واستخدام المعادلة\ ref {planck} للتعبير عن طاقة الفوتون الممتص. يعطينا هذا التعبير عن الطاقة الحركية للإلكترونات الضوئية، والتي تعتمد بشكل صريح على تردد الإشعاع الساقط:
\[K_{max}=hf−ϕ \label{PEeffect} \]
المعادلة\ ref {PeEffect} لها شكل رياضي بسيط ولكن فيزياءها عميقة. يمكننا الآن توضيح المعنى المادي وراء هذه المعادلة.
| المعدن | \(\phi\)(EV) |
|---|---|
| نا | \ (\ phi\) (eV) ">2.46 |
| جميع | \ (\ phi\) (eV) ">4.08 |
| الرصاص | \ (\ phi\) (eV) ">4.14 |
| ZN | \ (\ phi\) (eV) ">4.31 |
| عنصر الحديد | \ (\ phi\) (eV) ">4.50 |
| كوب | \ (\ phi\) (eV) ">4.70 |
| العمر | \ (\ phi\) (eV) ">4.73 |
| وعاء | \ (\ phi\) (eV) ">6.35 |
في تفسير أينشتاين، تحدث التفاعلات بين الإلكترونات الفردية والفوتونات الفردية. يعني عدم وجود فترة تأخير أن هذه التفاعلات الفردية تحدث على الفور. لا يمكن زيادة وقت التفاعل هذا عن طريق خفض شدة الضوء. تتوافق شدة الضوء مع عدد الفوتونات التي تصل إلى السطح المعدني لكل وحدة زمنية. حتى في شدة الإضاءة المنخفضة جدًا، لا يزال التأثير الكهروضوئي يحدث لأن التفاعل يكون بين إلكترون واحد وفوتون واحد. طالما أن هناك فوتون واحد على الأقل لديه طاقة كافية لنقله إلى إلكترون مقيد، سيظهر إلكترون ضوئي على سطح الإلكترود الضوئي.
يأتي وجود تردد\(f_c\) القطع للتأثير الكهروضوئي من المعادلة\ ref {PeEffect} لأن الطاقة\(K_{max}\) الحركية للإلكترون الضوئي يمكن أن تأخذ قيمًا موجبة فقط. هذا يعني أنه يجب أن يكون هناك تردد حدسي تكون فيه الطاقة الحركية صفرًا\(0 = hf_c - \phi\). بهذه الطريقة، نحصل على الصيغة الصريحة لتردد القطع:
\[f_c = \frac{\phi}{h}. \label{6.15} \]
يعتمد تردد القطع فقط على وظيفة عمل المعدن وهو يتناسب بشكل مباشر معه. عندما تكون وظيفة العمل كبيرة (عندما ترتبط الإلكترونات بسرعة بالسطح المعدني)، يجب أن تكون طاقة الفوتون العتبي كبيرة لإنتاج إلكترون ضوئي، ومن ثم يكون تردد العتبة المقابل كبيرًا. تنتج الفوتونات ذات الترددات الأكبر من تردد العتبة\(f_c\) دائمًا إلكترونات ضوئية لأنها موجودة\(K_{max} > 0\). \(f_c\)لا تمتلك الفوتونات ذات الترددات الأصغر من الطاقة الكافية لإنتاج إلكترونات ضوئية. لذلك، عندما يكون للإشعاع الساقط تردد أقل من تردد القطع، لا يتم ملاحظة التأثير الكهروضوئي. نظرًا لأن التردد\(f\) والطول الموجي\(\lambda\) للموجات الكهرومغناطيسية مرتبطان بالعلاقة الأساسية\(\lambda f = c\) (حيث تكون cc هي سرعة الضوء في الفراغ)، فإن تردد القطع له الطول الموجي المقطوع المقابل\(\lambda_c\):
\[\lambda_c = \frac{c}{f_c} = \frac{c}{\phi /h} = \frac{hc}{\phi}. \label{6.16} \]
في هذه المعادلة،\(hc = 1240 \, eV \cdot nm\). يمكن إعادة صياغة ملاحظاتنا بالطريقة المكافئة التالية: عندما يكون للإشعاع الساقط أطوال موجية أطول من الطول الموجي المقطوع، لا يحدث التأثير الكهروضوئي.
يقع الإشعاع بطول موجة 300 نانومتر على سطح فضي. هل ستتم ملاحظة الإلكترونات الضوئية؟
إستراتيجية
لا يمكن إخراج الإلكترونات الضوئية من سطح المعدن إلا عندما يكون للإشعاع الساقط طول موجة أقصر من الطول الموجي المقطوع. وظيفة عمل الفضة هي\(\phi = 4.73 \, eV\) (الجدول\(\PageIndex{1}\)). لإجراء التقدير، نستخدم المعادلة\ ref {6.16}.
الحل
الحد الأقصى لطول الموجة لمراقبة التأثير الكهروضوئي في الفضة هو
\[\begin{align*} \lambda_c &= \frac{hc}{\phi} \\[4pt] &= \frac{1240 \, eV \cdot nm}{4.73 \, eV} = 262 \, nm. \end{align*} \nonumber \]
يبلغ طول موجة الإشعاع الساقط 300 نانومتر، وهو أطول من الطول الموجي المقطوع؛ لذلك لا يتم ملاحظة الإلكترونات الضوئية.
الدلالة
إذا كان القطب الضوئي مصنوعًا من الصوديوم بدلاً من الفضة، فسيكون الطول الموجي المقطوع 504 نانومتر وستتم ملاحظة الإلكترونات الضوئية.
تخبرنا المعادلة\ ref {PeEffect} في نموذج أينشتاين أن الطاقة الحركية القصوى للإلكترونات الضوئية هي دالة خطية لتردد الإشعاع الساقط، وهو موضح في الشكل\(\PageIndex{3}\). بالنسبة لأي معدن، فإن منحدر هذه القطعة له قيمة ثابت بلانك. يمنحنا التقاطع مع\(K_{max}\) المحور -قيمة دالة العمل المميزة للمعدن. من ناحية أخرى،\(K_{max}\) يمكن قياسها مباشرة في التجربة عن طريق قياس قيمة إمكانات التوقف\(\delta V_s\) (انظر المعادلة\ ref {PeExpt}) التي يتوقف عندها التيار الضوئي. تسمح لنا هذه القياسات المباشرة بتحديد قيمة ثابت بلانك بشكل تجريبي، وكذلك وظائف عمل المواد.
يقدم نموذج أينشتاين أيضًا شرحًا مباشرًا لقيم التيار الضوئي الموضحة في الشكل\(\PageIndex{3}\). على سبيل المثال، تؤدي مضاعفة شدة الإشعاع إلى مضاعفة عدد الفوتونات التي تضرب السطح لكل وحدة زمنية. كلما زاد عدد الفوتونات، زاد عدد الإلكترونات الضوئية، مما يؤدي إلى تيار ضوئي أكبر في الدائرة. هذه هي الطريقة التي تؤثر بها شدة الإشعاع على التيار الضوئي. يجب أن يصل التيار الضوئي إلى مرحلة الاستقرار عند بعض قيم الاختلاف المحتمل لأن عدد الإلكترونات الضوئية، في وقت الوحدة، يساوي عدد الفوتونات الساقطة ولا يعتمد عدد الفوتونات الساقطة على فرق الجهد المطبق على الإطلاق، ولكن فقط على شدة الإشعاع الساقط. لا تتغير إمكانية التوقف مع شدة الإشعاع لأن الطاقة الحركية للإلكترونات الضوئية (انظر المعادلة\ ref {PeEffect}) لا تعتمد على شدة الإشعاع.
عند استخدام ضوء 180 نانومتر في تجربة مع معدن غير معروف، ينخفض التيار الضوئي المقاس إلى الصفر عند الجهد - 0.80 فولت. حدد وظيفة عمل المعدن وتردد قطعه للتأثير الكهروضوئي.
إستراتيجية
للعثور على تردد القطع\(f_c\)، نستخدم Equation\ ref {6.15}، ولكن يجب علينا أولاً العثور على وظيفة العمل\(\phi\). للبحث\(\phi\)، نستخدم المعادلة\ ref {Peexpt} والمعادلة\ ref {peEffect}. ينخفض التيار الضوئي إلى الصفر عند قيمة إيقاف الإمكانات، لذلك نحدد\(\Delta V_s = 0.8 V\).
الحل
نستخدم المعادلة\ ref {PeExpt} للعثور على الطاقة الحركية للإلكترونات الضوئية:
\[K_{max} = e\Delta V_s = e(0.80 V) = 0.80 \, eV. \nonumber \]
الآن نحل المعادلة من أجل\(\phi\):
\[\phi = hf - K_{max} = \frac{hc}{\lambda} - K_{max} = \frac{1240 \, eV \cdot m}{180 \, nm} − 0.80 \, eV = 6.09eV. \nonumber \]
أخيرًا، نستخدم المعادلة للعثور على تردد القطع:
\[f_c = \frac{\phi}{h} \frac{6.09 \, eV}{4.136 \times 10^{-15} eV \cdot s} = 1.47 \times 10^{-15} Hz. \nonumber \]
الدلالة
في العمليات الحسابية مثل تلك الموضحة في هذا المثال، من الملائم استخدام ثابت بلانك في الوحدات\(eV \cdot s\) والتعبير عن جميع الطاقات في eV بدلاً من الجول.
يسقط ضوء بنفسجي طوله 430 نانومتر على قطب كهربائي ضوئي للكالسيوم بوظيفة عمل تبلغ 2.71 eV. أوجد طاقة الفوتونات الساقطة وأقصى طاقة حركية للإلكترونات المقذوفة.
إستراتيجية
طاقة الفوتون الساقط هي\(E_f = hf = hc/\lambda\)، المكان الذي نستخدمه\(f\lambda = c\). للحصول على الطاقة القصوى للإلكترونات المقذوفة، نستخدم المعادلة\ ref {6.16}.
الحل
\[E_f = \frac{hc}{\lambda} = \frac{1240 \, eV \cdot nm}{430 \, nm} = 2.88 \, eV, \, K_{max} = E_f − \phi = 2.88 \, eV − 2.71 \, eV = 0.17 \, eV \nonumber \]
الدلالة
في هذا الإعداد التجريبي، تتوقف الإلكترونات الضوئية عن التدفق عند إمكانية التوقف البالغة 0.17 فولت.
يسقط ضوء أصفر يبلغ 589 نانومتر على سطح تكون وظيفة عمله 1.20 eV. ما هي إمكانات التوقف؟ ما الطول الموجي المقطوع؟
- إجابة
-
\(-0.91 \, V\)1040 نانومتر
تردد القطع للتأثير الكهروضوئي في بعض المواد هو\(8.0×10^{13}Hz.\) عندما يكون للضوء الساقط تردد\(1.2×10^{14}Hz\)، يتم قياس إمكانية التوقف على النحو - 0.16 فولت. تقدير قيمة ثابت بلانك من هذه البيانات (بوحدات Jsj·s و Evsev · s) وتحديد النسبة المئوية للخطأ الخاص بك تقدير.
- إجابة
-
\(h = 6.40 \times 10^{-34} J \cdot s = 4.0 \times 10^{-15} eV \cdot s\)؛\(-3.5\%\)


