6.2: إشعاع الجسم الأسود
- Page ID
- 196569
في نهاية هذا القسم، ستتمكن من:
- قم بتطبيق قوانين Wien و Stefan لتحليل الإشعاع المنبعث من الجسم الأسود
- شرح فرضية بلانك عن كميات الطاقة
تصدر جميع الأجسام إشعاعات كهرومغناطيسية عبر مجموعة من الأطوال الموجية. في فصل سابق، تعلمنا أن الجسم الأكثر برودة يشع بطاقة أقل من الجسم الأكثر دفئًا. نعلم أيضًا من خلال الملاحظة أنه عندما يتم تسخين الجسم وترتفع درجة حرارته، يتغير الطول الموجي المتصور للإشعاع المنبعث من الأشعة تحت الحمراء إلى اللون الأحمر، ثم من الأحمر إلى البرتقالي، وهكذا دواليك. مع ارتفاع درجة حرارته، يضيء الجسم بالألوان المقابلة للأطوال الموجية الأصغر من الطيف الكهرومغناطيسي. هذا هو المبدأ الأساسي للمصباح المتوهج: يضيء الفتيل المعدني الساخن باللون الأحمر، وعندما يستمر التسخين، يغطي توهجه في النهاية الجزء المرئي بالكامل من الطيف الكهرومغناطيسي. تحدد درجة الحرارة (T) للجسم الذي يصدر الإشعاع، أو الباعث، الطول الموجي الذي تكون عنده الطاقة المشعة عند الحد الأقصى. على سبيل المثال، تشع الشمس، التي تتراوح درجة حرارة سطحها بين 5000 كلفن و 6000 كلفن، بقوة أكبر في نطاق من الأطوال الموجية حوالي 560 نانومتر في الجزء المرئي من الطيف الكهرومغناطيسي. يشع جسمك، عندما تكون درجة حرارته العادية حوالي 300 كلفن، بقوة أكبر في جزء الأشعة تحت الحمراء من الطيف.
يتم امتصاص الإشعاع الذي يقع على جسم ما جزئيًا وينعكس جزئيًا. في حالة التوازن الديناميكي الحراري، يكون المعدل الذي يمتص به الجسم الإشعاع هو نفس المعدل الذي ينبعث به. لذلك، فإن الامتصاص الجيد للإشعاع (أي جسم يمتص الإشعاع) يعد أيضًا باعثًا جيدًا. يمتص الممتص المثالي كل الإشعاع الكهرومغناطيسي الساقط عليه؛ ويسمى هذا الجسم بالجسم الأسود.

على الرغم من أن الجسم الأسود مثالي، لأنه لا يوجد جسم مادي يمتص 100٪ من الإشعاع الساقط، يمكننا بناء إدراك وثيق لجسم أسود في شكل ثقب صغير في جدار حاوية مغلقة تعرف باسم مشعاع التجويف، كما هو موضح في الشكل\(\PageIndex{1}\). تكون الجدران الداخلية لمبرد التجويف خشنة ومسودة بحيث يصبح أي إشعاع يدخل من خلال ثقب صغير في جدار التجويف محاصرًا داخل التجويف. عند التوازن الديناميكي الحراري (عند درجة حرارة T)، تمتص جدران التجويف نفس القدر من الإشعاع الذي تنبعث منه. علاوة على ذلك، داخل التجويف، يتم موازنة الإشعاع الداخل إلى الحفرة بالإشعاع الخارج منها. يمكن الحصول على طيف انبعاث الجسم الأسود من خلال تحليل الضوء المشع من الحفرة. تسمى الموجات الكهرومغناطيسية المنبعثة من الجسم الأسود بإشعاع الجسم الأسود.
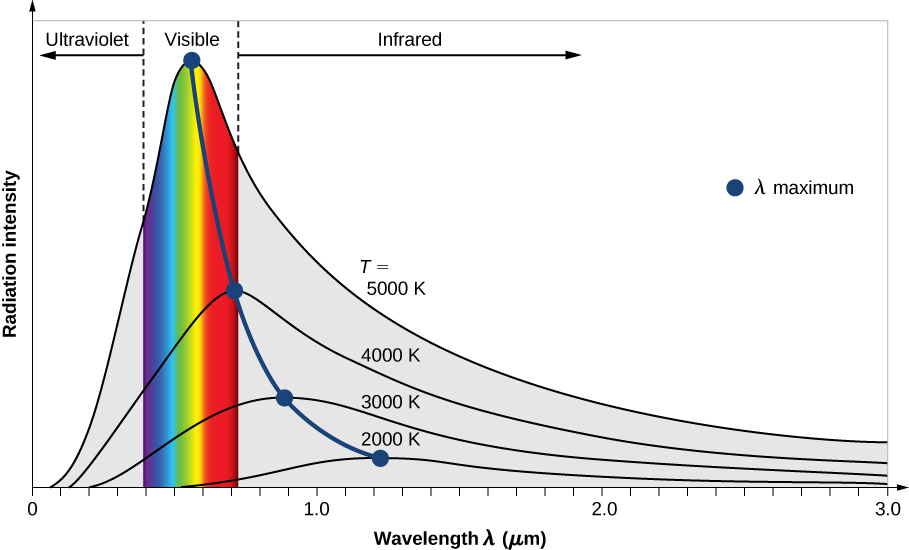
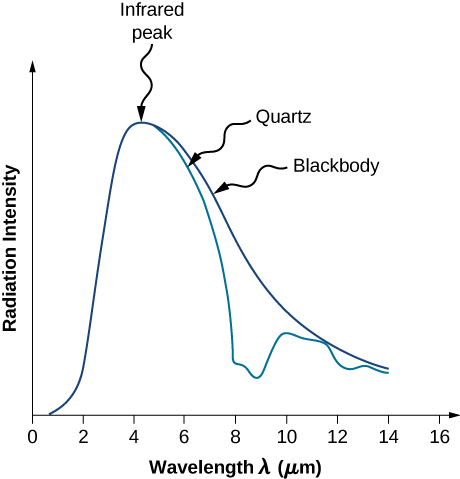
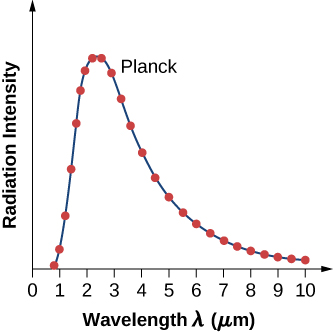
تعتمد\(I(\lambda, T)\) شدة إشعاع الجسم الأسود على الطول الموجي\(\lambda\) للإشعاع المنبعث وعلى درجة حرارة T للجسم الأسود (الشكل\(\PageIndex{2}\)). الوظيفة\(I(\lambda, T)\) هي كثافة الطاقة التي يتم إشعاعها لكل وحدة طول موجة؛ بمعنى آخر، إنها الطاقة المشعة لكل وحدة مساحة من الثقب في رادياتير التجويف لكل وحدة طول موجة. وفقًا لهذا التعريف،\(I(\lambda, T)d\lambda\) هي الطاقة لكل وحدة مساحة تنبعث في فترة الطول الموجي من\(\lambda\) إلى\(\lambda + d\lambda\). تمت دراسة توزيع الكثافة بين الأطوال الموجية للإشعاع المنبعث من التجاويف بشكل تجريبي في نهاية القرن التاسع عشر. بشكل عام، يتبع الإشعاع المنبعث من المواد تقريبًا منحنى إشعاع الجسم الأسود (الشكل\(\PageIndex{3}\))؛ ومع ذلك، فإن أطياف النجوم الشائعة تتبع منحنى إشعاع الجسم الأسود عن كثب.
يلخص قانونان مهمان النتائج التجريبية لإشعاع الجسم الأسود: قانون النزوح في فيينا وقانون ستيفان. قانون الإزاحة الخاص بـ Wien موضح في الشكل\(\PageIndex{2}\) من خلال المنحنى الذي يربط الحد الأقصى على منحنيات الكثافة. في هذه المنحنيات، نرى أنه كلما زادت حرارة الجسم، كلما كان الطول الموجي المقابل لذروة الانبعاث في منحنى الإشعاع أقصر. من الناحية الكمية، ينص قانون فيينا
\[\lambda_{max}T = 2.898 \times 10^{-3} m \cdot K \label{Wien} \]
أين\(\lambda_{max}\) هو موضع الحد الأقصى في منحنى الإشعاع. بعبارة أخرى،\(\lambda_{max}\) هو الطول الموجي الذي يشع عنده الجسم الأسود بقوة أكبر عند درجة حرارة معينة T. لاحظ أنه في المعادلة\ ref {Wien}، تكون درجة الحرارة بالكلفن. يسمح لنا قانون الإزاحة الخاص بـ Wien بتقدير درجات حرارة النجوم البعيدة عن طريق قياس الطول الموجي للإشعاع الذي تنبعث منه.
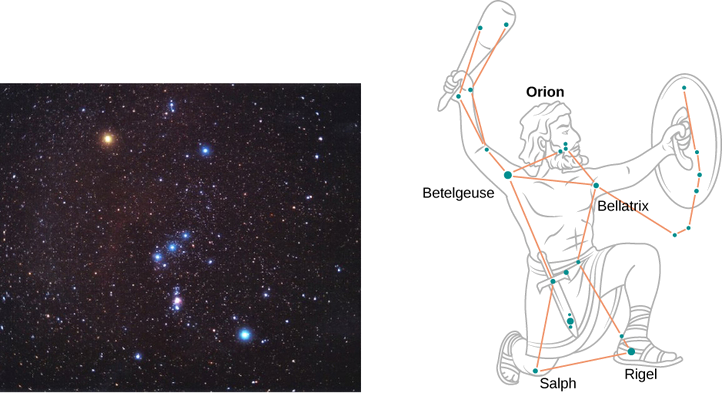
في أمسية صافية خلال أشهر الشتاء، إذا كنت في نصف الكرة الشمالي ونظرت إلى السماء، يمكنك رؤية كوكبة Orion (The Hunter). يومض أحد النجوم في هذه الكوكبة، وهو Rigel، باللون الأزرق والنجم الآخر، Betelgeuse، لونه ضارب إلى الحمرة، كما هو موضح في الشكل\(\PageIndex{4}\). أي من هذين النجمين هو كولر، منجل أو ريجل؟
إستراتيجية
نتعامل مع كل نجم على أنه جسم أسود. ثم وفقًا لقانون فيينا، تتناسب درجة حرارته عكسيًا مع الطول الموجي لشدة الذروة. الطول الموجي\(\lambda_{max}^{(blue)}\) للضوء الأزرق أقصر\(\lambda_{max}^{(red)}\) من الطول الموجي للضوء الأحمر. حتى لو لم نعرف الأطوال الموجية الدقيقة، فلا يزال بإمكاننا إعداد نسبة.
الحل
نكتب قانون فيينا للنجمة الزرقاء والنجمة الحمراء، لدينا
\[\begin {align*} \lambda_{max}^{(red)}T_{(red)} &= 2.898 \times 10^{-3} m \cdot K \\[5pt] &= \lambda_{max}^{(blue)} T_{(blue)} \end{align*} \nonumber \]
عند التبسيط، يعطي هذا
\[T_{(red)} = \dfrac{\lambda_{max}^{(blue)}}{\lambda_{max}^{(red)}}T_{(blue)} < T_{(blue)} \nonumber \]
لذلك، فإن منجل الجوزاء أكثر برودة من Rigel.
الدلالة
لاحظ أن قانون الإزاحة في فيينا يخبرنا أنه كلما ارتفعت درجة حرارة الجسم الباعث، كلما كان الطول الموجي للإشعاع الذي ينبعث منه أقصر. التحليل النوعي المقدم في هذا المثال صالح بشكل عام لأي جسم مصدر، سواء كان جسمًا كبيرًا مثل النجم أو جسمًا صغيرًا مثل الفتيل المتوهج في المصباح المتوهج.
لشعلة الشمعة المعطرة بالخوخ لونها أصفر ولهب موقد بنسن في مختبر الكيمياء لونه مزرق. أي شعلة ذات درجة حرارة أعلى؟
- إجابة
العلاقة التجريبية الثانية هي قانون ستيفان، الذي يتعلق بالطاقة الكلية لإشعاع الجسم الأسود المنبعث عبر الطيف الكامل للأطوال الموجية عند درجة حرارة معينة. في\(\PageIndex{2}\)، يتم تمثيل هذه الطاقة الكلية بالمنطقة الموجودة أسفل منحنى إشعاع الجسم الأسود لـ T معين. مع زيادة درجة حرارة الجسم الأسود، يزداد إجمالي الطاقة المنبعثة أيضًا. من الناحية الكمية، يعبر قانون ستيفان عن هذه العلاقة على النحو التالي:
\[P(T) = \sigma AT^4 \nonumber \]
\(A\)أين مساحة سطح الجسم الأسود،\(T\) ودرجة حرارته (بالكلفن)،\(σ\) وثابت ستيفان-بولتزمان،\(\sigma = 5.670 \times 10^{-8} W/(m^2 \cdot K^4)\). يتيح لنا قانون ستيفان تقدير مقدار الطاقة التي يشعها النجم عن طريق قياس درجة حرارته عن بُعد.
سيتطور نجم مثل شمسنا في النهاية إلى نجم «عملاق أحمر» ثم إلى نجم «قزم أبيض». يبلغ حجم القزم الأبيض النموذجي حجم الأرض تقريبًا، ودرجة حرارة سطحه حوالي\(2.5 \times 10^4 K\). العملاق الأحمر النموذجي له درجة حرارة سطح\(3.0 \times 10^3 K\) ونصف قطر أكبر بحوالي 100,000 مرة من قزم أبيض. ما متوسط القدرة المشعة لكل وحدة مساحة وإجمالي الطاقة المشعة لكل نوع من هذه الأنواع من النجوم؟ كيف يقارنون؟
إستراتيجية
إذا تعاملنا مع النجم كجسم أسود، فوفقًا لقانون ستيفان، فإن القوة الكلية التي يشعها النجم تتناسب مع القوة الرابعة لدرجة حرارته. للعثور على الطاقة المشعة لكل وحدة مساحة من السطح، لا نحتاج إلى وضع أي افتراضات حول شكل النجم لأن P/ A يعتمد فقط على درجة الحرارة. ومع ذلك، لحساب الطاقة الكلية، نحتاج إلى افتراض أن الطاقة تشع من خلال سطح كروي يحيط بالنجم، بحيث تكون مساحة السطح\(A = 4\pi R^2\)، حيث R هي نصف قطره.
الحل
تعطي نسبة بسيطة تستند إلى قانون ستيفان
\[\dfrac{P_{dwarf}/A_{dwarf}}{P_{giant}/A_{giant}} = \dfrac{\sigma T_{dwarf}^4}{\sigma T_{giant}^4} = \left(\dfrac{T_{dwarf}}{T_{giant}}\right)^4 = 4820 \label{6.5} \]
تبلغ الطاقة المنبعثة لكل وحدة مساحة بواسطة قزم أبيض حوالي 5000 مرة من الطاقة المنبعثة من العملاق الأحمر. عند الإشارة إلى هذه النسبة\(a=4.8×10^3\)، تعطي المعادلة\ ref {6.5}
\[\dfrac{P_{dwarf}}{P_{giant}} = \alpha \dfrac{A_{dwarf}}{A_{giant}} = \alpha \dfrac{4\pi R_{dwarf}^2}{4\pi R_{giant}^2} = \alpha \left( \dfrac{R_{dwarf}}{R_{giant}} \right)^2 = 4.8 \times 10^{−7} \nonumber \]
نرى أن الطاقة الكلية المنبعثة من القزم الأبيض هي جزء صغير من إجمالي الطاقة المنبعثة من العملاق الأحمر. على الرغم من انخفاض درجة الحرارة نسبيًا، فإن الطاقة الإجمالية التي يشعها العملاق الأحمر تتجاوز بكثير قوة القزم الأبيض لأن العملاق الأحمر له مساحة سطح أكبر بكثير. لتقدير القيمة المطلقة للطاقة المنبعثة لكل وحدة مساحة، نستخدم قانون ستيفان مرة أخرى. بالنسبة للقزم الأبيض، نحصل على
\[\dfrac{P_{dwarf}}{A_{dwarf}} = \sigma T_{dwarf}^4 = 5.670 \times 10^{-8} \dfrac{W}{m^2 \cdot K^4} (2.5 \times 10^4 \, K)^4 = 2.2 \times 10^{10} \dfrac{W}{m^2} \label{6.7} \]
يتم الحصول على النتيجة المماثلة للعملاق الأحمر عن طريق قياس النتيجة للقزم الأبيض:
\[\dfrac{P_{giant}}{A_{giant}} = \dfrac{2.2 \times 10^{10}}{4.82 \times 10^3} \dfrac{W}{m^2} = 4.56 \times 10^6 \dfrac{W}{m^2} \cong 4.6 \times 10^{-6} \dfrac{W}{m^2} \nonumber \]
الدلالة
لتقدير الطاقة الإجمالية المنبعثة من القزم الأبيض، من حيث المبدأ، يمكننا استخدام المعادلة\ ref {6.7}. ومع ذلك، للعثور على مساحة سطحه، نحتاج إلى معرفة متوسط نصف القطر، والذي لم يرد في هذا المثال. لذلك، يتوقف الحل هنا. وينطبق الشيء نفسه أيضًا على النجم الأحمر العملاق.
يتم تسخين لعبة البوكر الحديدية. مع ارتفاع درجة الحرارة، تبدأ لعبة البوكر في التوهج - أولاً باللون الأحمر الباهت، ثم الأحمر الفاتح، ثم البرتقالي، ثم الأصفر. استخدم إما منحنى إشعاع الجسم الأسود أو قانون فيينا لشرح هذه التغييرات في لون التوهج.
- إجابة
-
يتناقص الطول الموجي للحد الأقصى للإشعاع مع زيادة درجة الحرارة.
لنفترض أن\(α\) نجمين\(β\) يشعان بالضبط نفس القوة الكلية. إذا كان نصف قطر النجم\(α\) يساوي ثلاثة أضعاف نصف قطر النجم\(β\)، فما النسبة بين درجات حرارة سطح هذه النجوم؟ أيهما أكثر سخونة؟
- إجابة
-
\(T_{\alpha}/T_{\beta} = 1/\sqrt{3} \cong 0.58\)، لذا\(\beta\) فإن النجم أكثر سخونة.
صاغ غوستاف آر كيرشوف مصطلح «الجسم الأسود» في عام 1862. كان منحنى إشعاع الجسم الأسود معروفًا بشكل تجريبي، لكن شكله استعصى على التفسير المادي حتى عام 1900. النموذج المادي للجسم الأسود عند درجة حرارة T هو نموذج الموجات الكهرومغناطيسية المغلقة في التجويف (الشكل\(\PageIndex{1}\)) وعند التوازن الديناميكي الحراري مع جدران التجويف. يمكن للموجات تبادل الطاقة مع الجدران. الهدف هنا هو إيجاد توزيع كثافة الطاقة بين أنماط الاهتزاز المختلفة بأطوال موجية (أو ترددات) مختلفة. بمعنى آخر، نريد أن نعرف مقدار الطاقة التي يحملها طول موجة واحد أو نطاق من الأطوال الموجية. بمجرد معرفة توزيع الطاقة، يمكننا استخدام الأساليب الإحصائية القياسية (على غرار تلك التي تمت دراستها في الفصل السابق) للحصول على منحنى إشعاع الجسم الأسود وقانون ستيفان وقانون الإزاحة في فيينا. عندما يكون النموذج المادي صحيحًا، يجب أن تكون التنبؤات النظرية هي نفس المنحنيات التجريبية.
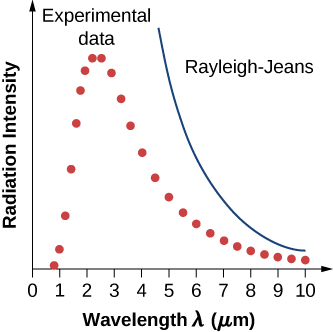
في النهج الكلاسيكي لمشكلة إشعاع الجسم الأسود، حيث يتم التعامل مع الإشعاع كموجات (كما درست في الفصول السابقة)، تكون أنماط الموجات الكهرومغناطيسية المحتبسة في التجويف في حالة توازن وتتبادل طاقاتها باستمرار مع جدران التجويف. لا يوجد سبب مادي يجعل الموجة تفعل خلاف ذلك: يمكن استبدال أي كمية من الطاقة، إما عن طريق نقلها من الموجة إلى المادة الموجودة في الجدار أو باستقبالها للموجة من المادة الموجودة في الجدار. هذه الصورة الكلاسيكية هي أساس النموذج الذي طوره اللورد رايلي وبشكل مستقل من قبل السير جيمس جينز. تُعرف نتيجة هذا النموذج الكلاسيكي لمنحنيات إشعاع الجسم الأسود باسم قانون Rayleigh-Jeans. ومع ذلك، كما هو موضح في الشكل\(\PageIndex{5}\)، يفشل قانون Rayleigh-Jeans في إعادة إنتاج النتائج التجريبية بشكل صحيح. في حدود الأطوال الموجية القصيرة، يتنبأ قانون Rayleigh-Jeans بكثافة الإشعاع اللانهائية، وهو ما يتعارض مع النتائج التجريبية التي تحتوي فيها كثافة الإشعاع على قيم محدودة في المنطقة فوق البنفسجية من الطيف. يُظهر هذا الاختلاف بين نتائج النظرية الكلاسيكية والتجارب، والتي أصبحت تسمى كارثة الأشعة فوق البنفسجية، كيف تفشل الفيزياء الكلاسيكية في تفسير آلية إشعاع الجسم الأسود.
تم حل مشكلة إشعاع الجسم الأسود في عام 1900 بواسطة ماكس بلانك. استخدم بلانك نفس فكرة نموذج Rayleigh-Jeans بمعنى أنه عالج الموجات الكهرومغناطيسية بين الجدران داخل التجويف بشكل كلاسيكي، وافترض أن الإشعاع في حالة توازن مع جدران التجويف. الفكرة المبتكرة التي قدمها بلانك في نموذجه هي افتراض أن إشعاع التجويف ينشأ من التذبذبات الذرية داخل جدران التجويف، وأن هذه التذبذبات يمكن أن تحتوي فقط على قيم منفصلة للطاقة. لذلك، يمكن للإشعاع المحبوس داخل جدران التجويف تبادل الطاقة مع الجدران بكميات منفصلة فقط. تفترض فرضية بلانك لقيم الطاقة المنفصلة، والتي أطلق عليها اسم الكوانتا، أن المذبذبات داخل جدران التجويف تحتوي على طاقات كمية. كانت هذه فكرة جديدة تمامًا تجاوزت الفيزياء الكلاسيكية للقرن التاسع عشر لأنه، كما تعلمت في فصل سابق، في الصورة الكلاسيكية، يمكن لطاقة المذبذب أن تأخذ أي قيمة مستمرة. افترض بلانك أن طاقة المذبذب (\(E_n\)) يمكن أن تحتوي فقط على قيم منفصلة أو كمية:
\[E_n = nhf, \, where \, n = 1,2,3, \ldots \label{eq30} \]
في المعادلة\ ref {eq30}،\(f\) هو تردد مذبذب بلانك. يُطلق على الرقم الطبيعي\(n\) الذي يعدد هذه الطاقات المنفصلة الرقم الكمي. \(h\)يسمى الثابت المادي ثابت بلانك:
\[h = 6.626 \times 10^{-34} J \cdot s = 4.136 \times 10^{-15} eV \cdot s \label{6.10} \]
تتوافق كل قيمة طاقة منفصلة مع الحالة الكمومية لمذبذب بلانك. يتم تعداد الحالات الكمومية بالأرقام الكمومية. على سبيل المثال، عندما يكون مذبذب بلانك في حالته\(n 1\) الكمومية الأولى، تكون طاقته\(E_1 = hf\)؛ وعندما يكون في الحالة\(n = 2\) الكمومية، تكون طاقته\(E_2 = 2hf\)؛ عندما يكون في الحالة\(n = 3\) الكمومية\(E_3 = 3hf\)؛ وهكذا.
لاحظ أن المعادلة\ ref {eq30} تُظهر أن هناك عددًا لا نهائيًا من الحالات الكمومية، والتي يمكن تمثيلها كتسلسل {hf، 2 hf، 3 hf،...، (n - 1) hf، nhf، (n + 1) hf،...}. يتم فصل كل حالتين كموميتين متتاليتين في هذا التسلسل بقفزة طاقة,\(\delta E = hf\). يمكن للمذبذب الموجود في الجدار أن يستقبل الطاقة من الإشعاع الموجود في التجويف (الامتصاص)، أو يمكن أن يعطي الطاقة للإشعاع الموجود في التجويف (الانبعاث). ترسل عملية الامتصاص المذبذب إلى حالة كمية أعلى، وترسل عملية الانبعاث المذبذب إلى حالة كمية أقل. أيًا كانت الطريقة التي يسير بها تبادل الطاقة هذا، فإن أصغر كمية من الطاقة يمكن تبادلها هي hf. لا يوجد حد أعلى لمقدار الطاقة التي يمكن تبادلها، ولكن كل ما يتم تبادله يجب أن يكون عددًا صحيحًا مضاعفًا لـ hf. إذا كانت حزمة الطاقة لا تحتوي على هذه الكمية بالضبط، فلن يتم امتصاصها أو انبعاثها من جدار الجسم الأسود.
تنص فرضية بلانك عن كميات الطاقة على أن كمية الطاقة المنبعثة من المذبذب تحملها كمية الإشعاع،\(\Delta E\):
\[\Delta E = hf \label{planck} \]
تذكر أن تردد الإشعاع الكهرومغناطيسي مرتبط بطول الموجة وسرعة الضوء من خلال\(f\lambda = c\). This means that we can express معادلة العلاقة الأساسية\ ref {6.10} بالتساوي من حيث الطول الموجي\(\lambda\). When included in the computation of the energy density of a blackbody, Planck’s hypothesis gives the following theoretical expression for the power intensity of emitted radiation per unit wavelength:
\[I(\lambda, T) = \dfrac{2\pi hc^2}{\lambda^5} \dfrac{1}{e^{hc/\lambda k_BT} - 1} \label{6.11} \]
حيث c هي سرعة الضوء في الفراغ و kBkB هو ثابت بولتزمان،\(k_B = 1.380 \times 10^{-23} J/K\). تسمى الصيغة النظرية المعبر عنها في المعادلة\ ref {6.11} قانون إشعاع الجسم الأسود الخاص بـ Planck. يتوافق هذا القانون مع منحنى إشعاع الجسم الأسود التجريبي (الشكل\(\PageIndex{2}\)). بالإضافة إلى ذلك، يمكن اشتقاق كل من قانون النزوح في فيينا وقانون ستيفان من المعادلة\ ref {6.11}. لاشتقاق قانون الإزاحة الخاص بـ Wien، نستخدم حساب التفاضل لإيجاد الحد الأقصى لمنحنى شدة الإشعاع\(I(\lambda, T)\). لاشتقاق قانون ستيفان وإيجاد قيمة ثابت Stefan-Boltzmann، نستخدم حساب التفاضل والتكامل\(I(\lambda, T)\) لإيجاد الطاقة الكلية التي يشعها جسم أسود عند درجة حرارة واحدة في كامل طيف الأطوال الموجية من\(\lambda = 0\) إلى\(\lambda = \infty\). تم ترك هذا الاشتقاق كتمرين لاحقًا في هذا الفصل.
يهتز مذبذب كمي في جدار التجويف في الشكل\(\PageIndex{1}\) بتردد\(5.0 \times 10^{14} Hz\). احسب المسافات بين مستويات الطاقة.
إستراتيجية
يتم إعطاء حالات الطاقة للمذبذب الكمي بواسطة المعادلة\ ref {eq30}. \(\Delta E\)يتم الحصول على تباعد الطاقة من خلال إيجاد فرق الطاقة بين حالتين كموميتين متجاورتين للأعداد الكمومية n + 1 و n.
الحل
يمكننا استبدال التردد المعطى وثابت بلانك مباشرة في المعادلة:
\[\begin {align*} \Delta E &= E_{n + 1} − En = (n + 1)hf − nhf \\[5pt] &= hf \\[5pt] &= (6.626 \times 10^{−34} \, J \cdot s)(5.0 \times 10^{14} \, Hz) \\[5pt] &= 3.3 \times 10^{− 19} \, J \end{align*} \nonumber \]
الدلالة
لاحظ أننا لا نحدد نوع المواد المستخدمة لبناء التجويف. هنا، المذبذب الكمي هو نموذج نظري لذرة أو جزيء مادة في الجدار.
يهتز الجزيء بتردد يبلغ\(5.0 \times 10^{14}\, Hz\). ما أصغر مسافة بين مستويات الطاقة الاهتزازية؟
- إجابة
-
\(3.3 \times 10^{-19} J\)
تتأرجح كتلة مقدارها ١٫٠ كجم في نهاية زنبرك ثابت زنبركي مقداره ١٠٠٠ نيوتن/متر، وسعة هذه التذبذبات تساوي ٠٫١٠ م، استخدم مفهوم القياس الكمي لإيجاد تباعد الطاقة لهذا المذبذب الكلاسيكي. هل تحديد كمية الطاقة مهم للأنظمة العيانية، مثل هذا المذبذب؟
إستراتيجية
نستخدم المعادلة\ ref {planck} كما لو كان النظام مذبذبًا كموميًا، ولكن بتردد f للكتلة يهتز على زنبرك. لتقييم ما إذا كان للتحديد الكمي تأثير كبير أم لا، فإننا نقارن تباعد الطاقة الكمومية بالطاقة الكلية العيانية لهذا المذبذب الكلاسيكي.
الحل
بالنسبة لثابت الزنبرك\(k = 1.0 \times 10^3 N/m\)، فإن تردد الكتلة، 2\(m = 1.0 \, kg\)، هو
\[f = \dfrac{1}{2\pi} \sqrt{\dfrac{k}{m}} = \dfrac{1}{2\pi} \sqrt{\dfrac{1.0 \times 10^3 N/m}{1.0 \, kg}} \simeq 5.0 \, Hz \nonumber \]
كمية الطاقة التي تتوافق مع هذا التردد هي
\[\Delta E = hf = (6.626 \times 10^{-34} J \cdot s)(5.0 \, Hz) = 3.3 \times 10^{-33} J \nonumber \]
عندما تكون الاهتزازات ذات سعة\(A = 0.10 \, m\)، تكون طاقة التذبذبات
\[E = \dfrac{1}{2} kA^2 = \dfrac{1}{2}(1000 \, N/m)(0.1 \, m)^2 = 5.0 \, J \nonumber \]
الدلالة
وهكذا، بالنسبة للمذبذب الكلاسيكي، لدينا\(\Delta E/E \approx 10^{-34}\). نرى أن فصل مستويات الطاقة صغير للغاية. لذلك، لجميع الأغراض العملية، تأخذ طاقة المذبذب الكلاسيكي قيمًا مستمرة. هذا هو السبب في إمكانية تطبيق المبادئ الكلاسيكية على الأنظمة العيانية التي تتم مواجهتها في الحياة اليومية دون فقدان الدقة.
هل ستكون النتيجة في المثال\(\PageIndex{4}\) مختلفة إذا لم تكن الكتلة ١٫٠ كجم بل كتلة صغيرة مقدارها ١٫٠ g، وكانت سعة الاهتزازات ٠٫١٠ m؟
- إجابة
-
لا، لأنه حينها\(\Delta E /E \approx 10^{-21}\)
عندما نشر بلانك نتائجه لأول مرة، لم تؤخذ فرضية كميات الطاقة على محمل الجد من قبل مجتمع الفيزياء لأنها لم تنبع من أي نظرية فيزيائية راسخة في ذلك الوقت. كان يُنظر إليها، حتى من قبل بلانك نفسه، على أنها خدعة رياضية مفيدة أدت إلى «ملاءمة» نظرية جيدة للمنحنى التجريبي. تم تغيير هذا التصور في عام 1905 عندما نشر أينشتاين شرحه للتأثير الكهروضوئي، حيث أعطى كمية طاقة بلانك معنى جديدًا: جسيم الضوء.


