6.5: نموذج بور لذرة الهيدروجين
- Page ID
- 196597
في نهاية هذا القسم، ستكون قادرًا على:
- اشرح الفرق بين طيف الامتصاص وطيف انبعاث الإشعاع المنبعث من الذرات
- وصف تجربة رذرفورد للرقائق الذهبية واكتشاف النواة الذرية
- شرح التركيب الذري للهيدروجين
- وصف افتراضات نظرية الكم المبكرة لذرة الهيدروجين
- لخص كيف يشرح نموذج Bohr الكمومي لذرة الهيدروجين الطيف الإشعاعي للهيدروجين الذري
تاريخيًا، كان نموذج Bohr لذرة الهيدروجين هو النموذج الأول للهيكل الذري الذي شرح بشكل صحيح أطياف الإشعاع للهيدروجين الذري. يحتل النموذج مكانة خاصة في تاريخ الفيزياء لأنه أدخل نظرية الكم المبكرة، والتي أحدثت تطورات جديدة في الفكر العلمي وبلغت ذروتها لاحقًا في تطوير ميكانيكا الكم. لفهم تفاصيل نموذج بوهر، يجب علينا أولاً مراجعة اكتشافات القرن التاسع عشر التي دفعت إلى صياغته.
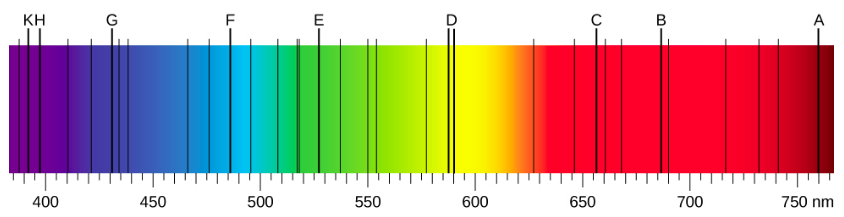
عندما نستخدم المنشور لتحليل الضوء الأبيض القادم من الشمس، يتم ملاحظة عدة خطوط داكنة في الطيف الشمسي (الشكل\(\PageIndex{1}\)). تُسمى خطوط امتصاص الطاقة الشمسية بخطوط فراونهوفر نسبة إلى جوزيف فون فراونهوفر، الذي قام بقياس أطوال موجاتها بدقة. خلال الفترة 1854-1861، اكتشف غوستاف كيرشوف وروبرت بنسن أنه بالنسبة للعناصر الكيميائية المختلفة، فإن طيف الانبعاث الخطي لعنصر ما يطابق تمامًا طيف الامتصاص الخطي الخاص به. يوضح الشكل الفرق بين طيف الامتصاص وطيف الانبعاثات\(\PageIndex{2}\).
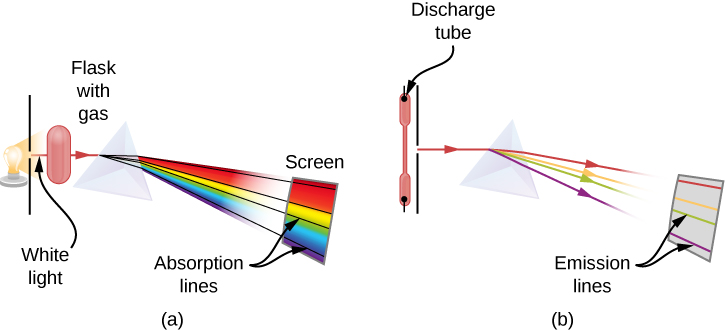
يتم ملاحظة طيف الامتصاص عندما يمر الضوء عبر الغاز. يظهر هذا الطيف كخطوط سوداء تحدث فقط عند أطوال موجية معينة على خلفية الطيف المستمر للضوء الأبيض (الشكل\(\PageIndex{2}\)). تخبرنا الأطوال الموجية المفقودة بالأطوال الموجية للإشعاع التي يمتصها الغاز. يتم ملاحظة طيف الانبعاث عندما ينبعث الضوء من الغاز. يُنظر إلى هذا الطيف كخطوط ملونة على الخلفية السوداء (الأشكال\(\PageIndex{3}\) و\(\PageIndex{4}\)). تخبرنا مواقع خطوط الانبعاثات بالأطوال الموجية للإشعاع المنبعثة من الغاز. كل عنصر كيميائي له طيف انبعاث مميز خاص به. بالنسبة لكل عنصر، تكون مواضع خطوط الانبعاثات الخاصة به مطابقة تمامًا لمواضع خطوط الامتصاص الخاصة به. وهذا يعني أن ذرات عنصر معين تمتص الإشعاع فقط بأطوال موجية محددة وأن الإشعاع الذي لا يحتوي على هذه الأطوال الموجية لا يمتصه العنصر على الإطلاق. وهذا يعني أيضًا أن الإشعاع المنبعث من ذرات كل عنصر له نفس الأطوال الموجية تمامًا مثل الإشعاع الذي تمتصه.


أطياف انبعاث العناصر لها هياكل معقدة؛ تصبح أكثر تعقيدًا بالنسبة للعناصر ذات الأعداد الذرية الأعلى. ينتمي الطيف الأبسط، الموضح في الشكل\(\PageIndex{4}\)، إلى ذرة الهيدروجين. يمكن رؤية أربعة خطوط فقط للعين البشرية. وكما تقرأ من اليمين إلى اليسار في الشكل\(\PageIndex{4}\)، فإن هذه الخطوط هي: الأحمر (656 نانومتر)، الذي يسمى\(H-\alpha\) الخط؛ والأزرق (486 نانومتر) والأزرق (434 نانومتر) والبنفسجي (410 نانومتر). تظهر الخطوط ذات الأطوال الموجية الأقصر من 400 نانومتر في الجزء فوق البنفسجي من الطيف (الشكل\(\PageIndex{4}\)، أقصى اليسار) وهي غير مرئية للعين البشرية. هناك عدد لا نهائي من الخطوط الطيفية غير المرئية في سلسلة الهيدروجين.
اكتشف يوهان بالمر في عام 1885 صيغة تجريبية لوصف مواقع (الأطوال الموجية)》لخطوط انبعاث الهيدروجين في هذه السلسلة. تُعرف باسم صيغة Balmer:
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - \dfrac{1}{n^2}\right). \label{balmer} \]
\(R_H = 1.09737 \times 10^7 m^{-1}\)يسمى الثابت ثابت Rydberg للهيدروجين. في المعادلة\ ref {balmer}، يأخذ العدد الصحيح الموجب n قيمًا\(n = 3, 4,5,6\) للخطوط الأربعة المرئية في هذه السلسلة. تسمى سلسلة خطوط الانبعاثات التي تقدمها صيغة Balmer سلسلة Balmer للهيدروجين. تم وصف خطوط انبعاث الهيدروجين الأخرى التي تم اكتشافها في القرن العشرين بواسطة صيغة Rydberg، التي تلخص جميع البيانات التجريبية:
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{n_f^2} - \dfrac{1}{n_i^2}\right)\label{rydberg} \]
أين\(n_i = n_f > n_i\) (في خطوات عددية).
عندما\(n_f = 1\) تسمى سلسلة الخطوط الطيفية سلسلة ليمان. عندما\(n_f = 2\) تسمى السلسلة سلسلة Balmer، وفي هذه الحالة، تتزامن صيغة Rydberg مع صيغة Balmer (Equation\ ref {balmer}). عندما\(n_f = 3\) تسمى السلسلة سلسلة Paschen. عندما\(n_f = 4\) تسمى السلسلة سلسلة Brackett. عندما\(n_f = 5\) تسمى السلسلة سلسلة Pfund. عندما تكون\(n_f = 6\) لدينا سلسلة همفريز. كما قد يتبادر إلى ذهنك، هناك عدد لا نهائي من هذه النطاقات الطيفية في طيف الهيدروجين لأنه\(n_f\) يمكن أن يكون أي رقم صحيح موجب.
تعطي صيغة Rydberg للهيدروجين المواضع الدقيقة للخطوط الطيفية كما يتم ملاحظتها في المختبر؛ ومع ذلك، في بداية القرن العشرين، لم يستطع أحد تفسير سبب نجاحها بشكل جيد. ظلت صيغة Rydberg غير مفسرة حتى تم اقتراح أول نموذج ناجح لذرة الهيدروجين في عام 1913.
احسب الأطوال الموجية الأطول والأقصر في سلسلة Balmer.
إستراتيجية
يمكننا استخدام صيغة بالمر (المعادلة\ ref {balmer}) أو صيغة Rydberg (المعادلة\ ref {rydberg}). يتم الحصول على أطول طول موجي\(1/n_i\) عندما يكون أكبر، وهو متى\(n_i = n_f + 1 = 3\)، بسبب\(n_f = 2\) سلسلة Balmer. يتم الحصول على أصغر طول موجي عندما\(1/n_i\) يكون الأصغر، وهو\(1/n_i \rightarrow 0\) متى\(n_i \rightarrow \infty\).
الحل
حد الموجة الطويلة:
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - \dfrac{1}{3^2}\right) = (1.09737 \times 10^7) \dfrac{1}{m} \left( \dfrac{1}{4} - \dfrac{1}{9}\right) \Rightarrow \lambda = 656.3 \, nm \nonumber \]
حد الموجة القصيرة:
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - 0\right) = (1.09737 \times 10^7) \dfrac{1}{m} \left( \dfrac{1}{4} \right) \Rightarrow \lambda = 364.6 \, nm. \nonumber \]
الدلالة
لاحظ أن هناك عددًا لا نهائيًا من الخطوط الطيفية الواقعة بين هذين الحدين.
ما هي حدود سلسلة Lyman؟ هل يمكنك رؤية هذه الخطوط الطيفية؟
- إجابة
-
121.5 نانومتر و 91.1 نانومتر؛ لا، هذه النطاقات الطيفية موجودة في الأشعة فوق البنفسجية
مفتاح حل لغز الأطياف الذرية هو فهم البنية الذرية. لقد عرف العلماء منذ فترة طويلة أن المادة مصنوعة من الذرات. وفقًا لعلم القرن التاسع عشر، تعد الذرات أصغر كميات غير قابلة للتجزئة من المادة. تم تحطيم هذا الاعتقاد العلمي من خلال سلسلة من التجارب الرائدة التي أثبتت وجود جسيمات دون ذرية، مثل الإلكترونات والبروتونات والنيوترونات.
تم اكتشاف الإلكترون وتحديده كأصغر كمية من الشحنة الكهربائية بواسطة J.J. Thomson في عام 1897 في تجاربه على أشعة الكاثود، والمعروفة أيضًا باسم تجارب أشعة بيتا: A β -ray عبارة عن شعاع من الإلكترونات. في عام 1904، اقترح طومسون النموذج الأول للهيكل الذري، المعروف باسم نموذج «حلوى البرقوق»، حيث تتكون الذرة من مادة غير معروفة ذات شحنة موجبة مع إلكترونات سالبة مضمنة فيها مثل البرقوق في الحلوى. حوالي عام 1900، صنف إي روثرفورد، وبشكل مستقل، بول أولريش فيلارد، جميع الإشعاعات المعروفة في ذلك الوقت باسم\(\alpha\)\(β\) - الأشعة،\(\gamma\) - الأشعة، و - الأشعة (الأشعة\(\gamma\) السينية هي شعاع من الفوتونات عالية الطاقة). في عام 1907، استخدم روثرفورد وتوماس رويدز طرق التحليل الطيفي لإظهار أن جزيئات\(\alpha\) الإشعاع الموجبة الشحنة (تسمى\(\alpha\) الجسيمات -) هي في الواقع ذرات الهيليوم المؤينة بشكل مضاعف. في عام 1909، استخدم روثرفورد وإرنست مارسدن وهانز جيجر\(\alpha\) الجسيمات الإلكترونية في تجربة التشتت الشهيرة التي دحضت نموذج طومسون (انظر الزخم الخطي والتصادمات).
في تجربة رذرفورد للرقائق الذهبية (المعروفة أيضًا باسم تجربة Geiger-Marsden)، وقعت جزيئات ألفا على رقائق ذهبية رقيقة وتناثرت بذرات الذهب داخل الرقاقة (انظر أنواع التصادمات). تم اكتشاف الجسيمات الصادرة من خلال شاشة تلألؤ بزاوية 360 درجة تحيط بالهدف الذهبي (للحصول على وصف تفصيلي للإعداد التجريبي، انظر الزخم الخطي والتصادمات). عندما اصطدم جسيم متناثر بالشاشة، لوحظ وميض صغير من الضوء (التلألؤ) في ذلك الموقع. من خلال حساب التلألقات التي شوهدت في زوايا مختلفة فيما يتعلق باتجاه الشعاع الساقط، تمكن العلماء من تحديد جزء الجسيمات الساقطة المتناثرة والكسر الذي لم ينحرف على الإطلاق. إذا كان نموذج بودنغ البرقوق صحيحًا، فلن تكون هناك جزيئات ألفا متناثرة في الخلف. ومع ذلك، أظهرت نتائج تجربة روثرفورد أنه على الرغم من ظهور جزء كبير من جزيئات ألفا من الرقاقة غير المنتشرة على الإطلاق كما لو أن الرقاقة لم تكن في طريقها، إلا أن جزءًا كبيرًا من جزيئات ألفا عادت إلى الانتشار باتجاه المصدر. كان هذا النوع من النتائج ممكنًا فقط عندما تتركز معظم الكتلة والشحنة الموجبة الكاملة لذرة الذهب في مساحة صغيرة داخل الذرة.
في عام 1911، اقترح روثرفورد نموذجًا نوويًا للذرة. في نموذج روثرفورد، احتوت الذرة على نواة ذات شحنة موجبة ذات حجم ضئيل، تقريبًا مثل النقطة، ولكنها تضمنت كتلة الذرة بأكملها تقريبًا. تحتوي الذرة أيضًا على إلكترونات سالبة كانت موجودة داخل الذرة ولكنها بعيدة نسبيًا عن النواة. بعد عشر سنوات، صاغ روثرفورد اسم البروتون لنواة الهيدروجين واسم النيوترون لجسيم افتراضي محايد كهربائيًا من شأنه أن يتوسط في ربط البروتونات الموجبة في النواة (تم اكتشاف النيوترون في عام 1932 من قبل جيمس تشادويك). يعود الفضل إلى رذرفورد في اكتشاف النواة الذرية؛ ومع ذلك، فإن نموذج روثرفورد للبنية الذرية لا يفسر صيغة Rydberg لخطوط انبعاث الهيدروجين.
كان نموذج بوهر لذرة الهيدروجين، الذي اقترحه نيلز بور في عام 1913، أول نموذج كمي يشرح بشكل صحيح طيف انبعاث الهيدروجين. يجمع نموذج Bohr بين الميكانيكا الكلاسيكية لحركة الكواكب والمفهوم الكمي للفوتونات. بمجرد أن أثبت روثرفورد وجود النواة الذرية، أصبح حدس بوهر بأن الإلكترون السالب في ذرة الهيدروجين يجب أن يدور حول النواة الموجبة نتيجة منطقية لقانون المسافة العكسية للجاذبية الكهروستاتيكية. تذكر أن قانون كولوم الذي يصف الجاذبية بين شحنتين متقابلتين له شكل مشابه لقانون نيوتن العالمي للجاذبية بمعنى أن قوة الجاذبية والقوة الكهروستاتيكية تتناقص حيث\(1/r^2\) r هي المسافة الفاصلة بين الأجسام . وبنفس الطريقة التي تدور بها الأرض حول الشمس، يمكن للإلكترون السالب في ذرة الهيدروجين أن يدور حول النواة الإيجابية. ومع ذلك، فإن الشحنة المتسارعة تشع طاقتها. من الناحية الكلاسيكية، إذا تحرك الإلكترون حول النواة بطريقة كوكبية، فسيخضع لتسارع الجاذبية المركزية، وبالتالي سيكون بمثابة طاقة مشعة من شأنها أن تتسبب في انزلاقه إلى النواة. لن تكون ذرة الهيدروجين الكوكبية هذه مستقرة، وهو ما يتعارض مع ما نعرفه عن ذرات الهيدروجين العادية التي لا تتفكك. علاوة على ذلك، فإن الحركة الكلاسيكية للإلكترون غير قادرة على تفسير طيف الانبعاث المنفصل للهيدروجين.
للتحايل على هاتين الصعبتين، اقترح بوهر الفرضيات الثلاثة التالية لنموذج بوهر:
- يتحرك الإلكترون السالب حول النواة الموجبة (البروتون) في مدار دائري. تتمركز جميع مدارات الإلكترون في النواة. لا تتوفر جميع المدارات التقليدية الممكنة لإلكترون مرتبط بالنواة.
- تفي مدارات الإلكترون المسموح بها بشرط التحديد الكمي الأول: في المدار n، يمكن للزخم\(L_n\) الزاوي للإلكترون أن يأخذ قيمًا منفصلة فقط: تقول\[L_n = n\hbar, \, where \, n = 1,2,3, . . . \nonumber \] هذه الفرضية أن الزخم الزاوي للإلكترون يتم قياسه كميًا. يُشار\(r_n\) إلى نصف قطر المدار n th وسرعة الإلكترون فيه، على التوالي، ويمكن التعبير عن شرط التكمية الأول بشكل صريح على النحو التالي\(v_n\)\[m_ev_nr_n = n\hbar. \label{6.34} \]
- يُسمح للإلكترون بإجراء انتقالات من مدار حيث توجد طاقته\(E_n\) إلى مدار آخر حيث توجد طاقته\(E_m\). عندما تمتص الذرة الفوتون، ينتقل الإلكترون إلى مدار ذي طاقة أعلى. عندما تصدر ذرة فوتون، ينتقل الإلكترون إلى مدار منخفض الطاقة. تحدث التحولات الإلكترونية مع امتصاص الفوتون المتزامن أو انبعاث الفوتون على الفور. تفي انتقالات الإلكترون المسموح بها بشرط التكميم الثاني:\[hf = |E_n - E_m| \nonumber \] أين\(hf\) توجد طاقة الفوتون المنبعث أو الممتص بتردد\(f\). ينص شرط القياس الكمي الثاني على أن تغيير الإلكترون في الطاقة في ذرة الهيدروجين يتم قياسه كميًا.
تسمح لنا هذه الفرضيات الثلاثة لنظرية الكم المبكرة لذرة الهيدروجين باستخلاص ليس فقط صيغة Rydberg، ولكن أيضًا قيمة ثابت Rydberg والخصائص المهمة الأخرى لذرة الهيدروجين مثل مستويات الطاقة وطاقة التأين وأحجام مدارات الإلكترون. لاحظ أنه في نموذج بور، إلى جانب افتراضين غير كلاسيكيين للتحديد الكمي، لدينا أيضًا الوصف الكلاسيكي للإلكترون كجسيم يتعرض لقوة كولوم، ويجب أن تخضع حركته لقوانين نيوتن للحركة. يجب أن تخضع ذرة الهيدروجين، كنظام معزول، لقوانين الحفاظ على الطاقة والزخم بالطريقة التي نعرفها من الفيزياء الكلاسيكية. مع وضع هذا الإطار النظري في الاعتبار، نحن على استعداد للمضي قدمًا في تحليلنا.
مدارات إلكترون
للحصول على حجم\(r_n\) الإلكترون في المدار وسرعة الإلكترون\(v_n\) فيه، ننتقل إلى الميكانيكا النيوتونية. كجسيم مشحون، يواجه الإلكترون سحبًا إلكتروستاتيكيًا باتجاه النواة المشحونة إيجابًا في مركز مداره الدائري. هذا السحب الكهروستاتيكي هو قوة الجاذبية المركزية التي تجعل الإلكترون يتحرك في دائرة حول النواة. لذلك، يتم تحديد حجم قوة الجذب المركزي بحجم القوة الكهروستاتيكية:
\[ \dfrac{m_ev_n^2}{r_n} = \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{r_n^2}. \label{6.36} \]
هنا\(e\)، تشير إلى قيمة الشحنة الأولية. الإلكترون السالب والبروتون الموجب لهما نفس قيمة الشحنة،
\[|q| = e. \nonumber \]
عندما يتم دمج المعادلة\ ref {6.36} مع شرط القياس الكمي الأول المعطى بالمعادلة\ ref {6.34}، يمكننا حل السرعة\(v_n\)، وبالنسبة لنصف القطر،\(r_n\):
\[v_n = \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{\hbar} \dfrac{1}{n} \label{6.37} \]
\[r_n = 4\pi \epsilon_0 \dfrac{\hbar^2}{m_ee^2}n^2. \label{6.38} \]
لاحظ أن هذه النتائج تخبرنا أن سرعة الإلكترون وكذلك نصف قطر مداره يعتمدان فقط على الفهرس n الذي يعدد المدار لأن جميع الكميات الأخرى في المعادلات السابقة هي ثوابت أساسية. نرى من المعادلة\ ref {6.38} أن حجم المدار ينمو كمربع n. وهذا يعني أن المدار الثاني أكبر بأربعة أضعاف من المدار الأول، والمدار الثالث أكبر بتسعة أضعاف المدار الأول، وهكذا. نرى أيضًا من المعادلة\ ref {6.37} أن سرعة الإلكترون في المدار تتناقص مع زيادة حجم المدار. تكون سرعة الإلكترون أكبر في مدار بوهر الأول\(n = 1\)، حيث إنه المدار الأقرب إلى النواة. يُطلق على نصف قطر مدار بوهر الأول نصف قطر بوهر للهيدروجين، ويُشار إليه بـ\(a_0\). يتم الحصول على قيمتها من خلال الإعداد\(n = 1\) في المعادلة\ ref {6.38}:
\[a_0 = 4\pi \epsilon_0 \dfrac{\hbar^2}{m_ee^2} = 5.29 \times 10^{-11} m = 0.529\space Å. \nonumber \]
يمكننا أن نستبدل\(a_0\) في المعادلة\ ref {6.38} بالتعبير عن نصف قطر المدار n بدلالة\(a_0\):
\[r_n = a_0n^2. \label{6.40} \]
هذه النتيجة تعني أن مدارات الإلكترون في ذرة الهيدروجين يتم قياسها كميًا لأن نصف القطر المداري يأخذ فقط قيمًا محددة\(4a_0\) لـ\(a_0\)\(9a_0\)،،،\(16a_0\)... تُعطى بواسطة المعادلة\ المرجع {6.40}، ولا يُسمح بأي قيم أخرى.
طاقات الإلكترون
الطاقة الكلية\(E_n\) للإلكترون في المدار n هي مجموع طاقته الحركية\(K_n\) وطاقته الكهروستاتيكية الكامنة\(U_n\). باستخدام المعادلة\ ref {6.37}، نجد ذلك
\[K_n = \dfrac{1}{2}m_ev_n^2 = \dfrac{1}{32\pi^2 \epsilon^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.41} \]
تذكر أن طاقة الجهد الكهروستاتيكي للتفاعل\(q_1\) بين شحنتين\(q_2\) والتي تفصل بينها مسافة\(r_{12}\) هي\((1/4\pi \epsilon_0)q_1q_2/r_{12}\). هنا،\(q_1 = +e\) هي شحنة النواة في ذرة الهيدروجين (شحنة البروتون)،\(q_2 = -e\) وهي شحنة الإلكترون\(r_{12} = r_n\) وهي نصف قطر المدار n- th. الآن نستخدم المعادلة\ ref {6.38} لإيجاد الطاقة الكامنة للإلكترون:
\[U_n = - \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{r_n} = - \dfrac{1}{16\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.42} \]
الطاقة الكلية للإلكترون هي مجموع المعادلة\ المرجع {6.41} والمعادلة\ المرجع {6.42}:
\[E_n = K_n + U_n = - \dfrac{1}{32\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.43} \]
لاحظ أن الطاقة تعتمد فقط على الفهرس n لأن الرموز المتبقية في المعادلة\ ref {6.43} هي ثوابت مادية. قيمة العامل الثابت في المعادلة\ ref {6.43} هي
\[E_0 = \dfrac{1}{32\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} = \dfrac{1}{8\epsilon_0^2} \dfrac{m_ee^4}{h^2} = 2.17 \times 10^{-18} J = 13.6 \, eV. \label{6.44} \]
من الملائم التعبير عن طاقة الإلكترون في المدار n من حيث هذه الطاقة، مثل
\[E_n = -E_0 \dfrac{1}{n^2}. \label{6.45} \]
يمكننا الآن أن نرى أن طاقات الإلكترون في ذرة الهيدروجين يتم قياسها كميًا لأنها يمكن أن تحتوي فقط على قيم منفصلة\(-E_0, \, -E_0/4, \, -E_0/9, \, -E_0/16, . . . \) تُعطى بواسطة المعادلة\ ref {6.45}، ولا يُسمح بقيم طاقة أخرى. تسمى هذه المجموعة من الطاقات الإلكترونية المسموح بها طيف الطاقة للهيدروجين (الشكل\(\PageIndex{5}\)). يُطلق على المؤشر n الذي يعدد مستويات الطاقة في نموذج Bohr الرقم الكمي للطاقة. نحدد طاقة الإلكترون داخل ذرة الهيدروجين مع طاقة ذرة الهيدروجين. لاحظ أنه يتم الحصول على أصغر قيمة للطاقة\(n = 1\)، لذلك لا يمكن أن تحتوي ذرة الهيدروجين على طاقة أصغر من ذلك. تسمى هذه القيمة الأصغر لطاقة الإلكترون في ذرة الهيدروجين طاقة الحالة الأرضية لذرة الهيدروجين وقيمتها هي
\[E_1 = −E_0 = −13.6 \, eV. \label{6.46} \]
قد تحتوي ذرة الهيدروجين على طاقات أخرى أعلى من الحالة الأرضية. تُعرف حالات الطاقة العالية هذه بحالات الطاقة المثيرة لذرة الهيدروجين.
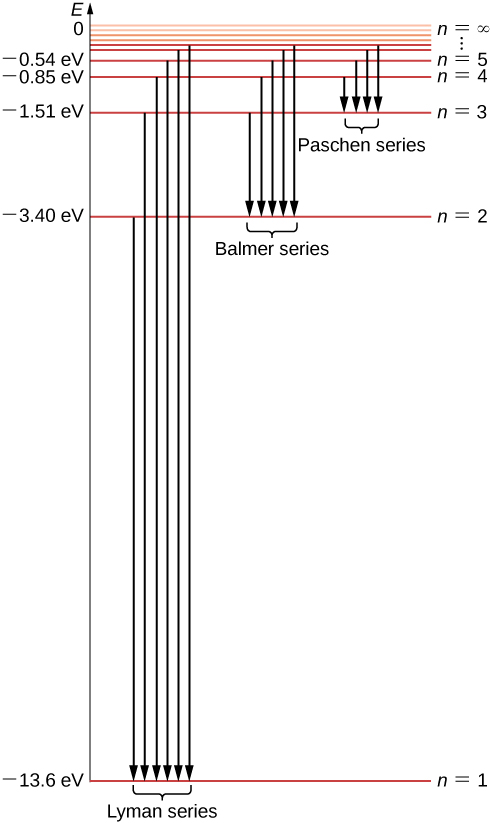
هناك حالة أرضية واحدة فقط، ولكن هناك عدد لا نهائي من الحالات المثيرة نظرًا لوجود عدد لا نهائي من قيم n في المعادلة\ ref {6.45}. نقول أن الإلكترون يكون في «حالة الخروج الأولى» عندما تكون طاقته\(E_n\) (عندما\(n = 2\))، وهي الحالة المثيرة الثانية عندما تكون طاقته\(E_3\) (عندما\(n = 3\))، وبشكل عام، في الحالة n الموجودة عندما تكون طاقته\(E_n + 1\). لا توجد حالة حماسية على الإطلاق؛ ومع ذلك، هناك حد لتسلسل الحالات المثيرة. إذا واصلنا الزيادة\(n\) في المعادلة\ ref {6.45}، نجد أن الحد هو\(- lim_{n \rightarrow \infty} \, E_0/n^2 = 0\). في هذا الحد، لم يعد الإلكترون مرتبطًا بالنواة بل يصبح إلكترونًا حرًا. يظل الإلكترون مرتبطًا بذرة الهيدروجين طالما كانت طاقته سالبة. الإلكترون الذي يدور حول النواة في مدار بوهر الأول، الأقرب إلى النواة، يكون في حالة الأرض، حيث تكون لطاقته أصغر قيمة. في الحالة الأرضية، يرتبط الإلكترون بقوة بالنواة ويتم إعطاء طاقته من خلال المعادلة\ ref {6.46}. إذا أردنا إزالة هذا الإلكترون من الذرة، يجب علينا تزويده بالطاقة الكافية\(E_{\infty}\)، لموازنة طاقة حالته الأرضية على الأقل\(E_1\):
\[E_{\infty} + E_1 = 0 \Rightarrow E_{\infty} = - E_1 = - (- E_0) = E_0 = 13.6 \, eV. \label{6.47} \]
الطاقة اللازمة لإزالة الإلكترون من الذرة تسمى طاقة التأين. تسمى طاقة\(E_{\infty}\) التأين اللازمة لإزالة الإلكترون من مدار بوهر الأول حد التأين لذرة الهيدروجين. حد التأين في المعادلة\ ref {6.47} الذي نحصل عليه في نموذج Bohr يتفق مع القيمة التجريبية.
خطوط الانبعاث الطيفي للهيدروجين
للحصول على الأطوال الموجية للإشعاع المنبعث عندما ينتقل الإلكترون من المدار n- th إلى المدار m، نستخدم ثاني شروط التكمية الخاصة بـ Bohr والمعادلة\ ref {6.45} للطاقات. يمكن أن يحدث انبعاث الطاقة من الذرة فقط عندما ينتقل الإلكترون من حالة الإثارة إلى حالة الطاقة المنخفضة. في سياق هذا التحول، يزيل الفوتون المنبعث فرق الطاقات بين الدول المشاركة في الانتقال. لا يمكن أن يسير الانتقال في الاتجاه الآخر لأن طاقة الفوتون لا يمكن أن تكون سالبة، مما يعني أنه بالنسبة للانبعاثات يجب أن يكون لدينا\(E_n > E_m\) و\(n > m\). لذلك، يعطي الجزء الثالث من افتراضات بوهر
\[\begin{align} hf &= |E_n - E_m| \nonumber \\[4pt] &= E_n - E_m \nonumber \\[4pt] &= -E_0 \dfrac{1}{n^2} + E_m \dfrac{1}{m^2} \nonumber \\[4pt] &= E_0 \left( \dfrac{1}{m^2} - \dfrac{1}{n^2} \right). \label{6.48} \end{align} \]
نعبر الآن عن طاقة الفوتون من حيث طوله الموجي\(hf = hc/\lambda\)، ونقسم طرفي المعادلة\ ref {6.48} على\(hc\). النتيجة هي
\[ \dfrac{1}{\lambda} = \dfrac{E_0}{hc} \left( \dfrac{1}{m^2} - \dfrac{1}{n^2} \right). \label{6.49} \]
قيمة الثابت في هذه المعادلة هي
\[\dfrac{E_0}{hc} = \dfrac{13.6 \, eV}{(4.136 \times 10^{-15} eV \cdot s)(2.997 \times 10^8 m/s)} = 1.097 \times 10^7 \dfrac{1}{m}. \label{6.50} \]
هذه القيمة هي بالضبط ثابت Rydberg\(R_H\) في معادلة صيغة Rydberg الاستدلالية\ ref {rydberg}. في الواقع، المعادلة\ ref {6.49} مطابقة لصيغة Rydberg، لأنه بالنسبة لـ m معين، لدينا\(n = m + 1, \, m + 2, . . .\). بهذه الطريقة، يسمح لنا نموذج Bohr الكمي لذرة الهيدروجين باستخلاص ثابت Rydberg التجريبي من المبادئ الأولى والتعبير عنه من حيث الثوابت الأساسية. يوضح الشكل التحولات بين مدارات الإلكترون المسموح بها\(\PageIndex{5}\).
يمكننا تكرار نفس الخطوات التي أدت إلى المعادلة\ ref {6.49} للحصول على الطول الموجي للإشعاع الممتص؛ وهذا يعطي مرة أخرى المعادلة\ ref {6.49} ولكن هذه المرة لمواقع خطوط الامتصاص في طيف امتصاص الهيدروجين. والفرق الوحيد هو أنه بالنسبة للامتصاص، فإن الرقم الكمي\(m\) هو مؤشر المدار الذي يشغله الإلكترون قبل الانتقال (مدار الطاقة المنخفضة) والرقم الكمي\(n\) هو مؤشر المدار الذي ينتقل إليه الإلكترون (مدار الطاقة العالية). الفرق بين طاقات الإلكترون في هذين المدارين هو طاقة الفوتون الممتص.
إذا كانت ذرة الهيدروجين في الحالة الأرضية تمتص فوتون 93.7 نانومتر، المقابل لخط انتقالي في سلسلة ليمان، فكيف يؤثر ذلك على طاقة الذرة وحجمها؟ ما مقدار الطاقة اللازمة لتأين الذرة عندما تكون في هذه الحالة المثيرة؟ قدم إجاباتك بوحدات مطلقة، وبنسبة إلى الحالة الأرضية.
إستراتيجية
قبل الامتصاص، تكون الذرة في حالتها الأرضية. هذا يعني أن انتقال الإلكترون يحدث من المدار\(m = 1\) إلى بعض المستويات الأعلى في المدار. أولاً، يجب علينا تحديد nn للطول الموجي الممتص\(\lambda = 93.7 \, nm\). بعد ذلك، يمكننا استخدام المعادلة\ ref {6.45} لإيجاد طاقة\(E_n\) الحالة المثارة وطاقة التأين الخاصة بها\(E_{\infty,n}\)، واستخدام المعادلة\ ref {6.40} لإيجاد نصف قطر\(r_n\) الذرة في الحالة المثارة. لتقدير n، نستخدم المعادلة\ ref {6.49}.
الحل
استبدل\(m = 1\) و = 93.7 nm في المعادلة\ ref {6.49} وقم بحل n. يجب ألا تتوقع الحصول على إجابة صحيحة مثالية بسبب أخطاء التقريب، ولكن إجابتك ستكون قريبة من عدد صحيح، ويمكنك تقدير n بأخذ الجزء المتكامل من إجابتك:
\[ \begin{align*} \dfrac{1}{\lambda} &= R_H \left( \dfrac{1}{1^1} - \dfrac{1}{n^2}\right) \\[4pt] \Rightarrow n &= \dfrac{1}{\sqrt{1 - \dfrac{1}{\lambda R_H}}} \\[4pt] &= \dfrac{1}{\sqrt{1 - \dfrac{1}{(93.7 \times 10^{−9}m)(1.097 \times 10^7 m^{−1})}}} \\[4pt] &= 6.07 \\[4pt] \Rightarrow n &= 6. \end{align*} \]
نصف قطر\(n = 6\) المدار هو
\[r_n = a_0n^2= a_06^2 = 36a_0 = 36(0.529 \times 10^{−10} \, m) = 19.04 \times 10^{−10}\space m ≅ 19.0 \, Å. \nonumber \]
وهكذا، بعد امتصاص الفوتون 93.7 نانومتر، يكون حجم ذرة الهيدروجين في\(n = 6\) الحالة المثارة أكبر 36 مرة مما كان عليه قبل الامتصاص، عندما كانت الذرة في الحالة الأرضية. طاقة الدولة الحماسية الخامسة (\(n = 6\)) هي:
\[E_n = - \dfrac{E_0}{n^2} = - \dfrac{E_0}{6^2} = - \dfrac{E_0}{36} = - \dfrac{13.6 \, eV}{36} ≅ − 0.378 \, eV. \nonumber \]
بعد امتصاص الفوتون البالغ 93.7 نانومتر، تكون طاقة ذرة الهيدروجين أكبر مما كانت عليه قبل الامتصاص. يتطلب تأين الذرة عندما تكون في الحالة المثارة الخامسة (\(n = 6\)) طاقة أقل بمقدار 36 مرة مما هو مطلوب عندما تكون الذرة في الحالة الأرضية:
\[E_{\infty,6} = -E_6 = -(-0.378 \, eV) = 0.378 \, eV. \nonumber \]
الدلالة
يمكننا تحليل أي خط طيفي في طيف الهيدروجين بنفس الطريقة. وبالتالي، فإن القياسات التجريبية للخطوط الطيفية تزودنا بمعلومات حول البنية الذرية لذرة الهيدروجين.
عندما يكون إلكترون في ذرة هيدروجين في حالة الإثارة الأولى، ما التنبؤ الذي يقدمه نموذج بوهر بشأن سرعته المدارية وطاقته الحركية؟ ما مقدار الزخم الزاوي المداري؟
- إجابة
-
\(v_2 = 1.1 \times 10^6 m/s ≅0.0036 \, c;\)
\(L_2 = 2\hbar K_2 = 3.4 \, eV\)
يتنبأ نموذج Bohr لذرة الهيدروجين أيضًا بشكل صحيح بأطياف بعض الأيونات الشبيهة بالهيدروجين. الأيونات الشبيهة بالهيدروجين هي ذرات عناصر ذات رقم ذري Z أكبر من واحد (\(Z = 1\)للهيدروجين) ولكن مع إزالة جميع الإلكترونات باستثناء واحد. على سبيل المثال، تحتوي ذرة الهيليوم المحايدة كهربائيًا على عدد ذري\(Z = 2\). هذا يعني أنه يحتوي على إلكترونين يدوران حول النواة بشحنة قدرها\(q = +Ze\). عندما تتم إزالة أحد الإلكترونات المدارية من ذرة الهيليوم (نقول، عندما تتأين ذرة الهيليوم بشكل فردي)، فإن ما يتبقى هو بنية ذرية تشبه الهيدروجين حيث يدور الإلكترون المتبقي حول النواة بشحنة قدرها\(q = +Ze\). يتم وصف هذا النوع من المواقف بنموذج Bohr. بافتراض أن شحنة النواة ليست كذلك\(+Ze\)،\(+e\) يمكننا تكرار جميع الخطوات، بدءًا من المعادلة\ ref {6.36}، للحصول على نتائج أيون يشبه الهيدروجين:
\[r_n = \dfrac{a_0}{Z}n^2 \label{6.51} \]
أين\(a_0\) هو مدار بوهر للهيدروجين، و
\[E_n = -Z^2E_0 \dfrac{1}{n^2} \label{6.52} \]
أين\(E_0\) هو حد التأين لذرة الهيدروجين. هذه المعادلات تقريبية جيدة طالما أن الرقم الذري Z ليس كبيرًا جدًا.
يعد نموذج Bohr مهمًا لأنه كان أول نموذج يفترض تحديد كمية مدارات الإلكترون في الذرات. وبالتالي، فهي تمثل نظرية الكم المبكرة التي أعطت بداية لتطوير نظرية الكم الحديثة. قدم مفهوم الرقم الكمي لوصف الحالات الذرية. تكمن قيود نظرية الكم المبكرة في أنها لا تستطيع وصف الذرات التي يكون فيها عدد الإلكترونات التي تدور حول النواة أكبر من واحد. نموذج Bohr للهيدروجين هو نموذج شبه كلاسيكي لأنه يجمع بين المفهوم الكلاسيكي لمدارات الإلكترون والمفهوم الجديد للتحديد الكمي. دفع النجاح الملحوظ لهذا النموذج العديد من علماء الفيزياء إلى البحث عن تفسير لماذا يجب أن يعمل هذا النموذج على الإطلاق، والسعي لفهم الفيزياء وراء افتراضات نظرية الكم المبكرة. أدى هذا البحث إلى بداية مفهوم جديد تمامًا لـ «موجات المادة».


