4.6: الفتحات الدائرية والقرار
- Page ID
- 196550
في نهاية هذا القسم، ستكون قادرًا على:
- وصف حد الحيود عند الدقة
- وصف حد الحيود عند انتشار الشعاع
ينحرف الضوء أثناء تحركه عبر الفضاء، وينحني حول العقبات، ويتدخل بشكل بناء ومدمر. يمكن استخدام هذا كأداة طيفية - يشتت محزوز الحيود الضوء وفقًا لطول الموجة، على سبيل المثال، ويستخدم لإنتاج الطيف - ولكن الحيود يحد أيضًا من التفاصيل التي يمكننا الحصول عليها في الصور.
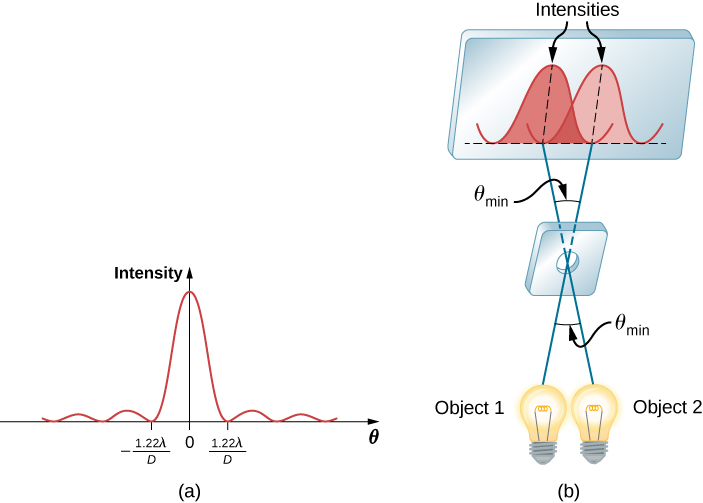
\(\PageIndex{1a}\)يوضح الشكل تأثير تمرير الضوء من خلال فتحة دائرية صغيرة. بدلاً من النقطة المضيئة ذات الحواف الحادة، نحصل على بقعة ذات حافة غامضة محاطة بدوائر من الضوء. يحدث هذا النمط بسبب الحيود، على غرار ذلك الناتج عن شق واحد. يتداخل الضوء من أجزاء مختلفة من الفتحة الدائرية بشكل بناء ومدمر. يكون التأثير أكثر وضوحًا عندما تكون الفتحة صغيرة، ولكن التأثير يكون موجودًا للفتحات الكبيرة أيضًا.

كيف يؤثر الحيود على التفاصيل التي يمكن ملاحظتها عندما يمر الضوء عبر الفتحة؟ \(\PageIndex{1b}\)يوضح الشكل نمط الحيود الناتج عن مصدري ضوء نقطي قريبين من بعضهما البعض. يشبه النمط ذلك الخاص بمصدر نقطة واحدة، ولا يزال من الممكن معرفة أن هناك مصدرين للضوء بدلاً من مصدر واحد. إذا كانوا أقرب إلى بعضهم البعض، كما هو الحال في الشكل\(\PageIndex{1c}\)، لا يمكننا التمييز بينهما، وبالتالي الحد من التفاصيل أو الدقة التي يمكننا الحصول عليها. هذا الحد هو نتيجة لا مفر منها لطبيعة موجة الضوء.
يحد الانحراف من الدقة في العديد من المواقف. إن حدة رؤيتنا محدودة لأن الضوء يمر عبر حدقة العين، وهي الفتحة الدائرية للعين. انتبه إلى أن انتشار الضوء الشبيه بالحيود يرجع إلى القطر المحدود لشعاع الضوء، وليس التفاعل مع الفتحة. وبالتالي،\(D\) يُظهر الضوء الذي يمر عبر عدسة ذات قطر هذا التأثير وينتشر، مما يؤدي إلى تشويش الصورة، تمامًا كما يحدث الضوء الذي يمر عبر فتحة قطرها\(D\). وبالتالي، فإن الحيود يحد من دقة أي نظام يحتوي على عدسة أو مرآة. التلسكوبات محدودة أيضًا بسبب الحيود، بسبب القطر\(D\) المحدود للمرآة الأولية.
فقط ما هو الحد؟ للإجابة على هذا السؤال، ضع في اعتبارك نمط الحيود للفتحة الدائرية، التي لها حد أقصى مركزي أوسع وأكثر سطوعًا من الحد الأقصى المحيط بها (على غرار الشق) (الشكل\(\PageIndex{1a}\)). يمكن إثبات أنه بالنسبة للفتحة الدائرية ذات القطر\(D\)، يحدث الحد الأدنى الأول في نمط الحيود عند\(\theta = 1.22 \lambda/D\) (بشرط أن تكون الفتحة كبيرة مقارنة بالطول الموجي للضوء، وهو الحال بالنسبة لمعظم الأدوات البصرية). يُعرف المعيار المقبول لتحديد حد الحيود للقرار بناءً على هذه الزاوية بمعيار Rayleigh، الذي طوره اللورد Rayleigh في القرن التاسع عشر.
ينص حد الحيود للدقة على أن صورتين يمكن حلهما فقط عندما يكون مركز نمط الحيود لأحدهما أعلى مباشرة من الحد الأدنى الأول لنمط الحيود للأخرى (الشكل\(\PageIndex{1b}\)).
الحد الأدنى الأول يكون بزاوية\(\theta = 1.22 \lambda/D\)، بحيث يمكن حل كائنين من نقطتين فقط إذا تم فصلهما بالزاوية
\[\theta = 1.22 \dfrac{\lambda}{D} \label{Rayleigh} \]
أين\(λ\) هو الطول الموجي للضوء (أو أي إشعاع كهرومغناطيسي آخر)\(D\) وهو قطر الفتحة والعدسة والمرآة وما إلى ذلك، والتي يتم بها ملاحظة الجسمين. في هذا التعبير،\(θ\) يحتوي على وحدات من الراديان. تُعرف هذه الزاوية أيضًا باسم حد الحيود.
جميع محاولات مراقبة حجم وشكل الأجسام محدودة بطول موجة المسبار. حتى الطول الموجي الصغير للضوء يمنع الدقة الدقيقة. عند استخدام مجسات ذات طول موجي صغير للغاية، كما هو الحال مع المجهر الإلكتروني، يكون النظام مضطربًا، مما لا يزال يحد من معرفتنا. يؤكد مبدأ عدم اليقين لهايزنبرغ أن هذا الحد أساسي ولا مفر منه، كما سنرى في الفصل الخاص بميكانيكا الكم.
يبلغ قطر المرآة الرئيسية لتلسكوب هابل الفضائي المداري 2.40 مترًا، ويؤدي وجود هذا التلسكوب في المدار إلى تجنب الآثار المهينة لتشويه الغلاف الجوي على استقراره. (أ) ما هي الزاوية بين مصدري ضوء نقطيين قابلين للحل فقط (ربما نجمتان)؟ افترض أن متوسط الطول الموجي للضوء يبلغ 550 nm. (ب) إذا كان هذان النجمان على مسافة مليوني سنة ضوئية، وهي مسافة مجرة أندروميدا، فما مدى قربهما من بعضهما البعض وما زال بالإمكان حلهما؟ (السنة الضوئية، أو الطيران، هي المسافة التي يقطعها الضوء في عام واحد.)
إستراتيجية
يعطي معيار Rayleigh المذكور في Equation\ ref {Rayleigh}\(\theta = 1.22 \lambda/D\)، أصغر زاوية ممكنة بين مصادر النقاط، أو أفضل دقة يمكن الحصول عليها. بمجرد معرفة هذه الزاوية، يمكننا حساب المسافة بين النجوم، حيث يتم إعطاؤنا مدى بعدهم.
الحل
- معيار Rayleigh للحد الأدنى للزاوية القابلة للحل هو\[\theta = 1.22 \dfrac{\lambda}{D}. \nonumber \] إدخال القيم المعروفة\[\theta = 1.22\dfrac{550 \times 10^{-9} m}{2.40 \,m} = 2.80 \times 10^{-7} rad. \nonumber \]
- المسافة بين جسمين على بعد أو مسافة أو بينهما وزاوية تساوي\(s = r\theta\). يعطي استبدال القيم المعروفة\[s = (2.0 \times 10^6 \,ly)(2.80 \times 10^{-7} \,rad) = 0.56 \,ly. \nonumber \]
الدلالة
الزاوية الموجودة في الجزء (أ) صغيرة للغاية (أقل من 1/50,000 درجة)، لأن المرآة الأولية كبيرة جدًا مقارنة بالطول الموجي للضوء. كما لوحظ، تكون تأثيرات الحيود أكثر وضوحًا عندما يتفاعل الضوء مع الأجسام ذات الأحجام بترتيب الطول الموجي للضوء. ومع ذلك، لا يزال التأثير موجودًا، وهناك حد الحيود لما يمكن ملاحظته. الدقة الفعلية لتلسكوب هابل ليست جيدة تمامًا كما هو موجود هنا. كما هو الحال مع جميع الأدوات، هناك تأثيرات أخرى، مثل عدم التماثل في المرايا أو الانحرافات في العدسات التي تزيد من الحد من الدقة. ومع ذلك، يشير الشكل\(\PageIndex{3}\) إلى مدى التفاصيل التي يمكن ملاحظتها مع هابل بسبب حجمها وجودتها، وخاصة لأنها فوق الغلاف الجوي للأرض.

تشير الإجابة في الجزء (ب) إلى أنه يمكن حل نجمتين يفصل بينهما حوالي نصف سنة ضوئية. يبلغ متوسط المسافة بين النجوم في المجرة حوالي خمس سنوات ضوئية في الأجزاء الخارجية وحوالي سنة ضوئية واحدة بالقرب من مركز المجرة. لذلك، يمكن لهابل حل معظم النجوم الفردية في مجرة أندروميدا، على الرغم من أنها تقع على مسافة كبيرة بحيث يستغرق ضوءها مليوني سنة للوصول إلينا. \(\PageIndex{4}\)يوضح الشكل مرآة أخرى تستخدم لمراقبة موجات الراديو من الفضاء الخارجي.

ما الدقة الزاوية لتلسكوب أريسيبو الموضَّحة في الشكل\(\PageIndex{4}\) عند تشغيله بطول موجي يبلغ ٢١ سم؟ كيف يمكن مقارنتها بدقة تلسكوب هابل؟
- إجابة
-
\(8.4 \times 10^{-4} \,rad\)، أوسع بـ 3000 مرة من تلسكوب هابل
لا يمثل الحيود مشكلة للأجهزة البصرية فحسب، بل يمثل أيضًا الإشعاع الكهرومغناطيسي نفسه. يُظهر أي شعاع ضوئي له قطر محدود\(D\) وطول موجة انتشار الحيود. ينتشر الشعاع بزاوية معطاة بالمعادلة\ ref {Rayleigh}،\(\theta = 1.22 \lambda/D\). خذ، على سبيل المثال، شعاع ليزر مصنوع من أشعة متوازية قدر الإمكان (زوايا بين الأشعة قريبة من = 0 درجة قدر الإمكان) بدلاً من ذلك ينتشر بزاوية\(\theta = 1.22 \lambda/D\)، حيث\(D\) يكون قطر الشعاع و هو طوله الموجي. من المستحيل ملاحظة هذا الانتشار للمصباح لأن شعاعه ليس متوازيًا جدًا في البداية. ومع ذلك، بالنسبة للإرسال لمسافات طويلة لأشعة الليزر أو إشارات الميكروويف، يمكن أن يكون انتشار الحيود كبيرًا (الشكل\(\PageIndex{5}\)). لتجنب ذلك، يمكننا زيادة D. يتم ذلك لضوء الليزر المرسل إلى القمر لقياس المسافة من الأرض. يتم توسيع شعاع الليزر من خلال التلسكوب ليصبح أكبر\(D\) بكثير وأصغر.
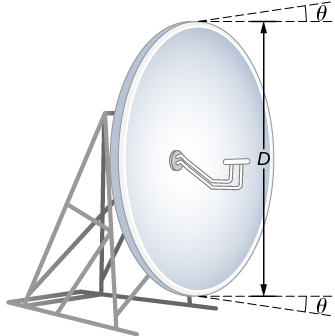
في معظم مختبرات علم الأحياء، تكون الدقة مشكلة عند إدخال استخدام المجهر. كلما كانت المسافة x أصغر التي يمكن من خلالها فصل كائنين والاستمرار في النظر إليهما على أنهما مميزان، زادت الدقة. يتم تعريف قوة حل العدسة على أنها تلك المسافة x. يتم الحصول على تعبير لحل القوة من معيار Rayleigh. \(\PageIndex{6a}\)يوضح الشكل كائنين نقطيين يفصل بينهما مسافة x. وفقًا لمعيار Rayleigh، تكون الدقة ممكنة عندما يكون الحد الأدنى للفصل الزاوي
\[\theta = 1.22 \dfrac{\lambda}{D} = \dfrac{x}{d}, \nonumber \]
أين\(D\) هي المسافة بين العينة والعدسة الموضوعية، وقد استخدمنا تقريب الزاوية الصغيرة (أي أننا افترضنا أن x أصغر بكثير من d)، لذلك\(tan \,\theta \approx sin \,\theta\). لذلك، فإن قوة الحل هي
\[x= 1.22 \dfrac{\lambda d}{D}. \nonumber \]
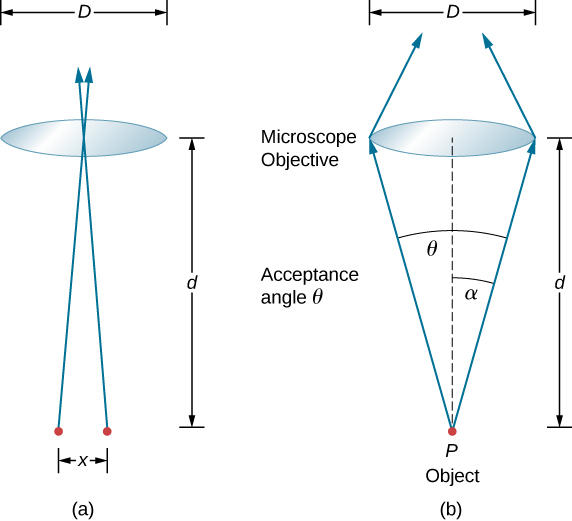
هناك طريقة أخرى للنظر إلى هذا من خلال مفهوم الفتحة العددية (NA)، وهي مقياس لزاوية القبول القصوى التي تلتقط فيها العدسة الضوء وتظل تحتويه داخل العدسة. \(\PageIndex{1b}\)يوضح الشكل عدسة وكائن عند النقطة P. يعد NA هنا مقياسًا لقدرة العدسة على جمع الضوء وحل التفاصيل الدقيقة. يتم تعريف الزاوية الفرعية للعدسة عند تركيزها على أنها\(\theta = 2\alpha\). من الشكل ومرة أخرى باستخدام تقريب الزاوية الصغيرة، يمكننا الكتابة
\[sin \,\alpha = \dfrac{D/2}{d} = \dfrac{D}{2d}. \nonumber \]
إن NA للعدسة هو\(NA = n \,sin \,\alpha\)، حيث n هو معامل انكسار الوسط بين العدسة الشيئية والجسم عند النقطة P. من هذا التعريف لـ NA، يمكننا أن نرى ذلك
\[x = 1.22 \dfrac{\lambda d}{D} = 1.22 \dfrac{\lambda}{2 \,sin \,\alpha} = 0.61 \dfrac{\lambda n}{NA}. \nonumber \]
في المجهر، يعد الحمض النووي مهمًا لأنه يتعلق بقدرة حل العدسة. العدسة ذات NA الكبير قادرة على حل التفاصيل الدقيقة. العدسات ذات NA الأكبر قادرة أيضًا على جمع المزيد من الضوء وبالتالي إعطاء صورة أكثر إشراقًا. هناك طريقة أخرى لوصف هذا الموقف وهي أنه كلما كبر NA، زاد مخروط الضوء الذي يمكن إدخاله إلى العدسة، لذلك يتم جمع المزيد من أنماط الحيود. وبالتالي فإن المجهر يحتوي على مزيد من المعلومات لتشكيل صورة واضحة، وقوة حله أعلى.
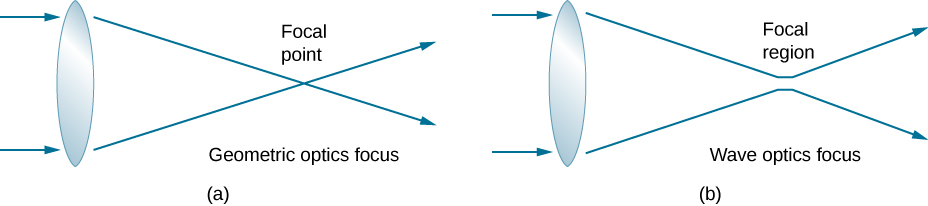
تتمثل إحدى عواقب الحيود في أن النقطة المحورية للحزمة لها عرض محدود وتوزيع كثافة. تخيل التركيز عند التفكير فقط في البصريات الهندسية، كما في الشكل\(\PageIndex{7a}\). تعتبر النقطة البؤرية نقطة صغيرة للغاية ذات كثافة هائلة وقدرة على حرق معظم العينات، بغض النظر عن الحمض النووي للعدسة الموضوعية - وهو تبسيط مفرط غير مادي. بالنسبة للبصريات الموجية، بسبب الحيود، نأخذ في الاعتبار الظاهرة التي تنتشر فيها النقطة البؤرية لتصبح نقطة محورية (الشكل\(\PageIndex{7b}\)) مع انخفاض حجم البقعة مع زيادة NA. وبالتالي، تزداد الكثافة في النقطة البؤرية مع زيادة NA. كلما ارتفع الحمض النووي، زادت فرص التحلل الضوئي للعينة. ومع ذلك، لا تصبح البقعة أبدًا نقطة حقيقية.
في نوع مختلف من الميكروسكوب، تُصنع الجزيئات داخل العينة لإصدار الضوء من خلال آلية تسمى الفلورة. من خلال التحكم في الجزيئات التي تنبعث منها الضوء، أصبح من الممكن إنشاء صور بدقة أدق بكثير من معيار Rayleigh، وبالتالي التحايل على حد الحيود. أدى تطوير الفحص المجهري الفلوري فائق الدقة إلى جائزة نوبل في الكيمياء لعام 2014.
في نموذج الدقة الضوئية هذا، يتم عرض نمطين من حيود الضوء من خلال فتحتين دائريتين جنبًا إلى جنب في هذه المحاكاة بواسطة Fu-Kwun Hwang. شاهد الأنماط تندمج أثناء تقليل أقطار الفتحة.


