4.7: حيود الأشعة السينية
- Page ID
- 196581
في نهاية هذا القسم، ستكون قادرًا على:
- وصف تأثيرات التداخل والانحراج التي تظهرها الأشعة السينية عند التفاعل مع الهياكل ذات المقياس الذري
نظرًا لأن فوتونات الأشعة السينية نشطة جدًا، فإن لها أطوال موجية قصيرة نسبيًا تتراوح من\(10^{-8}\) متر إلى\(10^{-12}\) متر، وبالتالي، تعمل فوتونات الأشعة السينية النموذجية مثل الأشعة عندما تواجه أجسامًا مجهرية، مثل الأسنان، وتنتج ظلالًا حادة. ومع ذلك، نظرًا لأن الذرات في حدود 0.1 نانومتر في الحجم، يمكن استخدام الأشعة السينية للكشف عن موقع الذرات والجزيئات وشكلها وحجمها. تسمى هذه العملية حيود الأشعة السينية، وتنطوي على تداخل الأشعة السينية لإنتاج أنماط يمكن تحليلها للحصول على معلومات حول الهياكل التي تشتت الأشعة السينية.
ولعل أشهر مثال على حيود الأشعة السينية هو اكتشاف البنية الحلزونية المزدوجة للحمض النووي في عام 1953 من قبل فريق دولي من العلماء العاملين في مختبر كافنديش في إنجلترا - الأمريكي جيمس واتسون، والإنجليزي فرانسيس كريك، وموريس ويلكينز المولود في نيوزيلندا. باستخدام بيانات حيود الأشعة السينية التي أنتجتها روزاليند فرانكلين، كانوا أول من قام بنمذجة بنية اللولب المزدوج للحمض النووي التي تعتبر بالغة الأهمية للحياة. لهذا العمل، حصل واتسون وكريك وويلكينز على جائزة نوبل لعام 1962 في علم وظائف الأعضاء أو الطب. (هناك بعض الجدل والجدل حول قضية عدم إدراج روزاليند فرانكلين في الجائزة، على الرغم من وفاتها في عام 1958، قبل منح الجائزة.)
\(\PageIndex{1}\)يوضح الشكل نمط الحيود الناتج عن تشتت الأشعة السينية من البلورة. تُعرف هذه العملية باسم علم البلورات بالأشعة السينية بسبب المعلومات التي يمكن أن تقدمها عن التركيب البلوري، وكان هذا هو نوع البيانات التي قدمتها روزاليند فرانكلين إلى واتسون وكريك للحصول على الحمض النووي. لا تؤكد الأشعة السينية حجم وشكل الذرات فحسب، بل تقدم معلومات حول الترتيبات الذرية في المواد. على سبيل المثال، تتضمن الأبحاث الحديثة في الموصلات الفائقة ذات درجة الحرارة العالية مواد معقدة تعتبر ترتيباتها الشبكية ضرورية للحصول على مادة فائقة التوصيل. يمكن دراستها باستخدام علم البلورات بالأشعة السينية.

تاريخيًا، تم استخدام تشتت الأشعة السينية من البلورات لإثبات أن الأشعة السينية هي موجات كهرومغناطيسية نشطة (EM). تم الاشتباه في ذلك منذ اكتشاف الأشعة السينية في عام 1895، ولكن لم يقنع الألماني ماكس فون لاو (1879-1960) اثنين من زملائه بتفريق الأشعة السينية من البلورات حتى عام 1912. إذا تم الحصول على نمط الحيود، فقد استنتج أن الأشعة السينية يجب أن تكون موجات، ويمكن تحديد طولها الموجي. (كان تباعد الذرات في البلورات المختلفة معروفًا بشكل معقول في ذلك الوقت، استنادًا إلى القيم الجيدة لرقم Avogadro.) كانت التجارب مقنعة، وتم منح جائزة نوبل في الفيزياء لعام 1914 لفون لاو لاقتراحه الذي أدى إلى إثبات أن الأشعة السينية هي موجات EM. في عام 1915، حصل فريق الأب والابن الفريد من السير ويليام هنري براغ وابنه السير ويليام لورانس براغ على جائزة نوبل المشتركة لاختراعهم مطياف الأشعة السينية وعلم تحليل الأشعة السينية الجديد آنذاك.
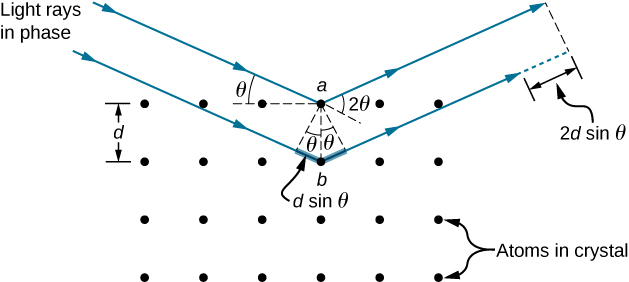
بطرق تذكرنا بتداخل الأغشية الرقيقة، ننظر إلى موجتين مستويتين بأطوال موجية للأشعة السينية، تعكس كل واحدة منهما مستوى مختلفًا من الذرات داخل شبكة البلورة، كما هو موضح في الشكل\(\PageIndex{2}\). من الناحية الهندسية، يكون الفرق في أطوال المسارات هو\(2d \, \sin \, \theta\). ينتج التداخل البنائي عندما تكون هذه المسافة عددًا صحيحًا مضاعفًا لطول الموجة. يتم التقاط هذه الحالة من خلال معادلة Bragg،
\[m\lambda = 2d \, \sin \, \theta,\label{Bragg} \]
من أجل\(m = 1,2,3, ...\).
أين\(m\) يوجد عدد صحيح موجب\(d\) وهو التباعد بين المستويات. وفقًا لقانون الانعكاس، يتم وصف كل من الموجات الساقطة والموجات المنعكسة بنفس الزاوية\(θ\)، ولكن على عكس الممارسة العامة في البصريات الهندسية،\(θ\) يتم قياسها فيما يتعلق بالسطح نفسه، وليس الطبيعي.
يتكون ملح الطعام الشائع بشكل أساسي من\(\ce{NaCl}\) البلورات. في\(\ce{NaCl}\) البلورة، توجد عائلة من الطائرات تفصل بينها مسافة 0.252 نانومتر. إذا لوحظ الحد الأقصى من الدرجة الأولى بزاوية سقوط مقدارها 18.1 درجة، فما الطول الموجي لتشتت الأشعة السينية من هذه البلورة؟
الإستراتيجية:
استخدم معادلة براغ، المعادلة\ ref {Bragg}، لحلها\(θ\).
الحل
بالنسبة للترتيب الأول\(m = 1\)،\(d\) يكون تباعد المستويات معروفًا. حل معادلة Bragg لعوائد الطول الموجي
\[\begin{align*} \lambda &= \dfrac{2d \, \sin \, \theta}{m} \\[4pt] &= \dfrac{2(0.252 \times 10^{-9} m) \, \sin \, (18.1^o)}{1} \\[4pt] &= 1.57 \times 10^{-10} m, \, or \, 0.157 \, nm \end{align*} \nonumber \]
الدلالة
يتناسب الطول الموجي المحدد مع منطقة الأشعة السينية للطيف الكهرومغناطيسي. مرة أخرى، تبرز الطبيعة الموجية للضوء عندما يكون الطول الموجي (\(\lambda = 0.157 \, nm\)) قابلاً للمقارنة بحجم الهياكل المادية (\(d = 0.252 \, nm\)) التي يتفاعل معها.
بالنسبة للتجربة الموضحة في المثال\(\PageIndex{1}\)، ما الزاويتان الأخريان اللتان يمكن ملاحظة الحد الأقصى للتداخل فيهما؟ ما الذي يحد من عدد الحد الأقصى؟
- إجابة
-
\(38.4^o\)و\(68.8^o\)؛ بين\(\theta = 0^o \rightarrow 90^o\) الأوامر 1 و 2 و 3، هي كل ما هو موجود.
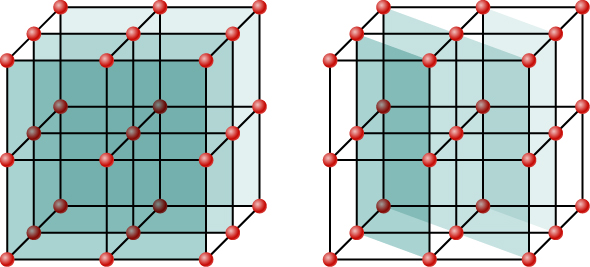
على الرغم من أن الشكل\(\PageIndex{2}\) يصور البلورة كمصفوفة ثنائية الأبعاد من مراكز التشتت من أجل البساطة، إلا أن البلورات الحقيقية عبارة عن هياكل في ثلاثة أبعاد. يمكن أن يحدث التشتت في وقت واحد من مجموعات مختلفة من الطائرات ذات الاتجاهات المختلفة وأنماط المسافات المعروفة باسم طائرات Bragg، كما هو موضح في الشكل\(\PageIndex{3}\). يمكن أن يكون نمط التداخل الناتج معقدًا جدًا.