4.5: حواجز الحيود
- Page ID
- 196539
في نهاية هذا القسم، ستكون قادرًا على:
- ناقش النمط الذي تم الحصول عليه من حواجز الحيود
- شرح تأثيرات محزوز الحيود
يحدد تحليل تداخل الضوء الذي يمر عبر شقين الإطار النظري للتداخل ويعطينا نظرة تاريخية عن تجارب توماس يونغ. ومع ذلك، فإن معظم التطبيقات الحديثة لتداخل الشق لا تستخدم شققين فحسب، بل تستخدم العديد منها، والتي تقترب من اللانهاية لأغراض عملية. يُطلق على العنصر البصري الرئيسي اسم محزوز الحيود، وهو أداة مهمة في التحليل البصري.
حواجز الحيود: عدد لا نهائي من الشقوق
يسمح لنا تحليل التداخل متعدد الشقوق في التداخل بالنظر في ما يحدث عندما يقترب عدد الشقوق N من اللانهاية. تذكر أن الحد الأقصى\(N - 2\) الثانوي يظهر بين الحد الأقصى الرئيسي. يمكننا أن نرى أنه سيكون هناك عدد لا حصر له من الحدود القصوى الثانوية التي تظهر، وعدد لا حصر له من الحواف الداكنة بينهما. هذا يجعل التباعد بين الأطراف، وبالتالي عرض الحد الأقصى، صغيرًا للغاية. علاوة على ذلك، نظرًا لأن شدة الحد الأقصى الثانوي تتناسب مع\(1/N^2\)، فإنها تقترب من الصفر بحيث لا يتم رؤية الحد الأقصى الثانوي. ما تبقى هو الحد الأقصى الرئيسي فقط، وهو الآن مشرق جدًا وضيق جدًا (الشكل\(\PageIndex{1}\)).
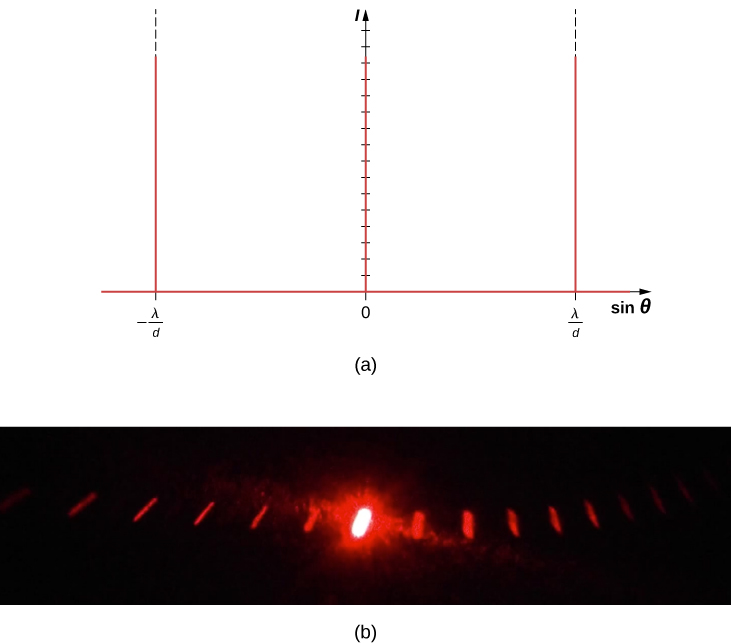
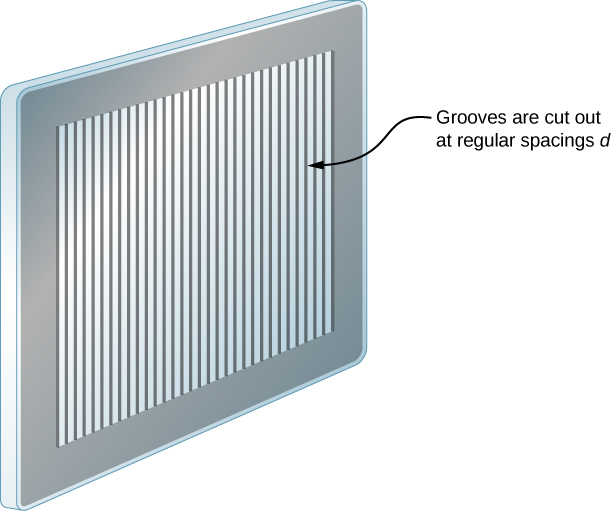
في الواقع، عدد الشقوق ليس بلا حدود، ولكن يمكن أن يكون كبيرًا جدًا - كبيرًا بما يكفي لإنتاج التأثير المكافئ. والمثال الرئيسي هو عنصر بصري يسمى محزوز الحيود. يمكن تصنيع مشبك الحيود عن طريق نحت الزجاج باستخدام أداة حادة في عدد كبير من الخطوط المتوازية الموضوعة بدقة، مع وجود مناطق لم يمسها أحد تعمل مثل الشقوق (الشكل\(\PageIndex{2}\)). يمكن إنتاج هذا النوع من الصريف بكميات كبيرة من خلال التصوير الفوتوغرافي بسعر رخيص. نظرًا لأنه يمكن أن يكون هناك أكثر من 1000 خط في المليمتر عبر المحزوز، عندما يضيء قسم صغير يصل إلى بضعة ملليمترات بواسطة شعاع وارد، يكون عدد الشقوق المضيئة غير محدود فعليًا، مما يوفر الحد الأقصى الأساسي الحاد جدًا.
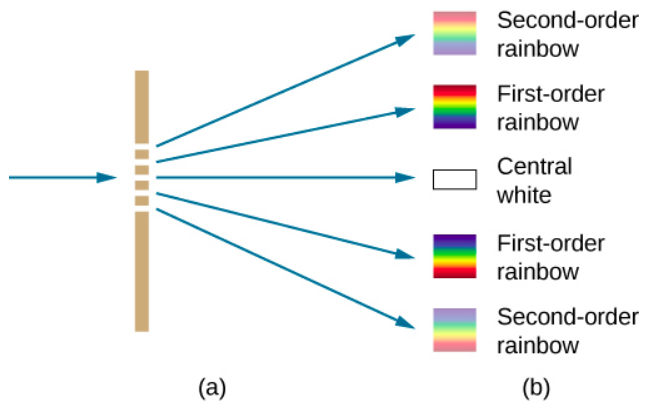
تعمل حواجز الحيود على كل من نقل الضوء، كما في الشكل\(\PageIndex{3}\)، ولانعكاس الضوء، كما هو الحال في أجنحة الفراشة والأوبل الأسترالي في الشكل\(\PageIndex{4a}\). تحدث حواجز الحيود الطبيعية أيضًا في ريش بعض الطيور مثل الطائر الطنان. تعمل الهياكل الصغيرة التي تشبه الأصابع في الأنماط العادية كحواجز شبكية للانعكاس، وتنتج تداخلًا بناءً يمنح الريش ألوانًا ليس فقط بسبب تصبغه. وهذا ما يسمى التقزح اللوني.

تطبيقات حواجز الحيود
أين تستخدم حواجز الحيود في التطبيقات؟ تُستخدم حواجز الحيود بشكل شائع للتشتت الطيفي وتحليل الضوء. ما يجعلها مفيدة بشكل خاص هو حقيقة أنها تشكل نمطًا أكثر حدة من الشقوق المزدوجة. أي أن أطرافها الساطعة أضيق وأكثر إشراقًا بينما تكون مناطقها المظلمة داكنة. حواجز الحيود هي المكونات الرئيسية للمونوكروماتورات المستخدمة، على سبيل المثال، في التصوير البصري لأطوال موجية معينة من العينات البيولوجية أو الطبية. يمكن اختيار محزوز الحيود لتحليل الطول الموجي المنبعث من الجزيئات في الخلايا المريضة في عينة خزعة على وجه التحديد أو للمساعدة في إثارة الجزيئات الإستراتيجية في العينة بطول موجة محددة من الضوء. استخدام حيوي آخر هو في تقنيات الألياف الضوئية حيث تم تصميم الألياف لتوفير الأداء الأمثل بأطوال موجية محددة. تتوفر مجموعة من حواجز الحيود لاختيار الأطوال الموجية لمثل هذا الاستخدام.
تتوفر شبكات الحيود التي تحتوي على 10000 خط لكل سنتيمتر بسهولة. لنفترض أن لديك واحدًا، وأرسلت شعاعًا من الضوء الأبيض عبره إلى شاشة على بعد 2.00 متر.
- أوجد زوايا الحيود من الدرجة الأولى لأقصر وأطول أطوال موجية للضوء المرئي (380 و760 nm، على التوالي).
- ما المسافة بين طرفي قوس قزح للضوء المرئي الناتج على الشاشة للتداخل من الدرجة الأولى؟ (الشكل\(\PageIndex{5}\)).
-
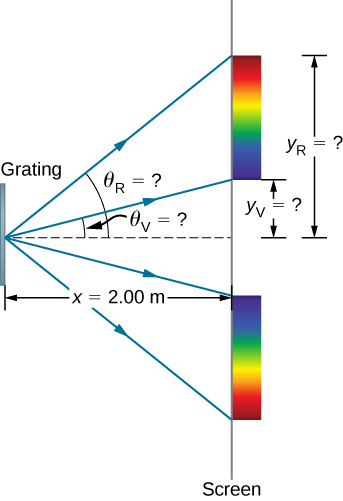
الشكل\(\PageIndex{5}\): (أ) ينتج محزوز الحيود المذكور في هذا المثال قوس قزح من الألوان على الشاشة على مسافة\(x = 2.00 \, m\) من المشبك. يتم قياس المسافات على طول الشاشة بشكل عمودي على الاتجاه x. بمعنى آخر، يمتد نمط قوس قزح خارج الصفحة.
(ب) من منظور عين الطائر، يمكن رؤية نمط قوس قزح على طاولة توضع فيها المعدات.
إستراتيجية
بمجرد تحديد قيمة تباعد\(d\) شق مشبك الحيود، يمكن العثور على زوايا الخطوط الحادة باستخدام المعادلة
\[d \, \sin \, \theta = m\lambda \nonumber \]
من أجل\(m = 0, \pm1, \pm2, ... \).
نظرًا لوجود 10000 سطر في السنتيمتر، يتم فصل كل سطر بمقدار 1/10000 من السنتيمتر. بمجرد معرفة الزوايا، يمكننا إيجاد المسافات على طول الشاشة باستخدام علم المثلثات البسيط.
الحل
- المسافة بين الشقوق هي\(d = (1 \, cm)/10,000 = 1.00 \times 10^{-4} \, cm\) أو\(1.00 \times 10^{-6} m\). دعونا نسمي الزاويتين\(\theta_V\) للبنفسجي (380 نانومتر) والأحمر\(\theta_R\) (760 نانومتر). حل المعادلة\(d \, \sin \theta_V = m\lambda\) لـ\(\sin \, \theta_V\)،
\[\sin \, \theta_V = \frac{m\lambda_V}{d},\nonumber \]
حيث m = 1 للترتيب الأول و\(\lambda_V = 380 \, nm = 3.80 \times 10^{-7}m\). يعطي استبدال هذه القيم\[\sin \, \theta_V = \frac{3.80 \times 10^{-7}m}{1.00 \times 10^{-6}m} = 0.380.\nonumber \]
وبالتالي فإن الزاوية\(\theta_V\) هي\[\theta_V = \sin^{-1} 0.380 = 22.33°.\nonumber \]
وبالمثل،\[\sin \, \theta_R = \frac{7.60 \times 10^{-7}m}{1.00 \times 10^{-6}m} = 0.760.\nonumber \]
وبالتالي فإن الزاوية\(\theta_R\) هي\[\theta_R = \sin^{-1} 0.760 = 49.46°. \nonumber \]
لاحظ أنه في كلتا المعادلتين، أبلغنا عن نتائج هذه الحسابات الوسيطة إلى أربعة أرقام معنوية لاستخدامها في الحساب في الجزء (ب). - يتم تسمية المسافات على الشاشة\(y_V\)\(y_R\) وفي الشكل\(\PageIndex{5}\). لاحظ ذلك\(tan \, \theta = y/x\). يمكننا حل مشكلة\(y_V\) و\(y_R\). وهذا هو،
\[y_V = x \, \tan \, \theta_V = (2.00 \, m)(\tan \, 22.33°) = 0.815 \, m \nonumber \]
و\[y_R = x \, \tan \, \theta_R = (2.00 \, m)(\tan \, 49.46°) = 2.338 \, m. \nonumber \]
وبالتالي فإن المسافة بينهما\[y_R - y_V = 1.523 \, m \nonumber \]
الدلالة
تشير المسافة الكبيرة بين طرفي قوس قزح الأحمر والبنفسجي الناتج من الضوء الأبيض إلى إمكانات صريف الحيود هذا كأداة طيفية. كلما تمكنت من نشر الأطوال الموجية (تشتت أكبر)، يمكن رؤية المزيد من التفاصيل في الطيف. يعتمد هذا على جودة مشبك الحيود - يجب أن يكون دقيقًا جدًا بالإضافة إلى وجود خطوط متباعدة بشكل وثيق.
إذا لم يكن تباعد الأسطر في\(d\) محزوز الحيود معروفًا بدقة، فيمكننا استخدام مصدر ضوء بطول موجة محدد جيدًا لقياسه. لنفترض أن الحافة البنائية من الدرجة الأولى لخط\(H_{\beta}\) انبعاث الهيدروجين (\(\lambda = 656.3 \, nm\)) تقاس عند 11.36 درجة باستخدام مطياف مع محزوز حيود. ما هو تباعد الأسطر في هذا المشبك؟
- إجابة
-
\(3.332 \times 10^{-6} m\)أو 300 خط لكل ملليمتر
خذ نفس المحاكاة التي استخدمناها لحيود الشق المزدوج وحاول زيادة عدد الشقوق من\(N = 2\) إلى\(N = 3, 4, 5, ...\). تصبح القمم الأولية أكثر حدة، وتصبح القمم الثانوية أقل وضوحًا. في الوقت الذي تصل فيه إلى العدد الأقصى\(N = 20\)، يتصرف النظام كثيرًا مثل محزوز الحيود.


