4.4: حيود الشق المزدوج

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• وصف التأثير المشترك للتداخل والانحراف بفتحتين، كل منهما بعرض محدود
• حدد الكثافة النسبية لهامش التداخل ضمن نمط الحيود
• حدد الطلبات المفقودة، إن وجدت

عندما درسنا التداخل في تجربة يونغ ذات الشق المزدوج، تجاهلنا تأثير الحيود في كل شق. لقد افترضنا أن الشقوق كانت ضيقة جدًا لدرجة أنك رأيت على الشاشة فقط تداخل الضوء من مصدرين فقط. إذا كان الشق أصغر من الطول الموجي، فإن الشكل 4.3.4a يوضح أن هناك مجرد انتشار للضوء ولا توجد قمم أو أحواض على الشاشة. لذلك، كان من المعقول استبعاد تأثير الحيود في هذا الفصل. ومع ذلك، إذا قمت بتوسيع الشق، فإن الشكل 4.3.4b و (ج) يوضحان أنه لا يمكنك تجاهل الحيود. في هذا القسم، ندرس مضاعفات تجربة الشق المزدوج التي تنشأ عندما تحتاج أيضًا إلى مراعاة تأثير الحيود لكل شق.

لحساب نمط الحيود لشقين (أو أي عدد من الشقوق)، نحتاج إلى تعميم الطريقة التي استخدمناها للتو لشق واحد. أي أنه عبر كل شق، نضع توزيعًا موحدًا للمصادر النقطية التي تشع موجات Huygens، ثم نجمع الموجات من جميع الشقوق. هذا يعطي الكثافة في أي نقطة على الشاشة. على الرغم من أن تفاصيل هذا الحساب يمكن أن تكون معقدة، إلا أن النتيجة النهائية بسيطة للغاية:

نمط الحيود ثنائي الشق

إن نمط الحيود لشقين عرضيين مفصولين بمسافة d هو نمط التداخل لمصدرين من النقاط يفصل بينهما d مضروبًا في نمط الحيود لشقة العرض$a$.$a$

بمعنى آخر، يتم تحديد مواقع أطراف التداخل من خلال المعادلة

$$d \, \sin \, \theta = m \lambda \nonumber$$

كما هو الحال عندما اعتبرنا الشقوق مصادر نقطية، ولكن شدة الأطراف تقل الآن بتأثيرات الحيود، وفقًا للمعادلة 4.3.11. [لاحظ أنه في الفصل الخاص بالتداخل، كتبنا$d \, sin \, \theta = m \lambda$ واستخدمنا العدد الصحيح للإشارة$m$ إلى هامش التداخل. تستخدم المعادلة 4.2.1 أيضًا$m$، ولكن هذه المرة للإشارة إلى الحد الأدنى للحيود. إذا تم استخدام كلتا المعادلتين في وقت واحد، فمن الممارسات الجيدة استخدام متغير مختلف (مثل$n$) لأحد هذه الأعداد الصحيحة من أجل إبقائها مميزة.]

تعمل تأثيرات التداخل والانحراج في وقت واحد وتنتج عمومًا الحد الأدنى بزوايا مختلفة. يؤدي هذا إلى ظهور نمط معقد على الشاشة، حيث تكون بعض الحدود القصوى للتداخل من الشقين مفقودة إذا كان الحد الأقصى للتداخل في نفس اتجاه الحد الأدنى من الحيود. نشير إلى مثل هذه الذروة المفقودة على أنها طلب مفقود. يوضح الشكل أحد أمثلة نمط الحيود على الشاشة$\PageIndex{1}$. الخط الصلب ذو القمم المتعددة بارتفاعات مختلفة هو الكثافة الملاحظة على الشاشة. إنه نتاج نمط تداخل الموجات من الشقوق المنفصلة وانحراف الموجات من داخل شق واحد.

الشكل$\PageIndex{1}$: الانحراف عن الشق المزدوج. يأتي الخط الأرجواني ذو القمم التي لها نفس الارتفاع من تداخل الموجات من شقين؛ والخط الأزرق ذو الحدبة الكبيرة في المنتصف هو انحراف الموجات من داخل شق واحد؛ والخط الأحمر السميك هو نتاج الشقين، وهو النمط الذي لوحظ على الشاشة. يُظهر الرسم النتيجة المتوقعة لعرض الشق$a = 2\lambda$ وفصل الشق$d = 6\lambda$. الحد الأقصى$m = \pm 3$ لترتيب التداخل مفقود لأن الحد الأدنى من الحيود يحدث في نفس الاتجاه.

مثال$\PageIndex{1}$: Intensity of the Fringes

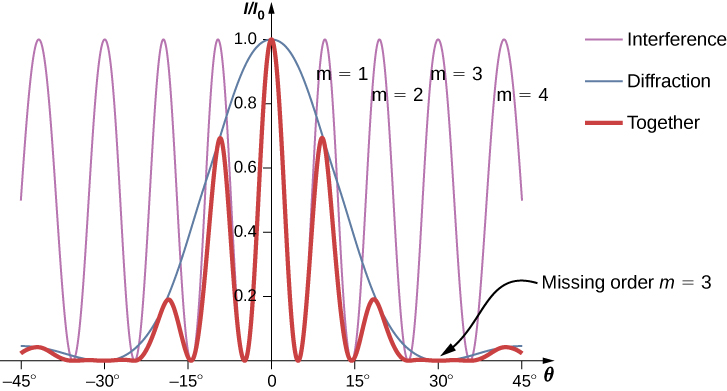
$\PageIndex{1}$يوضح الشكل أن شدة الحافة لـ m=3 تساوي صفرًا، ولكن ماذا عن الأطراف الأخرى؟ احسب شدة الحافة عند m=1 بالنسبة$I_0$ لشدة الذروة المركزية.

إستراتيجية

أوجد زاوية هامش التداخل ذي الشق المزدوج باستخدام المعادلة من التداخل، ثم حدِّد الكثافة النسبية في هذا الاتجاه بسبب الحيود باستخدام المعادلة 4.3.11.

الحل

من الفصل الخاص بالتداخل، نعلم أن أطراف التداخل الساطعة تحدث عند$d \, sin \, \theta = m \lambda$ أو

$$\sin \, \theta = \dfrac{m\lambda}{d}. \nonumber$$

من المعادلة 4.3.11،

$$I = I_0 \left(\dfrac{\sin \, \beta}{\beta}\right)^2 \nonumber$$

حيث

$$\beta = \dfrac{\phi}{2} = \dfrac{\pi a \sin \, \theta}{\lambda}. \nonumber$$

والاستعاضة عن ذلك من فوق،

$$\beta = \dfrac{\pi a \sin \, \theta}{\lambda} = \dfrac{\pi a}{\lambda} \cdot \dfrac{m\lambda}{d} = \dfrac{m\pi a}{d}. \nonumber$$

من أجل$a = 2\lambda, \, d = 6 \lambda$، و$m = 1$،

$$\beta = \dfrac{(1)\pi (2\lambda)}{(6 \lambda)} = \dfrac{\pi}{3}. \nonumber$$

ثم الكثافة هي

$$I = I_0 \left(\dfrac{\sin \, \beta}{\beta}\right)^2 = I_0 \left(\dfrac{sin \, (\pi/3)}{\pi/3}\right)^2 = 0.684 I_0. \nonumber$$

الدلالة

لاحظ أن هذا الأسلوب بسيط نسبيًا ويعطي نتيجة تشبه تقريبًا التحليل الأكثر تعقيدًا باستخدام أجهزة الطور لحساب قيم شدة التداخل المزدوج (الخط الرقيق في الشكل$\PageIndex{1}$). يمثل نهج الطور المنحدر الهابط في شدة الحيود (الخط الأزرق) بحيث تحدث الذروة بالقرب من m=1 عند قيمة أصغر قليلاً مما أظهرناه هنا.

مثال$\PageIndex{2}$: Two-Slit Diffraction

لنفترض أنه في تجربة يونغ، يتم فصل الشقوق التي يبلغ عرضها 0.020 مم بمقدار 0.20 مم. إذا كانت الشقوق مضاءة بضوء أحادي اللون طوله الموجي ٥٠٠ نانومترًا، فما عدد الأطراف الساطعة التي تُلاحظ في الذروة المركزية لنمط الحيود؟

الحل

من المعادلة 4.2.1، يكون الموضع الزاوي لأدنى الحيود الأول هو$\theta \approx sin \, \theta = \dfrac{\lambda}{a} = \dfrac{5.0 \times 10^{-7}m}{2.0 \times 10^{-5}m} = 2.5 \times 10^{-2} rad$.

باستخدام$d \sin \, \theta = m \lambda$$\theta = 2.5 \times 10^{-2} rad$ FOR، نجد

$$m = \dfrac{d \, sin \, \theta}{\lambda} = \dfrac{(0.20 \, mm)(2.5 \times 10^{-2} rad)}{(5.0 \times 10^{-7}m)} = 10, \nonumber$$

وهو الحد الأقصى لترتيب التداخل الذي يتناسب مع الذروة المركزية. نلاحظ أن الطلبات$m=±10$ تفتقد إلى$θ$ المطابقات تمامًا. وفقًا لذلك، نلاحظ وجود هامش مشرق لـ

م = −9، −8، −7، −6، −5، −4، −3، −2، −1، 0، +1، +2، +3، +4، +5، +6، +7، +8، +9

ليصبح المجموع 19 شريطًا مشرقًا.

التمارين$\PageIndex{1}$

بالنسبة للتجربة في المثال$\PageIndex{2}$، أظهر أن m=20 هو أيضًا ترتيب مفقود.

الحل

من$d \, \sin \, \theta = m\lambda$، يحدث الحد الأقصى للتداخل عند$2.87^o$ النقطة$m = 20$. من المعادلة 4.2.1، هذه هي أيضًا زاوية الحد الأدنى للحيود الثاني. (ملاحظة: تستخدم كلتا المعادلتين الفهرس m ولكنهما يشيران إلى ظواهر منفصلة.)

استكشف تأثيرات حيود الشق المزدوج. في هذه المحاكاة التي كتبها Fu-Kwun Hwang، حدد N=2 باستخدام شريط التمرير وشاهد ما يحدث عندما تتحكم في عرض الشق وفصل الشق والطول الموجي. هل يمكنك جعل الطلب «مفقودًا»؟